The results of the Olympics on programming among schoolchildren
From January 16 to January 22 at the Moscow University of Steel and Alloys the III International School Olympiad in programming was held. The event was organized by NUST “MISiS” and Cognitive Technologies. Frankly speaking, it took almost three weeks to persuade the organizers to open at least a couple of conditions of the tasks proposed at the event and to get permission to publish their analysis.
Believe me, it was not easy. Although they can be understood.
As you know, the preparation of the conditions of tasks is considered one of the most difficult stages in the preparation of programming competitions.
Upon completion, they are usually used in training teams, as well as external contests.
Teams of trainers from different universities regularly exchange contests.
In general, reuse of tasks is accepted in the olympiad movement.

But first things first.
More than 70 schoolchildren from grades 8 to 11 from different regions of Russia and the Republic of Belarus who successfully performed in the correspondence round of the Olympiad were invited to participate in the full-time round of the Olympiad.
Recall that the format of the event involves two stages: correspondence (held in the fall; last year it took place on November 16, 2014; more details about it can be found at: http://ug.ru/news/13584 ) and full-time (held in early January) .
The organizers note that they do not rely on geniuses and geeks from special schools in Moscow and St. Petersburg.
The aim of the Olympiad is to search for promising and talented guys, mainly from the regions of Russia and neighboring countries, who want to get a good education and realize themselves in the field of information technology.
Starting from the 2nd year of study, students of the Department of Engineering Cybernetics practice at university laboratories and the best of them are invited to take part in real scientific and applied projects in the field of AI implemented jointly with Cognitive Technologies.
The full-time round of the Olympiad was held according to the following rules.
When ranking participants and identifying winners, the main factor was the number of tasks solved.
When they were equal, the sum of the times from the start of the tournament to the adoption by the checking system of a decision on all the problems solved plus 20 minutes of a penalty for each rejected decision was taken into account.
Penalties for incorrect decisions were imposed only on those tasks that were ultimately accepted by the verification system.
For automated decision verification, the ejudge system was used ( https://ejudge.ru/ ).
As a result, nobody solved 10 problems.
The winner of the Olympiad was the silver medalist at the International Olympiad in Informatics Alexey Vistyazhfrom Iviev Secondary School of the Republic of Belarus, which solved 9 problems.
With a noticeable margin from him (5 solved problems), Alexander Zoykin (Orenburg) and Yuri Bondarchuk (Belarus) shared the second place . Pavel Beschetnov (Tolyati), Dmitry Galov (Moscow) and Aleksey Dovgal (Belarus)
were in third place with four tasks solved . 16 schoolchildren, recognized as winners and prize-winners, received valuable prizes and additional points to the overall results of the exam on admission to the NUST “MISiS”. The greatest difficulty was caused by task I. “Mirror in the corridor”. Surprisingly, the participants did poorly with geometry problems.
The organizers considered them relatively simple.
Time limit: 0.5 second
Memory limit: 64 megabytes
Input: Standard input stream (stdin)
Output: Standard output stream (stdout)
Cold Petya was lying in bed when someone opened the door. Petya was too lazy to get up and he looked in the mirror to see who had come. The coordinates of the person entering are known (it can be considered a material point), it is necessary to find out if Pete will be able to see the reflection of the person entering in the mirror. The mirror has the shape of a circle centered at the origin and is located in the plane ax + by + cz= 0. Petya can also be considered a material point. It is guaranteed that Petya and the stranger do not lie in the plane of the mirror and that Petya always sees the reflecting side of the mirror. If the image hits the border of the mirror, then Petya sees the person entering. Since both Petya and the person entering can be considered material points, Petya can see the reflection of the person entering both through the person entering and through his own reflection.
The first line contains a positive integer n - the number of tests not exceeding 500. Each test consists of four lines. The first of them contains the radius of the mirror. In the second, the coefficients a , b , c . Followed by the coordinates of Petit. The fourth line of each test contains the coordinates of the person who entered. All numbers are integers and do not exceed 1000 in absolute value.
Print n lines. On each line is the answer to the next test. “Yes” if Petya sees the person coming in and “No” otherwise.
Reflect Petya relative to the plane of the mirror.
Draw a straight line through the reflected Petya and the stranger and cross it with the plane of the mirror. Let's see if the intersection point hits the mirror. We will separately consider the case when Petya and a stranger are lying on opposite sides of the mirror - then Petya definitely does not see him.

The text of the problem H "The axis of symmetry"
Time limit: 1 second
Memory limit: 64 Megabytes
Input: Standard input stream (stdin)
Output: Standard output stream (stdout)
Friends brought a gift for a kite from a trip to China.
The next day the weather was fine, and he decided to glue the snake and run it.
The manufacturing instructions, of course, were only in Chinese, so Vova decided that he would figure it out without it.
Having tinkered a bit, he built a snake in the shape of a flat polygon, all that remained was to stick a tail to it.
And then Vova had to think about what point the snake’s tail should be glued to.
Intuition told him that in order for the flight of the snake to be stable, its tail should lie on some axis of symmetry of the polygon.
The figures below show two kites flying stably and all the options for attaching a tail to them,
as well as one kite flying unstable.
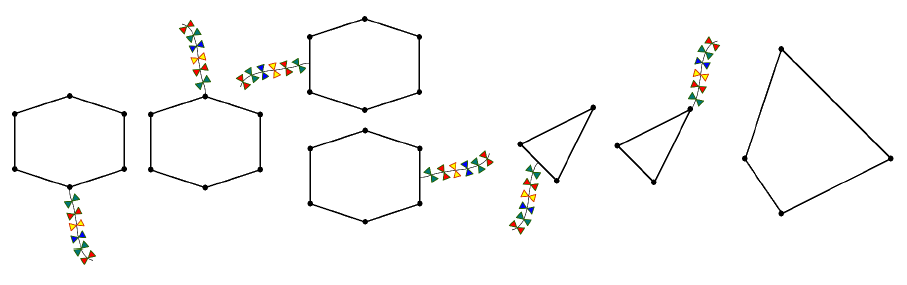
How many points exist on the border of the polygon, such that if you stick the tail to them, the result is a kite flying stably?
Initial data
The first line contains a single integer N (3 ≤ N ≤ 1000). The next N lines contain two space-separated integers that do not exceed 10,000 in absolute value - the coordinates of the vertices of the polygon in the traversal order.
Result
Print a single number - the number of points on the border of the polygon to which you can stick the tail of the snake.
The axis of symmetry of a polygon can pass only through its vertices and through the midpoints of its sides.
We write down the coordinates of 2N points - the vertices of the polygon and the midpoints of its sides in the traversal order and number them from 0 to 2N-1 .
Consider all the contenders for the axis of symmetry - the lines passing through the points i and i + N, 0 ≤ i ≤ N -1.
In order for such a line to be the axis of symmetry of the polygon, it is necessary and sufficient that each pair of points i + j and (ij) mod 2N, 1 ≤ j ≤ N-1, be located symmetrically with respect to this line.
Check the symmetry of the location of points Cand D with respect to the straight line AB is easiest, having established that the lines AB and CD are orthogonal and their intersection point divides the segment CD in half.
In order not to go beyond the calculation with integers, it is enough to increase all the coordinates of the points by 4 times.
The complexity of such a solution is O (N 2 ).
Two participants A. Vistyazh and P. Beschetnov coped with task H “The axis of symmetry” .
During the full-time tour, a winter programming school was also held for the children.
Within its framework, well-known scientists and IT specialists delivered lectures to the participants of the Olympiad, held master classes and educational contests.
Participation in the winter school and in-person round of the programming Olympiad was free for invited participants. They were provided with transfers, meals and accommodation.
Each participant was met at the station and escorted to the venue. Throughout the stay, professional counselors worked with schoolchildren, trained at the counselor school organized by the travel company OST-WEST.
Tasks and tests for the full-time round of the Olympiad were developed by a team of trainers in sports programming of NUST “MISiS” and Cognitive Technologies led by a corresponding member. RAS V.L. Arlazarov. Among them: Ph.D. I.A. Farajev, Ph.D. V.V. Postnikov, Ph.D. I.B. Mamai, V.V. Sokolov. And also graduate students of NUST “MISiS”: K. Bulatov, T. Chernov and N. Skoryukina.
Believe me, it was not easy. Although they can be understood.
As you know, the preparation of the conditions of tasks is considered one of the most difficult stages in the preparation of programming competitions.
Upon completion, they are usually used in training teams, as well as external contests.
Teams of trainers from different universities regularly exchange contests.
In general, reuse of tasks is accepted in the olympiad movement.

But first things first.
More than 70 schoolchildren from grades 8 to 11 from different regions of Russia and the Republic of Belarus who successfully performed in the correspondence round of the Olympiad were invited to participate in the full-time round of the Olympiad.
Recall that the format of the event involves two stages: correspondence (held in the fall; last year it took place on November 16, 2014; more details about it can be found at: http://ug.ru/news/13584 ) and full-time (held in early January) .
The organizers note that they do not rely on geniuses and geeks from special schools in Moscow and St. Petersburg.
The aim of the Olympiad is to search for promising and talented guys, mainly from the regions of Russia and neighboring countries, who want to get a good education and realize themselves in the field of information technology.
Starting from the 2nd year of study, students of the Department of Engineering Cybernetics practice at university laboratories and the best of them are invited to take part in real scientific and applied projects in the field of AI implemented jointly with Cognitive Technologies.
The full-time round of the Olympiad was held according to the following rules.
- Duration of the tour: 5 hours .
- Number of tasks: 10 .
- Working language: Russian .
When ranking participants and identifying winners, the main factor was the number of tasks solved.
When they were equal, the sum of the times from the start of the tournament to the adoption by the checking system of a decision on all the problems solved plus 20 minutes of a penalty for each rejected decision was taken into account.
Penalties for incorrect decisions were imposed only on those tasks that were ultimately accepted by the verification system.
For automated decision verification, the ejudge system was used ( https://ejudge.ru/ ).
As a result, nobody solved 10 problems.
The winner of the Olympiad was the silver medalist at the International Olympiad in Informatics Alexey Vistyazhfrom Iviev Secondary School of the Republic of Belarus, which solved 9 problems.
With a noticeable margin from him (5 solved problems), Alexander Zoykin (Orenburg) and Yuri Bondarchuk (Belarus) shared the second place . Pavel Beschetnov (Tolyati), Dmitry Galov (Moscow) and Aleksey Dovgal (Belarus)
were in third place with four tasks solved . 16 schoolchildren, recognized as winners and prize-winners, received valuable prizes and additional points to the overall results of the exam on admission to the NUST “MISiS”. The greatest difficulty was caused by task I. “Mirror in the corridor”. Surprisingly, the participants did poorly with geometry problems.
The organizers considered them relatively simple.
Task I text
Time limit: 0.5 second
Memory limit: 64 megabytes
Input: Standard input stream (stdin)
Output: Standard output stream (stdout)
Cold Petya was lying in bed when someone opened the door. Petya was too lazy to get up and he looked in the mirror to see who had come. The coordinates of the person entering are known (it can be considered a material point), it is necessary to find out if Pete will be able to see the reflection of the person entering in the mirror. The mirror has the shape of a circle centered at the origin and is located in the plane ax + by + cz= 0. Petya can also be considered a material point. It is guaranteed that Petya and the stranger do not lie in the plane of the mirror and that Petya always sees the reflecting side of the mirror. If the image hits the border of the mirror, then Petya sees the person entering. Since both Petya and the person entering can be considered material points, Petya can see the reflection of the person entering both through the person entering and through his own reflection.
Initial data
The first line contains a positive integer n - the number of tests not exceeding 500. Each test consists of four lines. The first of them contains the radius of the mirror. In the second, the coefficients a , b , c . Followed by the coordinates of Petit. The fourth line of each test contains the coordinates of the person who entered. All numbers are integers and do not exceed 1000 in absolute value.
Result
Print n lines. On each line is the answer to the next test. “Yes” if Petya sees the person coming in and “No” otherwise.
Example
| Initial data | Result |
|---|---|
| 2 2 0 1 0 0 2 0 0 1 0 1 0 1 0 2 -2 0 0 1 1 0 | Yes no |
Analysis of task I “Mirror in the corridor”
Reflect Petya relative to the plane of the mirror.
Draw a straight line through the reflected Petya and the stranger and cross it with the plane of the mirror. Let's see if the intersection point hits the mirror. We will separately consider the case when Petya and a stranger are lying on opposite sides of the mirror - then Petya definitely does not see him.

The text of the problem H "The axis of symmetry"
Time limit: 1 second
Memory limit: 64 Megabytes
Input: Standard input stream (stdin)
Output: Standard output stream (stdout)
Friends brought a gift for a kite from a trip to China.
The next day the weather was fine, and he decided to glue the snake and run it.
The manufacturing instructions, of course, were only in Chinese, so Vova decided that he would figure it out without it.
Having tinkered a bit, he built a snake in the shape of a flat polygon, all that remained was to stick a tail to it.
And then Vova had to think about what point the snake’s tail should be glued to.
Intuition told him that in order for the flight of the snake to be stable, its tail should lie on some axis of symmetry of the polygon.
The figures below show two kites flying stably and all the options for attaching a tail to them,
as well as one kite flying unstable.

How many points exist on the border of the polygon, such that if you stick the tail to them, the result is a kite flying stably?
Initial data
The first line contains a single integer N (3 ≤ N ≤ 1000). The next N lines contain two space-separated integers that do not exceed 10,000 in absolute value - the coordinates of the vertices of the polygon in the traversal order.
Result
Print a single number - the number of points on the border of the polygon to which you can stick the tail of the snake.
Example
| Initial data | Result |
|---|---|
| 6 3 3 6 2 6 -1 3 -2 0 -1 0 2 | 4 |
| 3 -2 2 2 4 0 0 | 2 |
| 4 0 6 6 0 0 -3 -2 0 | 0 |
Analysis of Problem H “Axis of Symmetry”
The axis of symmetry of a polygon can pass only through its vertices and through the midpoints of its sides.
We write down the coordinates of 2N points - the vertices of the polygon and the midpoints of its sides in the traversal order and number them from 0 to 2N-1 .
Consider all the contenders for the axis of symmetry - the lines passing through the points i and i + N, 0 ≤ i ≤ N -1.
In order for such a line to be the axis of symmetry of the polygon, it is necessary and sufficient that each pair of points i + j and (ij) mod 2N, 1 ≤ j ≤ N-1, be located symmetrically with respect to this line.
Check the symmetry of the location of points Cand D with respect to the straight line AB is easiest, having established that the lines AB and CD are orthogonal and their intersection point divides the segment CD in half.
In order not to go beyond the calculation with integers, it is enough to increase all the coordinates of the points by 4 times.
The complexity of such a solution is O (N 2 ).
Two participants A. Vistyazh and P. Beschetnov coped with task H “The axis of symmetry” .
Winter school
During the full-time tour, a winter programming school was also held for the children.
Within its framework, well-known scientists and IT specialists delivered lectures to the participants of the Olympiad, held master classes and educational contests.
Participation in the winter school and in-person round of the programming Olympiad was free for invited participants. They were provided with transfers, meals and accommodation.
Each participant was met at the station and escorted to the venue. Throughout the stay, professional counselors worked with schoolchildren, trained at the counselor school organized by the travel company OST-WEST.
Tasks and tests for the full-time round of the Olympiad were developed by a team of trainers in sports programming of NUST “MISiS” and Cognitive Technologies led by a corresponding member. RAS V.L. Arlazarov. Among them: Ph.D. I.A. Farajev, Ph.D. V.V. Postnikov, Ph.D. I.B. Mamai, V.V. Sokolov. And also graduate students of NUST “MISiS”: K. Bulatov, T. Chernov and N. Skoryukina.
