Non-recursive permutation generation algorithm
The non-recursive algorithm proposed below differs somewhat from those described in Lipsky’s book [1] and discovered by me in the Russian-language segment of the Internet. I hope it will be interesting.
Brief statement of the problem. There is a set of dimension N. It is necessary to obtain all N! possible permutations.
Further, for simplicity, we use integers (1..N) as a set. Instead of numbers, you can use any objects, because there are no operations to compare elements of the set in the algorithm.
To store the intermediate data, we will form a data structure of the following form:
and fill it with the original values
The number of the element in the masiv array will be called the level.
In the list of the first level we enter all the elements of the set. At the first level, the dimension of the list is N and the list itself does not change throughout the execution of the algorithm. During initial filling, all pointers in the array are set to the first element in the list.
At each next level, its list is formed on the basis of the list of the previous level, but without one element that is marked with a pointer. At the penultimate level (N-2), the list contains three items. At the last level (N-1), the list contains two items. The list of the lower level is formed as a list of the previous level without the element indicated by the pointer of the previous level.
As a result of the initial filling, the first two permutations were obtained. This is a general array formed at the upper levels (1 ... (N-2)) from the list items pointed to by pointers.
and from the list of the last level, two pairs of elements in a different order (two tails 1 2 and 2 1)
All further permutations are also formed, always from the penultimate level (N-2).
The procedure for obtaining subsequent permutations is that, being at the penultimate level (N-2) and having formed two permutations, we try to increase the pointer of the selected element by 1.
If possible, then at the last level we change the list and repeat.
If at the penultimate level it is not possible to increase the pointer (all possible options have been enumerated), then we rise to the level at which increasing the pointer (moving to the right) is possible. The condition for the algorithm to end is that the pointer at the first level goes beyond N.
After moving the pointer to the right, we change the list below it and move down to the penultimate level (N-2), also updating the lists and setting the pointers of the selected item to 1.
The operation of the algorithm is presented more clearly and clearly in the figure below (for the dimension of the set N = 5). The number in the figure corresponds to the level in the description. It is even possible that in addition to the figure, nothing is needed to understand the algorithm.
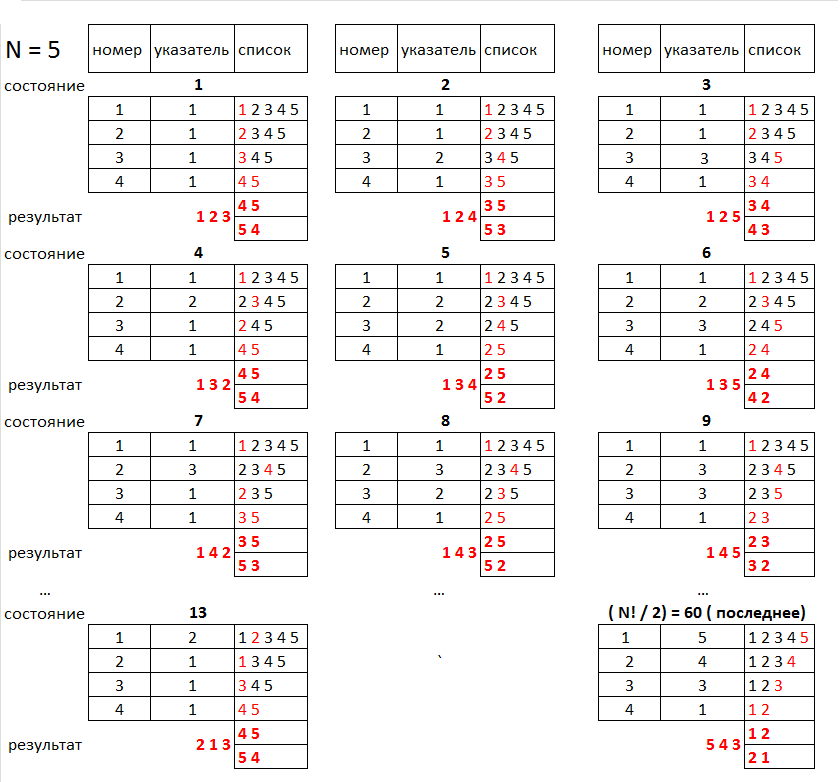
Of course, when implementing the algorithm, it was possible to use the usual two-dimensional array, especially since for small N the gain in memory does not give anything, and for large N we can not wait for the algorithm to finish working.
One way to implement the algorithm on VBA is below. To run it, you can create an Excel workbook with macros, create a module on the VB developer tab, and copy the text to the module. After running generate (), all permutations will be displayed on Sheet1.
References:
[1] V. Lipsky. Combinatorics for programmers. -Moscow, Mir Publishing House, 1988.
Brief statement of the problem. There is a set of dimension N. It is necessary to obtain all N! possible permutations.
Further, for simplicity, we use integers (1..N) as a set. Instead of numbers, you can use any objects, because there are no operations to compare elements of the set in the algorithm.
To store the intermediate data, we will form a data structure of the following form:
type dtree
ukaz as integer ' номер выбранного элемента в списке
spisok() as integer ' список доступных значений
end type
and fill it with the original values
Dim masiv(N-) As dtree ' размерность массива = N-1
For ii = 1 To N - 1
masiv(ii).ukaz = 1
ReDim masiv(ii).spisok(N + 1 - ii) ' устанавливаем размерность списка
For kk = 1 To (N + 1 - ii)
masiv(ii).spisok(kk) = kk + ii - 1
Next
Next
The number of the element in the masiv array will be called the level.
In the list of the first level we enter all the elements of the set. At the first level, the dimension of the list is N and the list itself does not change throughout the execution of the algorithm. During initial filling, all pointers in the array are set to the first element in the list.
At each next level, its list is formed on the basis of the list of the previous level, but without one element that is marked with a pointer. At the penultimate level (N-2), the list contains three items. At the last level (N-1), the list contains two items. The list of the lower level is formed as a list of the previous level without the element indicated by the pointer of the previous level.
As a result of the initial filling, the first two permutations were obtained. This is a general array formed at the upper levels (1 ... (N-2)) from the list items pointed to by pointers.
For ii = 1 To N-2
massiv(ii).spisok(ukaz)
Next
and from the list of the last level, two pairs of elements in a different order (two tails 1 2 and 2 1)
+ massiv(N-1).spisok(1) + massiv(N-1).spisok(2)
+ massiv(N-1).spisok(2) + massiv(N-1).spisok(1)
All further permutations are also formed, always from the penultimate level (N-2).
The procedure for obtaining subsequent permutations is that, being at the penultimate level (N-2) and having formed two permutations, we try to increase the pointer of the selected element by 1.
If possible, then at the last level we change the list and repeat.
If at the penultimate level it is not possible to increase the pointer (all possible options have been enumerated), then we rise to the level at which increasing the pointer (moving to the right) is possible. The condition for the algorithm to end is that the pointer at the first level goes beyond N.
After moving the pointer to the right, we change the list below it and move down to the penultimate level (N-2), also updating the lists and setting the pointers of the selected item to 1.
The operation of the algorithm is presented more clearly and clearly in the figure below (for the dimension of the set N = 5). The number in the figure corresponds to the level in the description. It is even possible that in addition to the figure, nothing is needed to understand the algorithm.

Of course, when implementing the algorithm, it was possible to use the usual two-dimensional array, especially since for small N the gain in memory does not give anything, and for large N we can not wait for the algorithm to finish working.
One way to implement the algorithm on VBA is below. To run it, you can create an Excel workbook with macros, create a module on the VB developer tab, and copy the text to the module. After running generate (), all permutations will be displayed on Sheet1.
VBA for Excel
Option Explicit
Type dtree
tek_elem_ukaz As Integer
spisok() As Integer
End Type
Dim masiv() As dtree
Dim start_print As Integer
Dim N As Integer
Sub generate()
Dim ii As Integer, kk As Integer, jj As Integer
Dim uroven As Integer
Лист1.Cells.Clear
N = 5
start_print = 1
ReDim masiv(N - 1)
' первичное заполнение
For ii = 1 To N - 1
masiv(ii).tek_elem_ukaz = 1
ReDim masiv(ii).spisok(N + 1 - ii)
For kk = 1 To (N + 1 - ii)
masiv(ii).spisok(kk) = kk + ii - 1
Next
Next
uroven = N - 2
Do
' результат
Call print_rezult(uroven)
' на последнем уровне можно сдвинуться вправо
If masiv(uroven).tek_elem_ukaz <= (N - uroven) Then
' делаем шаг вправо
' меняем тек элемент
masiv(uroven).tek_elem_ukaz = masiv(uroven).tek_elem_ukaz + 1
' меняем массив снизу
Call zap_niz(uroven)
Else
' делаем шаг вверх до первого уровня, где можно сдвинуться вправо
Do While uroven > 1 And masiv(uroven).tek_elem_ukaz > (N - uroven)
uroven = uroven - 1
Loop
If uroven = 1 And masiv(1).tek_elem_ukaz = N Then
MsgBox "stop calc"
Exit Sub ' напечатали все
End If
' делаем шаг вправо на первом снизу доступном уровне
masiv(uroven).tek_elem_ukaz = masiv(uroven).tek_elem_ukaz + 1
Call zap_niz(uroven)
' заполнение нижних уровней
Do While uroven < N - 2
uroven = uroven + 1
masiv(uroven + 1).tek_elem_ukaz = 1
' меняем массив снизу
For kk = 2 To N - uroven + 1
masiv(uroven + 1).spisok(kk - 1) = masiv(uroven).spisok(kk)
Next
Loop
End If
Loop
End Sub
Sub print_rezult(ukaz As Integer)
Dim ii As Integer
For ii = 1 To ukaz
With masiv(ii)
Лист1.Cells(start_print, ii) = .spisok(.tek_elem_ukaz)
Лист1.Cells(start_print + 1, ii) = .spisok(.tek_elem_ukaz)
End With
Next
With masiv(ukaz + 1)
Лист1.Cells(start_print, ukaz + 1) = .spisok(1)
Лист1.Cells(start_print, ukaz + 2) = .spisok(2)
start_print = start_print + 1
Лист1.Cells(start_print, ukaz + 1) = .spisok(2)
Лист1.Cells(start_print, ukaz + 2) = .spisok(1)
start_print = start_print + 1
End With
End Sub
Sub zap_niz(ukaz As Integer)
' заполнение нижнего уровня
Dim ii As Integer, wsp1 As Integer
' меняем тек элемент
wsp1 = masiv(ukaz).tek_elem_ukaz
masiv(ukaz + 1).tek_elem_ukaz = 1
' меняем массив снизу
For ii = 1 To wsp1 - 1
masiv(ukaz + 1).spisok(ii) = masiv(ukaz).spisok(ii)
Next
For ii = wsp1 + 1 To N - ukaz + 1
masiv(ukaz + 1).spisok(ii - 1) = masiv(ukaz).spisok(ii)
Next
End Sub
References:
[1] V. Lipsky. Combinatorics for programmers. -Moscow, Mir Publishing House, 1988.
