Mathematica 10 released with 700+ new features and an incredible amount of R&D

Translation of Steven Wolfram's article on the Wolfram Mathematica 10 system, which was released on July 9, 2014.
You can find the original text here .
I express my deep gratitude to those who helped me translate this article: Vladislav Glagolev ( Himura ), Sylvia Torosyan and Rukk Natalia Samuilovna .

This summer we are releasing a truly huge range of new technologies. Two weeks ago, we launched the Wolfram Programming Cloud . And today, I am pleased to present you a largely updated version of Mathematica : Mathematica 10 . We released Mathematica 1



just over 26 years ago, June 23, 1988. Since then, we have constantly and systematically made Mathematica even bigger, more powerful, wider, and deeper. But Mathematica 10, released today, is perhaps the biggest leap in functionality in the entire history of Mathematica .

Personally, I am very pleased after so many years to see how successfully the principles that I identified at the very beginning of the development of Mathematica have shown themselves . It’s also very nice to see how far we have come thanks to our talented collaborators and the hard work of developing Mathematica for almost three decades now.

We probably will never be able to find out if our dedication to R&D (R&D) has been purely commercial in so many years. But it always made sense to me - and the success of Mathematica , like our entire company, allows us to make plans for the distant future, continuously investing in building the most powerful technology layer by layer.

One of our latest projects, the creation of the Wolfram Language , comes from a combination of Mathematica , Wolfram | Alpha, and other technologies. As a result, Mathematica has now become the main application based on the Wolfram Language.

But mathematicastill, to a large extent, retained its individuality, as our oldest flagship product, as well as a system that has been continuously changing the idea of ​​technical computing for almost a quarter of a century.

And today in Mathematica 10 you can see more new functionality than in any of the previous versions of Mathematica . It's nice to see such a long curve of the ever-accelerating development process and realize that in Mathematica 10 more functions were added than there were in the whole of Mathematica 1. So what are the new functionalities of Mathematica 10? This is a mixture of completely new areas and directions (for example, this is -



geometrical computing , machine learning, and geographic computing ) - along with extensive amplification and expansion of existing areas . As well as a mixture of all kinds of objects that I had planned for a long time for our company to solve, but the implementation of which required the development of appropriate technologies by us, together with those objects whose understanding of the possibility of our company came to me only recently. When you start Mathematica 10 for the first time, there are some things you will notice right away. Firstly, Mathematica 10 immediately establishes a connection directly to the Wolfram Cloud (Wolfram Cloud). Unlike



Wolfram Programming Cloud - or the upcoming Mathematica Online ( Mathematica Online) - Mathematica 10 does not launch its interface or computing in the cloud. Instead, it supports all the benefits of running directly on your local computer - but it connects to the Wolfram Cloud (Wolfram Cloud), so it can have files stored in the cloud, work with the cloud API and other cloud features, and it also has access to Cloud-based parts of Wolfram Knowledgebase .

If you are an “active” user of Mathematica , then you will notice some changes at the beginning of working with a document (laptop)Mathematica 10. Now everywhere there is an autocompletion of the entered commands - for values ​​of options of functions, lines - everywhere. There is also a pop-up help menu that immediately displays function templates or documentation for them. There is also - at the request of the user community - the ability to repeatedly cancel actions (Undo). It is extremely difficult to determine how and when the correct cancellation of calculations and other actions in Mathematica is permissible , however, in Mathematica 10 this problem - the repeated cancellation of actions - is solved.

Another notable change in Mathematica 10 is that charts and graphs have, by default, a new, improved view (of course, you can return to the previous view using the appropriate value of the PlotTheme option ). And for many other areas, this is just the tip of the iceberg. In the invisible part of the iceberg there is a new very powerful mechanism for changing “graphic themes” - when instead of many separate options you only need to define a common theme for the chart, for example, “web” (web), “minimal” (minimal) or “scientific” (scientific ) What about algorithms? In Mathematica 10 a tremendous amount of new algorithms. Many new algorithms, many of which we have developed for internal use. For example, an algorithm that allows Mathematica







10 in the usual mode, solve systems of polynomial equations with numerical coefficients having more than 100,000 solutions . Or a cluster of algorithms that was first developed by us, which gives exact symbolic solutions for all types of hybrid differential equations or delay differential equations , turning such equations into standard, ordinary differential equations .



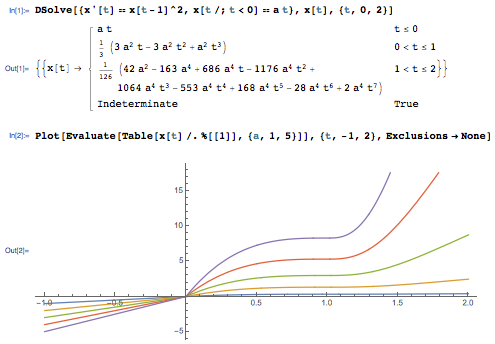
Of course, during the development of algorithms, we are in high spirits. Because our long-term contribution to the design of coherent systems now means that when developing any algorithm, we can easily combine the algorithmic capabilities of the entire system. If, for example, we develop a numerical algorithm, then we can easily create complex algebraic preliminary calculations for this or apply graph theory, or combinatorial optimization, or something like that. And we can create new types of algorithms that combine all their types, as well as approaches, in ways that were previously impossible.

From the very beginning, one of our basic principles was to automate everything as much as possible - and create not just algorithms, but complete meta-algorithms that automate the entire process of transition from the “goal of computing” to how and by which algorithm will be performed computing to achieve this. We have developed a method for such automation, which over the years has allowed us to “absorb” more and more areas of computing, while making them available not only to experts, but also to everyone in the form of ordinary building blocks of calculations.

In Mathematica 10, machine learning is one of the key areas in which this happens.. All kinds of powerful fundamental algorithms are built into the core of the system: logistic regression, random forests, support vector methods (SVMs), etc. As well, all kinds of data preprocessing procedures and their evaluation. But for the user, all this is represented by two highly automated functions: Classify and Predict . Now with these features, bringing machine learning to any field is easy. In Mathematica 10 there is a huge range of new possibilities in the field of algorithmic graph theory , image processing , control theory , and in many other areas



. Sometimes it doesn’t seem surprising to anyone that at least you can have such and such a function, even though it’s actually more pleasant to have it as perfect as in Mathematica 10. However, in other cases, at first it seems impossible that the function might work.

The tasks are different. Maybe the problem is unsolvable in general or theoretically difficult to solve. Or is it badly conditioned. Or there are too many options. Or it requires too much data. It is noteworthy that usually, when using the mechanisms built into Mathematica and Wolfram Language(Wolfram language), it becomes possible to solve such problems, as well as creating functions covering a wide range of important applied problems associated with this task.

Another important task is how you can present the most diverse data in a suitable format and perform calculations on them. Its solution is the strongest side of the Wolfram Language, which is constantly being improved, and all the improvements go straight to Mathematica 10. So, for example, in Mathematica 10 there is an immediate symbolic form for the following data types: date and time , time series , geolocation , geodata , etc.



Wolfram Language has a way to symbolically represent an incredibly wide range of real-world phenomena. But what about data on these phenomena? Many of these are available in the Wolfram Knowledgebase ( Wolfram Knowledge Base) in the cloud. Soon we are going to launch the Wolfram Discovery Platform , which is designed for large-scale access to data from the cloud. And since this is not the usual way to use Mathematica (basic versions of Mathematica 10 are designed only for small amounts of requested data from the cloud), to expand the capabilities you will need to use the "currency" - Wolfram Cloud Credits .

However, in Mathematica10 there are many exciting new things that can be done with just a small amount of data from the Wolfram Knowledgebase (Wolfram Knowledge Base).

Some time ago I found a list of what is needed for Mathematica , which I wrote back in 1991. Some items from this list have been made for several years. But most required the development of a huge stack of technologies, the construction of which took many years. At the same time, at least one point could not be implemented all these years, up to the present time.

In this list, it was simply listed as “PDEs” (Partial Differential Equations). But behind these four letters lies hundreds of years of development of mathematics and a huge number of required algorithms and technologies. Oh sureMathematica has been able to work with PDEs (partial differential equations) for the past 20 years. But in Mathematica, we always strive for the greatest possible generality and reliability of embedded algorithms, and this is precisely the biggest difficulty. In particular, we wanted the system to cope with the PDE defined on areas of arbitrary geometry. And although there are standard methods, say, the finite element method, solutions of PDEs for various regions and bodies, they nevertheless do not provide a good enough way to describe the corresponding geometry of regions and bodies in sufficient generality.

Over the years, we have put enormous effort into developing Mathematica.and what is now called the Wolfram Language. Moreover, part of this development process has led to the development of extensive computational representations of what are traditionally regarded as mathematical concepts. This is a difficult, but fascinating, intellectual work, which consists, in essence, of studying the whole “ins and outs” of mathematics in order to recognize new, often more general, computational ideas.

A few years ago we did this for probability theory and everything that is closely connected with it, say, statistical distributions and random processes . Now, in Mathematica 10, we have done this for another area: geometry .



What we actually received is a truly fundamental extension of the concept of “domain”, which can be represented in a computational form, while it becomes an important building block for many things that will appear in the future. Based on this, Mathematica 10 created new, very powerful, features, including the solution of URP and work with finite elements.

So, what's so difficult about representing geometry in computational form? The problem is not that you need to work with different cases - there are many methods for this - but to get something really general, expandable in the future, easy to apply to all kinds of frequent and special cases. We were thinking about how to do this for more than 10 years and it's amazing to finally have a solution.

It turns out that mathematics actually does a part of this work for us - since it follows from it that there are various types of geometric objects, from points to lines, surfaces and volumes, which, from the point of view of mathematics, differ only in dimension. In computer systems, however, these objects are usually represented in completely different ways. 3D-graphic systems, for example, as a rule, work with points, lines and surfaces, but at the same time, in fact, do not have the concept of volume or body. CAD systems (CAD), on the other hand, work with volumes and bodies, but usually do not work with points, lines, and surfaces. GIS systems (GIS) can work with the boundaries and internal points of regions, but only in two-dimensional space (on the plane).

So why can't we just use math? The problem is that special mathematical theories - and representations - give, again, the opportunity to work, or, at least, are suitable, only for special cases. So, for example, you can describe geometric objects in terms of equations and inequalities, in fact, using algebraic geometry in the field of real numbers - but in fact it is convenient only for simple "mathematical" areas. You can use a combinatorial topology, which is essentially based on a grid representation of areas and is really quite a general method that is very difficult to use directly, and it also works with great difficulty with unlimited areas. Or, you can use differential geometry that works well with manifolds,

What we created works, in essence, "like mathematics": it is a general symbolic representation of geometric objects, which makes it convenient to use any of these various mathematical or computational approaches. And instead of having different types of various concepts, such as, say, “a point in a polygon”, “a point in a grid”, “a point on a straight line”, etc., and the functions that work with them, everything in our system is based on one common RegionMember function . And just like that, concepts such as the area of ​​an area ( Area function ), the volume of an area ( Volume ), or the length of an arc ( ArcLength ), together with all their generalizations, are based on one RegionMeasure function .

As a result, we got a surprisingly uniform and powerful way of working with geometric objects, which easily works with school tasks on triangles , as well as with the most complex geometric objects from the field of physics and technology. What is also important - and characteristic of our approach to everything - is that all these geometric possibilities are deeply integrated with the whole system. So, for example, you can get a solution to an equation (or system) inside a certain area , find the maximum of a function in this area or, say, calculate the integral over this area , or you can, for that matter, solve a partial differential equationdefined in this area, with all the different kinds of boundary conditions that you can easily set.

The geometric language that we received is very simple and understandable. But it is based on a huge amount of algorithmic functionality, which is based on a large number of areas that we have developed over the past quarter century. For the average user, there are several indicators of the complexity of the device of this language, although, perhaps, the treatise, which occupies several hundred pages , devoted to all kinds of details of manually setting methods for working with finite elements in Mathematica 10 will show this more clearly.

Geometry is just one of the new areas. We strive for commonality in other areas too. So let's say in the areaimage processing , in which our system now supports the operation of most image processing operations, not only in 2D (for ordinary flat images), but also for 3D images. Or, in the field of all kinds of computations on graphs , where everything now works in a single way for both directed graphs and undirected graphs, mixed graphs, multigraphs and weighted graphs. As usual, it took the development of all kinds of new types of algorithms and methods to work with these tasks, which are actually interdisciplinary, which means they have not been studied before, although it is obvious that they can be encountered in practice.

As I said, in Mathematica10 there are things that we were able to implement because our technology stack has already reached the point where the solution to these problems becomes possible. There are others who have solved problems, including those that we have pondered over the past ten or twenty years. An example is the system of working with mathematical operations and operators in an analytical form in Mathematica 10.

In a sense, what we are doing is translating the idea of ​​symbolic representation of objects to a new level. In mathematics, we always have the opportunity to consider a variable, such as, say, x in symbolic form, so that it can correspond to any possible value. We also have functions like fwhich can also be symbolic. But what about mathematical operators, such as, for example, a derivative? It was always clear earlier that if a function is given by a certain formula, then the system will take a derivative from it. But now we have a new concept of “inert” functions and operators , which gives us a general way of working with mathematical operators in a purely symbolic form, so that now we can transform and manipulate expressions formally (identically), while preserving the meaning of these operators. This makes it possible to do many new actions - from the convenient presentation of complex expressions from vector analysis to the implementation of symbolic transformations



not only on mathematical objects, but also on programs, giving you the opportunity, say, to formally work with objects such as integrals , with all possible built-in implementations of various generalizations of things, such as, say, the Leibniz rule.

In building Mathematica 10, we continued to move forward into uncharted computational and mathematical fields. But we also worked to make Mathematica even more convenient for areas such as, for example, elementary mathematics. Sometimes the construction of concepts from elementary mathematics is a challenge, as this requires the whole community that we strive to preserve. Sometimes a very sophisticated solution is required to achieve this. But as a result, we got a wonderful and smooth transition from simple to complex. And in Mathematica 10, we again achieved this for objects such as, for example, all kinds of calculations regarding curves and areas of definition and function values .

The development of the Wolfram Language has many implications for Mathematica , which can now be seen for the first time in Mathematica10. In addition to all sorts of new options for interacting with data about the real world and objects in it, external systems, there are also some new fundamental constructions in the system itself. An example is the built-in key-value system , which introduces the “named parts” of objects throughout the system, being, in fact, the built-in database for the Wolfram Language (Wolfram Language). Another example is the general template management system , which is important for programmatically working with strings, files, or web pages.



Wolfram Language opens up huge new areas of functionality: support for new programming paradigms, new structures and new data types, new forms of deployment and new ways to integrate with other systems. With all these developments and all new products , one can begin to worry that the traditional fundamental principles on which the Mathematica system is based may become obsolete and change. But in all this there is not a drop of truth. In fact, the recent development of the Wolfram Language has further strengthened and expanded the capabilities of the traditional Mathematica paradigm .

This is partly due to new software features. Partly - the result of the realization that we have developed ways to promote a system based on a very large body of knowledge. And in part - the result of continuous strengthening and optimization of our internal R&D (R&D) process.

We are still a rather small company (about 700 people), but the results of our activities are steadily increasing. It's amazing to see what we were able to achieve in Mathematica 10. Over the 19 months ( 588 days ) since the release of Mathematica 9, we have developed more than 700 new functions and all of them are available in Mathematica 10. Existing functions are also constantly improving .

It seems to me that the fact that all this has become possible is the best tribute to the tools, team and organization that we have created, and the strength of those principles that have guided us all these years.

For most people in the software development business, the amount of R&D that was done during the development of Mathematica 10 would have seemed insane . Many would have thought that a product that was already 26 years old would simply be maintained in working condition, while it would only receive minor updates and improvements every few years. But this does not apply to Mathematica at all . Instead, 26 years after the release of its first version, it continues to grow all the time with acceleration. Soon, more new things will appear in it.

But today I am extremely pleased to announce that the fruit of the “crazy” amount of all kinds of R&D developments is already available to you: Mathematica 10 .