The fastest floating point numbers in the wild west
In the process of implementing one "counting" there was a problem with increased accuracy of calculations. The computational algorithm worked quickly on standard floating-point numbers, but when libraries for precise calculations were connected, everything began to slow down wildly. In this article, algorithms for expanding floating-point numbers using a multi-component approach will be considered, thanks to which acceleration has been achieved, since float arithmetic is implemented on a cp crystal. This approach will be useful for more accurate calculation of the numerical derivative, matrix inversion, polygon trimming, or other geometric problems. So it is possible to emulate 64bit float on video cards that do not support them.
As Nikluas Wirth has already bequeathed to us to keep the numbers at 0 and 1, so we keep them in them. And nothing, that people live in the decimal system of calculation, and the usual seemingly numbers 0.1 and 0.3 are not representable in the binary system as a finite fraction? We experience cultural shock when we make calculations on them. Of course, attempts are being made to create libraries for processors based on the decimal system and IEEE even standardized formats.
But for now, we always take into account the storage binariness and perform all the monetary calculations with libraries for accurate calculations, such as bignumber, which leads to a loss of performance. Asiki consider crypt, and in processors there is so little space for this decimal arithmetic of yours, marketers say. Therefore, a multi-component approach, when a number is stored in the form of an unreformed sum of numbers, is a convenient trick and an actively developing field in the field of theoretical informatics. Although Dekker learned to multiply correctly without loss of accuracy in 1971, ready-to-use libraries appeared much later (MPFR, QD) and not in all languages, apparently because not all supported IEEE standards, but strict proofs of calculation errors even later, for example in 2017 for double-word arithmetic.
What is the point? In bearded times, when there were no standards for floating numbers to avoid problems with the implementation of their rounding, Møller came up with, and Knuth later proved that there is a summation free from errors. Doing so
This algorithm assumed that if then their exact sum can be represented as the sum of two numbers
then their exact sum can be represented as the sum of two numbers  and you can store them in pairs for subsequent calculations, and the subtraction is reduced to addition with a negative number.
and you can store them in pairs for subsequent calculations, and the subtraction is reduced to addition with a negative number.
Subsequently, Dekker showed that if floating-point numbers are used that use rounding to the nearest even number (round-to-nearest ties to even, which is generally a correct procedure that does not lead to large errors in the long calculation process and the IEEE standard), then there is an error-free multiplication algorithm.
where split () is Mr. Veltkamp's algorithm for dividing the number
using a constant which is equated to slightly more than half the length of the mantissa, which does not lead to an overflow of numbers in the multiplication process and divides the mantissa into two halves. For example, if the word length is 64-bit, the length of the mantissa is 53 and then s = 27.
which is equated to slightly more than half the length of the mantissa, which does not lead to an overflow of numbers in the multiplication process and divides the mantissa into two halves. For example, if the word length is 64-bit, the length of the mantissa is 53 and then s = 27.

Thus, Dekker provided an almost complete set required for the calculation in double-word arithmetic. Since there it was also indicated how to multiply, divide and square two double-word numbers.
He had the quickTwoSum algorithm “inline” everywhere for summing up two double-words, and the check was used . On modern processors, as described in [4], it is cheaper to use additional operations with numbers than the branching algorithm. Therefore, the following algorithm is now more appropriate for adding two single-word numbers
. On modern processors, as described in [4], it is cheaper to use additional operations with numbers than the branching algorithm. Therefore, the following algorithm is now more appropriate for adding two single-word numbers
And this is how summation and multiplication of double-word numbers is performed.
Generally speaking, the most complete and accurate list of algorithms for double-word arithmetic, theoretical error boundaries and practical implementation is described in reference [3] from 2017. Therefore, if interested, I strongly recommend to go there immediately. And in general, in [6] an algorithm for quadruple-word is given, and in [5] for a multi-component extension of an arbitrary length. Only there, after each operation, the process of renormalization is used, which is not always optimal for small sizes, and the accuracy of calculations in QD is not strictly defined. In general, it is worth thinking about the limits of applicability of these approaches, of course.
It so happened that almost all libraries for accurate calculations in js are written by one person. It creates the illusion of choice, although they are almost all the same. In addition, the documentation does not explicitly state that if you do not round the numbers after each multiply / divide operation, the size of your number will double all the time, and the complexity of the algorithm can grow to light in x3500. For example, a comparison of their calculation times might look like this if you did not round the numbers.
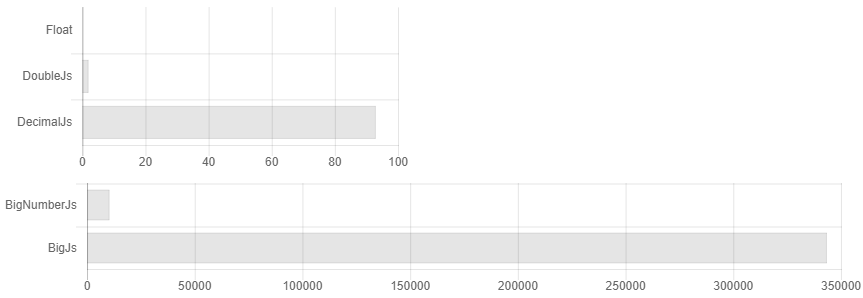
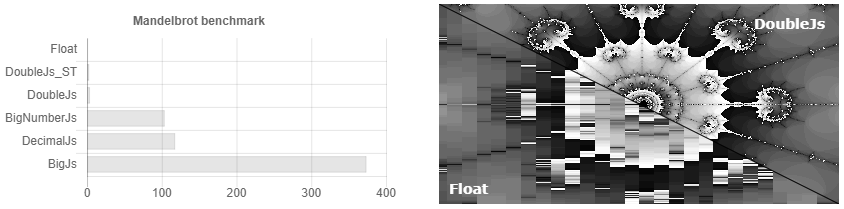
That is, you set the accuracy to 32 decimal places and ... Oops, you already have 64 characters, 128. We consider it very accurate! 256, 512 ... But I exhibited 32! .. 1024, 2048 ... Something like this appears overhead 3500 times. The documentation states that if you have scientific calculations, then decimal.js will probably be better for you. Although in fact, if you just periodically round it off, for scientific computing, Bignumber.js works a bit faster (see Fig. 1). Who then needs to count hundredths of kopecks if they cannot be given out as change? Is there any case when you need to store more than the specified numbers and do not get out a few more additional signs? How it takes the sine of such a monster number when nobody knows the exact accuracy of convergence of a taylor series for arbitrary numbers. In general, there is no groundless suspicion that there can be increased calculation speed,
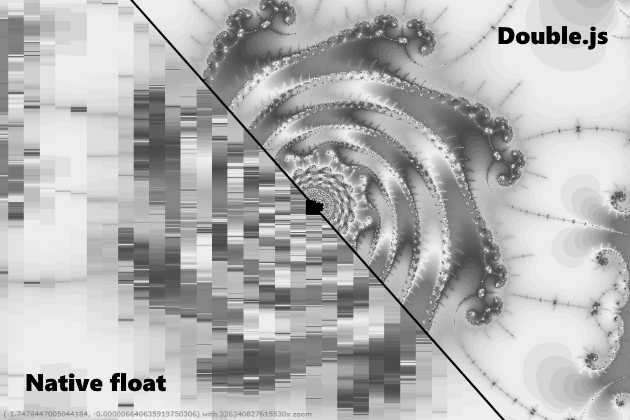
I would like to say, of course, what Double.js considers quickly and accurately. But this is not entirely true, that is, it is 10 times faster then it counts, but that's not always accurate. For example, 0.3-0.1 it can handle, moving to double storage and back. But here the number Pi is parsed with double precision of almost 32 characters and does not come back from it. An error occurs on the 16th, as if there is an overflow. In general, I urge the js community to work together to solve the problem of parsing, since I’m stuck. I tried to parse parsifrenno and divide in double precision, as in QD, divide in packs of 16 digits and divide in double precision, split the mantissa using Big.js as in one of Julia. Now I sin on a bug in .parseFloat (), since IEEE standards with rounding to the nearest integer are supported with ECMAScript 1. Although of course you can try to bind the binary buffer and watch every 0 and 1. In general, if you can solve this problem, then you can then do calculations with arbitrary precision with acceleration in x10-x20 from bignumber.js. However, the Mandelbrot set renders it qualitatively now, and you can use it for geometric problems.
Here is a link to the lib , there is an interactive benchmark and a sandbox where you can play with it.

Introduction
As Nikluas Wirth has already bequeathed to us to keep the numbers at 0 and 1, so we keep them in them. And nothing, that people live in the decimal system of calculation, and the usual seemingly numbers 0.1 and 0.3 are not representable in the binary system as a finite fraction? We experience cultural shock when we make calculations on them. Of course, attempts are being made to create libraries for processors based on the decimal system and IEEE even standardized formats.
But for now, we always take into account the storage binariness and perform all the monetary calculations with libraries for accurate calculations, such as bignumber, which leads to a loss of performance. Asiki consider crypt, and in processors there is so little space for this decimal arithmetic of yours, marketers say. Therefore, a multi-component approach, when a number is stored in the form of an unreformed sum of numbers, is a convenient trick and an actively developing field in the field of theoretical informatics. Although Dekker learned to multiply correctly without loss of accuracy in 1971, ready-to-use libraries appeared much later (MPFR, QD) and not in all languages, apparently because not all supported IEEE standards, but strict proofs of calculation errors even later, for example in 2017 for double-word arithmetic.
Double-word arithmetic
What is the point? In bearded times, when there were no standards for floating numbers to avoid problems with the implementation of their rounding, Møller came up with, and Knuth later proved that there is a summation free from errors. Doing so
functionquickTwoSum(a, b) {
let s = a + b;
let z = s - a;
let e = b - z;
return [s, e];
}
This algorithm assumed that if

Subsequently, Dekker showed that if floating-point numbers are used that use rounding to the nearest even number (round-to-nearest ties to even, which is generally a correct procedure that does not lead to large errors in the long calculation process and the IEEE standard), then there is an error-free multiplication algorithm.
functiontwoMult(a, b) {
let A = split(a);
let B = split(b);
let r1 = a * b;
let t1 = -r1 + A[0] * B[0];
let t2 = t1 + A[0] * B[1];
let t3 = t2 + A[1] * B[0];
return [r1, t3 + A[1] * B[1]];
}
where split () is Mr. Veltkamp's algorithm for dividing the number
let splitter = Math.pow(2, 27) + 1;
functionsplit(a) {
let t = splitter * a;
let d = a - t;
let xh = t + d;
let xl = a - xh;
return [xh, xl];
}
using a constant

Thus, Dekker provided an almost complete set required for the calculation in double-word arithmetic. Since there it was also indicated how to multiply, divide and square two double-word numbers.
He had the quickTwoSum algorithm “inline” everywhere for summing up two double-words, and the check was used
functiontwoSum(a, b) {
let s = a + b;
let a1 = s - b;
let b1 = s - a1;
let da = a - a1;
let db = b - b1;
return [s, da + db];
}
And this is how summation and multiplication of double-word numbers is performed.
functionadd22(X, Y) {
let S = twoSum(X[0], Y[0]);
let E = twoSum(X[1], Y[1]);
let c = S[1] + E[0];
let V = quickTwoSum(S[0], c);
let w = V[1] + E[1];
return quickTwoSum(V[0], w);
}
functionmul22(X, Y) {
let S = twoMult(X[0], Y[0]);
S[1] += X[0] * Y[1] + X[1] * Y[0];
return quickTwoSum(S[0], S[1]);
}
Generally speaking, the most complete and accurate list of algorithms for double-word arithmetic, theoretical error boundaries and practical implementation is described in reference [3] from 2017. Therefore, if interested, I strongly recommend to go there immediately. And in general, in [6] an algorithm for quadruple-word is given, and in [5] for a multi-component extension of an arbitrary length. Only there, after each operation, the process of renormalization is used, which is not always optimal for small sizes, and the accuracy of calculations in QD is not strictly defined. In general, it is worth thinking about the limits of applicability of these approaches, of course.
Horror stories javascript-a. Compare decimal.js vs bignumber.js vs big.js.
It so happened that almost all libraries for accurate calculations in js are written by one person. It creates the illusion of choice, although they are almost all the same. In addition, the documentation does not explicitly state that if you do not round the numbers after each multiply / divide operation, the size of your number will double all the time, and the complexity of the algorithm can grow to light in x3500. For example, a comparison of their calculation times might look like this if you did not round the numbers.

That is, you set the accuracy to 32 decimal places and ... Oops, you already have 64 characters, 128. We consider it very accurate! 256, 512 ... But I exhibited 32! .. 1024, 2048 ... Something like this appears overhead 3500 times. The documentation states that if you have scientific calculations, then decimal.js will probably be better for you. Although in fact, if you just periodically round it off, for scientific computing, Bignumber.js works a bit faster (see Fig. 1). Who then needs to count hundredths of kopecks if they cannot be given out as change? Is there any case when you need to store more than the specified numbers and do not get out a few more additional signs? How it takes the sine of such a monster number when nobody knows the exact accuracy of convergence of a taylor series for arbitrary numbers. In general, there is no groundless suspicion that there can be increased calculation speed,
Double.js
I would like to say, of course, what Double.js considers quickly and accurately. But this is not entirely true, that is, it is 10 times faster then it counts, but that's not always accurate. For example, 0.3-0.1 it can handle, moving to double storage and back. But here the number Pi is parsed with double precision of almost 32 characters and does not come back from it. An error occurs on the 16th, as if there is an overflow. In general, I urge the js community to work together to solve the problem of parsing, since I’m stuck. I tried to parse parsifrenno and divide in double precision, as in QD, divide in packs of 16 digits and divide in double precision, split the mantissa using Big.js as in one of Julia. Now I sin on a bug in .parseFloat (), since IEEE standards with rounding to the nearest integer are supported with ECMAScript 1. Although of course you can try to bind the binary buffer and watch every 0 and 1. In general, if you can solve this problem, then you can then do calculations with arbitrary precision with acceleration in x10-x20 from bignumber.js. However, the Mandelbrot set renders it qualitatively now, and you can use it for geometric problems.

Here is a link to the lib , there is an interactive benchmark and a sandbox where you can play with it.
Sources used
- O. Møller. Quasi double precision in floating-point arithmetic. 1965
- Theodorus Dekker. A floating-point technique for extending the available precision , 1971. [ Viewer ]
- Mioara Joldes, Jean-Michel Muller, Valentina Popescu. Tight and rigourous error arithmetic bounds for building blocks of double-word , 2017. [ PDF ]
- Muller, J.-M. Brisebarre, N. de Dinechin, etc. Handbook of Floating-Point Arithmetic, Chapter 14, 2010.
- Jonathan Shewchuk. Robust Adaptive Floating-Point Geometric Predicates , 1964. [ PDF ]
- Yozo Hida, Xiaoye Li, David Bailey. Library for Double-Double and Quad-Double Arithmetic , 2000. [ PDF ]
