BitSorting Algorithm with O (n) complexity

Background

In his free time, he decided to think about whether it would be possible to create a sizing algorithm that would have complexity O (n) would not take up a lot of additional memory and could be easily parallelized. And he achieved some result.

Imagine that we have the following set of numbers:

• 123
• 12345
• 22345
• 12345678
• 1

How will we, as humans, sort this data array? That's right, we will choose the most visually long number.
And if the length is the same, then we will compare the numbers in one category. I thought that you could just as well make the computer work.

Algorithm

So, we have at the input an array of numbers of size N:

int[] array = new int[n]

Next, we represent each element of the array in binary form and save it in a new list:

bool[][] bitMatrix = new bool[n][]; //битовая матрица нашего массива
for (int i = 0; i < array.Length; i++)
{
	BitArray bitArray = new BitArray (new int[1]{ array [i] });
	bool[] bits = new bool[bitArray.Length];
	bitArray.CopyTo (bits, 0);
	Array.Reverse (bits);
	bitMatrix [i] = bits;
}

We got the following matrix:


Then comes the most interesting part: recursive sorting.
To get started, let's look at how we would sort this bit matrix:

1. We look at the first column
2. We select all elements where the first bit is 1 in one list
3. We select all elements where the first bit is 0 in the second list
4. Repeat steps 2 and 3 for the first and second lists, but already for column number two

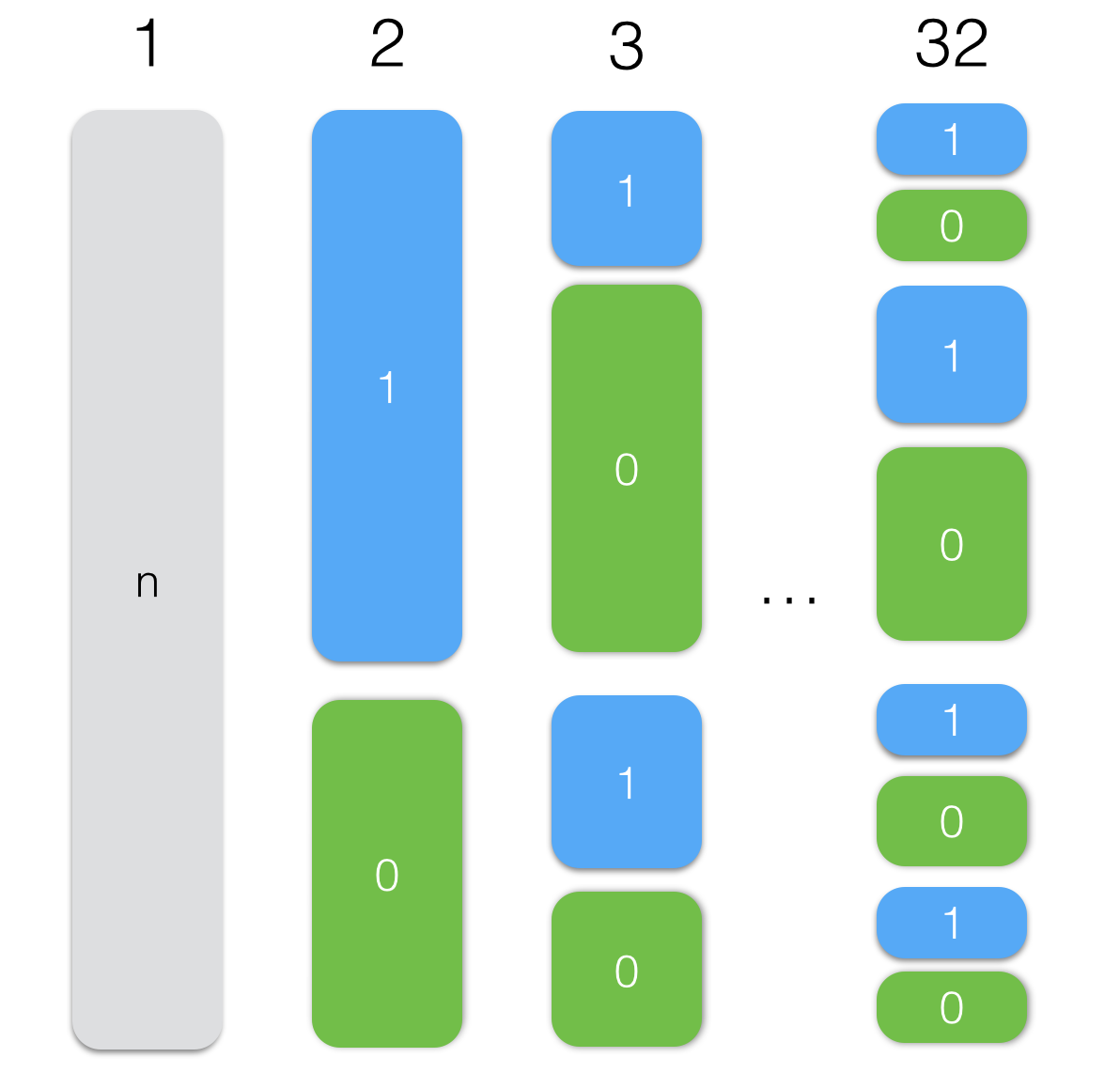
The code will look like this:

private void SortAlgorithm(bool[][] bitMatrix, int columnNumber)
{
	List ones = new List ();
	List zeros = new List ();
	for (int i = 0; i < bitMatrix.Length; i++)
	{
		if (bitMatrix[i][columnNumber])
			ones.Add(bitMatrix[i]);
		else
			zeros.Add(bitMatrix[i]);
	}
	columnNumber++;
	if (columnNumber == MAX_COLUMN_COUNT)//MAX_COLUMN_COUNT = sizeof(int)*8
	{
		sortedBitMatrix.AddRange(ones);
		sortedBitMatrix.AddRange(zeros);
		return;
	}
	if (ones.Count != 0)
		SortAlgorithm (ones.ToArray(), columnNumber);
	if (zeros.Count != 0)
		SortAlgorithm (zeros.ToArray(), columnNumber);
}

sortedBitMatrix is used to store the sorted bit matrix.
To convert the bit matrix back to an array, we use the following method:

private int[] ConvertBitMatrixToArray(List bitMatrix)
{
	int[] resultArray = new int[bitMatrix.Count];
	int count = 0;
	for (int i = 0; i < bitMatrix.Count; i++)
	{
		bool[] bits = bitMatrix [i];
		Array.Reverse(bits);
		BitArray bitArray = new BitArray(bits);
		int[] tmpArray = new int[1];
		bitArray.CopyTo(tmpArray, 0);
		resultArray [count] = tmpArray [0];
		count++;
	}
	return resultArray;
}

The result of the method will be a sorted array.

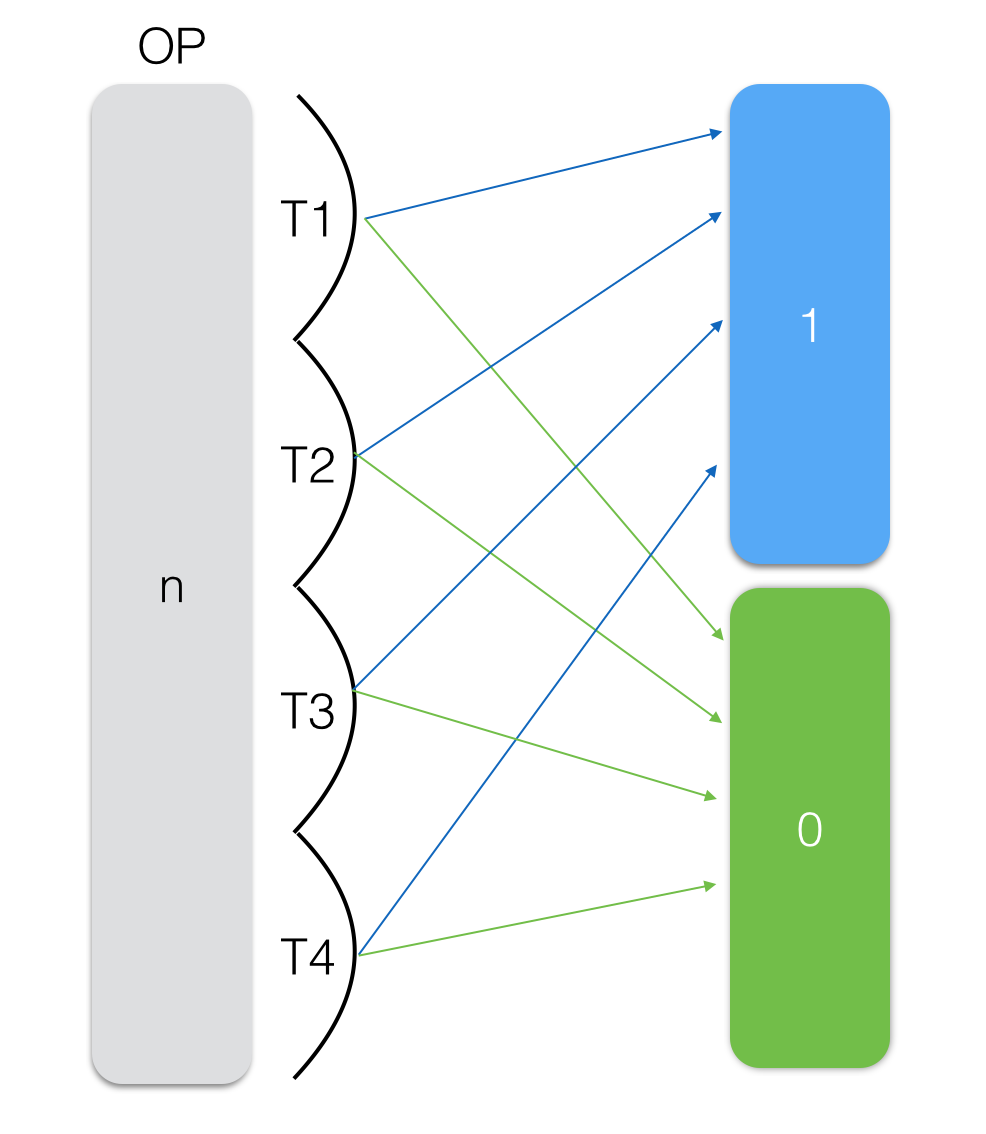
But what about parallelization?

Since most of the time is spent on passing through each column of the bit matrix in search of ones and zeros, this process can be started in several threads.
Each thread will look for ones and zeros in the matrix part:

Complexity

To sort a given array, we need the following iterations:

1. Creating a bit matrix: n
2. Search for zeros and ones: 32n
3. Convert Sorted Bit Matrix: n

Total: 34n, which is O (n)

Your opinion is interesting.
Thanks for attention.

PS github.com/koljaka/BitSorting