Experience in developing an intelligent tutorial interface
In the future, traditional teaching in the exact sciences can be supplemented not only by MOOC (Massive Open Online Courses) courses, but also by courses in “follow-up” intellectual educational programs. Such programs are able to some extent evaluate the student’s decision on completeness and correctness, as well as provide tips on the solution. The figure below shows the input interface for solving a problem in a “follow-up” training program developed by our team:

Some idea of the algorithms that underlie such programs can be found here .
In the developed program, two input interfaces for solving the problem are available: “difficult” and “easy”. Below is a more detailed description of each of them.
As a solution step, the student enters into the program formulas in LaTeX-like syntax. The syntax for entering formulas has been somewhat simplified. For example, entering matrices is as follows:
During the input of the formula, its visual representation is dynamically formed in the form of input step. After the student enters the formula, he clicks on the button “Check step”. If the step is correct, then the tested formula moves to the area with the heading "Solution". Otherwise, some elements of the step input form are colored red.
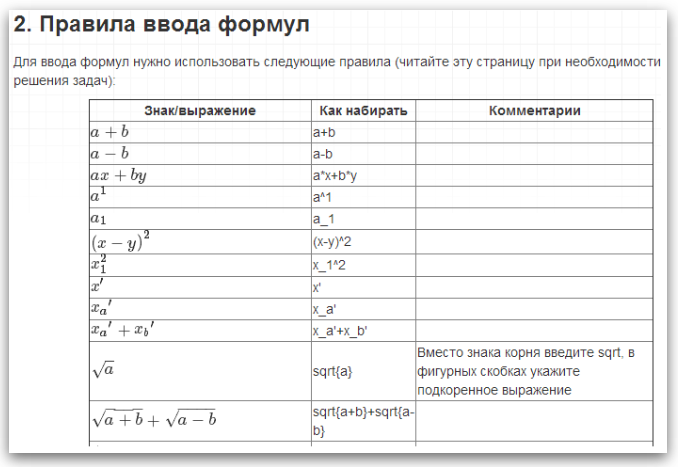
At any time, the student can look at the rules for entering formulas by clicking on the button with the corresponding name. The rules for entering formulas were written as briefly as possible, in the form of examples with explanations:
The reader may wonder why we did not build in the program a visual formula editor. The fact is that in this case, students would send too many formulas for verification, the correctness of which would be difficult to establish. Unfortunately, in order to make it possible to programmatically evaluate the course of a student’s reasoning, it is necessary to impose restrictions on the way of entering decision steps. The severity of the restrictions as the code base of the program develops can be reduced.
In the current version of the program, such restrictions apply (these are fragments from the help on the program interface):


The following figure shows that the student’s step was recognized as incorrect, due to the fact that the student used the designation not provided for in the task settings:

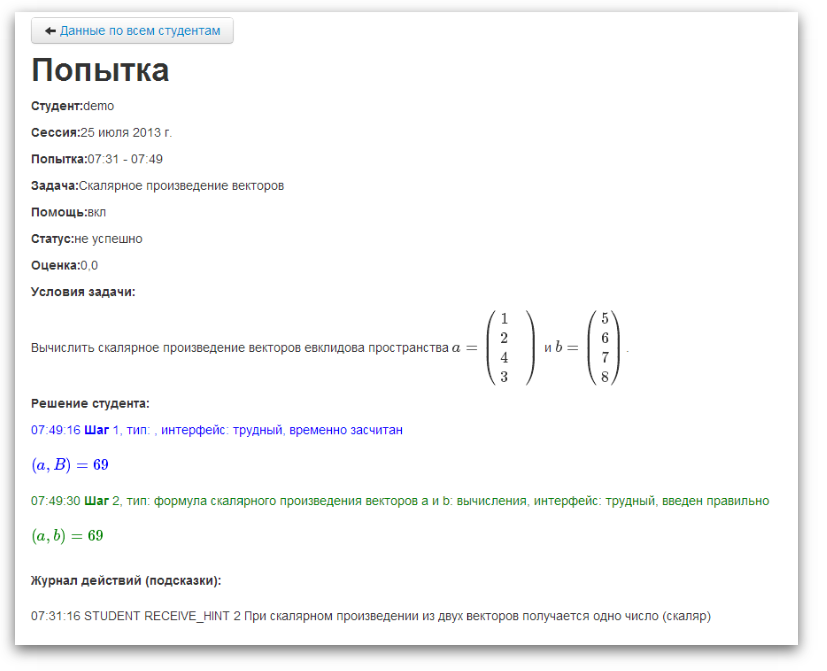
Since the student can always enter a decision step not foreseen by the course author, the complaint mechanism was implemented in the program, the essence of which is as follows. If, according to the student, the program is wrong, without counting his step as correct, then he can click on the Complain button. After that, the step will be counted as correct. Subsequently, the status of the step can be changed by the teacher. Reports on problem solving are available to the teacher in the administrative panel of the application, where such steps are highlighted and given a special status:
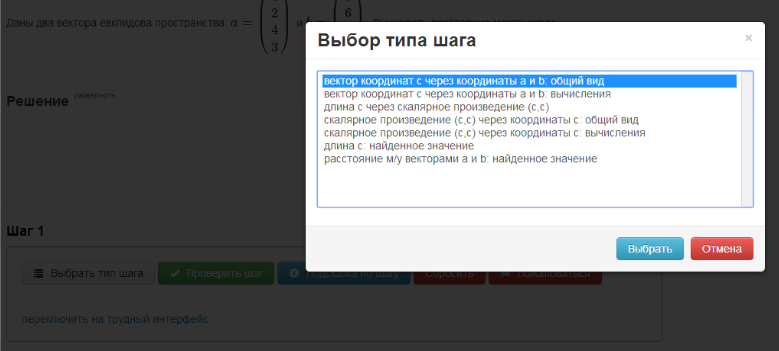
When using this interface, the student first selects the desired step type (the step types are entered into the program by the course author):
After that, the formula template is loaded into the step input form:

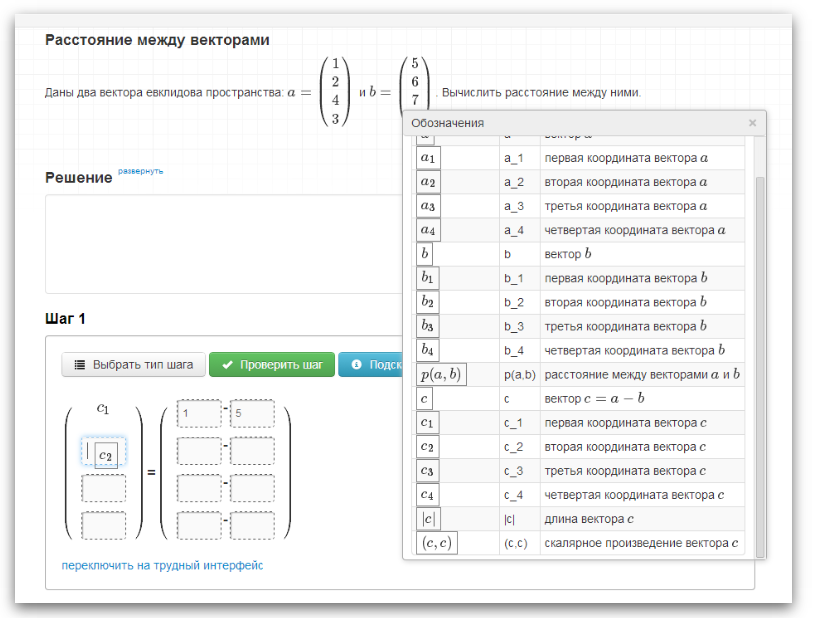
Next, the student fills in the gaps in the template by entering numbers with his hands, and drags the notation from the “Notation” window :
We can say that usability testing (or rather, its semblance, as far as the forces and timing allowed) was carried out twice. For the first time, several full-time students and evening students of the psychological faculty of one state university were caught. Students were asked to go through tutorials that help to master the program interface. Tutorials included theoretical material and two tasks. Student feedback was collected, in addition, videos of student work in the program were analyzed. The video recorded not only what was happening on the student’s screen, but also his face.
For the second time, a whole group of full-time students worked in the curriculum, who were offered the opportunity to get an automatic assessment for an exam if they successfully completed tasks in the curriculum. At this stage, video recordings of students' work, as well as their solutions, were analyzed.
10 students were interviewed. The following are the feedback received. From the reviews, we, firstly, excluded uninformative ones such as “I liked everything, no comments”, and secondly, excluded what was subsequently fixed in the program. Performance data obtained from survey participants.
1. gender: wives, academic performance: cf.
2. Gender: Wives, Achievement: High
3. gender: wives, academic performance: high
4. gender: husband, performance: cf.
5. gender: women, performance: high
6. gender: husband, performance: cf.
7. gender: women, performance: high
Note that by the time the feedback was collected, the step type selection window showed not only the types of steps from the solution recommended by the teacher, but also 2-3 randomly selected from the type database. It was assumed that in this way it would be possible to “blur” a plan for solving the problem for the student, so that he himself would think about each type of step, is it really necessary here or not. Testing has shown that having such a choice confuses even the most advanced students. Many students read the name of each type of step for a long time, trying to understand what it is, and were not completely sure of their choice. Therefore, in the next version of the program there were no “extra" types.
23 students took part in testing. Both high-performing students and students with average or low academic performance participated (performance ratings were calculated based on grades for homework). Since the data for usability testing was collected indirectly (it was not the primary goal of the students' work in the program), no conclusions can be drawn from the data collected. But on the other hand, hypotheses can be put forward :)
Students were invited to undergo training in the program interface, and then try to solve one or two problems of varying complexity. Many students, in order to get a higher grade, tried to solve all three problems. Those who could not completely solve the problem in the training program handed teachers ps papers with solutions.
The average time for learning the interface of the program took 23 minutes for students with high academic performance, and 32 minutes for students with average or low academic performance. Two students with high academic performance flipped through the help on the program interface, but did not do the exercises (one of the students subsequently did not solve any of the problems). Not all students went through tutorials on the interface the way we would like. Many students, before solving problems that help to master the interface, flipped through all the pages of the tutorials, trying to understand what awaits them next. Jumped through the pages of the tutorials now forward and backward. There were enthusiasts who solved the problem to the end and struggled to achieve a 100% score, despite the fact that on the tutorial page they were asked to enter one or two steps and proceed to the next section.
Here are the wordings of the tasks that help to master the interface:


Some students skipped training on the “easy” or “difficult” interface and passed the material only on the interface in which they were going to solve. Other students missed some particular moments and completely understood the intricacies of entering data into the program already in the process of solving problems. One student studied the syntax for entering formulas quite interestingly. This student added one or another sign to the complex formula and watched how her visual representation changed, as if debugging the input of a step.
Below are data on the results of solving problems of medium and high complexity. The value of the indicator "% wrong steps" is calculated as the ratio of the number of student decision steps that the training program marked as incorrect to the total number of student decision steps. If a student knows how to solve a problem, then the corresponding indicator value characterizes the difficulty of entering a solution for a given program interface and current restrictions on the form of the formulas introduced by him. In the tables, with the designations F, A, I, students are encoded with high, medium and low academic performance.
Table 1. Data on the solutions of the task “Distance between vectors”
Table 2. Data on the solutions of the problem “Scalar products in different bases”
The complaint mechanism was used only by students who solved the most difficult problem. 4 students complained about the program, while the complaints were not substantiated in all cases. Incorrectly perceived by the program steps were met in decisions of 8 students, there were a total of 18 such steps. An analysis of these steps showed:
Despite the presence of the “Typical Mistakes” page, students often instead of several formulas entered one formula of the form
It also turned out that the program formed lower grades for the decision than this or that student expected. The reason for this is that when making decisions in the database of the training program, it was assumed that each step of the solution corresponds to two formulas: an algebraic expression with notation and a formula with direct calculations. For instance:
Students were not instructed about the expected form of writing the solution, and therefore they often omitted formulas corresponding to algebraic expressions. Meanwhile, an algorithm for measuring progress in a solution requires, first of all, algebraic expressions: the more computationally convoluted the student’s formula is, the greater the uncertainty is how he solved the problem (roughly speaking, what can be said about the student if he simply introduces the solution a = 6?)
Quite often, students first solved the problem on paper, and then introduced its solution into the training program.
Once upon a time, not only the teachers who provided students for experiments, but also the author of this post did not believe that humanities would be able to introduce formulas in LaTeX-like syntax. We were all very surprised when this turned out to be wrong (thanks to Mikhail Filonenko for the persistent offer to try just this way of entering the solution).
There is room for improvement of the current version of the training program developed by us. In order for the training program to be able to test not 3 problems in linear algebra, but much more, it is necessary to add a lot of program code.
First, you need to expand the translation modules for formulas introduced using the “simplified” syntax
All these syntaxes are similar, but have their own nuances.
Secondly, one of the key places of such systems is the decision verification module. In this direction, an algorithm for measuring progress in the student’s decision is being developed (a description of this algorithm and its alternatives requires a separate post).

Some idea of the algorithms that underlie such programs can be found here .
In the developed program, two input interfaces for solving the problem are available: “difficult” and “easy”. Below is a more detailed description of each of them.
Difficult interface
As a solution step, the student enters into the program formulas in LaTeX-like syntax. The syntax for entering formulas has been somewhat simplified. For example, entering matrices is as follows:
[1,2;3,4;5,6]
During the input of the formula, its visual representation is dynamically formed in the form of input step. After the student enters the formula, he clicks on the button “Check step”. If the step is correct, then the tested formula moves to the area with the heading "Solution". Otherwise, some elements of the step input form are colored red.
At any time, the student can look at the rules for entering formulas by clicking on the button with the corresponding name. The rules for entering formulas were written as briefly as possible, in the form of examples with explanations:

The reader may wonder why we did not build in the program a visual formula editor. The fact is that in this case, students would send too many formulas for verification, the correctness of which would be difficult to establish. Unfortunately, in order to make it possible to programmatically evaluate the course of a student’s reasoning, it is necessary to impose restrictions on the way of entering decision steps. The severity of the restrictions as the code base of the program develops can be reduced.
In the current version of the program, such restrictions apply (these are fragments from the help on the program interface):


The following figure shows that the student’s step was recognized as incorrect, due to the fact that the student used the designation not provided for in the task settings:

Since the student can always enter a decision step not foreseen by the course author, the complaint mechanism was implemented in the program, the essence of which is as follows. If, according to the student, the program is wrong, without counting his step as correct, then he can click on the Complain button. After that, the step will be counted as correct. Subsequently, the status of the step can be changed by the teacher. Reports on problem solving are available to the teacher in the administrative panel of the application, where such steps are highlighted and given a special status:

Easy interface
When using this interface, the student first selects the desired step type (the step types are entered into the program by the course author):

After that, the formula template is loaded into the step input form:

Next, the student fills in the gaps in the template by entering numbers with his hands, and drags the notation from the “Notation” window :

Testing both interfaces
We can say that usability testing (or rather, its semblance, as far as the forces and timing allowed) was carried out twice. For the first time, several full-time students and evening students of the psychological faculty of one state university were caught. Students were asked to go through tutorials that help to master the program interface. Tutorials included theoretical material and two tasks. Student feedback was collected, in addition, videos of student work in the program were analyzed. The video recorded not only what was happening on the student’s screen, but also his face.
For the second time, a whole group of full-time students worked in the curriculum, who were offered the opportunity to get an automatic assessment for an exam if they successfully completed tasks in the curriculum. At this stage, video recordings of students' work, as well as their solutions, were analyzed.
Student feedback after the first "usability testing"
10 students were interviewed. The following are the feedback received. From the reviews, we, firstly, excluded uninformative ones such as “I liked everything, no comments”, and secondly, excluded what was subsequently fixed in the program. Performance data obtained from survey participants.
1. gender: wives, academic performance: cf.
What I liked: there is an opportunity to solve the task for a person with a lack of knowledge. Tips really help. What I didn’t like: it’s too long to decide, you have to click a lot. Manually, for example, to solve the quadratic equation can be faster than using this program.
2. Gender: Wives, Achievement: High
The program is convenient in that it has everything you need on the network. No need to install and wait. It works fast. We had to work with quadratic equations only in entering the accepted notation. Lightweight, affordable, comfortable
3. gender: wives, academic performance: high
I liked: that there are all the necessary functions, there are tips. It works without a glitch. I didn’t like it: it takes too long to enter steps.
4. gender: husband, performance: cf.
It’s very convenient that the “add a step, get a hint” menu and the hints move with the cursor on the screen so that they are always visible. The inconvenience was caused by the fact that when an error occurs, the computer highlights the entire expression in red, and not the place that it cannot read, you have to look for an error.
5. gender: women, performance: high
Conveniently, there is only the likelihood of doing unnecessary work, in the case when the coefficients = 1, and they need to be divided or multiplied. Liked: there are clues.
6. gender: husband, performance: cf.
I liked the usual input of mathematical signs and function signs. <...>
7. gender: women, performance: high
I liked that you can quickly and conveniently enter characters using the training manual. User-friendly interface, everything is clear enough. When you get used to the layout of the macbook to manipulate it turns out quickly. <...> When the answer is incorrect - there are no comments on the error - it would be more convenient if there was such a function. It’s more usual to count on a sheet, so I think if I were offered to use the program now, I would first decide on the sheet and then write the results in the windows. If the school had such a program, it might be easier to study.
Note that by the time the feedback was collected, the step type selection window showed not only the types of steps from the solution recommended by the teacher, but also 2-3 randomly selected from the type database. It was assumed that in this way it would be possible to “blur” a plan for solving the problem for the student, so that he himself would think about each type of step, is it really necessary here or not. Testing has shown that having such a choice confuses even the most advanced students. Many students read the name of each type of step for a long time, trying to understand what it is, and were not completely sure of their choice. Therefore, in the next version of the program there were no “extra" types.
The results of the second "usability testing"
23 students took part in testing. Both high-performing students and students with average or low academic performance participated (performance ratings were calculated based on grades for homework). Since the data for usability testing was collected indirectly (it was not the primary goal of the students' work in the program), no conclusions can be drawn from the data collected. But on the other hand, hypotheses can be put forward :)
Students were invited to undergo training in the program interface, and then try to solve one or two problems of varying complexity. Many students, in order to get a higher grade, tried to solve all three problems. Those who could not completely solve the problem in the training program handed teachers ps papers with solutions.
The average time for learning the interface of the program took 23 minutes for students with high academic performance, and 32 minutes for students with average or low academic performance. Two students with high academic performance flipped through the help on the program interface, but did not do the exercises (one of the students subsequently did not solve any of the problems). Not all students went through tutorials on the interface the way we would like. Many students, before solving problems that help to master the interface, flipped through all the pages of the tutorials, trying to understand what awaits them next. Jumped through the pages of the tutorials now forward and backward. There were enthusiasts who solved the problem to the end and struggled to achieve a 100% score, despite the fact that on the tutorial page they were asked to enter one or two steps and proceed to the next section.
Here are the wordings of the tasks that help to master the interface:


Some students skipped training on the “easy” or “difficult” interface and passed the material only on the interface in which they were going to solve. Other students missed some particular moments and completely understood the intricacies of entering data into the program already in the process of solving problems. One student studied the syntax for entering formulas quite interestingly. This student added one or another sign to the complex formula and watched how her visual representation changed, as if debugging the input of a step.
Below are data on the results of solving problems of medium and high complexity. The value of the indicator "% wrong steps" is calculated as the ratio of the number of student decision steps that the training program marked as incorrect to the total number of student decision steps. If a student knows how to solve a problem, then the corresponding indicator value characterizes the difficulty of entering a solution for a given program interface and current restrictions on the form of the formulas introduced by him. In the tables, with the designations F, A, I, students are encoded with high, medium and low academic performance.
Table 1. Data on the solutions of the task “Distance between vectors”
| No. | Academic performance | Solved,% | Cost t min | % wrong steps | Total steps |
| 1 | I | 1 | 29th | 0.52 | 27 |
| 2 | I | 1 | 19 | 0.44 | 16 |
| 3 | A | 1 | 12 | 0.09 | eleven |
| 4 | A | 1 | 24 | 0.76 | 29th |
| 5 | A | 1 | 29th | 0.56 | 23 |
| 6 | A | 1 | 33 | 0.42 | 12 |
| 7 | A | 1 | 21 | 0.6 | thirty |
| 8 | F | 1 | thirteen | 0.22 | 9 |
| 9 | F | 1 | 10 | 0.1 | 10 |
| 10 | F | 1 | 7 | 0 | 10 |
| eleven | F | 0 | 1 | 1 | 2 |
Table 2. Data on the solutions of the problem “Scalar products in different bases”
| No. | Academic performance | Solved,% | Cost t min | % wrong steps | Total steps |
| 1 | I | 0.9 | 33 | 0.46 | 28 |
| 2 | A | 1 | 35 | 0.62 | 29th |
| 3 | A | 0.8 | 33 | 0.12 | 17 |
| 4 | A | 0.5 | 23 | 0.45 | 22 |
| 5 | A | 0.5 | 80 | 0.41 | 54 |
| 6 | A | 0.9 | 26 | 0.17 | thirty |
| 7 | F | 0.5 | 80 | 0.76 | 49 |
| 8 | F | 0.5 | 43 | 0.73 | 25 |
| 9 | F | 0.5 | 18 | 0.25 | 16 |
| 10 | F | 0.5 | 39 | 0.2 | fifteen |
| eleven | F | 0.2 | 70 | 0.79 | 29th |
| 12 | F | 1 | 78 | 0.61 | 18 |
| thirteen | F | 0.7 | 63 | 0.8 | 25 |
| 14 | F | 1 | 32 | 0.32 | 34 |
| fifteen | F | 1 | 22 | 0.17 | 23 |
The complaint mechanism was used only by students who solved the most difficult problem. 4 students complained about the program, while the complaints were not substantiated in all cases. Incorrectly perceived by the program steps were met in decisions of 8 students, there were a total of 18 such steps. An analysis of these steps showed:
- the most common reason was unforeseen formulas (i.e. not all possible solutions to the problem were included in the program);
- A common cause of incorrect recognition by the system of entered formulas was the case when, instead of entering formulas in the easy interface with the help of dragging the notation, the student entered the characters independently from the keyboard. This can be considered a very useful remark on the intuitiveness of the easy interface. Such an input scenario should have been envisaged.
Despite the presence of the “Typical Mistakes” page, students often instead of several formulas entered one formula of the form
(c,c) = (1-3)^2 + (2-4)^2 = 8
(c,c) = (1-3)^2 + (2-4)^2, (c,c) = 8
It also turned out that the program formed lower grades for the decision than this or that student expected. The reason for this is that when making decisions in the database of the training program, it was assumed that each step of the solution corresponds to two formulas: an algebraic expression with notation and a formula with direct calculations. For instance:
(a,b) = x_a*x_b+y_a*y_b
(a,b) = 1*2+3*4
Students were not instructed about the expected form of writing the solution, and therefore they often omitted formulas corresponding to algebraic expressions. Meanwhile, an algorithm for measuring progress in a solution requires, first of all, algebraic expressions: the more computationally convoluted the student’s formula is, the greater the uncertainty is how he solved the problem (roughly speaking, what can be said about the student if he simply introduces the solution a = 6?)
Quite often, students first solved the problem on paper, and then introduced its solution into the training program.
Conclusion
Once upon a time, not only the teachers who provided students for experiments, but also the author of this post did not believe that humanities would be able to introduce formulas in LaTeX-like syntax. We were all very surprised when this turned out to be wrong (thanks to Mikhail Filonenko for the persistent offer to try just this way of entering the solution).
There is room for improvement of the current version of the training program developed by us. In order for the training program to be able to test not 3 problems in linear algebra, but much more, it is necessary to add a lot of program code.
First, you need to expand the translation modules for formulas introduced using the “simplified” syntax
- into the syntax of Mathjax (a library that helps to dynamically form a visual representation of a formula entered by a student);
- into the syntax that the SymPy symbolic computation library will understand, with the help of which student decisions are verified.
All these syntaxes are similar, but have their own nuances.
Secondly, one of the key places of such systems is the decision verification module. In this direction, an algorithm for measuring progress in the student’s decision is being developed (a description of this algorithm and its alternatives requires a separate post).
Briefly on software implementation
- Server language and framework - Python + Django,
- Formula validation logic - its heuristic algorithms + SymPy (Python),
- Client - JavaScript + jQuery + MathJax,
- Customer Clearance - Twitter Bootstrap.
Acknowledgments
- Dmitry Dushkin legato_di for his tireless advice on various technical issues and assistance in preparing this post,
- A.Yu. Schwartz and A.N. Krichevtsu for help in creating content for the training program and students provided,
- Anatoly Panin for developing the alpha version of the program.
