February 2, 2014 at 17:35Collective Mind in Number Theory
In May, an article was published on Habré that describes the work of Yitang Zhang in the field of prime number theory, which caused great resonance in the scientific community. This article gives a brief summary of the results that the scientific community has achieved nine months after the publication of this work.
Recall that one of the important, but still unproven, hypotheses in number theory is the twin prime conjecture hypothesis, which assumes that there are infinitely many pairs of primes that differ by two, for example: (3, 5); (11, 13), etc. In this case, it is assumed, of course, that there are infinitely many primes - a fact that was proved by Euclid. In a more rigorous form, this hypothesis about twin primes can be formulated as follows
where
denotes the nth prime number. The proof of the existence of this limit leads to the proof of the original hypothesis. Zhang was the first to provide evidencethat there is a finite estimate of the interval for an infinite number of pairs of primes. Using the notation above, Zhang's result can be written as follows.
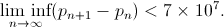
It is important to digress and say that:
1. This does not mean that all primes are spaced less than 70,000,000 apart. In fact, the greater n, the greater the average distance between two primes and the less likely it is to find a pair of primes that are a small distance from each other. See the related wikipedia article on this topic.
2. This does not mean that taking any natural number, you are guaranteed to find a prime number in the interval plus minus 70 000 000.
3. The proof is that no matter how far you go and no matter how large a natural number you take, there is always a pair of primes located further along the axis such that the interval between these primes will be less than 70,000,000.
This work caused a great resonance and encouraged many scientists to further improve this border. One of the most talented mathematicians of our time, Terence Tao, with a group of colleagues, organized a collective project polymath8a , whose goal was to reduce the proven upper bound. In just a few months, our joint efforts significantly improved the result of Zhang and proved that the
results of this work are being prepared for publication, although a draft (attention, 177 pages) can be read now.
November 19, 2013 was followed by the next breakthrough. James Maynard proved that the
ingenious Terence Tao was not at a loss and organized a new collective project, polymath8b , aimed at improving the new border. The last result says that
Thus it is known that there is an infinite number of pairs of primes, the interval between which does not exceed 270. Potentially, this boundary can be reduced to 6 if another hypothesis can be proved (in mathematics it often happens that the proof of one hypothesis follows from the proof / refutation of another - this was, for example, with Fermat's theorem).
Even in this case, however, this will not immediately lead to the ultimate goal - the proof of the twin prime hypothesis, although it will substantially bring mathematicians closer to it.
Recall that one of the important, but still unproven, hypotheses in number theory is the twin prime conjecture hypothesis, which assumes that there are infinitely many pairs of primes that differ by two, for example: (3, 5); (11, 13), etc. In this case, it is assumed, of course, that there are infinitely many primes - a fact that was proved by Euclid. In a more rigorous form, this hypothesis about twin primes can be formulated as follows
where
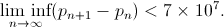
It is important to digress and say that:
1. This does not mean that all primes are spaced less than 70,000,000 apart. In fact, the greater n, the greater the average distance between two primes and the less likely it is to find a pair of primes that are a small distance from each other. See the related wikipedia article on this topic.
2. This does not mean that taking any natural number, you are guaranteed to find a prime number in the interval plus minus 70 000 000.
3. The proof is that no matter how far you go and no matter how large a natural number you take, there is always a pair of primes located further along the axis such that the interval between these primes will be less than 70,000,000.
This work caused a great resonance and encouraged many scientists to further improve this border. One of the most talented mathematicians of our time, Terence Tao, with a group of colleagues, organized a collective project polymath8a , whose goal was to reduce the proven upper bound. In just a few months, our joint efforts significantly improved the result of Zhang and proved that the
results of this work are being prepared for publication, although a draft (attention, 177 pages) can be read now.
November 19, 2013 was followed by the next breakthrough. James Maynard proved that the
ingenious Terence Tao was not at a loss and organized a new collective project, polymath8b , aimed at improving the new border. The last result says that
Thus it is known that there is an infinite number of pairs of primes, the interval between which does not exceed 270. Potentially, this boundary can be reduced to 6 if another hypothesis can be proved (in mathematics it often happens that the proof of one hypothesis follows from the proof / refutation of another - this was, for example, with Fermat's theorem).
Even in this case, however, this will not immediately lead to the ultimate goal - the proof of the twin prime hypothesis, although it will substantially bring mathematicians closer to it.