On one feature of the Kotelnikov theorem
The following task inspired me to write this article:
As is known from Kotelnikov’s theorem, in order for an analog signal to be digitized and then reconstructed, it is necessary and sufficient that the sampling frequency is greater than or equal to twice the upper frequency of the analog signal. Suppose we have a sine with a period of 1 second. Then f = 1 ∕ T = 1 hertz, sin ((2 ∗ π ∕ T) ∗ t) = sin (2 ∗ π ∗ t), a sampling frequency of 2 hertz, a sampling period of 0.5 seconds. We substitute values that are multiples of 0.5 seconds into the formula for the sine sin (2 ∗ π ∗ 0) = sin (2 ∗ π ∗ 0.5) = sin (2 ∗ π ∗ 1) = 0
Zeros are obtained everywhere. How then can this sine be restored?
An Internet search did not give an answer to this question, the maximum that could be found was various discussions on forums where rather bizarre arguments for and against were given up to links to experiments with various filters. It should be pointed out that Kotelnikov’s theorem is a mathematical theorem and should only be proved or disproved by mathematical methods. What I did. It turned out that there were a lot of proofs of this theorem in various textbooks and monographs, but I could not find where this contradiction arises for a long time, since the proofs were given without many subtleties and details. I will also say that the very formulation of the theorem in different sources was different. Therefore, in the first section I will give a detailed proof of this theorem, following the original work of the academician himself (V.A. Kotelnikov ' On the bandwidth of "ether" and wire in telecommunications. ' Materials for the I All-Union Congress on the technical reconstruction of communications and the development of low-current industry. 1933)
We formulate the theorem as given in the original source:
Any function F (t) consisting of frequencies from 0 to f1 periods per second can be represented next to
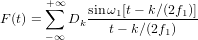
where k is an integer; ω = 2πf1; Dk are constants depending on F (t).
Proof: Any function F (t) satisfying the Dirichlet conditions (a finite number of maxima, minima, and discontinuity points on any finite interval) and integrable in the range from −∞ to + ∞, which is always the case in electrical engineering, can be represented by the Fourier integral:

those. as the sum of an infinite number of sinusoidal oscillations with frequencies from 0 to + ∞ and amplitudes C (ω) dω and S (ω) dω, depending on the frequency. Moreover,
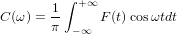
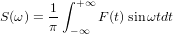
in our case, when F (t) consists only of frequencies from 0 to f1, it is obvious
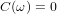
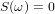
for

and therefore F (t) can be represented as follows:
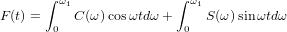
the functions C (ω) and S (ω), like any other on the site,
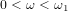
can always be represented by Fourier series, and these series can, at our request, consist of only cosines or sines, if we take the double length of the site for the period, those. 2ω1.
Author's note: an explanation is needed here. Kotelnikov takes the opportunity to supplement the functions C (ω) and S (ω) in such a way that C (ω) becomes even and S (ω) is an odd function in a double section with respect to ω1. Accordingly, in the second half of the section, the values of these functions will be C (2 ∗ ω1 −ω) and −S (2 ∗ ω1 −ω). These features are reflected on a vertical axis with the coordinate ω1, and the function S (ω) also changes sign
thus

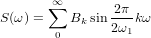
introduce the following notation
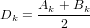
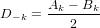
Then


Substituting obtain

transform
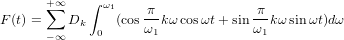
We also transform. We

integrate and replace ω1 with 2πf1:
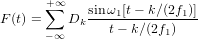 Inaccuracy in the Kotelnikov theorem. The
Inaccuracy in the Kotelnikov theorem. The
whole proof looks rigorous. What is the problem? To understand this, we turn to one not very widely known property of the inverse Fourier transform. It says that when the inverse transformation from the sum of sines and cosines to the original function, the value of this function will be equal
that is, the restored function is equal to half the value of the limits. What does this lead to? If our function is continuous, then it’s useless. But if there is a finite gap in our function, then the values of the function after the direct and inverse Fourier transforms will not coincide with the original value. Recall now the step in the proof of the theorem, where the interval is doubled. The function S (ω) is supplemented by the function −S (2 ∗ ω1 - ω). If S (ω1) (the value at the point ω1) is zero, nothing bad happens. However, if the value of S (ω1) is not equal to zero, the reconstructed function will not be equal to the original one, since at this point a discontinuity equal to 2S (ω1) occurs.
Now back to the original sine problem. As you know, the sine is an odd function, the image of which after the Fourier transform is δ (ω - Ω0) - the delta function. That is, in our case, if the sine has a frequency of ω1, we get:

Obviously, at the point ω1, two delta functions of S (ω) and −S (ω) are summed, forming zero, which we observe.
Conclusion
Kotelnikov’s theorem is certainly a great theorem. However, it must be supplemented by one more condition, namely,
in this formulation, boundary cases are excluded, in particular, the case with a sine whose frequency is equal to the boundary frequency ω1, since it is impossible to use Kotelnikov's theorem with the above condition.
As is known from Kotelnikov’s theorem, in order for an analog signal to be digitized and then reconstructed, it is necessary and sufficient that the sampling frequency is greater than or equal to twice the upper frequency of the analog signal. Suppose we have a sine with a period of 1 second. Then f = 1 ∕ T = 1 hertz, sin ((2 ∗ π ∕ T) ∗ t) = sin (2 ∗ π ∗ t), a sampling frequency of 2 hertz, a sampling period of 0.5 seconds. We substitute values that are multiples of 0.5 seconds into the formula for the sine sin (2 ∗ π ∗ 0) = sin (2 ∗ π ∗ 0.5) = sin (2 ∗ π ∗ 1) = 0
Zeros are obtained everywhere. How then can this sine be restored?
An Internet search did not give an answer to this question, the maximum that could be found was various discussions on forums where rather bizarre arguments for and against were given up to links to experiments with various filters. It should be pointed out that Kotelnikov’s theorem is a mathematical theorem and should only be proved or disproved by mathematical methods. What I did. It turned out that there were a lot of proofs of this theorem in various textbooks and monographs, but I could not find where this contradiction arises for a long time, since the proofs were given without many subtleties and details. I will also say that the very formulation of the theorem in different sources was different. Therefore, in the first section I will give a detailed proof of this theorem, following the original work of the academician himself (V.A. Kotelnikov ' On the bandwidth of "ether" and wire in telecommunications. ' Materials for the I All-Union Congress on the technical reconstruction of communications and the development of low-current industry. 1933)
We formulate the theorem as given in the original source:
Any function F (t) consisting of frequencies from 0 to f1 periods per second can be represented next to
where k is an integer; ω = 2πf1; Dk are constants depending on F (t).
Proof: Any function F (t) satisfying the Dirichlet conditions (a finite number of maxima, minima, and discontinuity points on any finite interval) and integrable in the range from −∞ to + ∞, which is always the case in electrical engineering, can be represented by the Fourier integral:

those. as the sum of an infinite number of sinusoidal oscillations with frequencies from 0 to + ∞ and amplitudes C (ω) dω and S (ω) dω, depending on the frequency. Moreover,
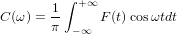
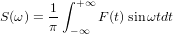
in our case, when F (t) consists only of frequencies from 0 to f1, it is obvious
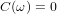
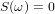
for

and therefore F (t) can be represented as follows:
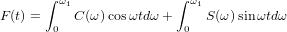
the functions C (ω) and S (ω), like any other on the site,
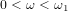
can always be represented by Fourier series, and these series can, at our request, consist of only cosines or sines, if we take the double length of the site for the period, those. 2ω1.
Author's note: an explanation is needed here. Kotelnikov takes the opportunity to supplement the functions C (ω) and S (ω) in such a way that C (ω) becomes even and S (ω) is an odd function in a double section with respect to ω1. Accordingly, in the second half of the section, the values of these functions will be C (2 ∗ ω1 −ω) and −S (2 ∗ ω1 −ω). These features are reflected on a vertical axis with the coordinate ω1, and the function S (ω) also changes sign
thus

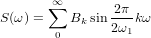
introduce the following notation
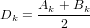
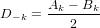
Then


Substituting obtain

transform
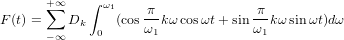
We also transform. We

integrate and replace ω1 with 2πf1:
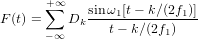 Inaccuracy in the Kotelnikov theorem. The
Inaccuracy in the Kotelnikov theorem. Thewhole proof looks rigorous. What is the problem? To understand this, we turn to one not very widely known property of the inverse Fourier transform. It says that when the inverse transformation from the sum of sines and cosines to the original function, the value of this function will be equal
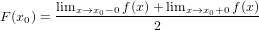
that is, the restored function is equal to half the value of the limits. What does this lead to? If our function is continuous, then it’s useless. But if there is a finite gap in our function, then the values of the function after the direct and inverse Fourier transforms will not coincide with the original value. Recall now the step in the proof of the theorem, where the interval is doubled. The function S (ω) is supplemented by the function −S (2 ∗ ω1 - ω). If S (ω1) (the value at the point ω1) is zero, nothing bad happens. However, if the value of S (ω1) is not equal to zero, the reconstructed function will not be equal to the original one, since at this point a discontinuity equal to 2S (ω1) occurs.
Now back to the original sine problem. As you know, the sine is an odd function, the image of which after the Fourier transform is δ (ω - Ω0) - the delta function. That is, in our case, if the sine has a frequency of ω1, we get:
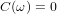

Obviously, at the point ω1, two delta functions of S (ω) and −S (ω) are summed, forming zero, which we observe.
Conclusion
Kotelnikov’s theorem is certainly a great theorem. However, it must be supplemented by one more condition, namely,
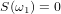
in this formulation, boundary cases are excluded, in particular, the case with a sine whose frequency is equal to the boundary frequency ω1, since it is impossible to use Kotelnikov's theorem with the above condition.
