Why is everything normal with a normal distribution?

The normal distribution (Gaussian distribution) has always played a central role in probability theory, since it arises very often as a result of the influence of many factors, the contribution of any one of which is negligible. The Central Limit Theorem (CLT) finds application in virtually all applied sciences, making the statistics apparatus universal. However, there are very frequent cases when its application is impossible, and the researchers are trying in every possible way to organize the adjustment of the results to a Gaussian. Here's an alternative approach in the case of influence on the distribution of many factors, I now will tell.
A brief history of the central heating system.Even with the living Newton, Abraham de Moirre proved a theorem on the convergence of the centered and normalized number of observations of an event in a series of independent tests to a normal distribution. Throughout the 19th and early 20th centuries, this theorem served as a scientific model for generalizations. Laplace proved the case of uniform distribution; Poisson proved the local theorem for the case with different probabilities. Poincare, Legendre and Gauss developed a rich theory of observation errors and the least squares method, based on the convergence of errors to the normal distribution. Chebyshev proved an even stronger theorem for the sum of random variables by developing the method of moments in a campaign. Lyapunov in 1900, relying on Chebyshev and Markov, proved the TSP in its current form, but only with the existence of third-order moments. And only in 1934, Feller put an end to, showing
The CLT can be formulated as follows: if random variables are independent, equally distributed and have a finite variance other than zero, then the sums (centered and normalized) of these quantities converge to the normal law. It is in this form that this theorem is taught at universities and it is so often used by observers and researchers who are not professional in mathematics. What is wrong with her? In fact, the theorem is perfectly applied in areas that Gauss, Poincaré, Chebyshev and other geniuses of the 19th century worked on, namely: the theory of observation errors, statistical physics, OLS, demographic studies, and maybe something else. But scientists who lack the originality for discoveries are engaged in generalizations and want to apply this theorem to everything, or simply drag a normal distribution over their ears, where it simply cannot exist. Want some examples
IQ coefficient. Initially, it implies that the intelligence of people is distributed normally. They conduct a test that is pre-compiled in such a way that does not take into account outstanding abilities, but takes into account individually the same shared factors: logical thinking, mental design, computational abilities, abstract thinking and something else. The ability to solve problems that are inaccessible to most, or passing a test in ultrafast time is not taken into account, and passing a test earlier increases the result (but not intelligence) in the future. And then the philistines also believe that "no one can be smarter than them two times," "let's take away and divide from the wise guys."
The second example: changes in financial indicators. The study of changes in stock prices, currency quotes, commodity options requires the use of mathematical statistics, and it is especially important here not to be mistaken with the type of distribution. A case in point: in 1997, the Nobel Prize in economics was paid for the proposal of the Black-Scholes model, based on the assumption that the distribution of growth in stock indicators (the so-called white noise) is normal. At the same time, the authors clearly stated that this model needs to be clarified, but all that most further researchers decided to do was simply add the Poisson distribution to the normal distribution. Here, obviously, there will be inaccuracies in the study of long time series, since the Poisson distribution satisfies the CLT too well, and even with 20 terms it is indistinguishable from the normal distribution. Look at the picture below (and it is from a very serious economic journal), it shows that, despite a fairly large number of observations and obvious distortions, an assumption is made that the distribution is normal.
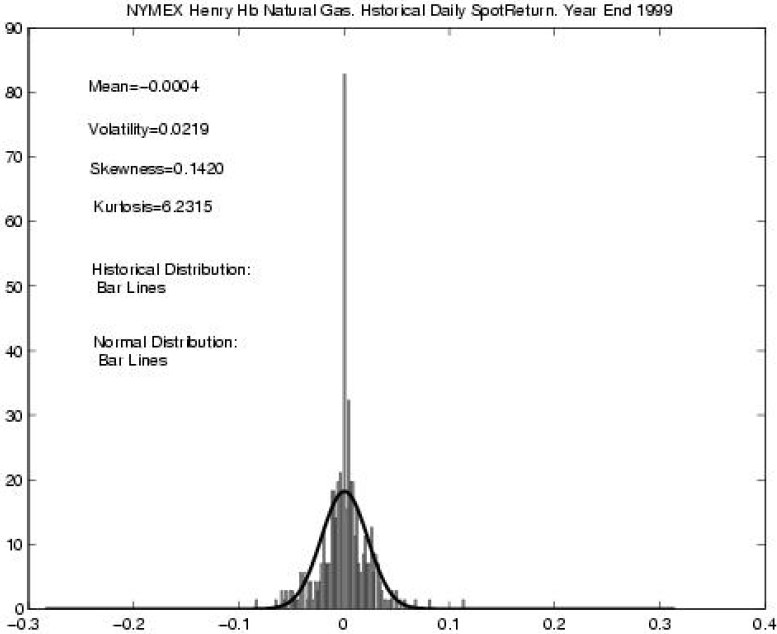
It is very obvious that the distribution of wages among the population of the city, the size of files on the disk, the population of cities and countries will not be normal.
The common feature of the distributions from these examples is the presence of the so-called “heavy tail”, that is, values far from the average, and noticeable asymmetry, usually right. Let us consider what else, apart from the normal, such distributions could be. Let's start with the previously mentioned Poisson: he has a tail, but we want the law to be repeated for a set of groups in each of which it is observed (count the size of files by enterprise, salary for several cities) or scaled (arbitrarily increase or decrease the model interval Black - Scholes), as observations show, tails and asymmetry do not disappear, but the Poisson distribution over the CLT should become normal. For the same reasons, the Erlang distribution, beta, logonormal, and all others with variance will not work. It remains only to cut off the Pareto distribution,
Distributions with the necessary properties exist and are called stable distributions. Their history is also very interesting, and the main theorem was proved a year after the work of Feller, in 1935, by the joint efforts of the French mathematician Paul Levy and the Soviet mathematician A.Ya. Khinchina. The CLT was generalized; the condition for the existence of dispersion was removed from it. Unlike normal, neither the density nor the distribution function of stable random variables is expressed (with rare exceptions, which will be discussed below), all that is known about them is the characteristic function (the inverse Fourier transform of the distribution density, but this can be understood without understanding know).
So, the theorem: if random variables are independent, equally distributed, then the sums of these quantities converge to a stable law.
Now the definition. The random variable X will be stable if and only if the logarithm of its characteristic function can be
 represented in the form:
represented in the form: 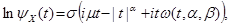
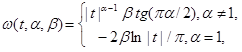
where
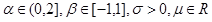 .
.In fact, there is nothing very complicated here, you just need to explain the meaning of the four parameters. The parameters sigma and mu are the usual scale and offset, as in the normal distribution, mu will be equal to the mathematical expectation, if it is, and it is when alpha is more than one. The beta parameter is asymmetry, when it is equal to zero, the distribution is symmetrical. But alpha is a characteristic parameter, it means what order the moments of the quantity exist, the closer it is to two, the more the distribution looks like normal, if two are equal, the distribution becomes normal, and only in this case it has moments of large orders, also in the case normal distribution, asymmetry degenerates. In the case when alpha is equal to one and beta is zero, the Cauchy distribution is obtained, and in the case when alpha is half,
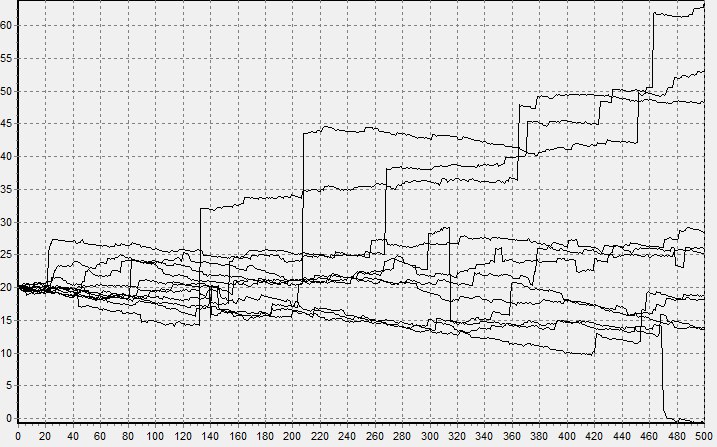
In the 20th century, a rich theory of stable quantities and processes (called Levy processes) was developed, their relationship with fractional integrals was shown, various methods of parameterization and modeling were introduced, parameters were evaluated in several ways, and the consistency and stability of estimates were shown. Look at the picture, on it is a simulated trajectory of the Levy process with a fragment enlarged by 15 times.
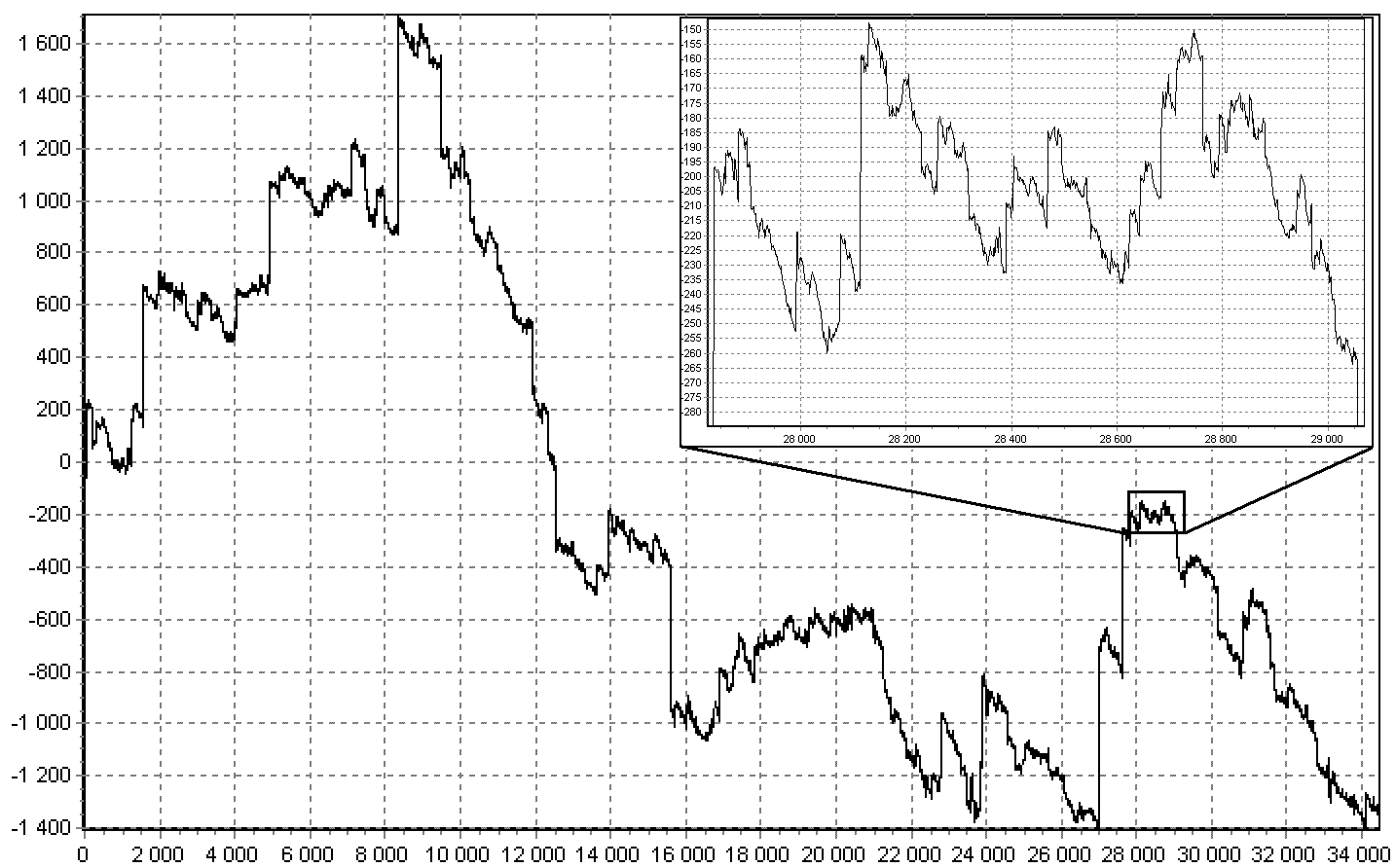
It was engaging in such processes and their application in finance that Benoit Mandelbrot invented fractals. However, not everywhere was so good. The second half of the 20th century passed under the general trend of applied and cybernetic sciences, and this meant a crisis of pure mathematics, everyone wanted to produce, but did not want to think, the humanities with their journalism occupied the mathematical sphere. Example: American Mosteller’s book “Fifty Entertaining Probabilistic Probabilistic Problems with Solutions”, Problem No. 11: The

author’s solution to this problem is simply a defeat of common sense:

The same situation is with 25 problems , where THREE contradictory answers are given.
But back to sustainable distributions. In the remainder of this article, I will try to show that there should be no additional difficulties when working with them. Namely, there are numerical and statistical methods that allow us to estimate parameters, calculate the distribution function and model them, that is, work in the same way as with any other distribution.
Modeling stable random variables. Since everything is known by comparison, I will first recall the most convenient, from the point of view of calculations, method of generating a normal quantity (Box-Muller method): if they
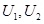 are basic random variables (uniformly distributed on [0, 1) and independent), then by the relation
are basic random variables (uniformly distributed on [0, 1) and independent), then by the relation 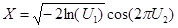
the standard normal value is obtained.
Now let us predefine alpha and beta; let Vand W , independent random variables: V is uniformly distributed on
 , W is exponentially distributed with parameter 1, we define
, W is exponentially distributed with parameter 1, we define  and
and 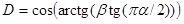 , then, by the ratio:
, then, by the ratio: 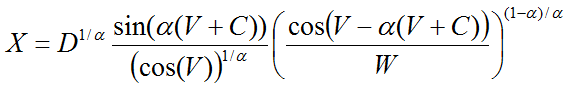
we obtain a stable random variable for which mu is zero and sigma is unity. This is the so-called standard stable value, which for the general case (with alpha not equal to unity), it is enough to multiply by the scale and add the offset. Yes, the ratio is more complicated, but it is still simple enough to use even in spreadsheets ( Link ). The figures below show the modeling trajectories of the Black - Scholes model, first for a normal and then for a stable process.

You can believe that the schedule of price changes on exchanges is more like the second.
Estimation of sustainable distribution parameters. Since it’s quite difficult to insert formulas on the Habré, I’ll just leave a link to an article where all sorts of various methods for evaluating parameters are discussed in detail, or to my articlein Russian, where only two methods are given. You can also find a wonderful book that compiles the whole theory of stable random variables and their applications (Zolotarev V., Uchaikin V. Stable Distributions and their Applications. VSP. M .: 1999.), or its purely scientific Russian version (Zolotarev V .M. Stable One-Dimensional Distributions. - M .: Nauka, Main Edition of Physics and Mathematics, 1983. - 304 p.). Methods for calculating density and distribution function are also present in these books.
As a conclusion, I can only recommend, when analyzing statistical data, when there is an asymmetry or values that are much higher than expected, ask yourself: “is the distribution law correct?” And “is everything normal with a normal distribution?”.
