Numerical methods for solving systems of nonlinear equations

Introduction

Many applied problems lead to the necessity of finding a general solution of a system of nonlinear equations. A general analytical solution of the system of nonlinear equations was not found. There are only numerical methods.

It should be noted an interesting fact that any system of equations over real numbers can be represented by one equivalent equation, if we take all the equations in the form 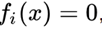, square them and add.

For the numerical solution, iterative methods of successive approximations (simple iteration) and the Newton method are used in various modifications. Iterative processes are naturally generalized to the case of a system of nonlinear equations of the form:

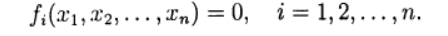(1)

Denote by the 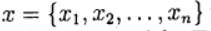vector of unknowns and define the vector function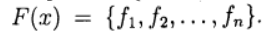Then the system (1) is written in the form of an equation:

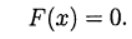(2)

Now we return to our beloved Python and note its primacy among programming languages ​​that they want to study [1].



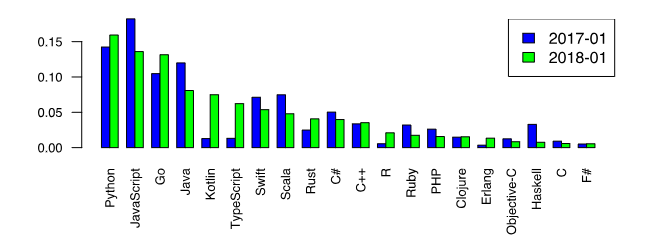
This fact is an additional incentive to consider numerical methods specifically in Python. However, among Python lovers there is an opinion that special library functions, such as scipy.optimize.root, spsolve_trianular, newton_krylov , are the best choice for solving problems by numerical methods.

It's hard not to agree with this, if only because including a variety of modules Python has risen to the top of popularity. However, there are cases when even with a superficial examination the use of direct known methods without using special functions of the SciPy library also give good results. In other words, the new is a well-forgotten old.

So, in the publication [2], on the basis of the computational experiments carried out, it was proved that the library function newton_krylov, designed to solve large systems of nonlinear equations, has two times less performance than the TSLS + WD algorithm
(two-step least squares), implemented using the NumPy library.

The purpose of this publication is to compare by the number of iterations, speed, and most importantly, by the result of solving a model problem in the form of a system of a hundred non-linear algebraic equations using the library function scipy.optimize.root and the Newton method implemented by the NumPy library.

Scipy.optimize.root solver capabilities for numerical solution of systems of algebraic nonlinear equations

The library function scipy.optimize.root is chosen as the base of comparison, because it has an extensive library of methods suitable for comparative analysis.

scipy.optimize.root ( fun, x0, args = (), method = 'hybr', jac = None, tol = None, callback = None, ptions = None )
fun - vector function to search for the root.
x0 –Initial root search conditions

method:
hybr — Powell hybrid method is used;
lm - solves systems of nonlinear equations by the least squares method.
As follows from the documentation [3] methods broyden1, broyden2, anderson, linearmixing, diagbroyden, excitingmixing, krylovNewton's exact methods. The remaining parameters are “optional” and can be found in the documentation.

Methods for solving systems of nonlinear equations

The following material can indeed be read in the literature, for example in [4], but I respect my reader and, for his convenience, I will quote the conclusion of the method, if possible in abbreviated form. Those who do not like formulas , skip this section.

In Newton's method, a new approximation for solving the system of equations (2) is determined from the solution of a system of linear equations :

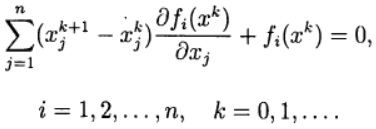(3)

We define the Jacobi matrix:

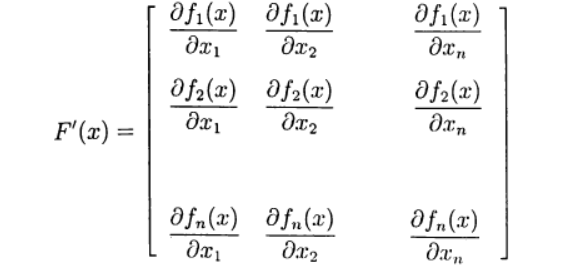(4)

We write (3) in the form:

(5)

Many one-step methods for approximate solution (2) by analogy with two-layer iterative methods for solving systems of linear algebraic equations can be written as:

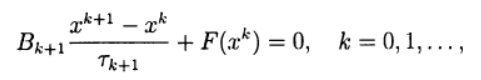(6)

where 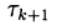are the iteration parameters, a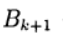- square matrix n x n, with the inverse.

When using record (6), Newton's method (5) corresponds to the choice:



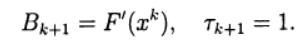
The system of linear equations (5) for finding a new approximation can be solved iteratively. In this case, we have a two-step iterative process with external and internal iterations. For example, an external iterative process can be carried out by the Newton method, and internal iterations based on the Seidel iterative method.

When solving systems of nonlinear equations, one can use direct analogs of standard iterative methods that are used to solve systems of linear equations. The non-linear Seidel method with respect to the solution (2) gives:

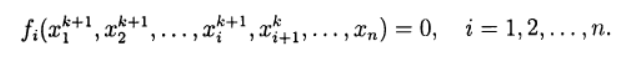(7)

In this case, each component of the new approximation from the solution of a nonlinear equation can be obtained on the basis of the simple iteration method and the Newton method in various modifications. Thus, we again arrive at a two-step iterative method, in which external iterations are carried out in accordance with the Seidel method, and internal iterations - with the Newton method.

The main computational difficulties of applying the Newton method for the approximate solution of systems of nonlinear equations are associated with the need to solve a linear system of equations with the Jacobi matrix at each iteration , and this varies from iteration to iteration. In the modified Newton method, the Jacobi matrix is ​​addressed only once:

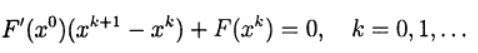(8)

Model function selection

Such a choice is not a simple task, since with an increase in the number of equations in the system in accordance with an increase in the number of variables, the result of the solution should not change, because otherwise it is impossible to track the correctness of the solution of the system of equations when comparing the two methods. I present the following solution for the model function:

n=100deff(x):
         f = zeros([n])
         for i in arange(0,n-1,1):
                  f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2
         f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3
         f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4return f

The function f creates a system of n non-linear equations, the solution of which does not depend on the number of equations and is equal to one for each of the n variables.

Program for testing on a model function with the results of solving a system of algebraic nonlinear equations using the library function optimize.root for different methods of finding the roots

from numpy import*
from scipy import optimize
import time 
ti = time.clock() 
n=100deff(x):
         f = zeros([n])
         for i in arange(0,n-1,1):
                  f[i] = (3 + 2*x[i])*x[i] - x[i-1] - 2*x[i+1] - 2
         f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3
         f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4return f
x0 =zeros([n])
sol = optimize.root(f,x0, method='krylov')
print('Solution:\n', sol.x)
print('Krylov method iteration = ',sol.nit)
print('Optimize root time', round(time.clock()-ti,3), 'seconds')

Only one of the methods described in the documentation [3] was tested according to the result of solving a model function, this is the 'krylov' method .

Solution for n = 100:

Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Krylov method iteration = 4219
Optimize root time 7.239 seconds:


Conclusion: With the increase in the number of equations, the appearance of errors in the solution is twice as noticeable. With a further increase in n, the solution becomes unacceptable, which is possible due to automatic adaptation to the step, the same reason for the sharp drop in speed. But this is just my guess.

Program for testing on a model function with the results of solving a system of algebraic nonlinear equations using a program written in Python 3, taking into account relations (1) - (8) to find the roots using the modified Newton method

Solution for n = 100:

Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Newton iteration = 13
Newton method time 0.496 seconds

Solution for n = 200:

Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1.]
Newton iteration = 14
Newton method time 1.869 seconds

To make sure that the program actually solves the system, we will rewrite the model function for avoiding the root with a value of 1 in the form:

n=10deff(x):
         f = zeros([n])
         for i in arange(0,n-1,1):
                  f[i] = (3 + 2*x[i])*x[i]*sin([i]) - x[i-1] - 2*x[i+1] - 2+e**-x[i]
         f [0] = (3 + 2*x[0] )*x[0] - 2*x[1] - 3
         f[n-1] = (3 + 2*x[n-1] )*x[n-1] - x[n-2] - 4return f

We get :
Solution:
[0.96472166 0.87777036 0.48175823 -0.26190496 -0.63693762 0.49232062
-1.31649896 0.6865098 0.89609091 0.98509235]
Newton iteration = 16
Newton method time 0.046 seconds

Output: The program also works when the model function changes.

Now let's return to the initial model function and check a wider range for n, for example, 2 and 500.
n = 2
Solution:
[1. 1.]
Newton iteration = 6
Newton method time 0.048 seconds
n = 500

Findings:

A program written in Python using the modified Newton method, when solving systems of nonlinear equations from a given model function, has a greater solution stability than when using the library function optimize.root (f, x0, method = 'krylov') for the Krylov method. Regarding the speed of the final conclusion can not be done because of the different approach to managing the step.

References:

1. Rating of programming languages ​​2018.
2. Bondar I.V., Faleichik B.V. Matrix-free iterative processes with root-mean-square error suppression for large systems of nonlinear equations.
3. scipy.optimize.root.
4. Vabishchevich P.N. Numerical methods: Computational workshop. - M .: Book House "LIBROKOM", 2010. - 320 p.