Replacing binary logic - will it increase performance?
Surely there are already a lot of posts on this topic on Habr. Nevertheless, I will try to tell my point of view on all this ...
Once I read on the Internet about the ternary number system and became interested. I was tormented by the question, but you can’t use a symmetric ternary number system (SS) at the heart of a computer, and even suddenly it will increase computer performance? It seemed to me that this was possible, and I longed to verify it.
Information: The
trinity number system is a positional number system with an integer base equal to 3. There are two versions: asymmetric and symmetric.
In an asymmetric ternary number system, the numbers {0,1,2} are more often used, and in a symmetric ternary number system the signs {-, 0, +}, {−1,0, + 1}.
For some people, this logic is difficult. They say, for example, give an example of such logic in life.
A person who thinks a little about this logic will understand that it is more vital than binary. A common example of ternary logic in life is connected with direct current: the current moves in one direction, in the other direction, it does not exist.
It turned out that the symmetric ternary number system was used a long time ago to solve the "weight problem", was used in the Setun computer , built in the 50s at Moscow State University. Since 2008, the California Polytechnic State University of San Luis Obispo has operated the TCA2 digital computer system based on the ternary number system.


What are the advantages of a ternary SS over binary? Consider these advantages:
Take the number 10 in the decimal SS and translate it into a binary SS, get 1010, translate into a ternary symmetric SS, get +0+, well, if in a ternary asymmetric SS, we get 101 From this we see that in some numbers in the ternary symmetric and asymmetric SS-ax there are fewer digits than in binary SS.
Take the number 5 in the decimal SS and translate it into a binary SS, get 101, translate into a ternary symmetric SS, then we get + -, well, if in a ternary asymmetric SS, we get 12. From this we see that in some numbers in ternary asymmetric SS has fewer digits than in binary and ternary symmetric SSs.
Trinity SS accommodates a larger range of numbers, because 3 ^ n> 2 ^ n (where n is a natural number). For example, if n = 9, then 3 ^ 9 = 19683> 2 ^ 9 = 512.
3.
Efficiency of the number system - the stock of numbers that can be written in this system using a certain number of characters. The larger the stock, the more economical the system. By the cost of the number of digits (in a three-digit decimal number 3 * 10 = 30 digits) the most economical of positional exponential asymmetric number systems. Let p denote the base of the number system, n the number of required characters. Then we get n / p digits required to record this set of characters in a given number system, and the number of numbers that can be written in this case will be equal to pn / p.
We examined ternary arithmetic, now we will touch on logic:
What are the problems of binary logic?
1. The power of a computer based on binary logic is not always enough. We give an example. One of the most sophisticated security systems is the RSA cryptosystem. Opening an RSA cipher with a key length of 1024 bits (this length is often used in information systems) will take at best fifteen years when distributed computing is performed on thousands of powerful PCs, and by then this encryption system will cease to be in demand.
Let us prove mathematically which number system will be the best for maximum power and memory capacity. To do this, consider the function f (p) = p ^ (n / p), in which p is the base of the number system, and n is the number of required characters. Then we get n / p digits required to record this set of characters in a given number system, and the number of numbers that can be written in this case will be pn / p
f (p) = p ^ (n / p)
In order to determine the maximum value of the function, we find its derivative:
ln f = ln p ^ (n / p)
ln f = n / p * ln p
... (I will not give all the mathematics here)
n * p ^ (n / p-2) it will never be 0 => (1 - ln p) = 0, ln p = 1, p = e
e = 2.71, and the nearest integer to it is three.
So, in this regard, the best system with an integer base is a ternary one.
The most delicious - consider the ternary logical operations:
1. Negation
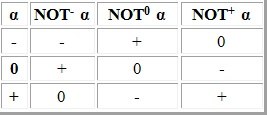
2. Conjunction - logical AND

3. Disjunction - logical OR
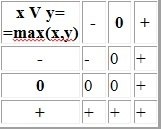
4. Operation Select . This operation exists only for ternary logic. The truth table of each of these three operations contains everywhere “-”, except for the only value that it can be selected.

5. Modification . The full name of these single-seat operations: an increase of one modulo three (INC) and a decrease of one modulo three (DEC). An increase of one modulo three is a cyclic addition of one.
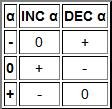
Here you can see previously familiar logical operations from binary logic, but new ones were added ...
A quantum computer is a computing device based on quantum mechanics. A quantum computer is fundamentally different from classical computers based on classical mechanics.
Due to the huge speed of decomposition into simple factors, a quantum computer will allow to decrypt messages encrypted using the popular asymmetric cryptographic RSA algorithm. Until now, this algorithm is considered relatively reliable, since an effective way of decomposing numbers into prime factors for a classical computer is currently unknown. In order, for example, to get access to a credit card, you need to decompose into two simple factors a number hundreds of digits long. Even for the fastest modern computers, this task would take hundreds of times longer than the age of the Universe. Thanks to the Shore algorithm, this task becomes quite feasible if a quantum computer is built.
The Canadian company D-Wave announced in February 2007 the creation of a sample of a quantum computer, consisting of 16 qubits. This device works on qubits - quantum analogs of bits.
But you can build computers not on bits, but on kutrits - analogues of trit in a quantum computer.
Koutrite (quantum trit) is a quantum cell that has three possible states.
The true innovation of the Lannion method is that by using quitrates instead of qubits in universal quantum gates, researchers can significantly reduce the number of gates needed.
Lannion argues that a computer that would normally use 50 traditional quantum gates can do just nine if it is based on a ternary representation.
Also, according to some studies, the use of cutrites instead of qubits will simplify the implementation of quantum algorithms and computers.
Total:
In the end, it is clear that the ternary symmetric system is better than the binary system in some respects, but does not win much. But with the advent of quantum computers, ternary computing got a new life. Universal quantum logic gates - the cornerstone of newborn quantum computing systems - require hundreds of gates to complete one useful operation. The quantum computer of the Canadian company D-Wave, announced last year, consists of only 16 quantum bits - qubits - the minimum required for the controlled NOT gate. Using cutrites in a quantum computer would have required far fewer gates to complete one operation. I think if the production and testing of such computers had begun, the results would have been better than with conventional computers, their mass production would soon have begun,
Once I read on the Internet about the ternary number system and became interested. I was tormented by the question, but you can’t use a symmetric ternary number system (SS) at the heart of a computer, and even suddenly it will increase computer performance? It seemed to me that this was possible, and I longed to verify it.
Information: The
trinity number system is a positional number system with an integer base equal to 3. There are two versions: asymmetric and symmetric.
In an asymmetric ternary number system, the numbers {0,1,2} are more often used, and in a symmetric ternary number system the signs {-, 0, +}, {−1,0, + 1}.
For some people, this logic is difficult. They say, for example, give an example of such logic in life.
A person who thinks a little about this logic will understand that it is more vital than binary. A common example of ternary logic in life is connected with direct current: the current moves in one direction, in the other direction, it does not exist.
It turned out that the symmetric ternary number system was used a long time ago to solve the "weight problem", was used in the Setun computer , built in the 50s at Moscow State University. Since 2008, the California Polytechnic State University of San Luis Obispo has operated the TCA2 digital computer system based on the ternary number system.


What are the advantages of a ternary SS over binary? Consider these advantages:
Less bits
(It is written chewed so that everyone can understand the essence of this point)Take the number 10 in the decimal SS and translate it into a binary SS, get 1010, translate into a ternary symmetric SS, get +0+, well, if in a ternary asymmetric SS, we get 101 From this we see that in some numbers in the ternary symmetric and asymmetric SS-ax there are fewer digits than in binary SS.
Take the number 5 in the decimal SS and translate it into a binary SS, get 101, translate into a ternary symmetric SS, then we get + -, well, if in a ternary asymmetric SS, we get 12. From this we see that in some numbers in ternary asymmetric SS has fewer digits than in binary and ternary symmetric SSs.
Capacity
Trinity SS accommodates a larger range of numbers, because 3 ^ n> 2 ^ n (where n is a natural number). For example, if n = 9, then 3 ^ 9 = 19683> 2 ^ 9 = 512.
3.
Cost-effective number system
Efficiency of the number system - the stock of numbers that can be written in this system using a certain number of characters. The larger the stock, the more economical the system. By the cost of the number of digits (in a three-digit decimal number 3 * 10 = 30 digits) the most economical of positional exponential asymmetric number systems. Let p denote the base of the number system, n the number of required characters. Then we get n / p digits required to record this set of characters in a given number system, and the number of numbers that can be written in this case will be equal to pn / p.
We examined ternary arithmetic, now we will touch on logic:
What are the problems of binary logic?
1. The power of a computer based on binary logic is not always enough. We give an example. One of the most sophisticated security systems is the RSA cryptosystem. Opening an RSA cipher with a key length of 1024 bits (this length is often used in information systems) will take at best fifteen years when distributed computing is performed on thousands of powerful PCs, and by then this encryption system will cease to be in demand.
Let us prove mathematically which number system will be the best for maximum power and memory capacity. To do this, consider the function f (p) = p ^ (n / p), in which p is the base of the number system, and n is the number of required characters. Then we get n / p digits required to record this set of characters in a given number system, and the number of numbers that can be written in this case will be pn / p
f (p) = p ^ (n / p)
In order to determine the maximum value of the function, we find its derivative:
ln f = ln p ^ (n / p)
ln f = n / p * ln p
... (I will not give all the mathematics here)
n * p ^ (n / p-2) it will never be 0 => (1 - ln p) = 0, ln p = 1, p = e
e = 2.71, and the nearest integer to it is three.
So, in this regard, the best system with an integer base is a ternary one.
The most delicious - consider the ternary logical operations:
1. Negation

2. Conjunction - logical AND

3. Disjunction - logical OR

4. Operation Select . This operation exists only for ternary logic. The truth table of each of these three operations contains everywhere “-”, except for the only value that it can be selected.

5. Modification . The full name of these single-seat operations: an increase of one modulo three (INC) and a decrease of one modulo three (DEC). An increase of one modulo three is a cyclic addition of one.

Here you can see previously familiar logical operations from binary logic, but new ones were added ...
Quantum computers
A quantum computer is a computing device based on quantum mechanics. A quantum computer is fundamentally different from classical computers based on classical mechanics.
Due to the huge speed of decomposition into simple factors, a quantum computer will allow to decrypt messages encrypted using the popular asymmetric cryptographic RSA algorithm. Until now, this algorithm is considered relatively reliable, since an effective way of decomposing numbers into prime factors for a classical computer is currently unknown. In order, for example, to get access to a credit card, you need to decompose into two simple factors a number hundreds of digits long. Even for the fastest modern computers, this task would take hundreds of times longer than the age of the Universe. Thanks to the Shore algorithm, this task becomes quite feasible if a quantum computer is built.
The Canadian company D-Wave announced in February 2007 the creation of a sample of a quantum computer, consisting of 16 qubits. This device works on qubits - quantum analogs of bits.
But you can build computers not on bits, but on kutrits - analogues of trit in a quantum computer.
Koutrite (quantum trit) is a quantum cell that has three possible states.
The true innovation of the Lannion method is that by using quitrates instead of qubits in universal quantum gates, researchers can significantly reduce the number of gates needed.
Lannion argues that a computer that would normally use 50 traditional quantum gates can do just nine if it is based on a ternary representation.
Also, according to some studies, the use of cutrites instead of qubits will simplify the implementation of quantum algorithms and computers.
Total:
In the end, it is clear that the ternary symmetric system is better than the binary system in some respects, but does not win much. But with the advent of quantum computers, ternary computing got a new life. Universal quantum logic gates - the cornerstone of newborn quantum computing systems - require hundreds of gates to complete one useful operation. The quantum computer of the Canadian company D-Wave, announced last year, consists of only 16 quantum bits - qubits - the minimum required for the controlled NOT gate. Using cutrites in a quantum computer would have required far fewer gates to complete one operation. I think if the production and testing of such computers had begun, the results would have been better than with conventional computers, their mass production would soon have begun,
