Compress the list of IP-addresses in the best way

Tutorial

Once I read an article on Habré about setting up BGP on a router. Instructions from there can be used to configure a home router so that traffic to specific IP addresses goes through another channel. However, there is a problem: the list of IP addresses can be very large.

In addition to networks from the list, the graph also contains the largest common subnets of neighboring networks. Read more about why this is needed.

It looked like a tree of networks from Roskomnadzor in May 2018.

At first I tried to add the entire list via / ip route add to my MikroTik hAP ac lite - the disk ran out of space on the router. Then, through BGP, I loaded all the addresses into memory - the router worked a little and hung up. It became obvious that the list should be cut.

The article mentions the network-list-parser utility from the Unsacrificed habraiser . She does what I need, but I saw her after I started reinventing my bicycle. Then I completed it out of interest, because what I got turned out to work better, albeit much slower.

So, setting the problem: you need to write a script that takes as input a list of IP addresses and networks and shortens it to the specified size. At the same time, the new list should cover all addresses from the old one, and the number of new addresses added to it should be minimal.

Let's start with the construction of the graph of all source networks (what is in the picture above). The root node is the network 0.0.0.0/0. When adding a new subnet A, we find a subnet B in the tree so that A and B are on subnet C and at the same time the size of subnet C is minimal (maximum mask). In other words, the number of common bits of subnets A and B should be maximum. We add this common subnet to the tree, and inward we transfer subnets A and B. Probably, this can be called a binary tree.

For example, to construct a tree of two subnets (192.168.0.1/32 and 192.168.33.0/24):

We get a tree:

if we add, say, a network 192.168.150.150/32, then the tree will look like this:

Orange then marked common subnet, added when building a tree. It is these common subnets that we will “collapse” to reduce the size of the list. For example, if you collapse the node 192.168.0.0/16, then we will reduce the size of the list of networks by 2 (there were 3 networks from the original list, became 1), but at the same time we will cover 65536-1-1-256 = 65278 IP addresses, which not included in our source list.

It is convenient for each node to calculate the "coefficient of benefits from collapsing", showing the number of IP addresses that will be added to each of the records removed from the list:

weight_reversed = net_extra_ip_volume / (in_list_records_count - 1)

We will use weight = 1 / weight_reversed, because it is more comfortable. It is curious that the weight can be equal to infinity, if, for example, there are two networks / 32 in the list, which together make up one large network / 31.

Thus, the greater the weight, the more profitable such a network is to collapse.

Now you can calculate the weight for all nodes in the network, sort the nodes by weight and collapse the subnets until we get the size of the list we need. However, there is a difficulty: at the moment when we collapse a network, the weights of all parent networks change.

For example, we have a tree with calculated weights:

We collapse the subnet 192.168.0.0/30: The

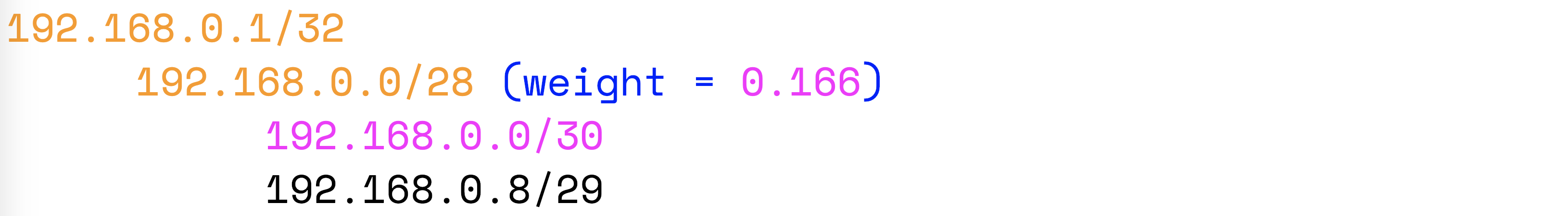
weight of the parent node has decreased. If there are nodes in the tree with a weight greater than 0.166, then the next one should collapse them already.

As a result, the list has to be compressed recursively. Algorithm like this:

We calculate the weight for all nodes.
For each node we store the maximum weight of the child node (Wmax).
It turns out that Wmax of the root node is the maximum weight of the node in the entire tree (there can be several nodes with a weight equal to Wmax).
Recursively compress all networks with a weight equal to Wmax of the root node. In this case, recalculate the weight. We return to the root node.
Wmax of the root node has decreased - we perform step 4 until we get the required size of the list of networks.

The most interesting thing is to watch the algorithm in motion. Here is an example for a list of networks: Here the subnets 192.168.0.0/24 and 192.168.150.0/24, which are identical in structure, are so clearly seen how the algorithm jumps from one branch to another during compression. Subnet 192.168.20.0/24 added in order to show that sometimes it is more profitable to compress the parent network than the child network. Note the subnet 192.168.20.0/30: after filling the tree, its weight is less than that of the parent subnet. Filling the tree: Here the black font is the real networks from the original list. Yellow - added networks. Blue is the weight of the node. Red is the current network. Pink - a collapsed network. Compression:

192.168.0.1

192.168.0.2

192.168.0.8/29

192.168.150.1

192.168.150.2

192.168.150.8/29

192.168.20.1

192.168.20.2

192.168.20.3

192.168.20.4

192.168.20.5

192.168.20.6

192.168.20.7

It was thought to speed up the algorithm of collapsing networks: to do this, it is not necessary to collapse only networks with maximum weight at each iteration. You can pre-select the value of weight, which will give us a list of the desired size. You can choose a binary search, i.e. compress with a certain weight and see what the size of the list is obtained at the output. True, for this you need two times more memory and rewrite the code - I simply did not get around.

It now remains to compare with the network-list-parser from the BGP article.

Pluses of my script:

It is more convenient to set up: just specify the required size of the list of networks, and the output will be a list of exactly that size. The network-list-parser has a lot of pens, and you need to find a combination of them.
The degree of compression is adapted to the original list. If we remove some networks from the list, we will get fewer additional addresses, if we add more. At the same time, the size of the resulting list will be constant. You can choose the maximum size that the router can handle and not worry about the list becoming too large at some point.
The resulting list contains the minimum possible number of additional networks. On the test list from GitHub, my algorithm gave 718479 additional IP addresses, and the network-list-parser gave 798761. The difference is only 10% .
How did I calculate this? We look
1. Run
```
	./network-list-parser-darwin-386-1.2.bin -src-file real_net_list_example.txt -dst-file parsed.txt -aggregation-max-fake-ips 0 -intensive-aggregation-min-prefix 31 2>&1
```
and we get a cleared list without garbage and partially reduced. I will compare the quality of compression parsed.txt. (without this step, there were problems with estimating how many fake IPs the network-list-parser adds).

2. Run
```
./network-list-parser-darwin-386-1.2.bin -src-file parsed.txt -dst-file parsed1.txt  2>&1
```
и получаем сжатый список, смотрим вывод, там есть строчка “Add 7.3% IPs coverage (798761).”

В файле parsed1.txt 16649 записей.

3. Запускаем

python3 minimize_net_list.py parsed.txt 16649.
Видим строчку ### not real ips: 718479.

I see only one drawback of the resulting script: it takes a long time and requires a lot of memory. On my MacBook list, it takes 5 seconds. On Raspberry - one and a half minutes . With RyRy3 on Mac faster, I could not deliver on Raspberry PyPy3. Network-list-parser flies both there and there.

In general, this scheme makes sense to use only perfectionists, because all the rest will spend so much computing resources for the sake of 10% of the saved networks are unlikely. Well, a little more convenient, yes.

Link to the project in GitHub

Run like this:

python3 minimize_net_list.py real_net_list_example.txt 30000 | grep -v ### > result.txt

That's all.

UPD
Pochemuk in the comments indicated an error in calculating the weight, I corrected it and now, when compressing the same list from the example with the same settings, 624925 IP addresses are added that are not included in the original list. This is already 22% better than when processing network-list-parser -th
New code in the untested branch github.com/phoenix-mstu/net_list_minimizer/tree/untested

Tags:

Compress the list of IP-addresses in the best way

Also popular now: