About two-dimensional packaging: online algorithms
 This is a continuation of the post about offline packaging algorithms.
This is a continuation of the post about offline packaging algorithms. The essence of the problem: we have a semi-infinite strip - as in tetris, only without game over, and a finite set of rectangles. The data on the rectangles comes in real time; Each new rectangle must be immediately placed and no longer moved. The goal is to minimize the overall height of the packed rectangles.
This is an online variation of the task of packing rectangles in a half-bound strip (2 Dimensional Strip Packing, 2DSP).
A little more theoretical information can be found in the previous article, but for now, without further ado, let's move on to the algorithms.
For illustration, this sequence of bricks will be used:

(Source data sponsor - random.org).
Some heuristic algorithms will be described, the general idea of which is to pre-divide the strip into regions, and place newly arriving rectangles in a particular region according to certain criteria.
Level algorithms

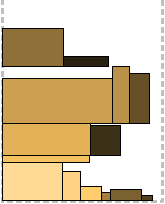

The approach of all level algorithms is that the strip is divided into levels based on the height of the rectangles available at this stage. Rectangles are placed along the base of the current level from left to right, as long as possible; a rectangle that does not fit is packed to the next level. The height of each level is determined by the highest rectangle in it. Here are three packaging options:
Next Fit Level - when the next level opens, the previous “closes” and is no longer considered;
First Fit Level - at each step of the algorithm, each level is viewed , starting from the lowest, and the rectangle is packed at the first suitable one, which has enough space;
Best Fit Level - at every step of the algorithm, all are viewedlevels, and the most suitable one is selected - the one on which after packaging there will be a minimum of space.
All three algorithms are illustrated above. At this stage, it’s easy to guess which one is where.
Algorithms NFL, FFL, BFL
Next fit level
First fit level
Best fit level
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the entire packing.
1: level = 0; h (level + 1) = 0; H = 0; i = 0
2: while there is an unpacked rectangle do
3: i ++
4: if there is sufficient space on current level then
5: pack rectangle left justified
6: if h (level + 1) <h (Li) then
7: h (level + 1) = h (Li)
8: end if
9: else [there is insufficient space on current level]
10: open a new level and pack the rectangle
11: H + = h (level + 1); level ++
12: end if
13: end while
14: print H and entire packingFirst fit level
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the entire packing.
1: level = 0; h (level + 1) = h (L1); H = h (L1); i = 1
2: while there is an unpacked rectangle do
3: i ++; level = 0
4: search for the lowest level with sufficient space
5: if such a level exists then
6: pack rectangle left justified
7: if this is the top-most level and h (level) <h (Li) then
8: h (level) = h (Li)
9: end if
10: else [there is insufficient space in all existing levels]
11: create a new level above the top-most level
12: pack rectangle left justified
13: h (level) = h (Li); H + = h (Li)
14: end if
15: end while
16: print H and entire packingBest fit level
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the entire packing.
1: level = 0; h (level + 1) = h (L1); H = h (L1); i = 0
2: while there is an unpacked rectangle do
3: i ++; level = 0
4: search for lowest level with minimum residual horizontal space
5: if such a level exists then
6: pack rectangle left justified
7: else [such a level does not exist]
8: create a new level above the top-most level
9: pack rectangle left justified
10: h (level) = h (Li); H + = h (Li)
11: end if
12: end while
13: print H and entire packingBi-Level Next Fit

Tricky modification of Next Fit Level. Two levels are created, each of which has its own strategy.
Lower level (or all odd ones): the first incoming rectangle is packed on the left edge, the rest - from right to left, while there is enough space. Then the level is closed and its height is determined by the highest rectangle in it.
Upper level (or all even ones): if there is only one rectangle on the lower level, the level is packed similarly to the lower one. If two or more, then the first rectangle is packed over the lower of the two pressed to the edges of the strip, and also pressed to the edge of the strip; all subsequent ones are packed from right to left, regardless of where the first one was packed - left or right.
It sounds confused and it is not immediately clear why such dances with a tambourine. The only thing that this algorithm obviously provides is a more even distribution of rectangles over the strip volume, without skewing to the left edge. But we will return to this strategy when we consider compression algorithms.
BiNFL Algorithm
Bi-Level Next Fit
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the entire packing.
1: level = 1; h (level) = 0; H = 0; i = 1
2: open a new bi-level
3: call 'pack on lower level'
4: print H and entire packing
Procedure 'pack on lower level'
1: the first rectangle packed is left justified
2: subsequent rectangles that fit are right justified
3: if there is insufficient space then
4: h (level) is given by the height of tallest rectangle packed
5: call 'pack on upper level'
6: end if
Procedure 'pack on the upper level'
1: if Li + 1 is the first rectangle packed then
2: left justify on top of Li
3: else
4: if Li + 2 is the first rectangle packed then
5: pack above min {h (Li); h (Li + 1)}
6: justify according to min {h (Li); h (Li + 1)}
7: else
8: if Li + j (j> 3) fits on the upper level then
9: left justify all other rectangles
10: else [rectangle does not fit]
11: H + = h (lower) + h (upper); open new bi-level
12: end if
13: end if
14: end ifShelf algorithms
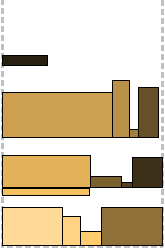

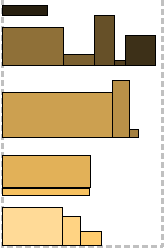
Shelf algorithms are not tied to the exact height of the rectangles and after packing the first one on the level (shelf), there is little space in case the next one is slightly higher. This “little” is regulated by the parameter r ∈ (0; 1). The height of the shelf is defined as r k , where r k + 1 <h (L i ) ≤ r k for some integer k and the height of the first packed rectangle h (L i ). Similar to tier algorithms, Next Fit, First Fit, and Best Fit shelf bypass strategies are applied. The “reserve” left on each shelf becomes profitable in the last two cases (compare FFL and FFS, BFL and BFS). In the example, p = 0.7.
NFS, FFS, BFS Algorithms
Next Fit Shelf
First fit shelf
Best fit shelf
Input: The dimensions of the rectangles {w (Li); h (Li)}
the parameter r and the strip width W.
Output: The height H and the entire packing.
1: shelf = 1; w (shelf) = 0;
h (shelf) = r ^ k for some integer k; i = 0; H = h (shelf)
2: while there is an unpacked rectangle do
3: i ++; compute k
4: if there is sufficient space and r ^ (k + 1) <h (Li) ≤ r ^ k then
5: pack rectangle to the right of the previously packed rectangle
6: else [there is insufficient space]
7: create a new shelf on top of the previous one
and pack rectangle Li on the new shelf.
8: shelf ++; H + = r ^ k
9: end if
10: end while
11: print H and entire packing.First fit shelf
Input: The dimensions of the rectangles {w (Li); h (Li)}
the parameter r and the strip width W.
Output: The height H and the entire packing.
1: shelf = 1; h (shelf) = r ^ k for some integer k;
i = 0; H = h (shelf); shelfnum = 1
2: while there is an unpacked rectangle do
3: i ++; compute k
4: search for lowest shelf of appropriate height with sufficient space
5: if such a shelf exists then
6: pack rectangle to the right of the previously packed rectangle
7: else [there is insufficient space in all shelves of
appropriate height or such a shelf does not exist]
8: create a new shelf above the top-most shelf
and pack rectangle Li on the new shelf.
9: shelf ++; H + = r ^ k; shelfnum ++
10: end if
11: end while
12: print H and entire packing.Best fit shelf
Input: The dimensions of the rectangles {w (Li); h (Li)}
the parameter r and the strip width W.
Output: The height H and the entire packing.
1: shelf = 1; h (shelf) = r ^ k for some integer k;
i = 0; H = h (shelf); shelfnum = 1
2: while there is an unpacked rectangle do
3: i ++; compute k
4: search all shelves (starting with the bottom) for one
with appropriate height and has minimum residual horizontal space.
5: if such a shelf exists then
6: pack rectangle to the right of the previously packed rectangle
7: else [there is insufficient space or
there is no shelf of appropriate height]
8: create a new shelf above the top-most shelf
and pack the rectangle Li on the new shelf.
9: shelf ++; H + = r ^ k; shelfnum ++
10: end if
11: end while
12: print H and entire packing.Harmonic shelf

Harmonic Shelf packs on one level rectangles not only with a similar height, but also with a similar width. The result will be more levels, but they will be denser filled. An additional parameter M is introduced to calculate the permissible width.
The total bandwidth, for simplicity it will take for a unit is divided into M intervals I 1 .. I M . The author claims that a reasonable value of M is in [3; 12]. The width of the intervals is calculated by the formula:
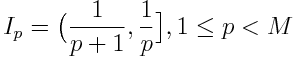 ;
; 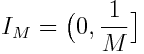
For each rectangle, p is calculated . Parameter kfor height is calculated similarly to offshore algorithms. Two conditions are checked: is there a place for the rectangle on any shelf of height r k and whether its p matches already packed there. If at least one is not fulfilled, a shelf is created for it, with blackjack and the most comfortable conditions. In the example, p = 0.7, M = 4.
HS algorithm
Harmonic shelf
Input: The dimensions of the rectangles {w (Li); h (Li)}
the parameters M, r and the strip width W.
Output: The height H and the entire packing.
1: shelf = 1; h (shelf) = r ^ k for some integer k; i = 0
2: while there is an unpacked rectangle do
3: i ++; compute k such that r ^ (k + 1) <h (Li) ≤ r ^ k
4: compute the value of p such that 1 / (p + 1) <w (Li) ≤ 1 / p
where 1 ≤ p <M
5: amongst shelves of height r ^ k find the one
with packing rectangles whose width fits in the interval Ip
6: if there is insufficient space or no rectangle of height r ^ k then
7: a new shelf of appropriate height is created above the top-most shelf
8: shelf ++
9: end if
10: if rectangle Li is the first on the shelf then
11: h (shelf) = r ^ k; H + = h (shelf)
12: end if
13: end while
14: print H and entire packingAzar y
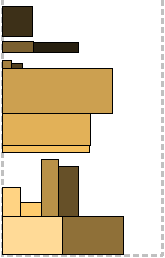
To divide into levels, a certain threshold value of 0 < Y <1/2 is introduced . The width of the rectangles is scaled in accordance with the width of the strip, which is taken as a unit. Rectangles of height 2 j -1 <h (L i ) ≤ 2 j and width 2 - x -1 <h (L i ) ≤ 2 -x are packed on one level. That is, the level is characterized by a pair ( x , j ) for some integer j and a positive integer x .
Rectangles with a width of at least Y are called bufferand each is packed on a separate level. That is, if such a rectangle is caught, an urgent need to open a new level, equal in height to it. All other (non-buffer) are packaged to the first suitable level. Suitable - in the sense of the same pair ( x , j ). If suddenly there is not enough space, a non-buffer rectangle can become the first in a new level, then the height of this level will be 2 j .
Some kind of unhealthy hierarchy, in general.
In the example, Y = 0.4.
Azar Algorithm
Azar y
Input: The dimensions of the rectangles {w (Li); h (Li)}
the parameter Y and the strip width W.
Output: The height H and the entire packing.
1: h (level) = 0; w (level) = 0; level = 0
2: while there is an unpacked rectangle do
3: if w (Li) ≥ Y then
4: level ++; w (level) = w (Li); h (level) = h (Li); H + = h (level)
5: else [w (Li) <Y]
6: compute x and j such that
2 ^ (j-1) <h (Li) ≤ 2 ^ j and 2 ^ (- x-1) <w (Li) ≤ 2 ^ (- x)
7: search for the lowest (x, j) level
8: if no (x, j) level is available or Li is blocked then
9: level ++; h (level) = 2 ^ j; H + = h (level)
10: w (level) + = w (Li)
11: else [(x, j) level is available and not blocked]
12: w (level) + = w (Li)
13: end if
14: end if
15: end while
16: print H and entire packingCompression algorithms



Compression algorithms are based on BiNFL and are essentially patches for the top-level packaging method.
The general difference is that the top level is always packed from left to right.
Compression Part Fit: For each rectangle packed to the upper level, it checks to see if there is space under it at the lower level. If you can move it to the lower level so that part of it remains on the upper level, it moves (hence Part Fit - it can partially be “pressed” to the previous level). Thus, the overall height of the second level can be reduced. He does not radically affect the packaging anymore. The first figure shows a rectangle hanging between the levels - it was shifted.
Compression Full Fit: For each rectangle packed to the upper level, it is checked whether it can completely move down to the previous level. Actually, if it can, then it is shifting. This gives us a strategic advantage: the space that was freed up in this way can be used for the next rectangle. Unfortunately, the second figure does not contain such a situation, but on it you can see two failed.
Compression Combo: Yes, this is a combination of the previous two and, accordingly, a combination of their advantages. The third figure illustrates.
Algorithms CPF, CFF, CC
Compression
Compression Part Fit
Compression Full Fit
Compression Combo
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the entire packing.
1: i = 0; H = 0
2: open new bi-level
3: packing on lower level is similar to BiNFL; H + = h (lowerlevel)
4: if there is insufficient space to pack a rectangle on the lower level then
5: call 'pack on the upper level'
6: end if
7: print H and entire packing
Procedure 'pack on the upper level'
1: while there is an unpacked rectangle do
2: if i ≥ 3 and Li is the first rectangle packed then
3: justify according to the shorter
of the left-most and right-most rectangles
4: slide rectangle downwards if there is sufficient space
and go to 12
5: else
6: if i ≥ 3 and Li is the second rectangle packed then
7: right justify and go to 12
8: else [rectangle does not fit]
9: H + = h (upperlevel); open new bi-level
10: end if
11: end if
12: end whileCompression Part Fit
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the entire packing.
1: i = 0; H = 0
2: open a new bi-level
3: packing on lower level is similar to BiNFL; H + = h (lowerlevel)
4: if there is insufficient space to pack a rectangle on the lower level then
5: call 'pack on the upper level'
6: end if
7: print H and entire packing
Procedure 'pack on the upper level'
1: while there is an unpacked rectangle do
2: if h (Li)> VerticalSpace and w (Li) ≤ HorizontalSpace then
3: shift rectangle Li downwards; go to 11
4: else
5: if h (Li) ≤ VerticalSpace and W - w (level) ≥ w (Li) then
6: left justify; go to 11
7: else [rectangle does not fit]
8: H + = h (upperlevel); open a new bi-level
9: end if
10: end if
11: end whileCompression Full Fit
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the entire packing.
1: i = 0; H = 0
2: open a new bi-level
3: packing on lower level is similar to BiNFL; H + = h (lowerlevel)
4: if there is insufficient space to pack a rectangle on the lower level then
5: call 'pack on the upper level'
6: end if
7: print H and entire packing
Procedure 'pack on the upper level'
1: while there is an unpacked rectangle do
2: if h (Li) ≤ VerticalSpace and w (Li) ≤ HorizontalSpace then
3: slide rectangle Li downwards; go to 11
4: else
5: if h (Li) ≤ VerticalSpace and W - w (level) ≥ w (Li) then
6: left justify; go to 11
7: else [rectangle does not fit]
8: H + = h (upperlevel); open new bi-level
9: end if
10: end if
11: end whileCompression Combo
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the entire packing.
1: i = 0; H = 0
2: open a new bi-level
3: packing on lower level is similar to BiNFL; H + = h (lowerlevel)
4: if there is insufficient space to pack a rectangle on the lower level then
5: call 'pack on the upper level'
6: end if
7: print H and entire packing
Procedure 'pack on the upper level'
1: while there is an unpacked rectangle do
2: if w (Li) ≤ HorizontalSpace then
3: slide rectangle Li downwards; go to 11
4: else
5: if w (Li)> HorizontalSpace and W - w (level) ≥ w (Li) then
6: left justify, go to 11
7: else [rectangle does not fit]
8: H + = h (upperlevel); open new bi-level
9: end if
10: end if
11: end whileOnline fit
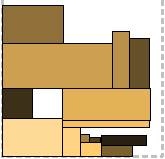
A more laborious method than the previous ones, but also more productive. Based on the Burke algorithm for an offline version of a task. I’ll probably draw some aspects.
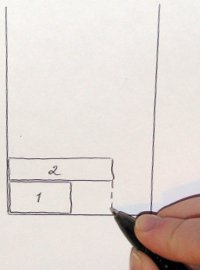

During the packaging process, Empty Areas may form, which the algorithm will try to fill in first. How they can form is seen in the photo on the left. Note that for this you need to store a certain representation of bandwidth.
After filling out of an empty area, you may get two (or it may not work out, you know).
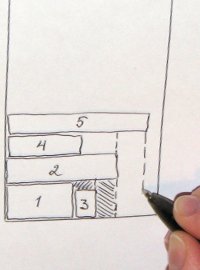
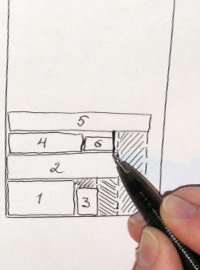 Also, several areas can be created at once with one step of the packaging - the space under the rectangle is analyzed vertically and divided by the number of "steps". In the middle photo, the splitting of an empty area into two after a rectangle is packed there again (by the way, it seems to me that in this place it would be better to split it horizontally ).
Also, several areas can be created at once with one step of the packaging - the space under the rectangle is analyzed vertically and divided by the number of "steps". In the middle photo, the splitting of an empty area into two after a rectangle is packed there again (by the way, it seems to me that in this place it would be better to split it horizontally ). In general, the farther into the forest, the more voids. At each step, the rapidly fading voids are closely examined. Here I see another optimization: you can enter a measure of the usable area and discard objectionable.
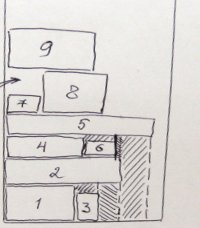 If no empty area is suitable, packaging continues with the Burke method. I remember. A height map is constructed for the strip, and the rectangle is tried on the lowest area at the moment. If it does not enter there, the low place is “filled” to the level of the nearest step, and the search is repeated. So the potential place can be pushed to the very top, and then there is another option for the formation of empty space (see right).
If no empty area is suitable, packaging continues with the Burke method. I remember. A height map is constructed for the strip, and the rectangle is tried on the lowest area at the moment. If it does not enter there, the low place is “filled” to the level of the nearest step, and the search is repeated. So the potential place can be pushed to the very top, and then there is another option for the formation of empty space (see right). The same elevation map is used at each step to identify empty areas.
In general, everything has already been said. First we try to pack in empty areas, then in the lowest place, and last but not least, from above, a degenerate case of the “lowest place”.
OF algorithm
Online fit
Input: The dimensions of the rectangles {w (Li); h (Li)} and the strip width W.
Output: The height H and the entire packing.
1: i = 0; H = 0
2: Create a linear array whose number of elements are equal to W
3: while there is an unpacked rectangle do
4: i ++
5: Search the list of empty areas for sufficient space to pack Li
6: if w (EmptyArea) ≥ w (Li) and h (EmptyArea) ≥ h (Li) then
7: pack rectangle in empty area
8: else
9: if rectangle does not fit in any of the empty areas then
10: search the linear array for available packing width
11: else [there is insufficient space in linear array]
12: pack rectangle on top left justified
from the index leading to smaller space
13: end if
14: end if
15: end while
16: H = highest entry in the linear array
17: print H and entire packingAfterword
In order to dispel the sense of aimlessness of what is happening, I will give one of the classic, but inspiring examples of the application of two-dimensional packing algorithms in a semi-limited strip. This is a task scheduler for a multiprocessor system. In modern software for clusters, more "mature" algorithms are used, but the planning task itselfcomes down to 2DSP. Under the conditions of clusters, the flow of incoming tasks is nothing more than online data for packaging: horizontal dimension - the required number of cores, vertical - the time of the task. (Everything is like at the dawn of technology: you get in line to the computer and warn in advance how much resources you need and how long your punch card will spin). The scheduler must allocate specific processors for the task and determine the start time. In its pure form, by the way, no algorithm can be used, since time is running out while the scheduler is waiting for a task or thinking about its location. Additionally, the programmer can bind the hands of various specific conditions: the priority of tasks; the ability to scale tasks at runtime; hardware delays and self-service systems, including redistribution taking into account failed resources; mapping the nature of communication within the task to the architecture of the cluster, etc.
Any algorithm is perfect in its mathematical rigor, until you begin to apply it to real life.
And finally - a comparative description of the algorithms in a pleasant, impersonal form. Here is the ratio of the optimal packing height (the sum of the areas of the rectangles divided by the width of the strip) to the obtained one.
| Nfl | Ffl | Bfl | Binfl | Nfs | Ffs | Bfs | Hs | Azar y | CPF | CFF | CC | OF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.56 | 0.63 | 0.75 | 0.56 | 0.45 | 0.57 | 0.57 | 0.37 | 0.44 | 0.60 | 0.59 | 0.63 | 0.72 |
Code (Qt):
Algorithms packager.h packager.cpp
Gui window.h window.cpp renderarea.h renderarea.cpp main.cpp
