How and why to measure FLOPS

As you know , FLOPS is a unit of measurement of computing power of computers in ( parrots ) floating-point operations, which is often used to measure who has more. It is especially important to measure FLOPS in the world of Top500 supercomputers to find out who among them is the most-most. However, the subject of measurement should have at least some practical application, otherwise what is the point of measuring and comparing it. Therefore, to clarify the capabilities of super- and just computers, there are slightly more benchmarks that are closer to real computing tasks, for example, SPEC: SPECint and SPECfp. Nevertheless, FLOPS is actively used in performance evaluations and published in reports. The Linpack test has long been used to measure it, and now they are using the open standard benchmark from LAPACK . What do these measurements give developers of high-performance and scientific applications? Is it possible to easily evaluate the performance of implementing your algorithm in FLOPSs? Will measurements and comparisons be correct? We will talk about all this below.


First, let's take a look at the terms and definitions. So, FLOPS is the number of computational operations or instructions executed on floating point operands (FP) per second. The word “computational” is used here, since the microprocessor can also execute other instructions with such operands, for example, loading from memory. Such operations do not carry a useful computational load and therefore are not taken into account.

The FLOPS value published for a particular system is a characteristic primarily of the computer itself, not the program. It can be obtained in two ways - theoretical and practical. Theoretically, we know how many microprocessors are in the system and how many executable floating-point devices are in each processor. All of them can work simultaneously and begin work on the next instruction in the pipeline every cycle. Therefore, to calculate the theoretical maximum for this system, we only need to multiply all these quantities with the processor frequency - we get the number of FP operations per second. Everything is simple, but they use such estimates, except that they are announcing in the press about future plans to build a supercomputer.

The practical measurement is to launch the Linpack benchmark. The benchmark performs the operation of multiplying the matrix by the matrix several tens of times and calculates the average value of the test execution time. Since the number of FP operations in the implementation of the algorithm is known in advance, dividing one value by another, we obtain the desired FLOPS. The Intel MKL library (Math Kernel Library) contains the LAPACK package, a package of libraries for solving linear algebra problems. The benchmark is built on the basis of this package. It is believed that its effectiveness is at the level of 90% of theoretically possible, which allows the benchmark to be considered a "reference measurement". Separately, Intel Optimized LINPACK Benchmark for Windows, Linux and MacOS can be downloaded here, or take composerxe / mkl / benchmarks in the directory if you have Intel Parallel Studio XE installed.

Obviously, developers of high-performance applications would like to evaluate the effectiveness of the implementation of their algorithms using the FLOPS metric, but already measured for their application. A comparison of the measured FLOPS with the “reference” one gives an idea of ​​how far the performance of their algorithm is from ideal and what is the theoretical potential for its improvement. To do this, you just need to know the minimum number of FP operations required to execute the algorithm, and accurately measure the execution time of the program (or part of it that performs the evaluated algorithm). Such results, along with measurements of the characteristics of the memory bus, are needed in order to understand where the implementation of the algorithm rests on the capabilities of the hardware system and what is the limiting factor: memory bandwidth, data transmission delays,



Well, now let's delve into the details in which, as you know, all evil. We have three FLOPS ratings / measurements: theoretical, benchmark and program. Consider the features of calculating FLOPS for each case.

Theoretical assessment of FLOPS for a system
To understand how the number of simultaneous operations in a processor is calculated, let's take a look at the device out-of-order block in the conveyor of an Intel Sandy Bridge processor.



Here we have 6 ports for computing devices, and, in one cycle (or processor cycle), the dispatcher can be assigned to perform up to 6 micro operations: 3 memory operations and 3 computational operations. One multiplication operation ( MUL ) and one addition ( ADD ) can be performed simultaneously , both in x87 FP units and in SSE, orAVX . Given the width of the 256 bit SIMD registers, we can get the following results:



8 MUL (32-bit) and 8 ADD (32-bit): 16 SP FLOP / cycle , i.e. 16 single precision floating point operations per cycle.
4 MUL (64-bit) and 4 ADD (64-bit): 8 DP FLOP / cycle , i.e. 8 double precision floating-point operations per cycle.

The theoretical peak FLOPS for the 1-socket Xeon E3-1275 (4 cores @ 3.574GHz) available to me is:
16 (FLOP / cycle) * 4 * 3.574 (Gcycles / sec) = 228 GFLOPS SP
8 (FLOP / cycle) * 4 * 3.574 (Gcycles / sec) = 114 GFLOPS DP

Launch of the Linpack benchmark
It starts the benchmark from the Intel MKL package on the system and we get the following results (cut for easy viewing):



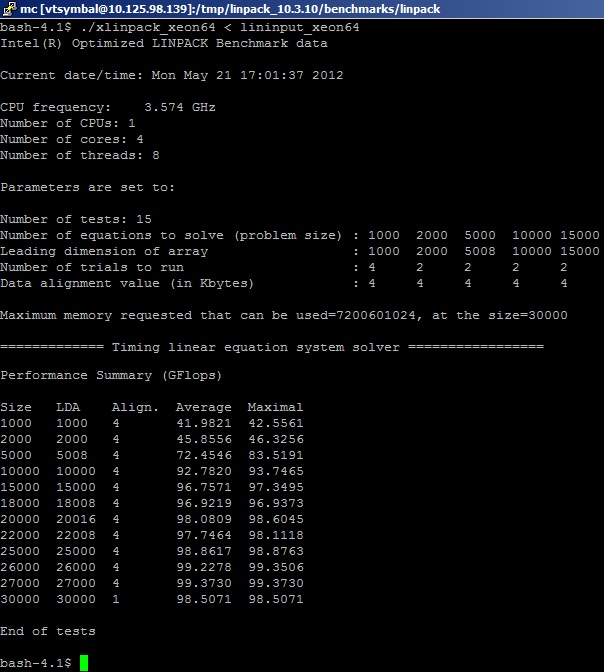
Here it is necessary to say how exactly FP operations are taken into account in the benchmark. As already mentioned, the test “knows” in advance the number of MUL and ADD operations that are necessary for matrix multiplication. In a simplified view: the system of linear equations Ax = b is solved (several thousand pieces) by multiplying dense matrixes of real numbers (real8) of size MxK, and the number of addition and multiplication operations necessary to implement the algorithm is considered (for a symmetric matrix) Nflop = 2 * (M ^ 3) + (M ^ 2). Calculations are performed for double precision numbers, as for most benchmarks. How many operations with a floating point are actually performed in the implementation of the algorithm, users do not care, although they guess that more. This is due to that matrix decomposition into blocks and transformation (factorization) are performed to achieve maximum algorithm performance on a computing platform. That is, we need to remember that in fact the value of physical FLOPS is underestimated due to the neglect of unnecessary conversion operations and auxiliary operations such as shifts.

Evaluation of the FLOPS program
To explore comparable results, we will use the do-it-yourself matrix multiplication example, that is, without the help of mathematical gurus from the MKL Performance Library development team, as our high-performance application. An example of the implementation of matrix multiplication written in C can be found in the Samples directory of the Intel VTune Amplifier XE package. We use the formula Nflop = 2 * (M ^ 3) to calculate FP operations (based on the basic matrix multiplication algorithm) and measure the time of multiplication for the case of multiply3 algorithm with the size of symmetric matrices M = 4096. In order to get efficient code, we use the optimization options –O3 (aggressive loop optimization) and –xavx(use AVX instructions) Intel C-compiler to generate vector SIMD instructions for AVX actuators. The compiler will help us find out if the matrix multiplication cycle has been vectorized. To do this, specify the –vec-report3 option . In the compilation results, we see optimizer messages: “LOOP WAS VECTORIZED” opposite the line with the body of the inner loop in the multiply.c file .



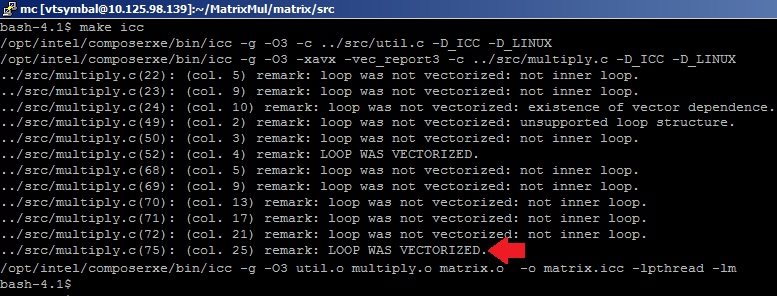
Just in case, we will check which instructions are generated by the compiler for the multiplication cycle.
$ icl –g –O3 –xavx –S
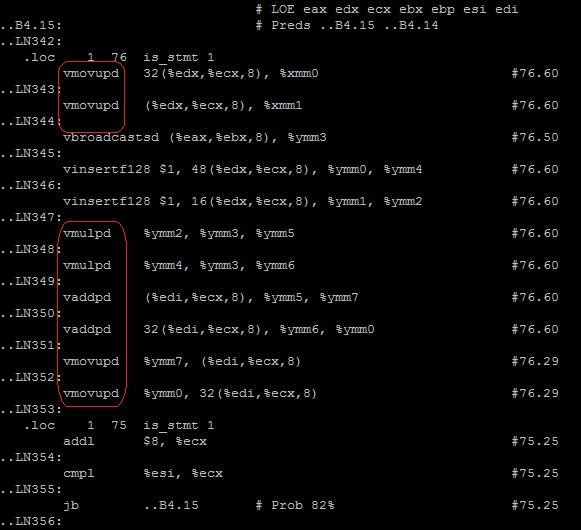
By the tag __tag_value_multiply3 we are looking for the right loop - the instructions are correct.

$ vi muliply3.s


The result of the program execution (~ 7 seconds)


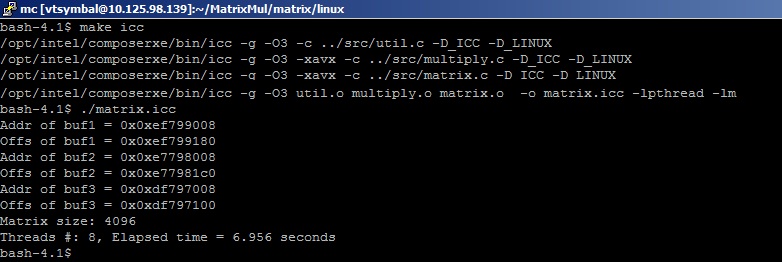
gives us the following value FLOPS = 2 * 4096 * 4096 * 4096/7 [s] =19.6 GFLOPS
The result, of course, is very far from what is obtained in Linpack, which is explained solely by the qualification gap between the author of the article and the developers of the MKL library.

Well, now the dessert! Actually, for what I started my research on this seemingly boring and long-beaten topic. A new method of measuring FLOPS.

Measuring FLOPS programs
There are problems in linear algebra, software implementation of solutionswhich is very difficult to estimate in the number of FP operations, in the sense that finding such an estimate is itself a nontrivial mathematical problem. And then we, as they say, arrived. How to read FLOPS for a program? There are two ways, both experimental: difficult, giving an accurate result, and easy, but providing a rough estimate. In the first case, we will have to take some basic software implementation of the solution to the problem, compile it into assembler instructions and, having executed them on the processor simulator, calculate the number of FP operations. It sounds so that one wants to go the easy, but unreliable way. Moreover, if the branching of the task execution will depend on the input data, then the entire accuracy of the assessment will immediately be called into question.

The idea of ​​an easy way is as follows. Why not ask the processor how many FP instructions it has completed. The processor pipeline, of course, is unaware of this. But we have performance counters (PMU - here here about them interesting), who can be considered as micro-operations were performed on a particular computer unit. VTune Amplifier XE can work with such counters .

Despite the fact that VTune has many built-in profiles, it does not yet have a special profile for measuring FLOPS. But no one is stopping us from creating our own user profile in 30 seconds. Without bothering you with the basics of working with the VTune interface (you can learn them in the accompanying Getting Started Tutorial), I will immediately describe the process of creating a profile and collecting data.

1. We create a new project and specify our matrix application as the target application .
2. Select the Lightweight Hotspots profile (which uses the Hadware Event-based Sampling processor counter sampling technology) and copy it to create a custom profile. Call it My FLOPS Analysis.
3. We edit the profile, add new processor Sandy Bridge (Events) processor event counters there. We will dwell on them a little more. In their name, executive devices (x87, SSE, AVX) and the type of data on which the operation was performed are encrypted. Each cycle of the processor, the counters add up the number of computational operations assigned for execution. Just in case, we added counters for all possible operations with FP:

• FP_COMP_OPS_EXE. SSE_PACKED_DOUBLE - double precision data vectors (PACKED) (DOUBLE)
• FP_COMP_OPS_EXE. SSE_PACKED_SINGLE - single precision data vectors
• FP_COMP_OPS_EXE. SSE_SCALAR_DOUBLE - scalar DP
• FP_COMP_OPS_EXE. SSE_ SCALAR _SINGLE - scalar SP
• SIMD_FP_256.PACKED_DOUBLE - DP AVX data vectors
• SIMD_FP_256.PACKED_SINGLE - AVX data vectors SP
• FP_COMP_OPS_EXE.x87 - scalar data x87

We can only run the analysis and wait for the results. In the results, we switch to the Hardware Events viewpoint and copy the number of events collected for the multiply3 function : 34,648,000,000.



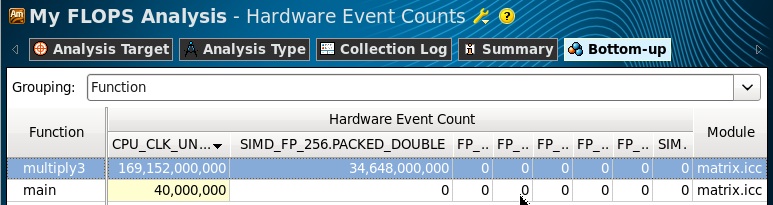
Next, we simply calculate the FLOPS values ​​using the formulas. The data we have been collected for all processors, so multiplication by their number is not required here. Double-precision data operations are performed simultaneously on four 64-bit DP operands in a 256-bit register, so we multiply by a factor of 4. Multiple data with single precision, respectively, by 8. In the last formula, we do not multiply the number of instructions by a factor, since the coprocessor operations x87 are performed only with scalar values. If the program performs several different types of FP operations, then their number multiplied by the coefficients is summed to obtain the resulting FLOPS.

FLOPS = 4 * SIMD_FP_256.PACKED_DOUBLE / Elapsed Time
FLOPS = 8 * SIMD_FP_256.PACKED_SINGLE / Elapsed Time
FLOPS = (FP_COMP_OPS_EXE.x87) / Elapsed Time

Only AVX instructions were executed in our program, therefore, the results contain the value of only one counter SIMD_FP_256.PACKED_DOUBLE.
Make sure that these events are collected for our loop in the multiply3 function (switching to Source View):



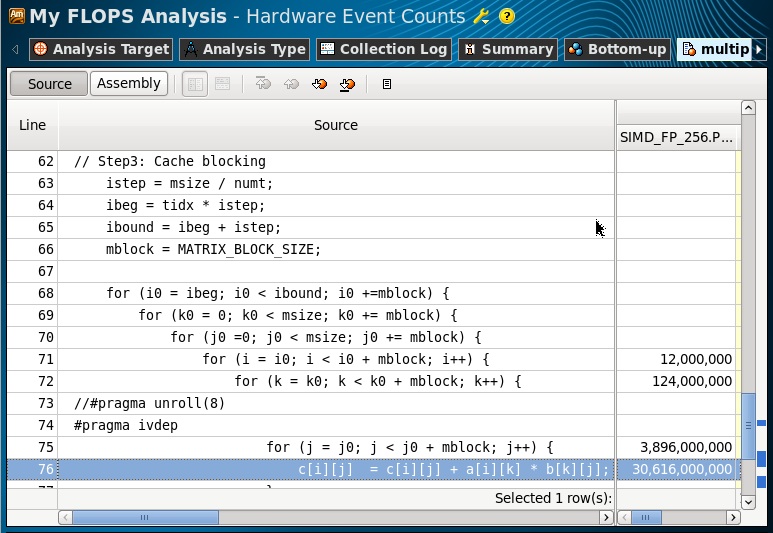
FLOPS = 4 * 34.6Gops / 7s = 19.7 GFlops
The value is consistent with the estimated calculated in the previous paragraph. Therefore, with a sufficient degree of accuracy, we can say that the results of the evaluation method and the measurement coincide. However, there are cases where they may not match. With a certain interest of readers, I can study them and tell how to use more complex and accurate methods. And in return I really want to hear about your cases when you need to measure FLOPS in programs.

Conclusion
FLOPS - a unit of measurement of computing system performance, which characterizes the maximum computing power of the system itself for floating point operations. FLOPS can be declared as theoretical, for systems that do not exist yet, and measured using benchmarks. Developers of high-performance programs, in particular, linear differential equation system solvers, evaluate the performance of their algorithms, including the FLOPS value of the program, calculated using the theoretically / empirically known number of FP operations necessary to execute the algorithm, and the measured test execution time. For cases where the complexity of the algorithm does not allow us to estimate the number of FP operations of the algorithm, they can be measured using performance counters built into Intel microprocessors.