Civilization Springs, 1/5
### Part 1. Golden “Ku”
At six, I fell into the hands of an old-time reference book [50] on trucks from the mid-20th century. The sound, printed on smooth dense paper a rarity. The only thing left in general from the memory of his grandfather after the collapse of the country, wars and crossings.


The handbook contained many interesting TTH, so the word "carrying capacity" became familiar to me from early childhood. And when my father during a walk mentioned that any truck weighs as much as it takes itself, I remembered that. He remembered and, much later, became interested.
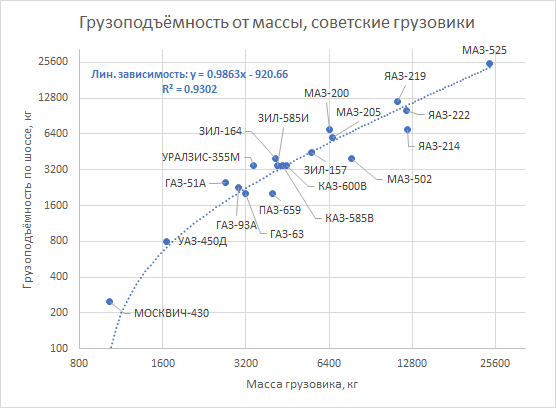
Father was right. For trucks of the 60s, this rule is carried out with rather surprising accuracy:
It is much more curious that this pattern is observed for vehicles completely different from trucks.
At first, for the sake of joke, I plotted cargo planes. And he was surprised. I began to add other vehicles. Riding, floating and flying, built in the centuries 19th, 20th, and 21st, working on thermal energy, nuclear, wind, and even horse. Result? Weak degree and I (index 1.125), if not just a linear dependence. On masses from one hundred kilogram to sixty thousand tons. With deviations, of course, wherever without them, up to 10 times sometimes, but on six orders of the masses, these are obviously trifles.
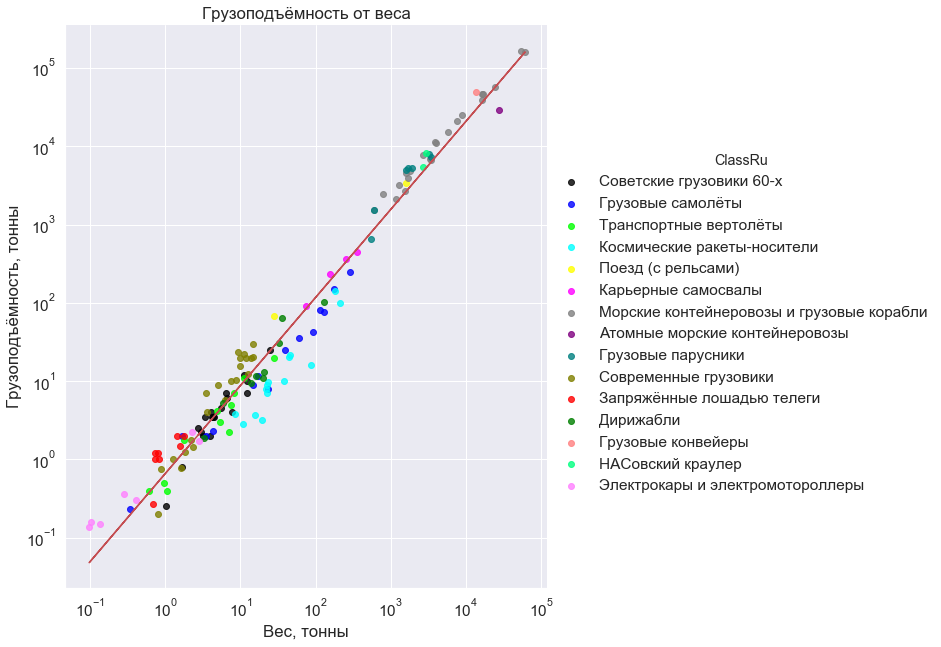
Here it is, this dependence, pressing on the diagonal of an immense empty field:

The graph indicated: cargo aircraft; transport helicopters; airships, modern and the beginning of the century; space launch vehicles (into low orbit); 60s Soviet trucks; modern mining trucks; modern trucks of Russia, USA, China and India; electric cars and cargo scooters; trains (with rails); nuclear container ships; container ships and cargo ships (not tankers); sailing cargo ships of the 17th and 20th centuries; conveyor belts for the transfer of ore; nasovsky tractor for the removal of missiles at the start; and, finally, carts pulled by a horse.
If you enter the value of Q , defined as the mass of the transported cargo in relation to the dry weight of the vehicle, then this is how it looks for each group:

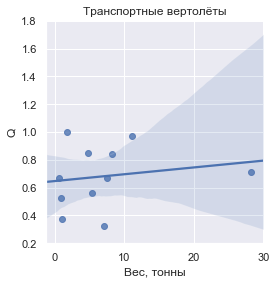

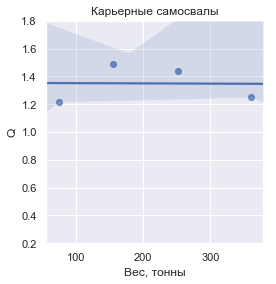




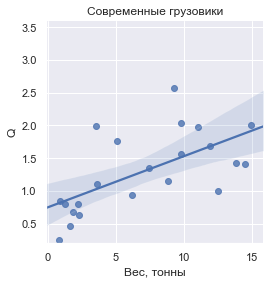


In figures, the values of Q are:
As you can see, Q is not strictly strict , although everywhere, but within the framework of each group, it leads to a common value close to one.
It seemed to me ... mysterious. Why does a wooden sailboat, an aluminum electric car, and a nuclear container ship with a capacity of one hundred thousand electric cars, all raise more or less their weight? What makes us create vehicles with quality Q ≈ 1 on masses that differ thousands of times? Is it a manifestation of the properties of world physics, the terrestrial economy, is this a limitation of human intelligence? How universal is this law, will it be implemented for civilizations from other stars? Global issues. It is unlikely that they will be able to resolve here and now. But to consider and take a glimpse of how much it will turn out, can and should be. This is what we will do.
World Record [ 180 ]lifting barbell man of average weight exceeds 200 kg. Theoretically, this means that our body has a margin of safety for jerk loads up to at least Q = 2.5. However, this requires such unreasonable strengths and training that it is never used in daily activities. It is more expedient to pack sugar into bags of 50 kilograms, although this requires four times more loaders or a walker. Note that this situation is the result of biological evolution, in which the human intellect has (almost) not participated, and therefore has an “alibi” in it.
Physics and engineering in themselves high Qalso do not prohibit. Vaughn, hydrogen turbopump assembly for the main engine of Shuttle, that little thing right in the picture, has an output of 54 MW [ 60 ] at quite automobile weight of 350 kg:

[Image credit: [ 10 ]]
If, simplifying evaluate Q in power on kilogram of mass, it is 100 times higher than that of a decent car. But this thing is almost like a rocket! It is cheaper to make 100 cars with Q = 1 and transport the goods by them, rather than trying to “harness” this unit in a wheeled cart.
Such considerations suggest: the reasons are economic. And not in the narrow sense of specific economies and countries (for our devices are generated by the most diverse peoples and systems), but rather in the sense of “expediency of efforts”. The feasibility is universal enough to, apparently, apply to very different products and somewhere even to animals.
Article written for the site https://habr.com . When copying please refer to the source. The author of the article is Evgeny Bobukh .
Let's try to explore the limits of this expediency quantitatively. We pose the question: how the cost of a device with a fixed mass depends on Q? Here, for example, there is a dump truck weighing 10 tons, taking away 10 tons of cargo. We also want to make 10 tons, but carrying 20 tons ( Q = 2) or even 50 tons ( Q = 5). At the same level of technology development, the same volume of release. It is understood that b of lshie enhance load requirements and the materials (steel -> titanium), and to the motors (other temperature, pressure), and engineering (less tolerance for errors, more clever design). It is clear that with increasing Q everything will be more expensive. But how many times, compared to ten-ton?
This task, of course, is not trivial. Nevertheless, some estimates for it can be obtained from the most general considerations. What we are doing now.
We introduce the function C ( Q). It describes the lowest possible cost of a device with efficiency Q , expressed in the costs of a similar device of the same mass with Q = 1. What is known about it?
1. C (1) = 1, by definition.
2. C ( Q ) is a continuous function, at least until the difference in mass is measured by unit atoms. Intuitively, it seems smooth enough to have the first few derivatives. I think it can be assumed (as with most physical functions) that it is generally analytical.
3. C ( Q ) is a strictly increasing function. The higher Q qualitythe harder it is to make the design, and the more expensive it is. Those. dC ( Q ) / dQ > 0 at least for Q > 0.
4. When Q is greater than about 3 C ( Q ) it starts to increase faster than linearly. Why? Because we see that it is cheaper for people to make three trucks per ten tons with Q = 1 than one at thirty c Q = 3. To summarize, we write: k * C (1) < C ( k ) for k > ≈3 - other In other words, C ( k ) grows faster than k , withk > ≈3.
5. Similarly, since ten aircraft with Q = 0.1 are clearly uneconomical than one with Q = 1 (because they build the second, not the first), then for k > ≈3 we have: k * C (1 / k )> C (1), or C (1 / k )> 1 / k .
6. The cost of the pump from the Shuttle hints that at least up to Q ~ 100 the value of C ( Q ) does not increase as an exponent with a significant figure. Otherwise this THA would cost not millions of dollars, but some $ 10 20 commercial , and we would hardly have done it at all. Those. C(100) is somewhere around 10 3 - 10 8 , but not at all 10 15 .
7. What is C (0)? This is the cost of a device that can still move itself, but is unable to take away any cargo. Obviously, such a "truck" cheaper full. But how many times? History shows that it is rather in times than tens or hundreds. Some 15 years passed from the first aircraft capable of moving only itself ( Q = 0) to the carriage of goods by air. From the first gasoline vehicles to quite decent trucks with Q = 1.5 ([ 120 ] + [ 130]) not much more. If this development were an incredible complexity, it would hardly have ended so quickly. Consequently, the difficulty of manufacture and the cost of a vehicle with Q = 0 should not be completely radically different from that at Q = 1. Hence, we expect that C ( 0 ) is somewhere between 0.1 and 0.5.
8. Does this function make sense with negative Q ? Completely! A truck with Q = -0.5 is one that will budge only if the tower crane "removes" half of its weight from it. A q= -1 is a wagon developing zero thrust. Able to transport cargo only if you take it in tow. That is, without any engine at all. Obviously, its value, if not equal to zero, is very small. Therefore, we set C (-1) ≈ 0.
9. And what is C (-2)? This is the cost of a device that needs to be pulled up with at least twice its weight in order to move! Yes, Q <-1 areas are anchors, foundations, piles, brakes. Devices preventing movement. There, of course, there is a completely different dynamic and its own laws, but at least we see that C ( Q ) does not terminate with a feature for Q <-1, and that in the region of Q= -1 it has a minimum, which means that at least on a small neighborhood of this point C ( Q ) should behave like a parabola.
Thus, the outline of C ( Q ) looks something like this:

We decompose C ( Q ) into a Taylor series at the point Q = -1:
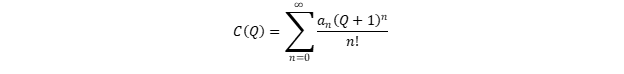
From property (8) it follows that a 0 = 0. Properties (4), (5) and in part (9) they hint that a 1 is close to zero, or in any case that its contribution does not dominate in the range 0 ... 3.
And then it turns out that the first nonzero term in the decomposition of C ( Q ) is parabolic, and that withQ in units of area C ( Q ) behaves approximately as a quadratic function, or a little more rapidly growing:
C ( Q ) ≈ a 2 * ( Q +1) 2 / O 2 + (( Q + 1 ) 3 )
and [1 ] it follows that a 2 ≈ 1/2.
Finally, since at least up to Q ~ 100 the function C ( Q ) is still not exponential (property (6)), then we can put it there equal to Q p with exponent p somewhere in the region of 2 ... 4. Hardly anymore.
Conclusion: For a fixed mass increases not less cost C (Q) device than the (Q + 1) 2 /4, but no faster than about O (Q 4 ) [1]
Whether it is possible to look at real dependence of C ( Q ), to understand how correct this conclusion is? Difficult. Most of the mechanisms manufactured by man are different masses, but fixed Q in the region of one. We also need to the contrary about the same mass, but different the Q . At first I was hoping for data on aircraft engines ... but the work [ 70 ] [ 80 ]their pricing is very funny. Engine prices are classified there, and only prediction formulas and average errors are published.
Fortunately, help came from the passenger cars [ 150 ] . It is with them, at approximately the same mass, that engines of the most different capacities are encountered. And although the power is not yet transported cargo, but with some engineering effort it is roughly proportional to it. What allows us to estimate whether our formula is close to reality.
It seems that yes:

[Source: [ 150 ]]
Blue dots are real cars. In the first approximation, their price increases as the power density to a power of 2.3.
Red dots - the price calculated by the formula [1], based on the assumption thatQ = 1 corresponds to the cheapest cars per kilogram in the range of $ 20-30 thousand. It can be seen that the formula really gives a good estimate of C ( Q ) below (where we were aiming).
When looking at the mass of these tasty points, there is a strong temptation: to lead C ( Q ) through them and, thus, to investigate the dependence directly. You can not do this. Mainly because the price of the car is determined not only by its traction characteristics. It is difficult to imagine a car for a hundred kilobaksov, in which there is no very good conditioner, the most comfortable seats and a “platinum ashtray with rhodium trim”. And all this costs money, not having any relation to our C ( Q). However, the lower “branch” of cars, passing almost exactly according to the calculated C ( Q ), looks interesting. I dare to admit that this is just a car without frills. Where "not checkered, but to go." But about $ 100K more expensive for a car is no longer there.
Article written for the site https://habr.com . When copying please refer to the source. The author of the article is Evgeny Bobukh .
So, we are able to estimate the cost of devices with high Q , at least in order of magnitude. Why was this necessary?
But why? Let's look at the first stage of the space carrier. Well, at least Proton-M [ 110 ], for concreteness. It is almost a full-fledged vehicle, with engines, a control system, a decent safety margin and a dry weight of 31 tons. At the same time at the start of the rocket, it drags on its back not only the payload, but all the fuel, all the upper stages, and, of course, itself. In total - 683 tons. Plus starting overload, total (effectively) 1068 tons of load! From the point of view of the first stage, it works in a creepy mode Q = (1068/31) = 34.4! This is the equivalent of 50 tons of cargo piled on the car.
And we know that the value of the device with a high Q of at least (Q + 1) 2 /4 times higher than something similar with Q≈ 1. For Proton, this is ... 313 times.
That is, “Proton” should cost 300 times more than a similar device with Q = 1. And this figure does not depend much on progress and technology. For as soon as the "British scientists" invent a super-alloy that makes a rocket cheaper, then ground-based engines also become cheaper. Therefore, a chemical rocket, even a reusable one, will always be very expensive. Anyway.
Good. Let's say 300 times. But compared with what ? It would be nice to check our calculations with some objectively existing devices, to avoid gross errors?
Unfortunately, there are no thirty-rockets with Q = 1. But there are approximate analogues suitable for comparison:
It seems that we are not completely divorced from reality.
Let's sum up. Since rockets, even reusable ones, cost 2–3 orders of magnitude more expensive than trucks, any space settlement made of ground-based materials will also cost 100–1,000 times more than a land-based counterpart. This is a very high barrier to development.
Rockets same way because they are very heavy and have to work under unhealthy about in high the Q . But why are rockets heavy? The answer (which is somewhat deeper than the Tsiolkovsky formula) will be considered in the second part.
Continued .
Update: several people tried to point out the ambiguities with regard to fuel when considering rockets. I thought about it. And I realized that the article does have some inaccuracy. Reviewed in the commentshere .

At six, I fell into the hands of an old-time reference book [50] on trucks from the mid-20th century. The sound, printed on smooth dense paper a rarity. The only thing left in general from the memory of his grandfather after the collapse of the country, wars and crossings.


The handbook contained many interesting TTH, so the word "carrying capacity" became familiar to me from early childhood. And when my father during a walk mentioned that any truck weighs as much as it takes itself, I remembered that. He remembered and, much later, became interested.
Father was right. For trucks of the 60s, this rule is carried out with rather surprising accuracy:

It is much more curious that this pattern is observed for vehicles completely different from trucks.
At first, for the sake of joke, I plotted cargo planes. And he was surprised. I began to add other vehicles. Riding, floating and flying, built in the centuries 19th, 20th, and 21st, working on thermal energy, nuclear, wind, and even horse. Result? Weak degree and I (index 1.125), if not just a linear dependence. On masses from one hundred kilogram to sixty thousand tons. With deviations, of course, wherever without them, up to 10 times sometimes, but on six orders of the masses, these are obviously trifles.
Here it is, this dependence, pressing on the diagonal of an immense empty field:

The graph indicated: cargo aircraft; transport helicopters; airships, modern and the beginning of the century; space launch vehicles (into low orbit); 60s Soviet trucks; modern mining trucks; modern trucks of Russia, USA, China and India; electric cars and cargo scooters; trains (with rails); nuclear container ships; container ships and cargo ships (not tankers); sailing cargo ships of the 17th and 20th centuries; conveyor belts for the transfer of ore; nasovsky tractor for the removal of missiles at the start; and, finally, carts pulled by a horse.
If you enter the value of Q , defined as the mass of the transported cargo in relation to the dry weight of the vehicle, then this is how it looks for each group:











In figures, the values of Q are:
| Class of funds | Average Q | Standard deviation q |
| Cargo planes | 0.667091 | ± 0.206162 |
| Transport helicopters | 0.681605 | ± 0.225062 |
| Airships, modern and early century | 0.842673 | ± 0.374622 |
| Space launch vehicles (low orbit) | 0.372446 | ± 0.155810 |
| Soviet trucks of the 60s | 0.777435 | ± 0.232425 |
| Modern Mining Trucks | 1.349610 | ± 0.136840 |
| Modern trucks of Russia, USA, India, China | 1.293679 | ± 0.604313 |
| Electric cards and cargo scooters | 1.098433 | ± 0.343791 |
| Train (with rails) | 2.275989 | ± 0.205999 |
| Nuclear container ships | 1.035233 | ± NA |
| Sea container ships and cargo ships (not tankers) | 2.556004 | ± 0.378040 |
| Sailing cargo ships 17-20 centuries | 2.488461 | ± 0.671785 |
| Cargo conveyor belts | 3.703704 | ± NA |
| Nasovskiy tractor for the launch of rockets | 2.355919 | ± 0.525174 |
| Horse drawn carts | 1.203061 | ± 0.389183 |
As you can see, Q is not strictly strict , although everywhere, but within the framework of each group, it leads to a common value close to one.
How to unit?
Update. Here in the comments a few people expressed bewilderment: what about the unit when we have a three and 0.37 there? The general idea is this: if the carrying capacity and mass were absolutely unrelated, then, dividing the first into the second, we would get a spread of Q values of the commercial data from 10 -5 to 10 5. Очевидно, плюс-минус три раза на фоне этого — пренебрежимо мало, и имеет смысл говорить о «тяготении» к единице и сильной связи параметров. Второй вопрос: а при каком разбросе это уже не имело бы смысла? Краткий ответ: чем ниже разброс значений Q, тем ниже вероятность, что сложившаяся на графике «грузоподъёмность-масса» линейная зависимость — просто случайность. В зависимости от того, какую вероятность этой случайности Вы считаете пренебрежимо малой, Вы получите разные «приемлемые» значения отклонения Q от единицы. Так (я насчитал), при вероятности 10-11 это ±3 раза. При 10-9 это ±10 раз. При 10-8 ±30. При 10-5 ±100 раз. И так далее. Мне лично вероятность ошибки 1 к миллиарду кажется ещё приемлемой, поэтому я готов назвать «близкими к единице» любые Q от 0.1 до 10.
It seemed to me ... mysterious. Why does a wooden sailboat, an aluminum electric car, and a nuclear container ship with a capacity of one hundred thousand electric cars, all raise more or less their weight? What makes us create vehicles with quality Q ≈ 1 on masses that differ thousands of times? Is it a manifestation of the properties of world physics, the terrestrial economy, is this a limitation of human intelligence? How universal is this law, will it be implemented for civilizations from other stars? Global issues. It is unlikely that they will be able to resolve here and now. But to consider and take a glimpse of how much it will turn out, can and should be. This is what we will do.
World Record [ 180 ]lifting barbell man of average weight exceeds 200 kg. Theoretically, this means that our body has a margin of safety for jerk loads up to at least Q = 2.5. However, this requires such unreasonable strengths and training that it is never used in daily activities. It is more expedient to pack sugar into bags of 50 kilograms, although this requires four times more loaders or a walker. Note that this situation is the result of biological evolution, in which the human intellect has (almost) not participated, and therefore has an “alibi” in it.
Physics and engineering in themselves high Qalso do not prohibit. Vaughn, hydrogen turbopump assembly for the main engine of Shuttle, that little thing right in the picture, has an output of 54 MW [ 60 ] at quite automobile weight of 350 kg:

[Image credit: [ 10 ]]
If, simplifying evaluate Q in power on kilogram of mass, it is 100 times higher than that of a decent car. But this thing is almost like a rocket! It is cheaper to make 100 cars with Q = 1 and transport the goods by them, rather than trying to “harness” this unit in a wheeled cart.
Such considerations suggest: the reasons are economic. And not in the narrow sense of specific economies and countries (for our devices are generated by the most diverse peoples and systems), but rather in the sense of “expediency of efforts”. The feasibility is universal enough to, apparently, apply to very different products and somewhere even to animals.
Article written for the site https://habr.com . When copying please refer to the source. The author of the article is Evgeny Bobukh .
Let's try to explore the limits of this expediency quantitatively. We pose the question: how the cost of a device with a fixed mass depends on Q? Here, for example, there is a dump truck weighing 10 tons, taking away 10 tons of cargo. We also want to make 10 tons, but carrying 20 tons ( Q = 2) or even 50 tons ( Q = 5). At the same level of technology development, the same volume of release. It is understood that b of lshie enhance load requirements and the materials (steel -> titanium), and to the motors (other temperature, pressure), and engineering (less tolerance for errors, more clever design). It is clear that with increasing Q everything will be more expensive. But how many times, compared to ten-ton?
This task, of course, is not trivial. Nevertheless, some estimates for it can be obtained from the most general considerations. What we are doing now.
We introduce the function C ( Q). It describes the lowest possible cost of a device with efficiency Q , expressed in the costs of a similar device of the same mass with Q = 1. What is known about it?
1. C (1) = 1, by definition.
2. C ( Q ) is a continuous function, at least until the difference in mass is measured by unit atoms. Intuitively, it seems smooth enough to have the first few derivatives. I think it can be assumed (as with most physical functions) that it is generally analytical.
3. C ( Q ) is a strictly increasing function. The higher Q qualitythe harder it is to make the design, and the more expensive it is. Those. dC ( Q ) / dQ > 0 at least for Q > 0.
4. When Q is greater than about 3 C ( Q ) it starts to increase faster than linearly. Why? Because we see that it is cheaper for people to make three trucks per ten tons with Q = 1 than one at thirty c Q = 3. To summarize, we write: k * C (1) < C ( k ) for k > ≈3 - other In other words, C ( k ) grows faster than k , withk > ≈3.
5. Similarly, since ten aircraft with Q = 0.1 are clearly uneconomical than one with Q = 1 (because they build the second, not the first), then for k > ≈3 we have: k * C (1 / k )> C (1), or C (1 / k )> 1 / k .
6. The cost of the pump from the Shuttle hints that at least up to Q ~ 100 the value of C ( Q ) does not increase as an exponent with a significant figure. Otherwise this THA would cost not millions of dollars, but some $ 10 20 commercial , and we would hardly have done it at all. Those. C(100) is somewhere around 10 3 - 10 8 , but not at all 10 15 .
7. What is C (0)? This is the cost of a device that can still move itself, but is unable to take away any cargo. Obviously, such a "truck" cheaper full. But how many times? History shows that it is rather in times than tens or hundreds. Some 15 years passed from the first aircraft capable of moving only itself ( Q = 0) to the carriage of goods by air. From the first gasoline vehicles to quite decent trucks with Q = 1.5 ([ 120 ] + [ 130]) not much more. If this development were an incredible complexity, it would hardly have ended so quickly. Consequently, the difficulty of manufacture and the cost of a vehicle with Q = 0 should not be completely radically different from that at Q = 1. Hence, we expect that C ( 0 ) is somewhere between 0.1 and 0.5.
8. Does this function make sense with negative Q ? Completely! A truck with Q = -0.5 is one that will budge only if the tower crane "removes" half of its weight from it. A q= -1 is a wagon developing zero thrust. Able to transport cargo only if you take it in tow. That is, without any engine at all. Obviously, its value, if not equal to zero, is very small. Therefore, we set C (-1) ≈ 0.
9. And what is C (-2)? This is the cost of a device that needs to be pulled up with at least twice its weight in order to move! Yes, Q <-1 areas are anchors, foundations, piles, brakes. Devices preventing movement. There, of course, there is a completely different dynamic and its own laws, but at least we see that C ( Q ) does not terminate with a feature for Q <-1, and that in the region of Q= -1 it has a minimum, which means that at least on a small neighborhood of this point C ( Q ) should behave like a parabola.
Thus, the outline of C ( Q ) looks something like this:

We decompose C ( Q ) into a Taylor series at the point Q = -1:
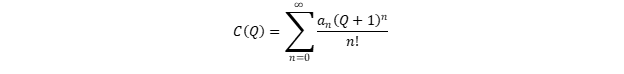
From property (8) it follows that a 0 = 0. Properties (4), (5) and in part (9) they hint that a 1 is close to zero, or in any case that its contribution does not dominate in the range 0 ... 3.
And then it turns out that the first nonzero term in the decomposition of C ( Q ) is parabolic, and that withQ in units of area C ( Q ) behaves approximately as a quadratic function, or a little more rapidly growing:
C ( Q ) ≈ a 2 * ( Q +1) 2 / O 2 + (( Q + 1 ) 3 )
and [1 ] it follows that a 2 ≈ 1/2.
Finally, since at least up to Q ~ 100 the function C ( Q ) is still not exponential (property (6)), then we can put it there equal to Q p with exponent p somewhere in the region of 2 ... 4. Hardly anymore.
Conclusion: For a fixed mass increases not less cost C (Q) device than the (Q + 1) 2 /4, but no faster than about O (Q 4 ) [1]
Whether it is possible to look at real dependence of C ( Q ), to understand how correct this conclusion is? Difficult. Most of the mechanisms manufactured by man are different masses, but fixed Q in the region of one. We also need to the contrary about the same mass, but different the Q . At first I was hoping for data on aircraft engines ... but the work [ 70 ] [ 80 ]their pricing is very funny. Engine prices are classified there, and only prediction formulas and average errors are published.
Fortunately, help came from the passenger cars [ 150 ] . It is with them, at approximately the same mass, that engines of the most different capacities are encountered. And although the power is not yet transported cargo, but with some engineering effort it is roughly proportional to it. What allows us to estimate whether our formula is close to reality.
It seems that yes:

[Source: [ 150 ]]
Blue dots are real cars. In the first approximation, their price increases as the power density to a power of 2.3.
Red dots - the price calculated by the formula [1], based on the assumption thatQ = 1 corresponds to the cheapest cars per kilogram in the range of $ 20-30 thousand. It can be seen that the formula really gives a good estimate of C ( Q ) below (where we were aiming).
When looking at the mass of these tasty points, there is a strong temptation: to lead C ( Q ) through them and, thus, to investigate the dependence directly. You can not do this. Mainly because the price of the car is determined not only by its traction characteristics. It is difficult to imagine a car for a hundred kilobaksov, in which there is no very good conditioner, the most comfortable seats and a “platinum ashtray with rhodium trim”. And all this costs money, not having any relation to our C ( Q). However, the lower “branch” of cars, passing almost exactly according to the calculated C ( Q ), looks interesting. I dare to admit that this is just a car without frills. Where "not checkered, but to go." But about $ 100K more expensive for a car is no longer there.
Article written for the site https://habr.com . When copying please refer to the source. The author of the article is Evgeny Bobukh .
So, we are able to estimate the cost of devices with high Q , at least in order of magnitude. Why was this necessary?
But why? Let's look at the first stage of the space carrier. Well, at least Proton-M [ 110 ], for concreteness. It is almost a full-fledged vehicle, with engines, a control system, a decent safety margin and a dry weight of 31 tons. At the same time at the start of the rocket, it drags on its back not only the payload, but all the fuel, all the upper stages, and, of course, itself. In total - 683 tons. Plus starting overload, total (effectively) 1068 tons of load! From the point of view of the first stage, it works in a creepy mode Q = (1068/31) = 34.4! This is the equivalent of 50 tons of cargo piled on the car.
And we know that the value of the device with a high Q of at least (Q + 1) 2 /4 times higher than something similar with Q≈ 1. For Proton, this is ... 313 times.
That is, “Proton” should cost 300 times more than a similar device with Q = 1. And this figure does not depend much on progress and technology. For as soon as the "British scientists" invent a super-alloy that makes a rocket cheaper, then ground-based engines also become cheaper. Therefore, a chemical rocket, even a reusable one, will always be very expensive. Anyway.
Good. Let's say 300 times. But compared with what ? It would be nice to check our calculations with some objectively existing devices, to avoid gross errors?
Unfortunately, there are no thirty-rockets with Q = 1. But there are approximate analogues suitable for comparison:
- The very first one is a mining truck. Yes, not a rocket. But still, too, the heat engine, not quite a trivial engineering, and one of the cheapest means for the transport of goods. And if we are talking about space exploration, shouldn't a truck be a prototype of the business model of a space cab driver? So we will try, at least for the general estimation. Here is a 30-ton BelAZ-7540. The market price [ 140 ] is 3.7 million rubles, i.e. $ 62K. For Proton, this is converted into the cost of the first stage in the region of $ 19 million. Wikipedia stands for [ 100 ] launch costs as $ 65 million. Pretty close, considering that this amount includes a lot more, except for the price of the very first step.
- An experimental rocket platform on rails is described in [ 160 ]. Mass under 10 tons, five steps, accelerates to 4 km / s. Price 750 kilobaksov. Judging by the published pictures and parameters, this device works somewhere at Q = 10. Not one, but still not 34. If we start from these numbers, the first step of Proton should cost somewhere around $ 23 million.
- Generally, when I try to imagine a rocket with Q = 1, in front of my mind there is such a hefty disc with a small hollow filled with gunpowder. Gunpowder burns out and pushes the pig forward. Quite a bit, so much you will not overclock. I spent two days redeeming this picture until I realized what it reminds me of. This is ... a pneumatic hammer! Where gas expands and pushes the disc. Ultimate bastardization of the idea of a jet engine, still retaining some kind of kinship. Well, we are looking for. Yeah, here is [ 170 ] the Stanko M212 air hammer. The weight of the blank is 2 tons, the whole structure is 58.3 tons. The Q system, therefore, is a modest 0.034. Sold for 40 thousand euros. If you extrapolate the cost of this joke on Q= 34.4 according to the formula [1], it turns out ... 47 million euros. Or 24 million in a proportion of 30 tons.
It seems that we are not completely divorced from reality.
Let's sum up. Since rockets, even reusable ones, cost 2–3 orders of magnitude more expensive than trucks, any space settlement made of ground-based materials will also cost 100–1,000 times more than a land-based counterpart. This is a very high barrier to development.
Rockets same way because they are very heavy and have to work under unhealthy about in high the Q . But why are rockets heavy? The answer (which is somewhat deeper than the Tsiolkovsky formula) will be considered in the second part.
Continued .
Update: several people tried to point out the ambiguities with regard to fuel when considering rockets. I thought about it. And I realized that the article does have some inaccuracy. Reviewed in the commentshere .
About the data
Желающие самостоятельно проанализировать данные могут найти их (вместе с источниками) здесь в формате CSV. (Кстати, какие на Хабре есть лучшие варианты, кроме выкладывания файла на сторонний хостинг?) При работе с ними следует учесть следующее.
1. Рассматривались только грузовые транспортные средства. Пассажирская Тесла с вместимостью багажника в 70 кг — не грузовик. Грузовые фургоны тоже (почти) исключены — у них средства защиты груза вносят существенные искажения.
2. С советскими грузовиками работать было одно удовольствие. Вот вес, вот допустимая нагрузка, всё чётко. С современными, особенно американскими — беда. Мало кто публикует их максимальную грузоподъёмность. Вместо этого есть законы, разрешающие ту или иную нагрузку для каждого типа бизнеса и дорог. Плюс приписка к грузовику: «удовлетворяет стандарту № такой-то, § такой-то». Полная, разгромная победа бюрократии над физической реальностью. В тех случаях, когда грузоподъёмность всё-таки публикуется, она сплошь и рядом взятаот балды из маркетинговых соображений. Строишь график — а там явная «ёлочка», пардон, линейка продуктов. По этой причине, увы, данные современных грузовиков более зашумлены (± 0.60), нежели старых (± 0.23). Положение отчасти спасли Китай, Россия и Индия: у них ТТХ грузовиков по-прежнему легкодоступны.
3. Самые лёгкие электрические кары и мотоциклы весят зачастую по 30-70 кг, перевозя при этом по 200-400 кг груза. На первый взгляд, это выглядит как Q в районе десятки. Но я подумал и кое-что осознал. Все эти транспортные средства не ездят без человека. Более того, человек в них выполняет ещё и структурно-силовую и балансирующую роль. Он в них — не полезная нагрузка, без которой можно и уехать, а неотъемлемая запчасть. Поэтому и массу их надо считать с водителем (+80 кг). А это уже 100-150 кг. Аналогичная поправка вносилась в характеристики конных экипажей, с массой лошади принятой за 500 кг.
4. Массу поезда я считал с массой подстилающих его рельсов. Ибо, в отличие от прочих транспортных средств, перемещаться поезд может только по рельсам, а они весят существенно и держат транспортную нагрузку. Как гусеницы у бульдозера. Только не носимые с собой. При этом на сами рельсы, вагоны и электровозы существует куча запутанных спецификаций, в которых я не факт, что правильно разобрался.
5. Атомный грузовой ледокол в мире один: российский Севморпуть[600], так что и точка в этой группе лишь одна.
6. С грузовыми мореходными судами тоже не всё просто. Для большинства из них не публикуется ни максимальная масса груза, ни пустая масса конструкции. Для второго, правда, есть всё-таки термин: LWT — Light Weight Tonnage, и его значения изредка встречается на корабельных аукционах (типа [610] и [620]). Долгим ручным вычитыванием этих сайтов я надёргал цифр по LWT, но как быть с перевозимым грузом? Вместо него обычно используется величина DWT (Deadweight Tonnage), представляющая собой полный максимально возможный вес корабля. В который входят не только вес груза, но и конструкции, топлива, вспомогательных жидкостей, и ещё каких-то мелочей. Пошарившись по разным сайтам, я установил, что на практике предельный вес груза обычно составляет 85% от (DWT — LWT), с разбросом в 65-90%. Этим пришлось и удовлетвориться. Так что грузоподъёмность считалась как Г = 0.85*(DWT — LWT). Что, возможно, внесло погрешность до 30%.
7. По космическим носителям я опирался в основном на [110]. Там лежит разбивка многих ракет по ступеням и их массам. К сожалению, иногда с пометкой, что масса ступени включает остатки несгоревшего топлива, которые толком неизвестны. По этой причине величина Q для ракет, возможно, занижена процентов на 10.
8. Были ли транспортные средства, в эту картину не вписывающиеся? Конечно. Во-первых, негрузовые. Танки. Пассажирские автомобили, круизные пароходы. У них Q существенно меньше единицы. С последними всё понятно: их цель — не груз увезти, а людей, да ещё с комфортом. Вес средств комфорта портит им картину. Во-вторых, сюда не вписываются танкеры, у которых Q нередко достигает 3-8 единиц. Но у танкеров особенный и очень «удобный» груз, допускающий равномерное распределение нагрузки по корпусу и удержание её не столько собственной прочностью, сколько внешним давлением моря. На суше аналогом этого был бы грузовик с «костылями», но таких нет, сравнивать не с чем, а потому танкеры я на графике не указал (хотя вот упоминаю здесь).
Желающие самостоятельно проанализировать данные могут найти их (вместе с источниками) здесь в формате CSV. (Кстати, какие на Хабре есть лучшие варианты, кроме выкладывания файла на сторонний хостинг?) При работе с ними следует учесть следующее.
1. Рассматривались только грузовые транспортные средства. Пассажирская Тесла с вместимостью багажника в 70 кг — не грузовик. Грузовые фургоны тоже (почти) исключены — у них средства защиты груза вносят существенные искажения.
2. С советскими грузовиками работать было одно удовольствие. Вот вес, вот допустимая нагрузка, всё чётко. С современными, особенно американскими — беда. Мало кто публикует их максимальную грузоподъёмность. Вместо этого есть законы, разрешающие ту или иную нагрузку для каждого типа бизнеса и дорог. Плюс приписка к грузовику: «удовлетворяет стандарту № такой-то, § такой-то». Полная, разгромная победа бюрократии над физической реальностью. В тех случаях, когда грузоподъёмность всё-таки публикуется, она сплошь и рядом взята
3. Самые лёгкие электрические кары и мотоциклы весят зачастую по 30-70 кг, перевозя при этом по 200-400 кг груза. На первый взгляд, это выглядит как Q в районе десятки. Но я подумал и кое-что осознал. Все эти транспортные средства не ездят без человека. Более того, человек в них выполняет ещё и структурно-силовую и балансирующую роль. Он в них — не полезная нагрузка, без которой можно и уехать, а неотъемлемая запчасть. Поэтому и массу их надо считать с водителем (+80 кг). А это уже 100-150 кг. Аналогичная поправка вносилась в характеристики конных экипажей, с массой лошади принятой за 500 кг.
4. Массу поезда я считал с массой подстилающих его рельсов. Ибо, в отличие от прочих транспортных средств, перемещаться поезд может только по рельсам, а они весят существенно и держат транспортную нагрузку. Как гусеницы у бульдозера. Только не носимые с собой. При этом на сами рельсы, вагоны и электровозы существует куча запутанных спецификаций, в которых я не факт, что правильно разобрался.
5. Атомный грузовой ледокол в мире один: российский Севморпуть[600], так что и точка в этой группе лишь одна.
6. С грузовыми мореходными судами тоже не всё просто. Для большинства из них не публикуется ни максимальная масса груза, ни пустая масса конструкции. Для второго, правда, есть всё-таки термин: LWT — Light Weight Tonnage, и его значения изредка встречается на корабельных аукционах (типа [610] и [620]). Долгим ручным вычитыванием этих сайтов я надёргал цифр по LWT, но как быть с перевозимым грузом? Вместо него обычно используется величина DWT (Deadweight Tonnage), представляющая собой полный максимально возможный вес корабля. В который входят не только вес груза, но и конструкции, топлива, вспомогательных жидкостей, и ещё каких-то мелочей. Пошарившись по разным сайтам, я установил, что на практике предельный вес груза обычно составляет 85% от (DWT — LWT), с разбросом в 65-90%. Этим пришлось и удовлетвориться. Так что грузоподъёмность считалась как Г = 0.85*(DWT — LWT). Что, возможно, внесло погрешность до 30%.
7. По космическим носителям я опирался в основном на [110]. Там лежит разбивка многих ракет по ступеням и их массам. К сожалению, иногда с пометкой, что масса ступени включает остатки несгоревшего топлива, которые толком неизвестны. По этой причине величина Q для ракет, возможно, занижена процентов на 10.
8. Были ли транспортные средства, в эту картину не вписывающиеся? Конечно. Во-первых, негрузовые. Танки. Пассажирские автомобили, круизные пароходы. У них Q существенно меньше единицы. С последними всё понятно: их цель — не груз увезти, а людей, да ещё с комфортом. Вес средств комфорта портит им картину. Во-вторых, сюда не вписываются танкеры, у которых Q нередко достигает 3-8 единиц. Но у танкеров особенный и очень «удобный» груз, допускающий равномерное распределение нагрузки по корпусу и удержание её не столько собственной прочностью, сколько внешним давлением моря. На суше аналогом этого был бы грузовик с «костылями», но таких нет, сравнивать не с чем, а потому танкеры я на графике не указал (хотя вот упоминаю здесь).
Links
[10] Схема SSME: http://www.jht.com/icuf/Space-Science/LiquidRockets/PT-04-125.htm
[50] А. П. Рунова, А. А. Вагнер. ГРУЗОВЫЕ АВТОМОБИЛИ. КАТАЛОГ. Типография ЦИНТИМАШ, 1960 г.
[60] Power-to-weight ratios: https://en.wikipedia.org/wiki/Power-to-weight_ratio#Heat_engines_and_heat_pumps
[70] Development and Production Cost Estimating Relationships for Aircraft Turbine Engines by John Birkler, Jeffrey B. Garfinkle, Kenneth E. Marks, https://www.rand.org/content/dam/rand/pubs/notes/2005/N1882.pdf
[80] Military Jet Engine Acquisition (Technology Basics and Cost-Estimating Methodology), Obaid Younossi, Mark V. Arena, Richard M. Moore
Mark Lorell, Joanna Mason, John C. Graser, https://www.rand.org/content/dam/rand/pubs/monograph_reports/2005/MR1596.pdf
[100] Стоимость пуска Протона-М: https://en.wikipedia.org/wiki/Proton-M
[110] Данные по ступеням «Протона»: http://www.spacelaunchreport.com/proton.html
[120] Ford TT curb weight: https://www.conceptcarz.com/s13963/ford-model-tt-type-c.aspx
[130] Ford TT load capacity: https://en.wikipedia.org/wiki/Ford_Model_TT
[140] Цена на Белаз-7540: http://www.raise.ru/market/mining/haul-trucks/id-market_43697/
[150] Подборка ста с лишним автомобилей с данными по мощности, весу, цене, и удельным параметрам: https://oppositelock.kinja.com/whats-the-best-power-weight-ratio-per-dollar-1699756090 (автор проделал нетривиальную работу, но почему-то гадает, нужны ли эти данные. Да ещё как нужны!)
[160] Ракетные сани: http://www.impactlab.net/2006/01/15/the-fastest-rocket-sled-on-earth/
[170] Пневматический молот https://www.machineseeker.com/Air-steam-Forging-Hammer-double-action-Stanko-M212-RAM-2000kg/i-3521173
[180] Мировые рекорды в тяжёлой атлетике: https://ru.wikipedia.org/wiki/%D0%9C%D0%B8%D1%80%D0%BE%D0%B2%D1%8B%D0%B5_%D1%80%D0%B5%D0%BA%D0%BE%D1%80%D0%B4%D1%8B_%D0%B2_%D1%82%D1%8F%D0%B6%D1%91%D0%BB%D0%BE%D0%B9_%D0%B0%D1%82%D0%BB%D0%B5%D1%82%D0%B8%D0%BA%D0%B5
[10] Схема SSME: http://www.jht.com/icuf/Space-Science/LiquidRockets/PT-04-125.htm
[50] А. П. Рунова, А. А. Вагнер. ГРУЗОВЫЕ АВТОМОБИЛИ. КАТАЛОГ. Типография ЦИНТИМАШ, 1960 г.
[60] Power-to-weight ratios: https://en.wikipedia.org/wiki/Power-to-weight_ratio#Heat_engines_and_heat_pumps
[70] Development and Production Cost Estimating Relationships for Aircraft Turbine Engines by John Birkler, Jeffrey B. Garfinkle, Kenneth E. Marks, https://www.rand.org/content/dam/rand/pubs/notes/2005/N1882.pdf
[80] Military Jet Engine Acquisition (Technology Basics and Cost-Estimating Methodology), Obaid Younossi, Mark V. Arena, Richard M. Moore
Mark Lorell, Joanna Mason, John C. Graser, https://www.rand.org/content/dam/rand/pubs/monograph_reports/2005/MR1596.pdf
[100] Стоимость пуска Протона-М: https://en.wikipedia.org/wiki/Proton-M
[110] Данные по ступеням «Протона»: http://www.spacelaunchreport.com/proton.html
[120] Ford TT curb weight: https://www.conceptcarz.com/s13963/ford-model-tt-type-c.aspx
[130] Ford TT load capacity: https://en.wikipedia.org/wiki/Ford_Model_TT
[140] Цена на Белаз-7540: http://www.raise.ru/market/mining/haul-trucks/id-market_43697/
[150] Подборка ста с лишним автомобилей с данными по мощности, весу, цене, и удельным параметрам: https://oppositelock.kinja.com/whats-the-best-power-weight-ratio-per-dollar-1699756090 (автор проделал нетривиальную работу, но почему-то гадает, нужны ли эти данные. Да ещё как нужны!)
[160] Ракетные сани: http://www.impactlab.net/2006/01/15/the-fastest-rocket-sled-on-earth/
[170] Пневматический молот https://www.machineseeker.com/Air-steam-Forging-Hammer-double-action-Stanko-M212-RAM-2000kg/i-3521173
[180] Мировые рекорды в тяжёлой атлетике: https://ru.wikipedia.org/wiki/%D0%9C%D0%B8%D1%80%D0%BE%D0%B2%D1%8B%D0%B5_%D1%80%D0%B5%D0%BA%D0%BE%D1%80%D0%B4%D1%8B_%D0%B2_%D1%82%D1%8F%D0%B6%D1%91%D0%BB%D0%BE%D0%B9_%D0%B0%D1%82%D0%BB%D0%B5%D1%82%D0%B8%D0%BA%D0%B5
[600] Севморпуть, советское ледокольно-транспортное судно (лихтеровоз) с атомной силовой установкой: https://ru.wikipedia.org/wiki/Севморпуть_(лихтеровоз)
[610] Доска объявлений по продаже кораблей: http://www.seaboats.net
[620] Доска объявлений по продаже кораблей: http://www.vedshipping.com
