Algorithms LZW, LZ77 and LZ78

I would like to continue my previous topic about compression algorithms . This time I will talk about the LZW algorithm and a little about its relatives, the LZ77 and LZ78 algorithms.

LZW Algorithm

The Lempel-Ziv-Welch (LZW) algorithm is a universal lossless data compression algorithm.

The immediate predecessor of LZW was the LZ78 algorithm, published by Abraham Lempel and Jacob Ziv in 1978. This algorithm was perceived as a mathematical abstraction until 1984, when Terry A. Welch published his work with a modified the algorithm, later called LZW (Lempel-Ziv-Welch).

Description

The compression process is as follows. The characters of the input stream are sequentially read and a check is made to see if such a line exists in the created row table. If such a line exists, the next character is read, and if the line does not exist, the code for the previous found line is entered into the stream, the line is entered into the table, and the search starts again.
For example, if byte data (text) is compressed, then the rows in the table will be 256 (from “0” to “255”). If a 10-bit code is used, then under the codes for the rows, values ​​remain in the range from 256 to 1023. New rows form the table sequentially, that is, the row index can be considered its code.
The input decoding algorithm only requires encoded text, since it can recreate the corresponding conversion table directly from the encoded text. The algorithm generates a uniquely decoded code due to the fact that every time a new code is generated, a new row is added to the row table. LZW constantly checks to see if the string is already known, and, if so, displays the existing code without generating a new one. Thus, each line will be stored in a single copy and have its own unique number. Therefore, when decrypting, when a new code is received, a new line is generated, and when it is already known, a line is extracted from the dictionary.

Algorithm Pseudocode

1. Initialization of the dictionary with all possible single-character phrases. Initialization of the input phrase ω by the first character of the message.
2. Read the next character K from the encoded message.
3. If END MESSAGES, then issue the code for ω, otherwise:
4. If the phrase ω (K) is already in the dictionary, assign the value ω (K) to the input phrase and go to Step 2, otherwise output the code ω, add ω (K) to the dictionary, assign the value K to the input phrase and go to Step 2.
5. the end

Example

It’s just that it’s not very easy to understand the operation of the algorithm using pseudo-code, so let’s look at it. Consider an example of image compression and decoding.
First, create an initial dictionary of single characters. There are 256 different characters in the standard ASCII encoding, therefore, in order for all of them to be correctly encoded (if we do not know which characters will be present in the source file and which will not), the initial code size will be 8 bits. If we know in advance that there will be fewer different characters in the source file, then it is quite reasonable to reduce the number of bits. To initialize the table, we will establish the correspondence of code 0 to the corresponding character with bit code 00000000, then 1 corresponds to the character with code 00000001, etc., up to code 255. In fact, we indicated that each code from 0 to 255 is the root.
There will no longer be other codes in the table that have this property.
As the dictionary grows, the size of the groups must grow in order to take into account new elements. 8-bit groups give 256 possible combinations of bits, so when the 256th word appears in the dictionary, the algorithm should go to 9-bit groups. When the 512th word appears, a transition to 10-bit groups will occur, which makes it possible to remember already 1024 words, etc.
In our example, the algorithm knows in advance that only 5 different characters will be used, therefore, the minimum number of bits will be used to store them, allowing us to remember them, that is 3 (8 different combinations).

Coding

Let us compress the sequence “abacabadabacabae”.

• Step 1: Then, according to the above algorithm, we will add “a” to the initially empty row and check if row “a” is in the table. Since during initialization we entered all the rows of one character into the table, the row “a” is in the table.
• Step 2: Next, we read the next character “b” from the input stream and check if there is a string “ab” in the table. There is no such row in the table yet.
• Add to the table <5> “ab”. To stream: <0>;
• Step 3: “ba” - no. To table: <6> “ba”. To stream: <1>;
• Step 4: “ac” is not. To table: <7> “ac”. To stream: <0>;
• Step 5: “ca” - no. To table: <8> “ca”. To stream: <2>;
• Step 6: “ab” - is in the table; “Aba” is not. To table: <9> “aba”. To stream: <5>;
• Step 7: “ad” - no. To table: <10> “ad”. To stream: <0>;
• Step 8: “da” - no. To table: <11> “da”. To stream: <3>;
• Step 9: “aba” - is in the table; “Abac” is not. To table: <12> “abac”. To stream: <9>;
• Step 10: “ca” - is in the table; “Cab” - no. To table: <13> “cab”. To stream: <8>;
• Step 11: “ba” - is in the table; “Bae” is not. To table: <14> “bae”. To stream: <6>;
• Step 12: And finally, the last line “e”, followed by the end of the message, so we simply output to stream <4>.

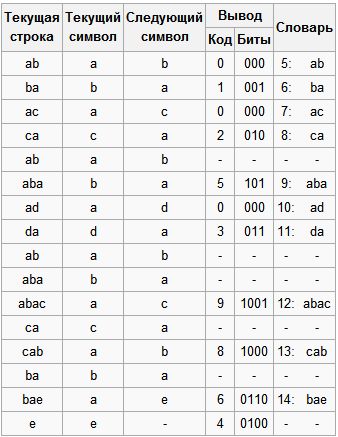
So, we get the encoded message "0 1 0 2 5 0 3 9 8 6 4", which is 11 bits shorter.

Decoding

The peculiarity of LZW is that for decompression we do not need to save the table of lines in a file for unpacking. The algorithm is constructed in such a way that we are able to restore the table of rows using only a stream of codes.
Now imagine that we have received the encoded message above, and we need to decode it. First of all, we need to know the initial dictionary, and we can reconstruct subsequent entries in the dictionary on the go, since they are just a concatenation of previous entries.

Addition

To increase the degree of image compression using this method, one “trick” of implementing this algorithm is often used. Some files that are compressed using LZW have frequently occurring strings of identical characters, for example aaaaaa ... or 30, 30, 30 ... etc. Their direct compression will generate output code 0, 0, 5, etc. The question is, is it possible to increase the compression ratio in this particular case?
It turns out that this is possible if we stipulate some actions:
We know that for each code we need to add to the table a line consisting of a line already present there and a character with which the next line in the stream begins.

• So, the encoder puts the first “a” in the string, searches and finds the “a” in the dictionary. Adds the following “a” to the line, finds that “aa” is not in the dictionary. Then he adds the entry <5>: "aa" to the dictionary and displays the label <0> ("a") in the output stream.
• Then the line is initialized by the second “a”, that is, it takes the form “a?” The third “a” is entered, the line is again equal to “aa”, which is now in the dictionary.
• If the fourth “a” appears, then the line “aa?” Is equal to “aaa”, which is not in the dictionary. The dictionary is updated with this line, and the output is marked <5> ("aa").
• After that, the line is initialized by the third "a", etc. etc. The further process is quite clear.
• As a result, we get the sequence 0, 5, 6 ..., which is shorter than direct coding using the standard LZW method.

It can be shown that such a sequence will be correctly restored. The decoder first reads the first code - this is <0>, which corresponds to the character "a". Then it reads the code <5>, but this code is not in its table. But we already know that such a situation is possible only if the added character is equal to the first character of the sequence just read, that is, “a”. Therefore, he will add the string “aa” with the code <5> to his table, and put “aa” in the output stream. And so the whole chain of codes can be decoded.
Moreover, we can apply the coding rule described above in the general case not only to consecutive identical characters, but also to sequences in which the next added character is equal to the first character of the chain.

Advantages and disadvantages

+ Does not require calculation of probabilities of occurrence of characters or codes.
+ For decompression it is not necessary to save the table of lines in a file for unpacking. The algorithm is constructed in such a way that we are able to restore the table of rows using only a stream of codes.
+ This type of compression does not distort the original image file, and is suitable for compressing any type of raster data.
- The algorithm does not analyze the input data, therefore, is not optimal.

Application

The publication of the LZW algorithm made a great impression on all information compression specialists. This was followed by a large number of programs and applications with various variations of this method.
This method allows you to achieve one of the best compression ratios among other existing methods for compressing graphic data, in the complete absence of loss or distortion in the source files. It is currently used in TIFF, PDF, GIF, PostScript and other files, as well as partly in many popular data compression programs (ZIP, ARJ, LHA).

Algorithms LZ77 and LZ78

LZ77 and LZ78 are lossless compression algorithms published by Abraham Lempel and Jacob Ziv in 1977 and 1978. These algorithms are best known in the LZ * family, which also includes LZW, LZSS, LZMA and other algorithms. Both algorithms relate to vocabulary-based algorithms. The LZ77 uses the so-called “sliding window”, which is equivalent to the implicit use of the vocabulary approach first proposed in LZ78.

Principle of Operation LZ77

The main idea of ​​the algorithm is to replace the repeated occurrence of the string with a link to one of the previous entry positions. To do this, use the sliding window method. A sliding window can be represented in the form of a dynamic data structure, which is organized in such a way as to memorize the “said” information earlier and provide access to it. Thus, the compression coding process according to LZ77 is reminiscent of writing a program whose commands allow you to access the elements of a sliding window, and instead of the values ​​of the compressed sequence, insert links to these values ​​in the sliding window. In the standard LZ77 algorithm, string matches are encoded by a pair:

• match length
• offset or distance

The encoded pair is treated precisely as a command to copy characters from a sliding window from a certain position, or literally as: “Return to the dictionary the value of the offset characters and copy the value of the length of the characters, starting from the current position. A feature of this compression algorithm is that the use of the encoded length-offset pair is not only acceptable, but also effective in cases where the length value exceeds the offset value. The example with the copy command is not entirely obvious: “Go back 1 character in the buffer and copy 7 characters starting from the current position.” How can I copy 7 characters from the buffer when only 1 character is currently in the buffer? However, the following interpretation of the coding pair may clarify the situation: every 7 subsequent characters match (equivalent) with 1 character in front of them. This means that each character can be uniquely determined by moving back in the buffer, even if this character is not yet in the buffer at the time of decoding the current length-offset pair.

Algorithm description

LZ77 uses a message-sliding window. Suppose the window is locked at the current iteration. On the right side of the window, we expand the substring while it is in the line <sliding window + expandable line> and starts in the sliding window. We call the stackable string buffer. After building up, the algorithm produces a code consisting of three elements:

• offset in the window;
• buffer length;
• last character of the buffer.

At the end of the iteration, the algorithm shifts the window by a length equal to the length of the buffer + 1.

Kabababababz example

Description of Algorithm LZ78

Unlike LZ77, which works with already received data, LZ78 focuses on data that will only be received (LZ78 does not use a sliding window, it stores a dictionary of already viewed phrases). The algorithm reads the message characters until the accumulated substring is included entirely in one of the dictionary phrases. As soon as this line no longer matches at least one phrase of the dictionary, the algorithm generates a code consisting of the index of the line in the dictionary, which until the last character entered contained the input line, and the character that violated the match. Then, the entered substring is added to the dictionary. If the dictionary is already filled, then the phrase used in comparisons is previously deleted from it. If at the end of the algorithm we don’t find the symbol that violated the matches,

Kabababababz example