Dynamic programming method for counting the number of cycles on a rectangular lattice
This article is addressed to those readers who are engaged in programming algorithms, and are especially interested in hard-to-solve problems. Those habrahlyudy who against placement of algorithms on Habr should immediately stop reading this work.
In the article I will show how to use the dynamic programming method for the profile to solve the problem of counting the number of Hamiltonian cycles on a rectangular lattice of size m by n. On Habré there are several articles devoted to the topic of dynamic programming (for example, this one ), but nowhere is it a question of a more complex application of the method. This approach can also be called the transfer matrix method, as you like.
I warn you that the article contains about 2,000 words (8 A4 pages), but the one who walks will overcome the road.
What is a difficult task? This is a task that does not have an effective solution algorithm. Moreover, this is not necessarily a problem with the exponential complexity of the solution, the complexity can be polynomial, but with a sufficiently large degree of polynomial (for example, the problem of k queens, which I already wrote about here ). More about such problems and their classification can be found in the classic book by M. Gary, D. Johnson, “Computing machines and hard-to-solve problems.”
Such problems are usually solved by brute force, dynamic programming, and combinatorial analysis. Often an acceptable solution is obtained by using these three components at the same time, but this also requires experience in writing fairly optimal code. It’s very good if you have at hand a cluster of at least several thousand cores and at least a couple of hundred gigabytes of RAM. Unfortunately, I’m not joking, many problems can be solved only on such a machine ...
I like to solve difficult problems and from time to time I organize competitions for mathematicians-programmers on this subject. This article is partly dedicated to the Pre-Hamiltonian Cycles contest.”, Which began on October 1 and ends on October 31, 2010. The task proposed in the conditions of the competition is solved by me in the same way (with minor changes), which will be described here.
In the section with the derivation of the complexity of the algorithm, it is assumed that the reader knows the elements of combinatorics (what is the number of combinations, for example), and in the section on the finite state machine, the reader will be forced to recall elements of graph theory (for example, what is the adjacency matrix of a graph, and what gives its construction in power).
In this work, we encounter a graph called a rectangular lattice P m × P n . A rectangular lattice is an integer point on the coordinate plane, connected by the principle of closest proximity. The notation P m × P n is due to the fact that an integer rectangle is a direct product of two chains, the first of which has m links (denoted by P m ), and the second by n (denoted by P n ). The number m is the width of the lattice (length from left to right), and n is its length (length from bottom to top).
A Hamiltonian cycle in a graph is a cycle passing through each vertex exactly once. In fig. Figure 1 shows an example of a Hamiltonian cycle on the lattice P 6 × P8 .

Figure 1 - An example of a Hamiltonian cycle on a 6 × 8 lattice
The task is to find the number of Hamiltonian cycles on a lattice P m × P n for given m, n ≥ 2 . For example, the following figure shows all 6 Hamiltonian cycles on a 4 × 4 lattice.

Figure 2 - All 6 Hamiltonian cycles on a 4 × 4 lattice
Any cycle in the graph P m × P n can be built sequentially on the “layers” P m × P k (k = 0,1,2, ..., n). For clarity, in fig. Figure 3 shows a line cutting a graph into two parts. Bottom of it is the graph P 6 × P 5 , on which the still unfinished “cycle” is a set of disjoint simple chains. This constructed part of the cycle will be called the “past”. Above the line, one of the possible options for completing an unfinished "cycle" is depicted (this is the "future"). The cycle is closed and does not touch the cut line at its inflection points. And since, going around the cycle in any direction, we will return to the starting point, the cut line will be crossed by the cycle an even number of times.

Figure 3 - Section of the cycle
The intersection of the cycle itself with the cut line can be represented as a regular bracket sequence discharged by zeros. For example, in fig. 3, such a sequence has the form (0000) . In this sequence, a pair of matching opening and closing brackets correspond to the two ends of the same chain going through the “past”, and zeros mean that at these points there is no intersection of the cut line with the cycle. Thus, any incision can be encrypted with the correct bracket sequence discharged with zeros. Since the initial and final sections must be zero (consisting entirely of zeros), we must distinguish between them, denoting one with a line below, and the second with a line above.
In the process of constructing the cycle, we do not need to know either the "past" or the "future", but it is enough to store only information about what section at a given moment in time has turned out, and how the rest can be obtained from this section. Indeed, how to move from the current section to the next? For example, as in fig. 3 it turns out the transition from section (0000) to the next section 00 () 00 ? This will be shown with examples.
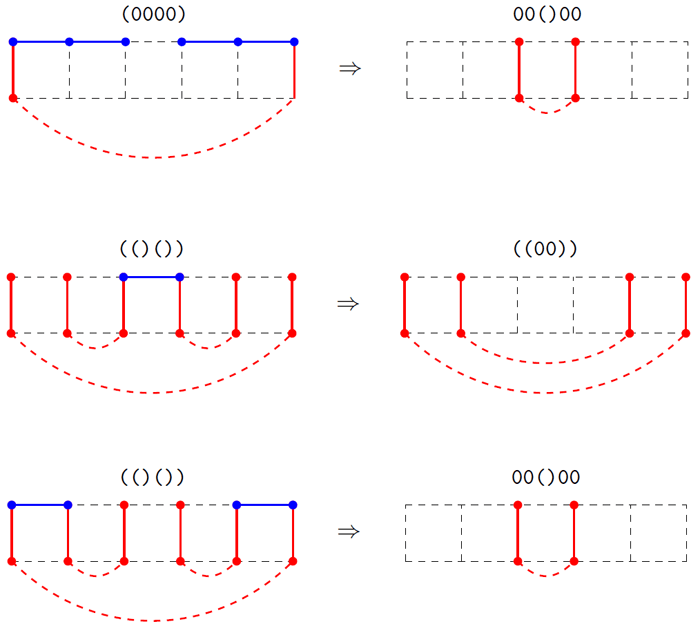
Figure 4 - Examples of the transition from one section to another
In fig. 4 illustrates 3 examples of transitions from one section to another. Arcuate lines show that the ends of their respective vertical arcs are connected through the "past". The first case just shows the transition to Fig. 3 The remaining two cases are slightly more complex, but they clearly demonstrate what new sections can be obtained by adding different combinations of horizontal arcs.
However, not all combinations of horizontal arcs can lead to a new section. Some combinations may turn out to be unacceptable for the three reasons indicated in Figure 5.
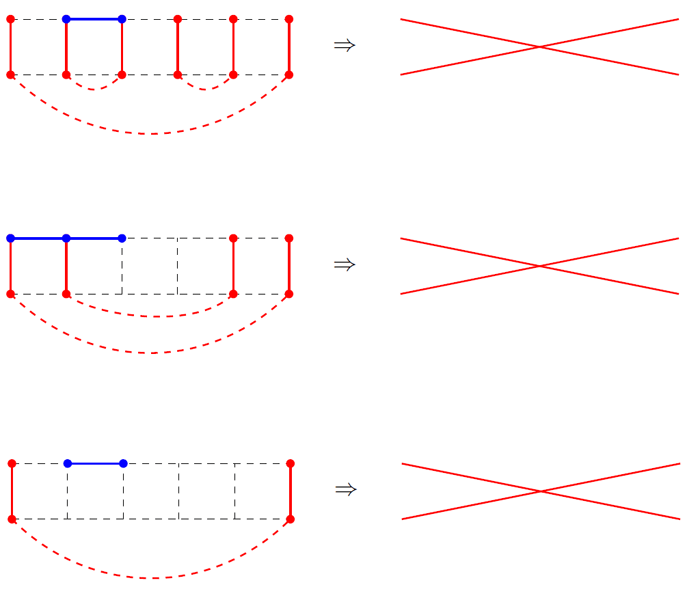
Figure 5 - Examples of invalid transitions. Three possible cases
In the first case, one of the three chains closes ahead of time, so the Hamiltonian cycle cannot turn out. In the second case, three arcs converge at one vertex. Finally, the third case is impossible due to the fact that some vertices are not used (and the Hamiltonian cycle must go through all the vertices).
So, suppose that we have information about all possible sections of our lattice and which sections from which can be obtained by including horizontal arcs. All this information can be represented in the form of a finite state machine, the nodes of which will be cuts, and the arcs will indicate the possibility of transition. In fig. Figure 6 shows an example of such a finite state machine constructed for a 3 × n lattice.
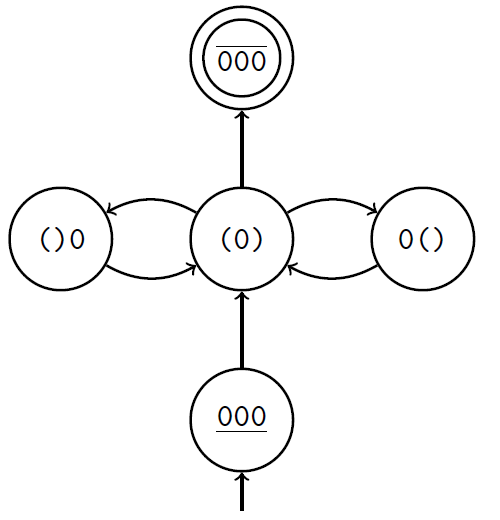
Figure 6 - State machine for a 3 × n lattice
The answer to the question of how many cycles there are on the lattice P 3 × P n will be the number of ways to go from the initial state of the automaton to the final in n steps. How to do it? I know two ways: bad and better. I'll start with the bad.
One way to solve this problem is called the transfer matrix method, which consists in the following. We number all possible cuts from 1 to N in any way, but in such a way that the initial state is number 1 and the final state is number N. Let us construct a matrix T in which the numbers T ij will be equal to the number of ways to get a section with number j from section i . The solution to the problem of the lattice P m × P n is the number (T n ) 1, N .
For example, for the lattice P 3 × P n, we have already constructed an automaton (Fig. 6), so we can write out the transfer matrix.

Figure 7 - Transfer matrix, or adjacency matrix of a finite state machine Fig. 6 and its sixth degree
In fig. 7 shows the transport matrix T for Hamiltonian cycles on the lattice P 3 × P n . The solution to the problem is the number (T n ) 15 . For example, (T 6 ) 15 = 4, such is the number of Hamiltonian cycles on the lattice P 3 × P 6 .
However, in practice, this method of solving the problem is applicable, at most, for m = 12, when the transfer matrix for the Hamiltonian cycles on the lattice has a size of 3774 × 3774 (see Table 1 in the discussion section) and fits in the RAM of a personal computer. Long numbers are stored in the matrix itself, because, for example, the answer for the lattice P 12 × P 20 contains 33 digits, and for the lattice P12 × P 100 the number of digits reaches 174.
The section “Modular Arithmetic” will show how to get rid of long numbers, sacrificing the speed of calculations, but it still will not save from the monstrous growth of the transfer matrix. Therefore, I called this method of solving the problem bad.
This method of solution, as it is not strange, is also called the transfer matrix method, but the matrix does not explicitly appear in it; therefore, it is customary to call this method in the Russian-language literature by the method of dynamic programming [using a finite state machine].
The meaning of the method is to store the number of ways to reach each vertex of the state machine in k steps. At step k = 0, this number is 0 at all vertices except the starting one. By definition, the number of ways to get to the starting vertex at step k = 0 is assumed to be 1. Let P be some methods at vertex i at step k; then, going to step k + 1, we add the number P to the number of methods at all vertices j that can be reached from i. But for this you need to know which vertices you can get from i, that is, again store the matrix! Actually, it’s not necessary: getting to the vertex i, and knowing what section it indicates, we re- build all such sections that can come out of it.
How this is implemented in the program is an individual matter. I will explain my approach. Let there be a queue Q in which sections are stored (in the form of a bracket sequence) and the number of ways to be in them. At the beginning of the algorithm, a section consisting of zeros and a number of methods equal to 1 is stored in the queue. Together with the queue, there is a hash table that also stores sections and the number of ways to end up in them. At the beginning of the algorithm, the table is empty.
At step k, we get the next section i from the queue, and the number of ways P can be in it. We construct the set J of all possible cuts obtained from i. For each j from J, check if it is in the hash table. If not, add j to the table along with the number of methods P. If yes, then from the table we take the number of methods Q that can come to j and write the number P + Q in its place. The exception is the case when j is equal to the zero cut, this means that we are in the final state and must add the number P to the answer, but not add the zero cut to the hash.
At the end of step k, the queue is empty, so we move the data from the hash table to the queue, clear the hash and go to step k + 1.
I use a hash with open addressing and double hashing. The number of collisions is 0.6 per call. That is, in 60% of cases, one step is taken according to the table, and in other cases it gets right away. I find this a good hash for such a task.
First, I will point to the upper limit of complexity, and then I will show what really turns out in practice.
The set of all regular bracket sequences discharged by zeros and of length m are Motskin words of length m over the alphabet { 0 , ( , ) } generated by the context-free grammar
Z → Y | Y ( Z ) Z,
Y → ε | 0 Y,
where ε denotes an empty word. The number of such words can be calculated from combinatorial considerations:

In this formula, k is the number of pairs of brackets. The first expression under the sum sign (fraction and the very first binomial coefficient) is the Catalan number, which shows the number of correct bracket sequences, and the second binomial coefficient is the number of ways to put 2k brackets in m positions (filling the remaining positions with zeros).
Thus, the number of all possible cuts for the Hamiltonian cycles on the lattice, at least, does not exceed the number of Motskin words, and Motskin words grow at a speed of almost 3 m . In fact, there are much fewer such sections, since some may be unacceptable. For example, cuts such as (0) 000 or (() 0) 0 will be unacceptable for a grid of width 6, since they cannot be obtained when constructing the Hamiltonian cycle. In the discussion section, a table will be shown. 1, which indicates the total number of cuts for some m. In reality, it turns out that only a third of Motzkin's words are permissible, and taking into account symmetry, it is enough to store only a fifth of them.
I will explain. Some sections are palindromes and coincide with themselves under symmetrical reflection, but those that are symmetrical to each other can be stored as one section. For example, the cut (()) () and () (()) can be considered the same. With this in mind, it turns out that on average only a fifth of Motzkin's words should be stored in the program.
For each section, we have to sort out 2 m-1ways to put horizontal arcs. And all this together we must do n times.
Total, the algorithm has complexity O (6 m · m -1/2 · n). But in fact, due to the fact that many sections are unacceptable, in practice, the complexity of the algorithm turns out to be O (5 m · n). This happened during my observation of the algorithm.
As for the used memory, the main part of the resources is occupied by the queue and the hash table. Each section for m≤32 can be stored in a 64-bit integer, since 2 bits are required for storing the brackets and the number 0. Plus a long arithmetic that eats up all the resources permanently. But there is one trick that allows you to slow down the calculation, abandoning the long arithmetic.
Let's calculate the answer modulo various prime numbers: 2 31 -1 = 2147483647, 2147483629, 2147483587, ... To do this, you need to run the program as many times as many different modules we choose (although, of course, you can read 2-3 modules at once, as long as it breaks in in memory). According to the Chinese remainder theorem , the answer can be restored up to the product of all the primes used. If the product of all primes is greater than the answer to the problem, then the answer is uniquely restored. How to choose the right number of modules?
For example, let's count the number of cycles on a lattice of size 16 by n for two modules. Let n = 1,2, ..., 16. Then we get the answers
[0, 1, 128, 405688, 24980352, 776813457, 729683652, 1087605227, 2000673777, 456710131, 1550214608, 568568229, 2047094091, 1175631455, 380271385, 1536681549] (mod 2147483647).
[0, 1, 128, 405688, 24980352, 776813727, 729709644, 1107434405, 301217473, 1373982040, 103268356, 218837622, 1185113726, 2085126539, 1315887233, 2008046410] (mod 2147483629).
By the Chinese Remainder Theorem, we have:
[0, 1, 128, 405,688, 24,980,352, 32,989,068,162, 3101696069920, 2365714170297014, 309656520296472068, 2415277789552788286, 3926649012293853406, 726889843182193849, 153366515247378747, 1645735649663585962, 3698490188721496226, 1337259901989820598] (mod · 2147483647 2147483629).
How to check if we had 2 modules? In this problem, it is clear that numbers should grow exponentially, so their logarithms must grow linearly. Let's take logarithms (for example, natural ones):
[-INF, 0, 4.852, 12.91, 17.03, 24.22, 28.76, 35.40, 40.27, 42.33, 42.81, 41.13, 39.57, 41.94, 42.75, 41.74].
The logarithm of the product of our two modules is 42.98. We see that the difference between the numbers monotonously grows by about the same amount, and, starting from n = 9, for some reason they stop growing. Moreover, a limit was reached in this place, beyond which the numbers can no longer be. This means that two modules were not enough. Let's take 4 modules and restore the answer:
[0, 1, 128, 405,688, 24,980,352, 32,989,068,162, 3101696069920, 2365714170297014, 309656520296472068, 168435972906750526954, 27738606105535271640888, 12142048779807437697982030, 2344813362310160031818110686, 888511465584607682074513271223, 191678405883294971709423926242394, 65882516522625836326159786165530572] (mod 2147483647 2147483629 · · · 2147483587 2147483579).
Logarithms are equal:
[-IFN., 0, 4.852, 12.91, 17.03, 24.22, 28.76, 35.40, 40.27, 46.57, 51.68, 57.76, 63.02, 68.96, 74.33, 80.17].
The numbers strictly increase, increasing by about the same amount. The logarithm of the product of 4 selected modules is 85.95, which is noticeably larger than the last number in the sequence. This means that the answer is correct. You can verify this by typing in Google the request "65882516522625836326159786165530572".
With this algorithm, I was able to calculate the number of cycles on a 22 × 100 lattice. The calculations for one module lasted about 30 hours on 32 cores of the cluster. In total, about 50 modules were required. Memory required less than 1 GB per core. In the process of computing, I gathered some information about the quantitative characteristics of the solution. In the table. 1 below is this information.
Table 1 - Comparison of Motskin numbers and the actual number of cuts required for storage in memory.
In the first column, the lattice width m. In the third, the number of Motzkin words of length m. The middle column indicates the actual number of cuts that are valid (symmetry is taken into account and the final state is not calculated).
If you want to see the number of Hamiltonian cycles on a square lattice P 2n × P 2n , then a link to this sequence is in the list of sources.
Thanks for attention.
In the article I will show how to use the dynamic programming method for the profile to solve the problem of counting the number of Hamiltonian cycles on a rectangular lattice of size m by n. On Habré there are several articles devoted to the topic of dynamic programming (for example, this one ), but nowhere is it a question of a more complex application of the method. This approach can also be called the transfer matrix method, as you like.
I warn you that the article contains about 2,000 words (8 A4 pages), but the one who walks will overcome the road.
Summary
- A little bit about difficult tasks
- Definitions and statement of the problem
- Slices and state machine
- Transfer Matrix Method
- Matrix-free solution
- Algorithm complexity
- Modular arithmetic
- Discussions and Results
- List of sources used
1. A little bit about difficult tasks
What is a difficult task? This is a task that does not have an effective solution algorithm. Moreover, this is not necessarily a problem with the exponential complexity of the solution, the complexity can be polynomial, but with a sufficiently large degree of polynomial (for example, the problem of k queens, which I already wrote about here ). More about such problems and their classification can be found in the classic book by M. Gary, D. Johnson, “Computing machines and hard-to-solve problems.”
Such problems are usually solved by brute force, dynamic programming, and combinatorial analysis. Often an acceptable solution is obtained by using these three components at the same time, but this also requires experience in writing fairly optimal code. It’s very good if you have at hand a cluster of at least several thousand cores and at least a couple of hundred gigabytes of RAM. Unfortunately, I’m not joking, many problems can be solved only on such a machine ...
I like to solve difficult problems and from time to time I organize competitions for mathematicians-programmers on this subject. This article is partly dedicated to the Pre-Hamiltonian Cycles contest.”, Which began on October 1 and ends on October 31, 2010. The task proposed in the conditions of the competition is solved by me in the same way (with minor changes), which will be described here.
In the section with the derivation of the complexity of the algorithm, it is assumed that the reader knows the elements of combinatorics (what is the number of combinations, for example), and in the section on the finite state machine, the reader will be forced to recall elements of graph theory (for example, what is the adjacency matrix of a graph, and what gives its construction in power).
2. Definitions and statement of the problem
In this work, we encounter a graph called a rectangular lattice P m × P n . A rectangular lattice is an integer point on the coordinate plane, connected by the principle of closest proximity. The notation P m × P n is due to the fact that an integer rectangle is a direct product of two chains, the first of which has m links (denoted by P m ), and the second by n (denoted by P n ). The number m is the width of the lattice (length from left to right), and n is its length (length from bottom to top).
A Hamiltonian cycle in a graph is a cycle passing through each vertex exactly once. In fig. Figure 1 shows an example of a Hamiltonian cycle on the lattice P 6 × P8 .

Figure 1 - An example of a Hamiltonian cycle on a 6 × 8 lattice
The task is to find the number of Hamiltonian cycles on a lattice P m × P n for given m, n ≥ 2 . For example, the following figure shows all 6 Hamiltonian cycles on a 4 × 4 lattice.

Figure 2 - All 6 Hamiltonian cycles on a 4 × 4 lattice
3. Cuts and state machine
Any cycle in the graph P m × P n can be built sequentially on the “layers” P m × P k (k = 0,1,2, ..., n). For clarity, in fig. Figure 3 shows a line cutting a graph into two parts. Bottom of it is the graph P 6 × P 5 , on which the still unfinished “cycle” is a set of disjoint simple chains. This constructed part of the cycle will be called the “past”. Above the line, one of the possible options for completing an unfinished "cycle" is depicted (this is the "future"). The cycle is closed and does not touch the cut line at its inflection points. And since, going around the cycle in any direction, we will return to the starting point, the cut line will be crossed by the cycle an even number of times.

Figure 3 - Section of the cycle
The intersection of the cycle itself with the cut line can be represented as a regular bracket sequence discharged by zeros. For example, in fig. 3, such a sequence has the form (0000) . In this sequence, a pair of matching opening and closing brackets correspond to the two ends of the same chain going through the “past”, and zeros mean that at these points there is no intersection of the cut line with the cycle. Thus, any incision can be encrypted with the correct bracket sequence discharged with zeros. Since the initial and final sections must be zero (consisting entirely of zeros), we must distinguish between them, denoting one with a line below, and the second with a line above.
In the process of constructing the cycle, we do not need to know either the "past" or the "future", but it is enough to store only information about what section at a given moment in time has turned out, and how the rest can be obtained from this section. Indeed, how to move from the current section to the next? For example, as in fig. 3 it turns out the transition from section (0000) to the next section 00 () 00 ? This will be shown with examples.

Figure 4 - Examples of the transition from one section to another
In fig. 4 illustrates 3 examples of transitions from one section to another. Arcuate lines show that the ends of their respective vertical arcs are connected through the "past". The first case just shows the transition to Fig. 3 The remaining two cases are slightly more complex, but they clearly demonstrate what new sections can be obtained by adding different combinations of horizontal arcs.
However, not all combinations of horizontal arcs can lead to a new section. Some combinations may turn out to be unacceptable for the three reasons indicated in Figure 5.

Figure 5 - Examples of invalid transitions. Three possible cases
In the first case, one of the three chains closes ahead of time, so the Hamiltonian cycle cannot turn out. In the second case, three arcs converge at one vertex. Finally, the third case is impossible due to the fact that some vertices are not used (and the Hamiltonian cycle must go through all the vertices).
So, suppose that we have information about all possible sections of our lattice and which sections from which can be obtained by including horizontal arcs. All this information can be represented in the form of a finite state machine, the nodes of which will be cuts, and the arcs will indicate the possibility of transition. In fig. Figure 6 shows an example of such a finite state machine constructed for a 3 × n lattice.

Figure 6 - State machine for a 3 × n lattice
The answer to the question of how many cycles there are on the lattice P 3 × P n will be the number of ways to go from the initial state of the automaton to the final in n steps. How to do it? I know two ways: bad and better. I'll start with the bad.
4. Transfer matrix method
One way to solve this problem is called the transfer matrix method, which consists in the following. We number all possible cuts from 1 to N in any way, but in such a way that the initial state is number 1 and the final state is number N. Let us construct a matrix T in which the numbers T ij will be equal to the number of ways to get a section with number j from section i . The solution to the problem of the lattice P m × P n is the number (T n ) 1, N .
For example, for the lattice P 3 × P n, we have already constructed an automaton (Fig. 6), so we can write out the transfer matrix.

Figure 7 - Transfer matrix, or adjacency matrix of a finite state machine Fig. 6 and its sixth degree
In fig. 7 shows the transport matrix T for Hamiltonian cycles on the lattice P 3 × P n . The solution to the problem is the number (T n ) 15 . For example, (T 6 ) 15 = 4, such is the number of Hamiltonian cycles on the lattice P 3 × P 6 .
However, in practice, this method of solving the problem is applicable, at most, for m = 12, when the transfer matrix for the Hamiltonian cycles on the lattice has a size of 3774 × 3774 (see Table 1 in the discussion section) and fits in the RAM of a personal computer. Long numbers are stored in the matrix itself, because, for example, the answer for the lattice P 12 × P 20 contains 33 digits, and for the lattice P12 × P 100 the number of digits reaches 174.
The section “Modular Arithmetic” will show how to get rid of long numbers, sacrificing the speed of calculations, but it still will not save from the monstrous growth of the transfer matrix. Therefore, I called this method of solving the problem bad.
5. Solution without using a matrix
This method of solution, as it is not strange, is also called the transfer matrix method, but the matrix does not explicitly appear in it; therefore, it is customary to call this method in the Russian-language literature by the method of dynamic programming [using a finite state machine].
The meaning of the method is to store the number of ways to reach each vertex of the state machine in k steps. At step k = 0, this number is 0 at all vertices except the starting one. By definition, the number of ways to get to the starting vertex at step k = 0 is assumed to be 1. Let P be some methods at vertex i at step k; then, going to step k + 1, we add the number P to the number of methods at all vertices j that can be reached from i. But for this you need to know which vertices you can get from i, that is, again store the matrix! Actually, it’s not necessary: getting to the vertex i, and knowing what section it indicates, we re- build all such sections that can come out of it.
How this is implemented in the program is an individual matter. I will explain my approach. Let there be a queue Q in which sections are stored (in the form of a bracket sequence) and the number of ways to be in them. At the beginning of the algorithm, a section consisting of zeros and a number of methods equal to 1 is stored in the queue. Together with the queue, there is a hash table that also stores sections and the number of ways to end up in them. At the beginning of the algorithm, the table is empty.
At step k, we get the next section i from the queue, and the number of ways P can be in it. We construct the set J of all possible cuts obtained from i. For each j from J, check if it is in the hash table. If not, add j to the table along with the number of methods P. If yes, then from the table we take the number of methods Q that can come to j and write the number P + Q in its place. The exception is the case when j is equal to the zero cut, this means that we are in the final state and must add the number P to the answer, but not add the zero cut to the hash.
At the end of step k, the queue is empty, so we move the data from the hash table to the queue, clear the hash and go to step k + 1.
I use a hash with open addressing and double hashing. The number of collisions is 0.6 per call. That is, in 60% of cases, one step is taken according to the table, and in other cases it gets right away. I find this a good hash for such a task.
6. The complexity of the algorithm
First, I will point to the upper limit of complexity, and then I will show what really turns out in practice.
The set of all regular bracket sequences discharged by zeros and of length m are Motskin words of length m over the alphabet { 0 , ( , ) } generated by the context-free grammar
Z → Y | Y ( Z ) Z,
Y → ε | 0 Y,
where ε denotes an empty word. The number of such words can be calculated from combinatorial considerations:

In this formula, k is the number of pairs of brackets. The first expression under the sum sign (fraction and the very first binomial coefficient) is the Catalan number, which shows the number of correct bracket sequences, and the second binomial coefficient is the number of ways to put 2k brackets in m positions (filling the remaining positions with zeros).
Thus, the number of all possible cuts for the Hamiltonian cycles on the lattice, at least, does not exceed the number of Motskin words, and Motskin words grow at a speed of almost 3 m . In fact, there are much fewer such sections, since some may be unacceptable. For example, cuts such as (0) 000 or (() 0) 0 will be unacceptable for a grid of width 6, since they cannot be obtained when constructing the Hamiltonian cycle. In the discussion section, a table will be shown. 1, which indicates the total number of cuts for some m. In reality, it turns out that only a third of Motzkin's words are permissible, and taking into account symmetry, it is enough to store only a fifth of them.
I will explain. Some sections are palindromes and coincide with themselves under symmetrical reflection, but those that are symmetrical to each other can be stored as one section. For example, the cut (()) () and () (()) can be considered the same. With this in mind, it turns out that on average only a fifth of Motzkin's words should be stored in the program.
For each section, we have to sort out 2 m-1ways to put horizontal arcs. And all this together we must do n times.
Total, the algorithm has complexity O (6 m · m -1/2 · n). But in fact, due to the fact that many sections are unacceptable, in practice, the complexity of the algorithm turns out to be O (5 m · n). This happened during my observation of the algorithm.
As for the used memory, the main part of the resources is occupied by the queue and the hash table. Each section for m≤32 can be stored in a 64-bit integer, since 2 bits are required for storing the brackets and the number 0. Plus a long arithmetic that eats up all the resources permanently. But there is one trick that allows you to slow down the calculation, abandoning the long arithmetic.
7. Modular arithmetic
Let's calculate the answer modulo various prime numbers: 2 31 -1 = 2147483647, 2147483629, 2147483587, ... To do this, you need to run the program as many times as many different modules we choose (although, of course, you can read 2-3 modules at once, as long as it breaks in in memory). According to the Chinese remainder theorem , the answer can be restored up to the product of all the primes used. If the product of all primes is greater than the answer to the problem, then the answer is uniquely restored. How to choose the right number of modules?
For example, let's count the number of cycles on a lattice of size 16 by n for two modules. Let n = 1,2, ..., 16. Then we get the answers
[0, 1, 128, 405688, 24980352, 776813457, 729683652, 1087605227, 2000673777, 456710131, 1550214608, 568568229, 2047094091, 1175631455, 380271385, 1536681549] (mod 2147483647).
[0, 1, 128, 405688, 24980352, 776813727, 729709644, 1107434405, 301217473, 1373982040, 103268356, 218837622, 1185113726, 2085126539, 1315887233, 2008046410] (mod 2147483629).
By the Chinese Remainder Theorem, we have:
[0, 1, 128, 405,688, 24,980,352, 32,989,068,162, 3101696069920, 2365714170297014, 309656520296472068, 2415277789552788286, 3926649012293853406, 726889843182193849, 153366515247378747, 1645735649663585962, 3698490188721496226, 1337259901989820598] (mod · 2147483647 2147483629).
How to check if we had 2 modules? In this problem, it is clear that numbers should grow exponentially, so their logarithms must grow linearly. Let's take logarithms (for example, natural ones):
[-INF, 0, 4.852, 12.91, 17.03, 24.22, 28.76, 35.40, 40.27, 42.33, 42.81, 41.13, 39.57, 41.94, 42.75, 41.74].
The logarithm of the product of our two modules is 42.98. We see that the difference between the numbers monotonously grows by about the same amount, and, starting from n = 9, for some reason they stop growing. Moreover, a limit was reached in this place, beyond which the numbers can no longer be. This means that two modules were not enough. Let's take 4 modules and restore the answer:
[0, 1, 128, 405,688, 24,980,352, 32,989,068,162, 3101696069920, 2365714170297014, 309656520296472068, 168435972906750526954, 27738606105535271640888, 12142048779807437697982030, 2344813362310160031818110686, 888511465584607682074513271223, 191678405883294971709423926242394, 65882516522625836326159786165530572] (mod 2147483647 2147483629 · · · 2147483587 2147483579).
Logarithms are equal:
[-IFN., 0, 4.852, 12.91, 17.03, 24.22, 28.76, 35.40, 40.27, 46.57, 51.68, 57.76, 63.02, 68.96, 74.33, 80.17].
The numbers strictly increase, increasing by about the same amount. The logarithm of the product of 4 selected modules is 85.95, which is noticeably larger than the last number in the sequence. This means that the answer is correct. You can verify this by typing in Google the request "65882516522625836326159786165530572".
8. Discussions and results
With this algorithm, I was able to calculate the number of cycles on a 22 × 100 lattice. The calculations for one module lasted about 30 hours on 32 cores of the cluster. In total, about 50 modules were required. Memory required less than 1 GB per core. In the process of computing, I gathered some information about the quantitative characteristics of the solution. In the table. 1 below is this information.
| m | The actual number of cuts | Motzkin's Word Count |
|---|---|---|
| 3 | 3 | 4 |
| 4 | 6 | 9 |
| 5 | 12 | 21 |
| 6 | 23 | 51 |
| 7 | 62 | 127 |
| 8 | 109 | 323 |
| 9 | 365 | 835 |
| 10 | 607 | 2188 |
| eleven | 2355 | 5798 |
| 12 | 3774 | 15511 |
| thirteen | 16020 | 41835 |
| 14 | 25188 | 113634 |
| fifteen | 113198 | 310572 |
| 16 | 176061 | 853467 |
| 17 | 821923 | 2356779 |
| 18 | 1270562 | 6536382 |
| 19 | 6097041 | 18199284 |
| 10 | 9387784 | 50852019 |
| 21 | 46013564 | 142547559 |
| 22 | 70652188 | 400763223 |
Table 1 - Comparison of Motskin numbers and the actual number of cuts required for storage in memory.
In the first column, the lattice width m. In the third, the number of Motzkin words of length m. The middle column indicates the actual number of cuts that are valid (symmetry is taken into account and the final state is not calculated).
If you want to see the number of Hamiltonian cycles on a square lattice P 2n × P 2n , then a link to this sequence is in the list of sources.
9. List of sources used
- M. Gary, D. Johnson. Computers and difficult tasks.
- A003763 - Number of Hamiltonian cycles on 2n X 2n square grid of points.
- Chinese remainder theorem .
- Catalan numbers , derivation of the formula and asymptotics.
Thanks for attention.
