A model of a natural series of numbers and its elements. Rhombuses

In this work, the basic G 2 ± model is retained , but a different organization of its cells is accepted (another figure). On top of the primary lattice with 1 × 1 cells , a larger grid is represented - a grid of rhombuses, and also a grid of centers of rhombuses is considered (SCR). The last grid is not depicted so as not to overload the lines with the pattern with rhombuses. We will not repeat the definitions and concepts that were described in detail in previous works , but give links pointing to these works.
Constructive description of the model
Through the cells G 2 ± - models contained in even long D i and short K i diagonals with numbers ending with zeros within the G 2 - - submodel, lines are drawn that form a large network of rhombuses in the plane. The rhombic regions for cells collectively cover the entire plane without gaps. Each rhombus contains 41 cells, of which only 16 are of interest, and when probing a rhombus, only 4 cells with fixed flexion are used.
The characteristics of rhombs will include:
- the number of cells in the rhombus;
- the value of the number in the central cell;
- the numbers of its horizontal ( N i ) and vertical ( V i );
- identifying cells for numbers with inflections 1, 3, 7, 9;
- the coordinates of these cells in the coordinate system of the rhombus with the origin in the central cell of the rhombus.
A grid of rhombus centers is also constructed through the cells of the rhombus centers, the nodes of which are located in the cells at the intersection of long and short diagonals with numbers that are multiples of the number 5.
From the figure with rhombuses it is clear what kind of grid we are talking about. To illustrate the features of rhombuses, images of a pair of rhombuses in each half-plane are given. These rhombuses are marked with identifying numbers of cells in the lower half and another pair of such rhombuses in the upper half-planes. Marking of rhombuses in a half-plane below the diagonal D 0differs from the marking of rhombuses in the half-plane above it, but within the same half-plane, the marking of all rhombuses is identical for both the lower and upper half-planes. The essence of marking is the localization of cells with numbers that have equal inflections (marked by filling the cells with the same color), setting their coordinates x 1 , x 0 . The designated rhombuses will be called fundamental; other rhombuses with zooming in may be formed from them.
The centers of the rhombuses of the lower half-plane are cells with numbers ending in two digits either 25 with the horizontal number with flexion 5 and with the vertical number with flexion 0, or 75 with the horizontal number with flexion 0 and with the vertical number with flexion 5. In the upper half-plane Г 2 +- submodels, all numbers in the central cells of all rhombuses end with two digits 25. Further, we restrict our consideration to the half-plane Г 2 - . Figure 1- The visual representation of the model with rhombuses Definition 1. Fundamental rhombus - structure T 2 ± - model bounded by two short and two long diagonals of this plane with the numbers that are multiples of 10. The main element characterizing diamond, is a cell ( X 1C , X 0c ) of its center. The center contains the numerical value of N, a multiple of 5. Definition 2.
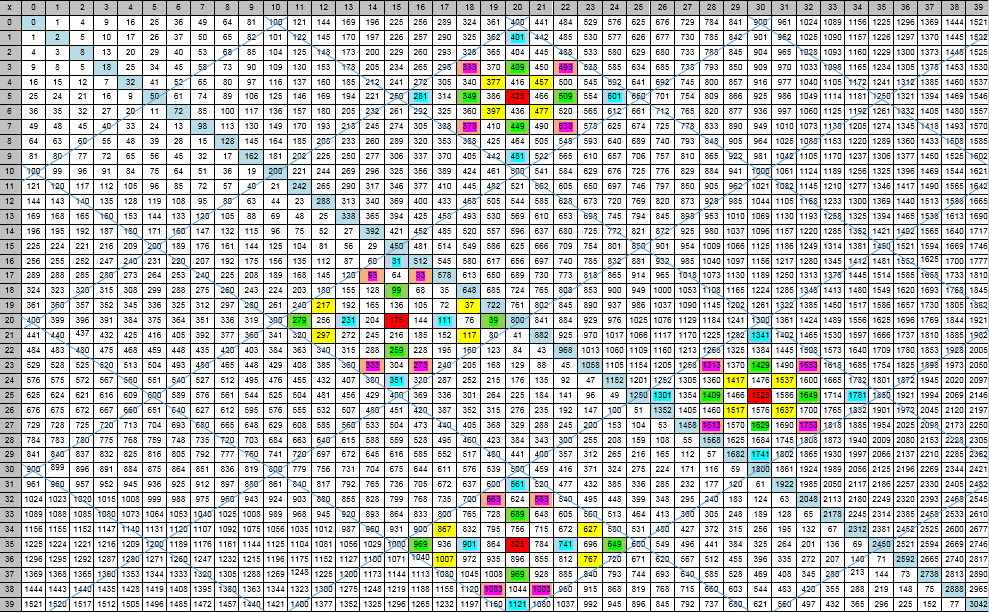
The set of centers of fundamental rhombuses is the nodes (cells) of the network of centers of rhombuses (SCR) of intersecting short and long diagonals, with numbers that are multiples of 5. The rhombuses themselves completely cover the plane Г 2 ± - models (parquet principle).
All rhombuses are arranged in the same way, and the numbers in their cells with fixed endings are placed in fixed positions (cells). This allows us to solve the problem of localizing the number Nin a certain rhombus, it is easy to factorize this number. Ten horizontals whose cells form a rhombus and neighboring rhombuses (with coordinates different from it) will be called a strip of rhombuses. Horizontal bands are considered: West-East (ЗВ); vertical: North-South (NW), along short diagonals: Northeast (NE) and along long diagonals: North-West (NW). The offset from one rhombus to another can be supplemented by an indication (up and down) along the indicated bands, in addition to indicating the strip.
Since it follows from Definition 2 that the set of cells of all rhombuses is all the cells of the G 2 ± model, then in one of the cells (x 1p , x 0p )belonging to some rhombus, it is necessary to find a given composite odd positive integer (ELF) N (x 1p , x 0p ) = N (x 1 , x 0 ) . At the same time, we believe that it is possible to indicate such a rhombus (by determining the coordinates of its central cell) (x 1c , x 0c ) than to probe all cells, even confining itself to probing only odd diagonals.
Indication of such a rhombus and the desired cell within it is a solution to the localization problem for a given number N (x 1 , x 0 ). This problem and its solution precede the receipt of the decision of the WFCH. The meaning and ultimate goal of the localization problem is to indicate in a certain rhombus for a given ELF N (x 1 , x 0 ) the values of the coordinates of the cell (x 1p , x 0p ) in the G 2 ± model, in which there is a number coinciding with N (x 1 , x 0 ) .
In this article, we use the mechanism for establishing the belonging of a given number N to a specific rhombus and a cell in it. This mechanism is far from the best, but in the proposed examples it copes with the task. Readers are invited to either offer their original, or improve this mechanism.
Our mechanism is based on the remarkable regularity of the G 2 ± model discovered by the author : the presence in the horizontal lines with numbers that are multiples of five (and some others), cells with squares of the elements of the Pythagorean triples (PFT) < g, k 1 , k 2 > = <hypotenuse , leg 1 , leg 2 >. The CFT will be discussed in another work.
To simplify the conclusions and calculations, we need three coordinate systems: planar, which has already been introduced , network with other numbers of diagonals for the SCR (Fig. 2) and rhombic (Table 1), in which the beginning is associated with the cell of the center of the rhombus.

Figure 2. Numbering (double) of short diagonals and
distribution of rhombus centers on short diagonals
Table 1. Determining the coordinates of a search point within a fixed rhombus

In the SCR system are indicated: the number of the short diagonal n p , q is the serial number of the center on it, and also the network-wide C center number, own numbering of short diagonals starting from n p = 1(in the planar system this is the 5th short diagonal), then the number n p = 2 (this is the number increased by 10, i.e. the 15th planar K i ) and then with the step 10 all the others. The position of all the cells of the rhombus centers in each K i of the SCR is also numbered from c = 1 to c = 2n p of the double network number of the short diagonal.
Example 1 . Suppose you want to find the network-wide number C of the center of one of the rhombuses and the number N in this cell for a given short diagonal passing through the centers of rhombuses, its network number n p = 5 , and the serial number of the center c = 3one of the rhombs on it. Quite simply, the network coordinates of the center cell of this rhombus are represented in the form (n p , q) = (5, 3) .
- Find the plane x 1 coordinate of the cell at the beginning of the given diagonal (nd):
x 1 = x nd = 10n p - 5 = 50 - 5 = 45.
For our case, we got x 1 = x nd = 45 . - Now we can immediately proceed to the search for the plane coordinates of the cell ( x 1c , x sc ) of the desired center: x 1 = x nd - 5 (c - 1) = 45 - 5 (3 - 1) = 35, x 0 = 0 + 5 ( μ - 1) = 2 ∙ 5 = 10.
- Find the network number of the center of the rhombus ( C ).
Comment. It is known that for the number x the formula 2C x + 1 2 = x (x + 1) is the doubled number of combinations of x + 1 in two.
The number of centers preceding the short diagonal n p = 5 is 2n p (n p - 1) . Then the serial number C of the network center is given by the formula
C = n p (n p -1) + c = 2C n p 2 + 3 = 5 ∙ 4 + 3 = 23 . - Find the value of the number N (x 1c , x sc ) in the cell of the center of the rhombus N = x 1 2 - x 0 2 - the sign in the formula is taken depending on the position of the center relative to the main diagonal.
N = 35 2 - 10 2 = 1125 - for our case.
Thus, having only the network number n p of the short diagonal passing through the cells of the centers and the current center number of the rhombus c on this diagonal, we can obtain all other information about the center of the rhombus.
All odd positive integers of interest N belong to diamond cells. The concept of flexion, the last digit of a number, allows to localize their position within rhombs. For factorization, those numbers N that end with the numbers 1, 3, 7, 9 are of interest .
Even numbers are not considered as N , since they have a prime divisor 2. Numbers ending with five have a prime divisor 5, which is also unacceptable for N. It is advisable to localize a specific N by inflection within the rhombus relative to the center of the rhombus, in the context of the fact that the center is the most important characteristic of the rhombus. Based on the fact that all rhombuses have the same structure, there is a clear relationship between the number N specified for factorization and the numbers in rhombus cells with certain inflections and in the cell of the rhombus center. Data on such relationship numbers are given in table. 1.
However, sorting out all rhombuses on a plane to find the desired rhombus is unacceptable either in time or in computational cost. Thus, the problem arose of localizing the regions Г 2 - - submodels (half-planes) including rhombuses that would contain the initial number Nsubject to factorization.
Pythagorean triples . To solve the formulated problem, we use
Pythagorean triples — triples of numbers that satisfy the Pythagorean theorem: Namely, Pythagorean triples that satisfy the rule of the so-called Egyptian triangle, that is, a triangle with sides that are multiples of 3, 4, 5.
In each horizontal x 1 containing centers of rhombuses, there is one or more such Pythagorean triples.
The first rhombus in the localization problem is indicated approximately and in case of a “miss”, the following rhombuses should be selected. For this, it is necessary to determine the direction of movement along the SCR, so as to gradually approach the final goal. For example, if the smaller of the 4 in the current rhombus of numbers is less than the given N, then the North-East and East rhombuses from it contain even less than 4 numbers, that is, such rhombs should not be probed. Moving to the Western rhombus leads to such an increase in values in all 4 of its cells that even a smaller number of the Western rhombus turns out to be larger than the larger number of the previous rhombus and, therefore, more than N. Hence the solution: move up from the rhombus to the rhombus in the north-west direction.
If a rhombus containing a cell with a number equal to N (x 1p , x 0p ) =N is found and the cell coordinates (x 1p , x 0p ) are determined, then the solution of the FBCH is determined by the basic relation Г 2 ± - of the model
N = x 2 1 - x 2 0 = (x 1 - x 0 ) (x 1 + x 0 ) = p ∙ q
Another subproblem is the selection and implementation of a sequence of bypassing the cells of the rhombus selected for probing. Here, the anticlockwise traversal order is adopted, starting from the upper left cell containing the number with the required inflection. In a situation of coincidence of values in the diamond cell N (x 1p , x 0p) and a given number N (x 1 , x 0 ), the difference between them turns out to be zero.
ZFBCH solution algorithm using fundamental rhombuses and PFT
- Extract root of the number N . Round down.
- We check if √N is divisible by 3. If divisible, then assign this value to the first leg k1, otherwise, to fulfill the divisibility property by 3, subtract 1 or 2 from the result, and enter it into memory as k1. The result of dividing the fully selected value by three M = √N / 3 - remember the scaling PFT coefficient.
- Get the value of the second leg k 2 , according to Egyptian triangle rule, k 2 = M 4 ∙ .
- We find the value of the hypotenuse g = 5 ∙ M , and the value x 1 = g should be divided by the number five. As you can see, the value of the hypotenuse is always equal to the horizontal number with PFT.
- Find the coordinate x 1 = g .
- After that, we determine the inflection (last digit) of the number N , φ = N (mod10) .
- We find the center of the rhombus closest to k1 and then examine adjacent rhombuses in one of the bands of rhombuses (there are 4 directions) to find a solution.
- Depending on what kind of inflection we get in paragraph 6, we use the desired column (mask) from those presented in table. 1 to determine the coordinates of the search point ( x 1p , x 0p ) and find the value of the number in this cell N p . In each rhombus, only 4 cells are checked from the 41st cell.
- After establishing that the number N belongs to a particular rhombus and a cell in it, based on the same table. 1 we get the plane coordinates N: (x 1p , x 0p ) .
- Using the properties of the selected mathematical model
N = x 2 1 - x 2 0 = (x 1 - x 0 ) (x 1 + x 0 ) = p ∙ q
we obtain the multiplicative representation of N from the additive. - Thus, at the output of the algorithm, we have: N = p ∙ q . Depending on the value of flexion f according to the formulas in table. 1, the coordinates of the point (x 1p , x 0p ) are determined and the difference ∆ = N (x 1p , x 0p ) - N (x 1 , x 0 ) is calculated . If ∆ ≠ 0 , then go to another cell, if all the cells of the rhombus are checked, then to another rhombus.
If Δ = 0 , then x 1 = x 1p , x 0 = x 0p and p = (x 1 - x0 ) , q = N / p = (x 1 + x 0 ) .
Example 2. Given: N = 1037 , a number with a capacity of 4. It is required to factorize it. We act according to the given algorithm.
- Extract the root of N : √N = 32,202 . We round down: √N = 32 .
- We check if 32 is divisible by 3. Since 32 is not divisible by 3, we subtract 2. So, we assume that the first leg is k 1 = 3 ∙ 10 = 30 , here M = 10 = 30/3 is the PFT scaling factor .
- We get the value for the second leg k 2 = 4 ∙ 10 = 40 .
- We find the hypotenuse value g = (k 2 1 + k 2 2 ) 0.5 , provided that it is divided by 5, (30 2 +40 2 ) 0.5 = 50.
- Thus, x1 = k1 = 50 and the PFT transforms to the form g = 50 , k 1 = 30, k 2 = 40 .
- We find the inflection of the number N : φ (1037) = 1037 (mod10) = 7 .
- We find the center of the rhombus closest to N = 1037 .
It will have the coordinates of the central cell of the rhombus: x 1 = 50, x 0 = 35 . The first coordinate is the line number containing the CFT. The square of the smaller leg is 900, it is contained in the vertical with number 40. The cell with the number 957 ending with the seven closest to 900 lies in the previous horizontal with the number 49 and in the vertical with the number 38. This is the smallest number of 4 in the rhombus and with inflection 7. Here we use the data of table 1. The nearest center of the rhombus should be three cells to the left, that is, it belongs to the vertical 38 - 3 = 35, this is the second coordinate of the center of the rhombus. The value of the number in the cell of the center of the rhombus is N (50, 35) = 1275
This is a rhombus having square legsk 1 and k 2 at their borders. Within this rhombus, min is a number ending in seven 957 in a cell ( x 1 = 49, x 0 = 38 ), and another number in this vertical ending in 7th 1157 , large numbers 1377 and 1577 lie to the left of the central cell, coinciding with the number N = 1037 no, therefore, it is necessary to rise to the rhombus to the left and higher with a value in the central cell of 1125 and with the coordinates of the central cell ( x 1 = 50 - 5 = 45, x 0 = 35 - 5 = 30) We check the four numbers for inflection 7. These are 847, 1027, 1207 and 1387 and there are no matches with N = 1037 in this rhombus ), we will rise even higher in the same direction along the strip of northwestern rhombs. The center cell of the new rhombus has a value of 975 and coordinates ( x 1 = 45 -5 = 40, x 0 = 35 - 5 = 25 ). Check the numbers at the four diamond 7. This inflexion 737, 897, 1197 and finally obtain 1037 in the cell ( x 1p = 39, x 0P = 22 ) received a full match with a given N .
In detail, these actions are represented by the following calculations: In accordance with Table 1, we calculate the coordinates of the cells and the number values in them. After that, we find the differences between the calculated and given values of N. In the first rhombus, all 4 cells are calculated.
∆ = N (x 1c -1, x 0c -3) - N (x 1 , x 0 ) = N (49.32) - 1037 = 1377 - 1037 = 340 ≠ 0,
∆ = N (x 1c +1, x 0ts -3) - N (x 1 , x 0 ) = N (51.32) - 1037 = 1577 - 1037 = 540 ≠ 0,
∆ = N (x 1ts +1, x 0ts +3) - N (x 1 , x 0 )= N (51.38) - 1037 = 1157 - 1037 = 120 ≠ 0,
∆ = N (x 1ts -1, x 0ts +3) - N (x 1 , x 0 ) = N (49.38) - 1037 = 957 - 1037 = - 80 ≠ 0.
In this rhombus there is no coincidence of the number N with the numbers in the cells.
We go to the next rhombus with the center in the cell (x 1c -5, x 0c -5) = (45, 30) and the value in it N (x 1c -5, x 0c -5) = N (45, 30) = 1125 .
∆ = N (x 1c -1, x 0c -3) - N (x 1 , x 0 ) = N (44.27) - 1037 = 1207 - 1037 = 170 ≠ 0,
∆ = N (x1c +1, x 0c -3) - N (x 1 , x 0 ) = N (46.27) - 1037 = 1387 - 1037 = 350 ≠ 0,
∆ = N (x 1c +1, x 0c +3) - N (x 1 , x 0 ) = N (46.33) - 1037 = 1027 - 1037 = - 10 ≠ 0,
Δ = N (x 1ts -1, x 0ts +3) - N (x 1 , x 0 ) = N (44.33) - 1037 = 847 - 1037 = - 190 ≠ 0.
In this rhombus, there is no coincidence of the number N with the numbers in the cells either.
Go to the next rhombus with the center in the cell (x 1c -5, x 0c -5) = (40, 25) and the value in itN (x 1c - 5, x 0c - 5) = N (40, 25) = 975
∆ = N (x 1c -1, x 0c -3) - N (x 1 , x 0 ) = N (39.22 ) - 1037 = 1037 - 1037 = 0.
We got a zero difference of values. There is a complete coincidence. From this it follows that the given number N (x 1 , x 0 ) = 1037 is contained in the cell with coordinates (x 1p , x 0p ) = (39, 22). Finally, the solution of the HFBC is determined by the main relation Г 2 ± - of the model
N = x 2 1 - x 2 0= (x 1 - x 0 ) (x 1 + x 0 ) = (39 - 22) (39 + 22) = p ∙ q = 17 ∙ 61 . - You can act differently. Starting with the rhombus indicated in paragraph 6, using table. 1, we find out whether the number N belongs to a particular rhombus, moving between the centers of the rhombs first horizontally, towards the main diagonal, then moving down to the next strip of rhombs and repeating everything again.
- After establishing that the number N belongs to a certain rhombus (in our case, the rhombus will have coordinates ( x 1 = 40, x 0 = 25 )) based on the same table. 1 we get the coordinates N : x 1p = 39 , x 2p = 22 (9 rhombs viewed).
- Using the properties of the chosen mathematical model of the number
N = x 2 1 - x 2 0 = (x 1 - x 0 ) (x 1 + x 0 ) = p ∙ q
we obtain the multiplicative representation of N from the additive:
N = (39 - 22) (39 + 22) = 17 ∙ 61 = 1037 .
Thus, at the output we have N = p · q = 17 · 61 = 1037 , i.e., the solution to the problem was obtained successfully.
We also get the result of a software solution to the problem in Example 3.
Example 3 . Given: N = 3808572773, a number with a resolution of 10.
- We extract the root from N: √N = 61713 , 64 = 61713 .
- We check if 61713 is divisible by 3. Since 61713 is divisible by 3,
6 + 1 + 7 + 1 + 3 = 18 is divisible by 3, the first leg k 1 is equal to k 1 = 61713 . - We obtain a second leg k 2 = 4k 1 /3 => 4k 2 /3 = 82284 .
- We find the hypotenuse g = √k 12 + k 22 , provided that it is divided by
5 · g = √617132 + 822842 = 102855 . - Thus, x 1 = k 1 = 61713 , and the Pythagorean triple transforms respectively to the form k 1 = 61713, k 2 = 82284, g = 102855 .
- We find the inflection of the number N: f (3808572773) = 3808572773 (mod10) = 3 .
- We find the nearest center of the rhombus. It will have the coordinates x 1 = 61715; x 9 = 0 .
- Starting with the rhombus indicated in paragraph 7, using the data in table. 1, we find out whether the number N belongs to a particular rhombus, moving between the centers of the rhombs first horizontally, towards the main diagonal, then shifting to the next strip of rhombuses and repeating everything again.
- After establishing that the number N belongs to a certain rhombus (in our case, the center of the rhombus will have coordinates x 1 = 62015 , x 0 = 6085 ) we get N :
x 1p = 62013; x 0p = 6086 ; (60 diamonds examined). - Using the properties of the selected mathematical model
N = x 2 1 - x 2 0 = (x 1 - x 0 ) (x 1 + x 0 ) = p · q we obtain the multiplicative representation of N from the additive:
N = (62013 - 6086) · (62013 + 62086) = 55927.68099 = 3808572773 ; - Thus, at the output we have N = p · q = 55927 · 68099 = 3808572773 , i.e., the solution to the problem was obtained successfully.
