Found evidence that all changes are a mixture of order and chance

All descriptions of the changes are a unique mixture of chance and determinism, according to the radical proof of Pinsker's “weak hypothesis”

Imagine a garden where all the flowers of the world grow - delicate orchids, towering sunflowers, wax flowers of the Carnegie cactus and stinky inflorescences of the titanic amorphophallus . Now imagine that all this plant diversity has come down to just two options, and that by crossing them, you can produce all the others.

This is the nature of one of the most radical evidence obtained in recent years. It was made by Tim Austin , a mathematician from the University of California at Los Angeles. But instead of flowers, Austin’s work is associated with one of the most studied objects in mathematics: a mathematical description of changes.

These descriptions, known as dynamic systemsapply to everything from planetary movements to stock market fluctuations. Wherever a dynamic system arises, mathematicians want to understand its fundamentals. And one of the basic facts is that any arbitrarily complex dynamic system can be divided into random and deterministic elements.

This question is the subject of the Pinsker's “weak hypothesis,” which was first formulated in the 1970s. The proof of the hypothesis presented by Austin provides an elegantly intuitive method of thinking about all sorts of obscure phenomena. He showed that, in essence, each of these dynamic systems is a mixture of chance and determinism.

Fate and chance

A dynamic system starts with some input data, for example, with the position of the pendulum, applies certain rules, for example, Newton’s laws of motion, and produces a certain result, for example, the position of the pendulum in one second. What is important, dynamic systems allow you to repeat this process: you can take a new position of the pendulum, apply the same rules, and get its position in another second.

Dynamic systems are also purely mathematical. You can select the starting number, apply the rule "multiply the number by two" and get a new one. This system also allows you to enter the total number back into the rule handler and get even more numbers.

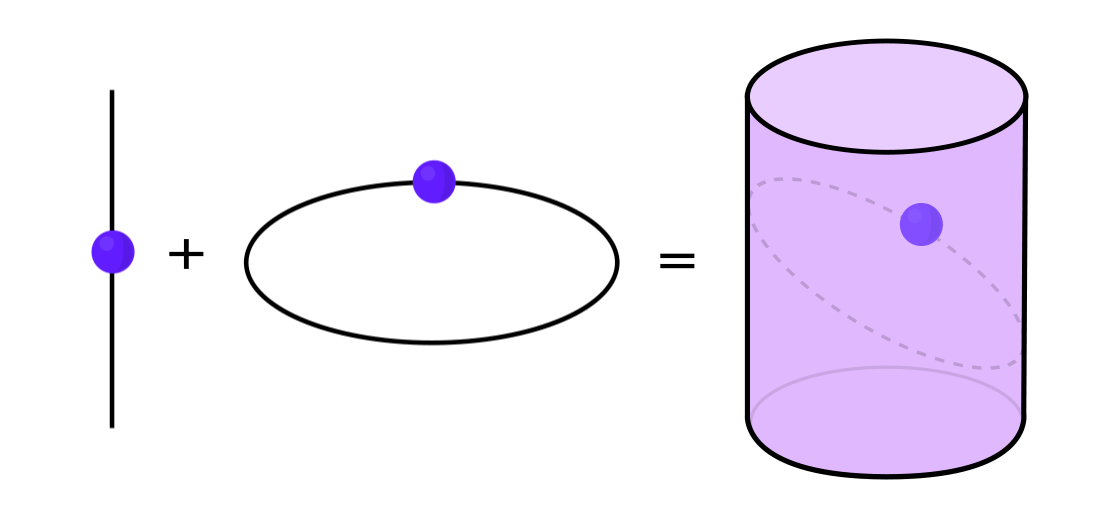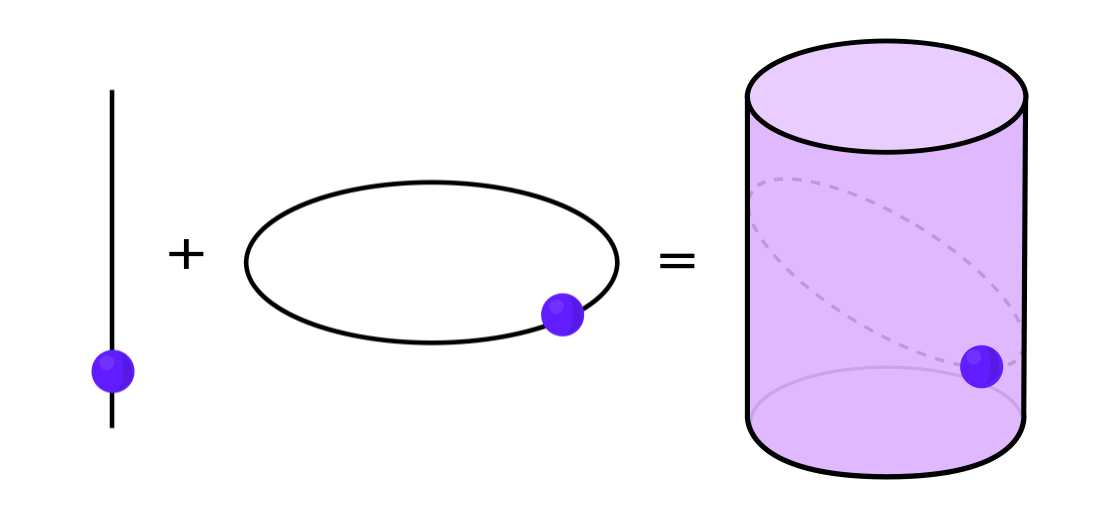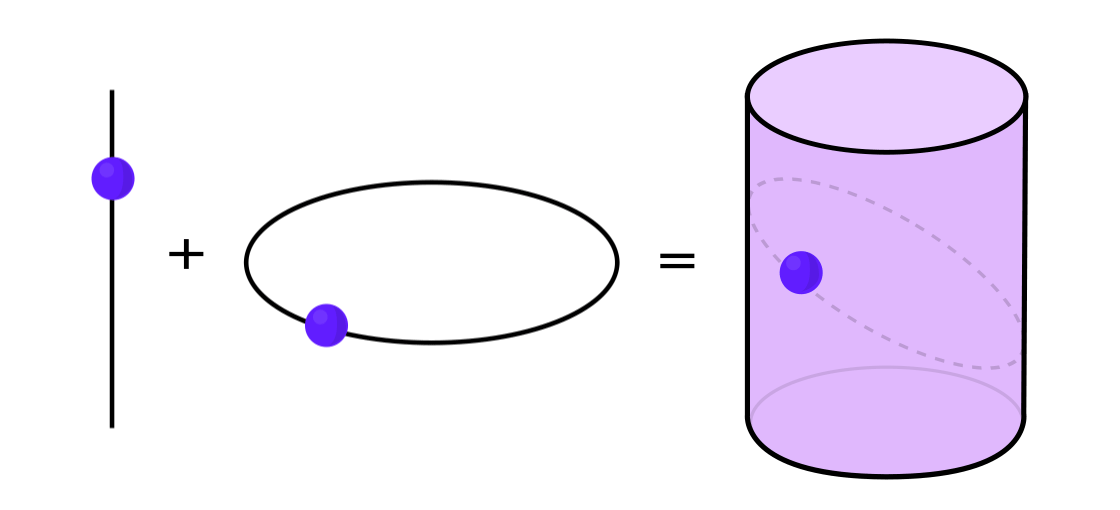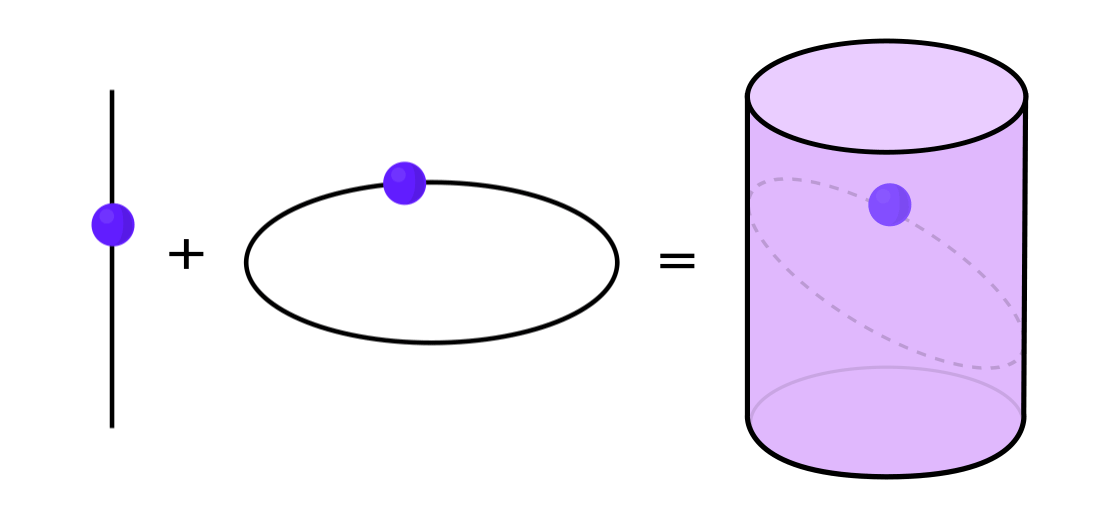
Certain types of dynamical systems can be expressed as a combination of two simpler dynamical systems. These two systems work independently of each other, but they can be combined to form a more complex one. For example, imagine a dynamic system moving a point along the surface of a cylinder. You enter the position of the point, apply the rules, and get another point.

This system can be disassembled into two simple ones. The first is a dynamic system moving a point around a circle. The second is a system that moves a point up and down vertically. By combining two systems — circular motion and straight motion — we obtain a more complex point motion along the cylinder.



“Instead of studying the entire dynamical system as a whole, you need to break it into parts, small parts that make sense to study,” saidKatherine Lindsay , a mathematician at Boston College.

There are two natural candidates for the role of these building blocks. The former are fully deterministic dynamical systems, such as our pendulum example. If you know the position of the pendulum at some point in time, you can predict it at any time in the future.


Jean-Paul Tuveno in 1975, two years before the formulation of the Pinsker's weak hypothesis. The

second type of dynamical systems is completely random. For example, imagine a dynamic system with this rule: toss a coin. If there is an eagle, take a step to the left; if tails, right. The final path will be completely random, that is, even if you know everything about the previous path, this information will not help you predict the next step.

Some dynamic systems are completely random, others are completely deterministic, and most are somewhere in between - they are a hybrid of both. For example, imagine a slightly modified version of our random walk. We walk along a path along the edge of which flowers are planted, and their colors are also random. The rule remains the same: if an eagle falls, go left; if tails, right. What will be the sequence of flowers colors?

First you say random. After all, the colors themselves were chosen randomly, and your movement is also random. However, after you have passed a single flower, the likelihood that you will pass it in the future increases, simply because you are not far from it. The sequence of flower colors will not be completely random.

“If you stand next to the red, it increases the chances that in two steps you will meet the red again, because it may happen that you step to the left, then to the right, and return to the same place,” Austin said.

Such a “random walk through a random landscape” produces output — a sequence of colors — partly random and partly not. In 1960, mathematician Mark Pinsker suggested that a certain large class of dynamical systems has the following property: they are a mixture of a random dynamical system with a deterministic one.

Pinsker's conjecture is applicable to the class of dynamical systems that have an important common property. The points in them do not depart far from each other and do not shrink during the development of the system. More precisely, if you draw a loop around a set of points in your space (the space may be something like a cylinder surface), start the development of a dynamic system for a long period of time, and then draw a loop around the resulting set of points, then the area that the points in end, coincides with the area they occupied at the beginning. Such systems are called “measure preserving."

“If Pinsker's original hypothesis were correct, it would be an amazing description of the world,” said Assaf Naor , a mathematician at Princeton University. But Pinsker was wrong. In 1973Donald Ornstein disproved his hypothesis. “The wording was too ambitious,” said Brina Kra , a mathematician at Northwestern University.

In mathematics, it often happens that after the general hypothesis is refuted, mathematicians try to formulate a more modest version of it. In 1977, the mathematician Jean-Paul Tuveno proposed the weak Pinsker hypothesis. He softened the original formulation, suggesting that the dynamic systems that Pinsker had in mind were the result of combining a purely random system with a system that was almost completely deterministic.

Refinement “almost” distinguishes Tuveno’s hypothesis from Pinsker's hypothesis. He meant that a simple deterministic system should have some trace of chance. This trace may be disappearing small, but should be there. And while he is, Tuveno said, Pinsker's idea will work.

“It was close to the original hypothesis, and Tuveno showed that if so, then the hypothesis will have a huge number of excellent applications,” said Naor.

In the following decades, mathematicians did not achieve much success in proving Pinsker's weak hypothesis. The lack of progress made Tuveno think that even his weakened wording would turn out to be wrong. “At one point, I thought that everything would be the opposite, that it would not be universal,” he said.

And then Tim Austin appeared.

Step solution

To prove Pinsker's weak hypothesis, it was necessary to find an exact way to sift through a dynamic system — one that would allow it to separate its random and almost deterministic parts. Previous work has established that it will be most difficult to isolate elements with a little randomness.

“Small random factors are much harder to catch, and the central part of the evidence is finding a way to detect a small random structure,” Tuveno said.


Tim Austin, a mathematician at the University of California, Los Angeles

Austin managed to deal with small random elements of a dynamic system by changing perspectives. Dynamic systems operate on a continuous space, such as a point moving along the surface of a cylinder, or a pendulum swinging in space. In these spaces, points move along continuous arcs in accordance with the rules of a dynamical system. Also, these systems work on an infinite number of steps - they can act forever.

But in his proof, Austin abandoned continuous smooth space and forgot about the eternal work of dynamical systems. Instead, he began to analyze what would happen if they were allowed to work discrete times, such as a million steps. Thus he applied the method invented by Tuveno.

“Tuveno’s main contribution was that he realized that if you perform the correct mathematical steps with long finite lines, you can prove the properties of a dynamical system,” Austin said. “My main contribution was that I proved what was needed for the long end lines.”

Austin imagined a dynamic system issuing a sequence of ones and zeros. If the dynamic system is tossing a coin, then it’s easy to imagine: the tails will be 1 and the heads will be 0. But any dynamic system can be used to generate a binary sequence by simply dividing the space in which it works into two (not necessarily equal) parts.



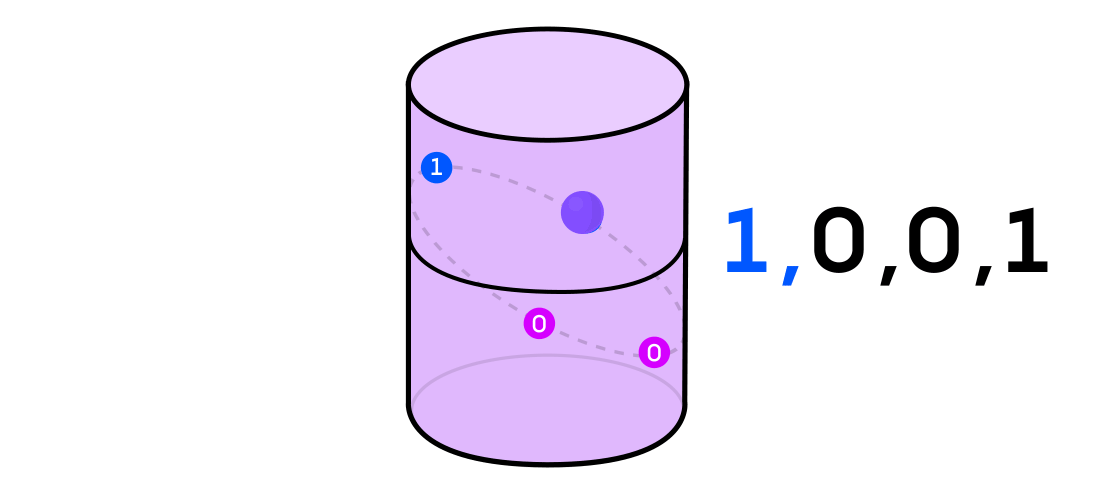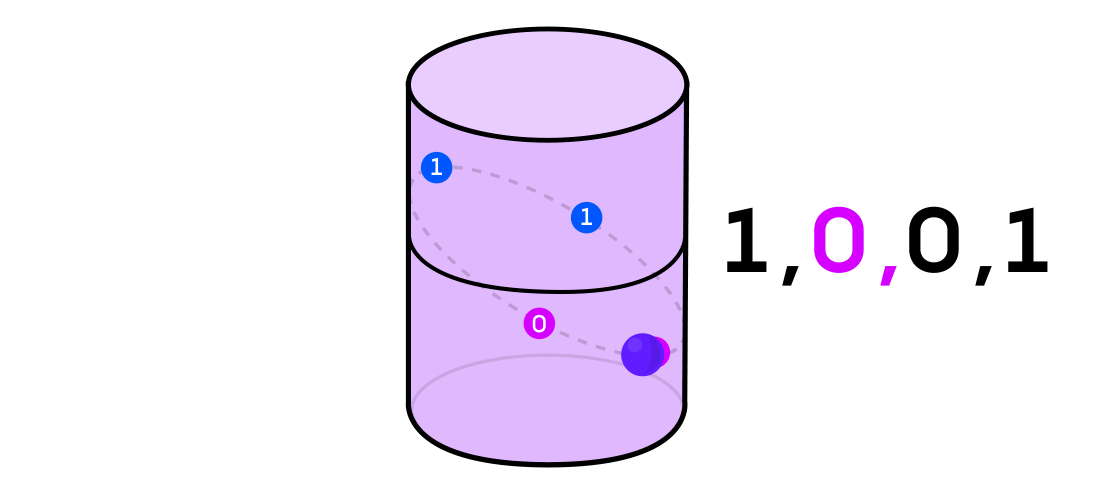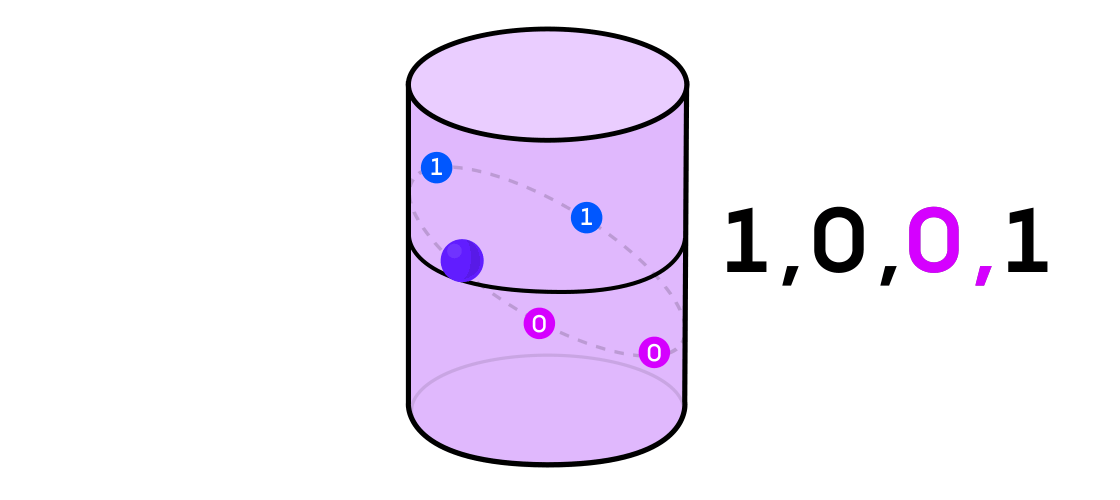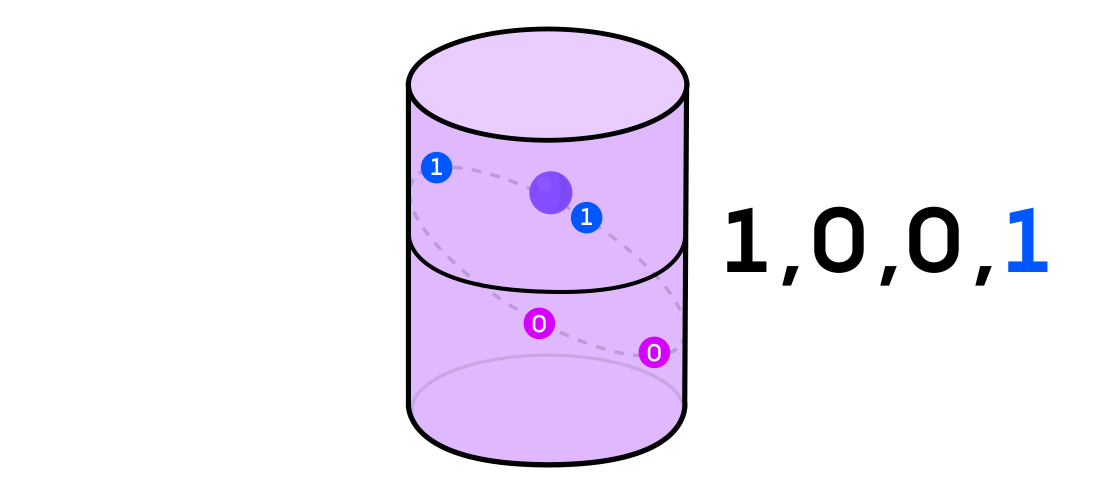
Returning to the example of a dynamic system on a cylinder, if the point is on one part of the cylinder, you denote the output value of system 1, and if on the other, then 0.

Austin analyzed these binary sequences using an information theory tool called “ Hamming cubes ”. Imagine a cube of vertices connected by edges. Binary numbers are assigned to each vertex — say, 001 or 101. Each time, when switching from one vertex to another, one of the three digits changes.

Hamming cubes can be much more complicated than ours, they can have as many more edges and vertices in more dimensions than three - but they all have the property, due to which the distance between any two vertices - or the number of edges that you need to go to go from one vertex to another is equal to the number of places in which the information lines corresponding to these vertices are distinguished. Therefore, 000 is located at the distance of one edge from 001, two edges from 011 and three from 111.



To isolate the random and deterministic elements that make up a complex dynamic system, Austin thought about how often a dynamic system can produce a given sequence of zeros and ones represented on a Hamming cube. He proved that these sequences are distributed in a cube in a certain way. They accumulate in a small number of cube subregions - and this cluster reflects the determinism of the system - however, they are randomly distributed among the sequences within these clusters, which reflects the randomness of the system.

Such a roundabout was necessary to solve a problem that did not give in to direct attacks.

“What surprised me was not so much the truth or falsity of Pinsker's weak hypothesis, but how it turned out to prove, because this task seemed so insidious,” said Lewis Bowen, a mathematician at the University of Texas at Austin. “Before the evidence appeared, we, by and large, had no idea whether this could be done at all.”

Austin's result gives the basic structure to a wide range of dynamical systems. To mathematicians, who often revolve among objects that seem interconnected, it’s not clear how the proof gives their exact geography. Now they have a guide for these dynamic systems, although it is still unknown what kind of discoveries this will lead to.

“Mathematicians are always interested in the building blocks that make up anything,” Lindsay said. “Austin’s proof is an excellent result, which is likely to have many applications in pure mathematics, but I can’t say what they will be.”