How quantum computing can affect software development
- Transfer
Hello!
For about the last six months, the publishing house has been actively working on the topic of quantum computing and their practical applicability. For a long time it was not possible to find a worthy article for translation on this interesting topic, until such an article appeared on the Oracle blog. The publication will serve as an excellent introduction to the software, hardware, and purely natural science problems of this new paradigm, so reading is a must.

Over the past months and years, interest in quantum computing has grown significantly. New materials are constantly appearing from research institutes, companies or government organizations, telling about breakthrough achievements in this area. At the same time, articles with a weaker technical basis discuss the potential consequences of quantum computing, and forecasts range from hacking most modern encryption techniques to promises to cure all diseases and complete work on creating a full-fledged AI. However, not all of these expectations are equally realistic.
If you are a practicing sober programmer, then you might be wondering where the line between facts and fiction is in these calculations, and how quantum computing will affect software development in the future.
Naturally, many years remain before the creation of working hardware for quantum computing. However, the general principles of this paradigm are already understood today, there are abstractions that allow developers to create applications in which the possibilities of quantum computing are realized using simulators.
Traditional software development using classic computers involves translating a high-level programming language (for example, Java) into operations performed on a large number of (hardware) transistors.
In Figure 1, this process is schematized in its simplest form: Java source code is compiled into platform-independent byte code, which, in turn, is translated into platform-specific machine code. Machine code uses a number of simple operations (gates) performed in memory. The main hardware component used for this purpose is the well-known transistor.

Fig. 1. Translation of a high-level programming language into operations performed on transistors .
The increase in productivity achieved in recent years has been achieved mainly due to the improvement of hardware technologies. The sizes of a single transistor have drastically decreased, and the more transistors you can put on each square millimeter, the more memory and processing power the computer will have.
Quantum computing is a disruptive technology, because here the simplest computing units are not classical transistors, but qubits, which we will talk about below.
The point is not only in the differences of these primary elements, but also in a different device of valves. Thus, the stack with fig. 1 in quantum computing is not applicable.
In short - "not really." Scientists are gradually agreeing that quantum computers will be especially good for solving specific problems, while other problems will be more rationally solved using traditional computers. Sounds familiar, right? A similar situation is observed when comparing the GPU and CPU. While transistors are also used in the GPU, they differ in principle from the CPU. However, many applications written in a high-level language use the capabilities of both the CPU and the GPU under the hood. GPUs are very good for vector processing, and in many applications and libraries the work of the CPU and GPU is differentiated.
For example, this is exactly the situation when using JavaFX or Deeplearning4j. If you are writing a user interface application using JavaFX, then you only work with Java code (maybe also FXML to declare a user interface). When the JavaFX scene needs to be displayed on the screen, internal JavaFX implementations use shaders and textures for this, directly contacting the low-level GPU drivers, as shown in Figure 2. Therefore, you don’t have to worry about which part of the code is better adapted to work with the CPU and which with GPU.

Fig. 2. JavaFX delegates the work of the GPU and CPU.
As shown in fig. 2, JavaFX implementation code delegates the work by passing it to the GPU and CPU. Although these operations are hidden from the developer (not provided through the API), certain knowledge of the GPU is often useful when you need to develop more powerful JavaFX applications.
When using Deeplearning4j, a similar situation develops. Deeplearning4j has a number of implementations for performing the required vector and matrix operations, and some of them use GPUs. However, it doesn’t matter to you as an end developer which capacities your code will use - CPU or GPU.
It seems that quantum computers will do an excellent job of solving problems that, as a rule, increase exponentially as the volume of the problem grows and, therefore, can hardly be solved or almost unsolvable using classical computers. In particular, experts talk about a hybrid embodiment: a typical end-to-end application contains classic code that runs on the CPU, but it may also contain quantum code.
Today, hardware for quantum computers is still extremely experimental. While large corporations and, presumably, some states are engaged in the development of prototypes, such technology is not widely available. But, when it appears, its shape may be different:
Although there remains enormous uncertainty about the practical background of such decisions, we are increasingly agreeing on how a quantum code should look. At the lowest level should be the following bricks: qubits and quantum gates . Based on them, you can create quantum simulators that implement the expected behavior.
Therefore, a quantum simulator is an ideal tool for such a development.
The results they give should be almost the same as they would be obtained on real equipment of a quantum computer - but the simulator works much slower, since quantum effects that accelerate quantum equipment have to be simulated using traditional software.
It is often important to compare classical calculations with quantum ones. In classical computing, we have bits and gates.
A bit contains a single bit of information, and its value may be 0 or 1.
The gate acts on one or more bits and can operate on them. For example, the NOT valve, shown in Figure 3, reverses the value of a bit. If the input is 0, then the output of the NOT gate will be 1 and vice versa.

Fig. 3. NOT Gate
In quantum computing, we have equivalent bits and gates. The quantum equivalent of a bit is qubit. The value of a qubit can be equal to 0 or 1, like a classic bit, however, it can also be in the so-called superposition. This is a complex concept, according to which a qubit can simultaneously be in both states: 0 and 1.
When a qubit is in superposition, its value is a linear combination of states 0 and 1. This can be written as shown in Fig. 4:

Fig. 4. Equality where the qubit is in superposition.
Note: qubits are often written in bracket notation , where the variable name is placed between the characters "|" and ">".
The expression in Fig. 4 reports that qubit x is in a superposition of states | 0> and | 1>. This does not mean that it is in the state | 0> OR in the state | 1>; this means that his current state is not known to us.
In fact, it is in both states at the same time, and in this form it can be manipulated. However, when we measure the qubit, it will be in one state, either | 0> or | 1>. In the above expression, there is another restriction: a ^ 2 + b ^ 2 = 1.
The values a and b are probabilistic: there is a probability a ^ 2 that, when we measure the qubit | x>, it will contain the value | 0>, and probability b ^ 2 that the measured qubit will contain the value | 1>.
There is an important limiting factor breaking off the joys of quantum computing: after a qubit is measured, all information about the potential superposition in which it was located is lost. The qubit value can be 0 or 1.
In calculations, a qubit in superposition can correspond to 0 and 1 at the same time (with different probabilities). If we have two qubits, then they can be used to represent four states (00, 01, 10, and 11), again, with different probabilities. Here we come to the essence of the power of quantum computers. Having eight classic bits, you can represent exactly one number in the range from 0 to 255. The values of each of the eight bits will be 0 or 1. Having eight qubits, you can simultaneously represent all numbers from 0 to 255.
Often the result of the algorithm is simple (yes or no), but to arrive at it, a lot of parallel computing is required. Holding qubits in superposition during calculations, you can immediately take into account any many different options. Without fulfilling decisions for each individual combination, a quantum computer can calculate all the options in one step.
Then, in many quantum algorithms, the next important stage begins: to connect the result of the algorithm with a measurement that gives a meaningful result. Often, interference is taken into account: interesting results are structurally superimposed on each other, while uninteresting ones cancel each other out (destructive interference).
Just as classical gates manipulate bits, quantum gates manipulate qubits. Some quantum gates resemble classical ones; for example, the Pauli-X gate transfers the qubit from the state a | 0> + b | 1> to the state b | 0 | + a | 1>, which is similar to the principle of the classic NOT gate. Indeed, when a = 1 and b = 0, the qubit was initially in the state | 0>. After the action of the Pauli-X valve, this qubit will go into the state | 1>, as shown in Fig. 5.
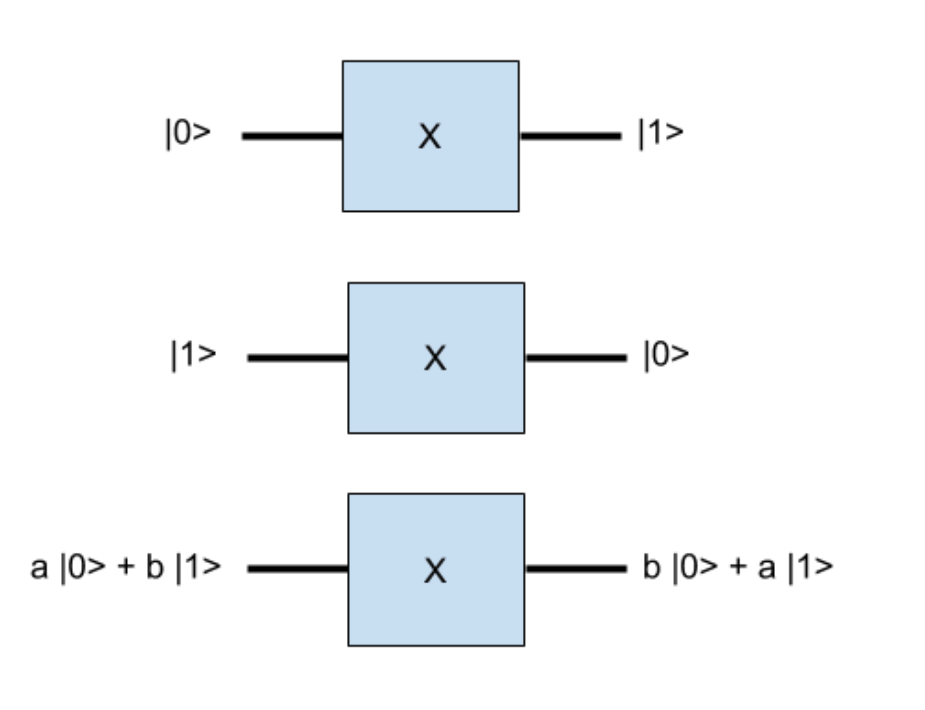
Fig. 5. The result of using the Pauli-X valve.
In this context, the Hadamard valve is very interesting. It puts the qubit in the state | 0>: 1 / sqrt (2) * (| 0> + | 1>) into a superposition, as shown in Fig. 6.

Fig. 6. The result of applying the Hadamard valve.
After we apply the Hadamard valve to a qubit and measure the qubit, there is a 50% probability that the qubit value will be 0 and 50% that the qubit value will be 1. Until the qubit is measured, it remains in a superposition state .
If you are really interested in the answer to this question, you will have to study quantum physics in detail. But, fortunately, the entire theoretical basis of these phenomena is not required to be understood. While the phenomenon of superposition may seem incomprehensible, it is important to emphasize that it is these properties that are characteristic of elementary particles in nature. Therefore, quantum computing is much closer to the basics of physical reality than it seems at first glance.
Not. In this case, you will be late. It is theoretically possible to first develop the hardware, and then proceed to the study of the software level and see what can be achieved with it. However, all the concepts are already more or less clear, and it is already possible to write quantum simulators in popular languages, including Java, C #, Python and others.
Then these simulators can be used to work on quantum algorithms. Although, these algorithms will not give such a performance increase that is achievable with their help when working on real quantum equipment, they should functionally be completely complete.
Thus, if you are currently developing a quantum algorithm, then you have time to improve it, and you can start it when quantum equipment appears in access.
Quantum algorithms require a different intellectual approach than classical ones. Prominent scientists started developing quantum algorithms back in the last century, and now more and more articles are published describing such algorithms, including those for integer multiplication, list search, path optimization work, and much more.
There are other reasons why it might be worth doing quantum computing today. Refactoring a software system in a modern large company is not one of those things that can be done overnight. However, one of the areas in which quantum computing will make a real revolution is encryption; after all, it is all based on the theory that on a classical computer it is practically impossible to decompose a large integer into prime factors.
Although it may take many years before quantum computers become large enough to easily solve the problem of integer factorization, developers know that it takes many years to change systems and introduce new, safer technologies into them.
You can download and master Strange , the open source quantum computer simulator in Java. Strange allows you to simulate a quantum algorithm by creating a series of qubits and applying several quantum gates to them.
As a simple example, let's create two qubits, q [0] and q [1], so that initially both of them are in state 0. Then we apply two simple gates to each of the qubits, so that graphically this operation corresponds to fig. 7.
The first qubit will first go to the Pauli-X valve, and then to the Hadamard valve. The Pauli-X valve will transfer it from the state | 0> to | 1>, and the Hadamard valve will translate it into a superposition with equal probabilities | 0> and | 1>. Therefore, if we complete the entire sequence 1000 times and measure the first qubit 1000 times at the end of this cycle, then on average we can expect that it will have a value of 0 in 500 cases and a value of 1 in 500 cases. The
second qubit is even simpler. We start with the Identity gate, which does not change the behavior of the qubit, and then pass it to the Pauli-X gate, changing its value from 0 to 1.
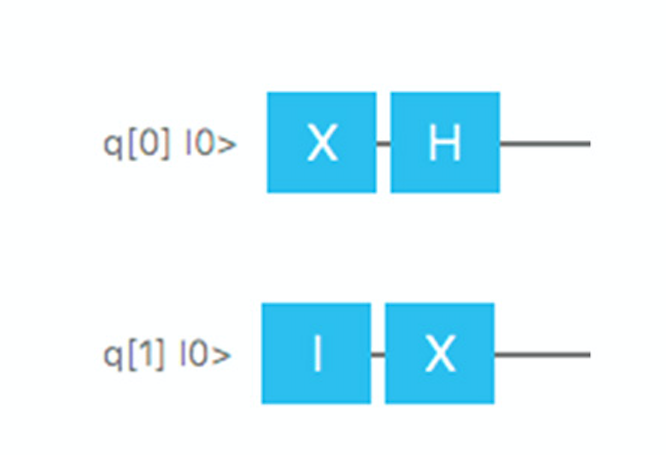
Fig. 7. An example of a quantum algorithm that can be simulated using Strange.
To make sure our reasoning is correct, you can create a simple quantum program using Strange.
In this application, a quantum program with two qubits is created:
As part of this program, we go through two stages. In the first step, apply the Pauli-X valve to q [0]. We do not apply the valve to q [1], and thus imply that it will work with the Identity valve. Add this step to the program:
Then we pass to the second stage, where we apply the Hadamard valve to q [0] and the Pauli-X valve to q [1]; add this step to the program:
So, our program is ready. Now let's do it. A quantum simulator is built into Strange, however, Strange can also use a cloud service to run programs in some kind of cloud, for example, in Oracle Cloud .
In the following example, we use a simple built-in simulator, run the program and get the resulting qubits:
Before we measure the qubits (and lose all the information), we display the probabilities. Now measure the qubits and look at the values:
By launching this application, we get the following conclusion: Note: for the first qubit, the value 0 can also be measured, as we expected. If you run this program many times, then the value of the first qubit on average will be 0 in half the cases and 1 in half the cases.
Of course not. Here we did not touch upon a number of important concepts, in particular, we did not discuss the intricacies that ensure the interaction between two qubits, even if physically they are very far from each other. We did not talk about the most famous quantum algorithms, among them the Shore algorithm, which allows decomposing integers into prime factors. We also ignored a number of mathematical and physical facts, in particular, did not take into account that in the superposition | x> = a | 0> + b | 1>, both numbers a and b can be complex.
However, the main purpose of this article was to give you the impression of quantum computing and to understand how they fit into the future of software development.
For about the last six months, the publishing house has been actively working on the topic of quantum computing and their practical applicability. For a long time it was not possible to find a worthy article for translation on this interesting topic, until such an article appeared on the Oracle blog. The publication will serve as an excellent introduction to the software, hardware, and purely natural science problems of this new paradigm, so reading is a must.

Over the past months and years, interest in quantum computing has grown significantly. New materials are constantly appearing from research institutes, companies or government organizations, telling about breakthrough achievements in this area. At the same time, articles with a weaker technical basis discuss the potential consequences of quantum computing, and forecasts range from hacking most modern encryption techniques to promises to cure all diseases and complete work on creating a full-fledged AI. However, not all of these expectations are equally realistic.
If you are a practicing sober programmer, then you might be wondering where the line between facts and fiction is in these calculations, and how quantum computing will affect software development in the future.
Naturally, many years remain before the creation of working hardware for quantum computing. However, the general principles of this paradigm are already understood today, there are abstractions that allow developers to create applications in which the possibilities of quantum computing are realized using simulators.
Are quantum computing reduced to another CPU gain?
Traditional software development using classic computers involves translating a high-level programming language (for example, Java) into operations performed on a large number of (hardware) transistors.
In Figure 1, this process is schematized in its simplest form: Java source code is compiled into platform-independent byte code, which, in turn, is translated into platform-specific machine code. Machine code uses a number of simple operations (gates) performed in memory. The main hardware component used for this purpose is the well-known transistor.

Fig. 1. Translation of a high-level programming language into operations performed on transistors .
The increase in productivity achieved in recent years has been achieved mainly due to the improvement of hardware technologies. The sizes of a single transistor have drastically decreased, and the more transistors you can put on each square millimeter, the more memory and processing power the computer will have.
Quantum computing is a disruptive technology, because here the simplest computing units are not classical transistors, but qubits, which we will talk about below.
The point is not only in the differences of these primary elements, but also in a different device of valves. Thus, the stack with fig. 1 in quantum computing is not applicable.
Will quantum computing break the entire stack above down to the Java level?
In short - "not really." Scientists are gradually agreeing that quantum computers will be especially good for solving specific problems, while other problems will be more rationally solved using traditional computers. Sounds familiar, right? A similar situation is observed when comparing the GPU and CPU. While transistors are also used in the GPU, they differ in principle from the CPU. However, many applications written in a high-level language use the capabilities of both the CPU and the GPU under the hood. GPUs are very good for vector processing, and in many applications and libraries the work of the CPU and GPU is differentiated.
For example, this is exactly the situation when using JavaFX or Deeplearning4j. If you are writing a user interface application using JavaFX, then you only work with Java code (maybe also FXML to declare a user interface). When the JavaFX scene needs to be displayed on the screen, internal JavaFX implementations use shaders and textures for this, directly contacting the low-level GPU drivers, as shown in Figure 2. Therefore, you don’t have to worry about which part of the code is better adapted to work with the CPU and which with GPU.

Fig. 2. JavaFX delegates the work of the GPU and CPU.
As shown in fig. 2, JavaFX implementation code delegates the work by passing it to the GPU and CPU. Although these operations are hidden from the developer (not provided through the API), certain knowledge of the GPU is often useful when you need to develop more powerful JavaFX applications.
When using Deeplearning4j, a similar situation develops. Deeplearning4j has a number of implementations for performing the required vector and matrix operations, and some of them use GPUs. However, it doesn’t matter to you as an end developer which capacities your code will use - CPU or GPU.
It seems that quantum computers will do an excellent job of solving problems that, as a rule, increase exponentially as the volume of the problem grows and, therefore, can hardly be solved or almost unsolvable using classical computers. In particular, experts talk about a hybrid embodiment: a typical end-to-end application contains classic code that runs on the CPU, but it may also contain quantum code.
How can a system execute quantum code?
Today, hardware for quantum computers is still extremely experimental. While large corporations and, presumably, some states are engaged in the development of prototypes, such technology is not widely available. But, when it appears, its shape may be different:
- A quantum coprocessor can be integrated with the CPU in the system.
- Quantum problems can be delegated to quantum cloud systems.
Although there remains enormous uncertainty about the practical background of such decisions, we are increasingly agreeing on how a quantum code should look. At the lowest level should be the following bricks: qubits and quantum gates . Based on them, you can create quantum simulators that implement the expected behavior.
Therefore, a quantum simulator is an ideal tool for such a development.
The results they give should be almost the same as they would be obtained on real equipment of a quantum computer - but the simulator works much slower, since quantum effects that accelerate quantum equipment have to be simulated using traditional software.
What are the basic building blocks of quantum computing?
It is often important to compare classical calculations with quantum ones. In classical computing, we have bits and gates.
A bit contains a single bit of information, and its value may be 0 or 1.
The gate acts on one or more bits and can operate on them. For example, the NOT valve, shown in Figure 3, reverses the value of a bit. If the input is 0, then the output of the NOT gate will be 1 and vice versa.

Fig. 3. NOT Gate
In quantum computing, we have equivalent bits and gates. The quantum equivalent of a bit is qubit. The value of a qubit can be equal to 0 or 1, like a classic bit, however, it can also be in the so-called superposition. This is a complex concept, according to which a qubit can simultaneously be in both states: 0 and 1.
When a qubit is in superposition, its value is a linear combination of states 0 and 1. This can be written as shown in Fig. 4:

Fig. 4. Equality where the qubit is in superposition.
Note: qubits are often written in bracket notation , where the variable name is placed between the characters "|" and ">".
The expression in Fig. 4 reports that qubit x is in a superposition of states | 0> and | 1>. This does not mean that it is in the state | 0> OR in the state | 1>; this means that his current state is not known to us.
In fact, it is in both states at the same time, and in this form it can be manipulated. However, when we measure the qubit, it will be in one state, either | 0> or | 1>. In the above expression, there is another restriction: a ^ 2 + b ^ 2 = 1.
The values a and b are probabilistic: there is a probability a ^ 2 that, when we measure the qubit | x>, it will contain the value | 0>, and probability b ^ 2 that the measured qubit will contain the value | 1>.
There is an important limiting factor breaking off the joys of quantum computing: after a qubit is measured, all information about the potential superposition in which it was located is lost. The qubit value can be 0 or 1.
In calculations, a qubit in superposition can correspond to 0 and 1 at the same time (with different probabilities). If we have two qubits, then they can be used to represent four states (00, 01, 10, and 11), again, with different probabilities. Here we come to the essence of the power of quantum computers. Having eight classic bits, you can represent exactly one number in the range from 0 to 255. The values of each of the eight bits will be 0 or 1. Having eight qubits, you can simultaneously represent all numbers from 0 to 255.
What is the use of superposition if you can measure only one state?
Often the result of the algorithm is simple (yes or no), but to arrive at it, a lot of parallel computing is required. Holding qubits in superposition during calculations, you can immediately take into account any many different options. Without fulfilling decisions for each individual combination, a quantum computer can calculate all the options in one step.
Then, in many quantum algorithms, the next important stage begins: to connect the result of the algorithm with a measurement that gives a meaningful result. Often, interference is taken into account: interesting results are structurally superimposed on each other, while uninteresting ones cancel each other out (destructive interference).
How can one “transform” a qubit into a state of superposition?
Just as classical gates manipulate bits, quantum gates manipulate qubits. Some quantum gates resemble classical ones; for example, the Pauli-X gate transfers the qubit from the state a | 0> + b | 1> to the state b | 0 | + a | 1>, which is similar to the principle of the classic NOT gate. Indeed, when a = 1 and b = 0, the qubit was initially in the state | 0>. After the action of the Pauli-X valve, this qubit will go into the state | 1>, as shown in Fig. 5.

Fig. 5. The result of using the Pauli-X valve.
In this context, the Hadamard valve is very interesting. It puts the qubit in the state | 0>: 1 / sqrt (2) * (| 0> + | 1>) into a superposition, as shown in Fig. 6.

Fig. 6. The result of applying the Hadamard valve.
After we apply the Hadamard valve to a qubit and measure the qubit, there is a 50% probability that the qubit value will be 0 and 50% that the qubit value will be 1. Until the qubit is measured, it remains in a superposition state .
How is all this possible?
If you are really interested in the answer to this question, you will have to study quantum physics in detail. But, fortunately, the entire theoretical basis of these phenomena is not required to be understood. While the phenomenon of superposition may seem incomprehensible, it is important to emphasize that it is these properties that are characteristic of elementary particles in nature. Therefore, quantum computing is much closer to the basics of physical reality than it seems at first glance.
Should I wait a few years, and then take a closer look at quantum computing?
Not. In this case, you will be late. It is theoretically possible to first develop the hardware, and then proceed to the study of the software level and see what can be achieved with it. However, all the concepts are already more or less clear, and it is already possible to write quantum simulators in popular languages, including Java, C #, Python and others.
Then these simulators can be used to work on quantum algorithms. Although, these algorithms will not give such a performance increase that is achievable with their help when working on real quantum equipment, they should functionally be completely complete.
Thus, if you are currently developing a quantum algorithm, then you have time to improve it, and you can start it when quantum equipment appears in access.
Quantum algorithms require a different intellectual approach than classical ones. Prominent scientists started developing quantum algorithms back in the last century, and now more and more articles are published describing such algorithms, including those for integer multiplication, list search, path optimization work, and much more.
There are other reasons why it might be worth doing quantum computing today. Refactoring a software system in a modern large company is not one of those things that can be done overnight. However, one of the areas in which quantum computing will make a real revolution is encryption; after all, it is all based on the theory that on a classical computer it is practically impossible to decompose a large integer into prime factors.
Although it may take many years before quantum computers become large enough to easily solve the problem of integer factorization, developers know that it takes many years to change systems and introduce new, safer technologies into them.
How can I learn to work with quantum algorithms in Java?
You can download and master Strange , the open source quantum computer simulator in Java. Strange allows you to simulate a quantum algorithm by creating a series of qubits and applying several quantum gates to them.
As a simple example, let's create two qubits, q [0] and q [1], so that initially both of them are in state 0. Then we apply two simple gates to each of the qubits, so that graphically this operation corresponds to fig. 7.
The first qubit will first go to the Pauli-X valve, and then to the Hadamard valve. The Pauli-X valve will transfer it from the state | 0> to | 1>, and the Hadamard valve will translate it into a superposition with equal probabilities | 0> and | 1>. Therefore, if we complete the entire sequence 1000 times and measure the first qubit 1000 times at the end of this cycle, then on average we can expect that it will have a value of 0 in 500 cases and a value of 1 in 500 cases. The
second qubit is even simpler. We start with the Identity gate, which does not change the behavior of the qubit, and then pass it to the Pauli-X gate, changing its value from 0 to 1.

Fig. 7. An example of a quantum algorithm that can be simulated using Strange.
To make sure our reasoning is correct, you can create a simple quantum program using Strange.
public static void main(String[] args) {
Program p = new Program(2);
Step s = new Step();
s.addGate(new X(0));
p.addStep(s);
Step t = new Step();
t.addGate(new Hadamard(0));
t.addGate(new X(1));
p.addStep(t);
SimpleQuantumExecutionEnvironment sqee = new SimpleQuantumExecutionEnvironment();
Result res = sqee.runProgram(p);
Qubit[] qubits = res.getQubits();
Arrays.asList(qubits).forEach(q -> System.out.println("qubit with probability on 1 = "+q.getProbability()+", measured it gives "+ q.measure()));
}In this application, a quantum program with two qubits is created:
Program p = new Program(2);As part of this program, we go through two stages. In the first step, apply the Pauli-X valve to q [0]. We do not apply the valve to q [1], and thus imply that it will work with the Identity valve. Add this step to the program:
Step s = new Step();
s.addGate(new X(0));
p.addStep(s);Then we pass to the second stage, where we apply the Hadamard valve to q [0] and the Pauli-X valve to q [1]; add this step to the program:
Step t = new Step();
t.addGate(new Hadamard(0));
t.addGate(new X(1));
p.addStep(t);So, our program is ready. Now let's do it. A quantum simulator is built into Strange, however, Strange can also use a cloud service to run programs in some kind of cloud, for example, in Oracle Cloud .
In the following example, we use a simple built-in simulator, run the program and get the resulting qubits:
SimpleQuantumExecutionEnvironment sqee = new SimpleQuantumExecutionEnvironment();
Result res = sqee.runProgram(p);
Qubit[] qubits = res.getQubits();Before we measure the qubits (and lose all the information), we display the probabilities. Now measure the qubits and look at the values:
Arrays.asList(qubits).forEach(q -> System.out.println("qubit with probability on 1 = "+q.getProbability()+", measured it gives "+ q.measure()));By launching this application, we get the following conclusion: Note: for the first qubit, the value 0 can also be measured, as we expected. If you run this program many times, then the value of the first qubit on average will be 0 in half the cases and 1 in half the cases.
qubit with probability on 1 = 0.50, measured it gives 1
qubit with probability on 1 = 1, measured it gives 1Is that all you need to know about quantum computing?
Of course not. Here we did not touch upon a number of important concepts, in particular, we did not discuss the intricacies that ensure the interaction between two qubits, even if physically they are very far from each other. We did not talk about the most famous quantum algorithms, among them the Shore algorithm, which allows decomposing integers into prime factors. We also ignored a number of mathematical and physical facts, in particular, did not take into account that in the superposition | x> = a | 0> + b | 1>, both numbers a and b can be complex.
However, the main purpose of this article was to give you the impression of quantum computing and to understand how they fit into the future of software development.
