The fourth level of Max Tegmark's multi-universe
Almost 10 years ago I read an article by Max Tegmark , a brilliant physicist and philosopher, and found in it the answers to many questions that have tormented me all my life. The article is amazing, for two months I went under the impression of it. Unfortunately, this is Longrid, and also in English. Therefore, I decided not to even translate it - the translation would still be too long for Habr, but at least set out the main idea in the order that it seems logical to me, and removing unnecessary details (Max forgive me!)

What it is? This formula is unlikely to tell you something. And if I write it like this:
Then you will immediately recognize Newton’s law in it. Of course, both formulas are equivalent, we are just used to the fact that the force is denoted by F, mass m, moreover, we mean that the matter takes place in three-dimensional space, that the bodies have coordinates, etc. That is, the theory has two components: formulas and blah blah around them. Max calls the second component verbal baggage .
Consider the tree of existing theories:

At the very bottom is sociology, where there are almost no formulas, but many words. Moving upstairs, we encounter more and more complicated mathematics. But with words it’s getting worse and worse: try to find out from a scientist who is engaged in fundamental physics what time is. It’s obvious to you that time is a sequence of eventsand it flows forward . The more you know and the deeper you go, the less obvious it becomes. The description of what time is, more and more collapses to the fact that time is the letter t , which is involved in such and such equations.
So, Max notes that:
As you move to an increasingly fundamental level, mathematics becomes more complex, and luggage begins to degenerate more and more. In the limit, Max suggests, the TOE (Theory of Everything - General Theory of Everything) has no baggage . So, TOE consists only of formulas .
This is the first ingredient. Remember him.
How is this even possible? Physics is trying to find equations for our world, based on observations and experimental data. Max suggests looking at “ Physics from Scratch, ” “ Physics from Scratch, ” you ask the equation, what kind of world do you get?
We can set the laws of the world ... well, for example, the game "life". Can we do without a verbal description? How, for example, to say that the space of cells is two-dimensional? Through equations, by indicating a power law, how quickly the number of cells grows no further than the distance N. Another example, equations of string theoryconverge only if the dimension of space is 10, 11, or 26. It may seem to formulate axiomatically physics at first, but mathematicians have succeeded in creating axiomatic theories (and worlds). Take, for example, Peano's axiomatics . These are pure formulas; it does not explain what a “number" is, what it means to add or multiply.
What do we have? We have (will) a TOE describing ALL that exists.
One second ... And what does “describing” mean? For example, mechanics describes the motion of bodies. But we know that all this is possible thanks to a bunch of simplifications: bodies are not material points, there is air resistance, friction, etc. There are formulas that describe reality, but we know that the real world is different from the ideal, described by formulas.
But in the case of TOE, this is not so: any, absolutely any physical aspect of reality is described by formulas - or it is not TOE. What is the difference between theory and reality in this case, if they are absolutely equivalent?
Max claims that in the case of TOE, mathematics does not describe reality, and mathematics is reality. If you suddenly disagree, the opposite would mean that there are equations with their solutions, there is exactly the same world that is completely subject to the indicated formulas, but also real . In this case, the words “ still real ” are verbal baggage in its pure form, which we abandoned above, such a modern anima sola of physics. Thus, we are forced to admit that at the fundamental level, physics and mathematics are one and the same.
Max was not the first with such ideas. Hawking himself posed the question: “ But what exactly does the flame breathe into these equations, creating the universe?” ” “ What is it that breathes fire into the equations and makes a universe for them to describe? ”

If we said that our universe is special because it exists , we would again be thrown back a step back to the concept of anima sola. No, nothing blows the flame into our formulas. It would be strange if all axiomatic systems of mathematics would be divided into two unequal classes: systems for which universes exist and systems that are unlucky. This contradicts the entire hypothesis of the mathematical universe.
All this can be explained only as follows: if there is no anima sola, thenall axiomatic systems are equal and the universe corresponds to each axiomatic system. Yes, most of the systems are most likely trivial, and perhaps most axiomatics do not give the opportunity to develop (that is, appear in solutions) complex, non-trivial systems and, especially, life.
“Physics vice versa” is still waiting for its future researchers. I would give dearly to find out if our universe is the simplest of those where intelligent life is possible or not.
Interestingly, after the first step (TOU does not have luggage), the second step (mathematics and physics are one and the same) and the third step (each axiomatics creates a universe) were forced. That's how far we got.
And why does the universe even exist?
Answer: because it can exist.
When did these structures arise and why did they arise?
Mathematical structures do not exist in time and space. They just exist.
Are we an emulation?
Not. For the existence of mathematical structures, no machine is needed to “count” them. The number 19 is simple, regardless of whether or not there is a computer that all the time tries to divide it in a cycle, checking for simplicity
How can we postulate something that we cannot fundamentally verify? Max expects this criticism. In fact, this is not the first time we do this. We have long been accustomed to the concept of the multiverse.
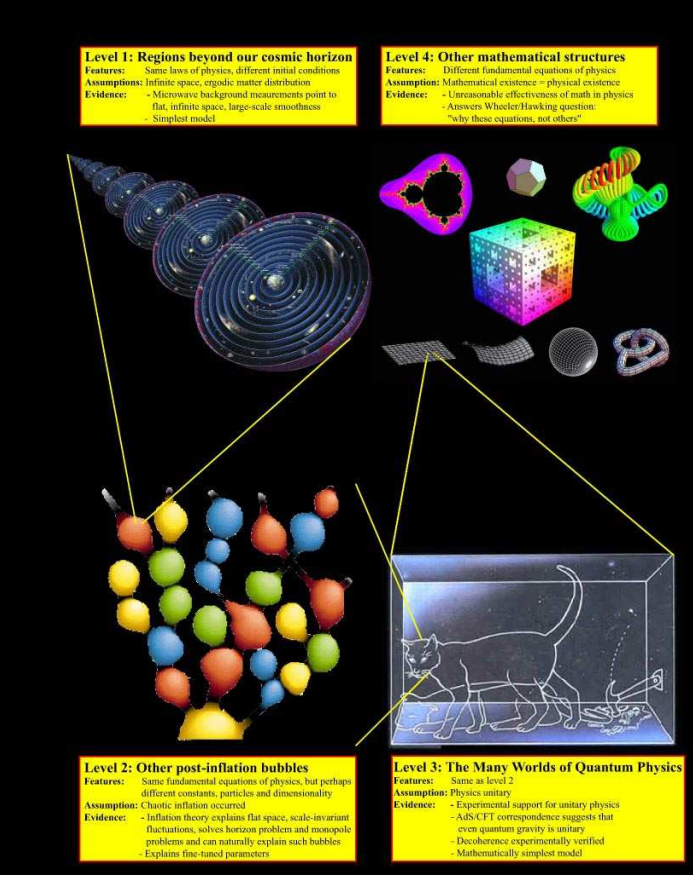
At level 1, we are talking about areas of the universe that are moving so quickly away from us due to expansion that they will never again be causally connected with us. Nevertheless, not a single cosmologist will turn his tongue to say that there is nothing there, because we cannot fly there.
At level 2, we are talking about other “bubbles” in the theory of eternal inflation, where, perhaps, under the same laws of physics, other initial conditions and other physical constants
Level 3 is formed by alternative universes of the Multiverse inEverett’s interpretation . This will be a separate article.

We are forced to accept the existence of level 4 , corresponding to other mathematical universes that we have yet to study (theoretically).

Formulas and Baggage
What it is? This formula is unlikely to tell you something. And if I write it like this:
Then you will immediately recognize Newton’s law in it. Of course, both formulas are equivalent, we are just used to the fact that the force is denoted by F, mass m, moreover, we mean that the matter takes place in three-dimensional space, that the bodies have coordinates, etc. That is, the theory has two components: formulas and blah blah around them. Max calls the second component verbal baggage .
Consider the tree of existing theories:

At the very bottom is sociology, where there are almost no formulas, but many words. Moving upstairs, we encounter more and more complicated mathematics. But with words it’s getting worse and worse: try to find out from a scientist who is engaged in fundamental physics what time is. It’s obvious to you that time is a sequence of eventsand it flows forward . The more you know and the deeper you go, the less obvious it becomes. The description of what time is, more and more collapses to the fact that time is the letter t , which is involved in such and such equations.
So, Max notes that:
As you move to an increasingly fundamental level, mathematics becomes more complex, and luggage begins to degenerate more and more. In the limit, Max suggests, the TOE (Theory of Everything - General Theory of Everything) has no baggage . So, TOE consists only of formulas .
This is the first ingredient. Remember him.
Physics “On the contrary”
How is this even possible? Physics is trying to find equations for our world, based on observations and experimental data. Max suggests looking at “ Physics from Scratch, ” “ Physics from Scratch, ” you ask the equation, what kind of world do you get?
We can set the laws of the world ... well, for example, the game "life". Can we do without a verbal description? How, for example, to say that the space of cells is two-dimensional? Through equations, by indicating a power law, how quickly the number of cells grows no further than the distance N. Another example, equations of string theoryconverge only if the dimension of space is 10, 11, or 26. It may seem to formulate axiomatically physics at first, but mathematicians have succeeded in creating axiomatic theories (and worlds). Take, for example, Peano's axiomatics . These are pure formulas; it does not explain what a “number" is, what it means to add or multiply.
Description vs Equivalence.
What do we have? We have (will) a TOE describing ALL that exists.
One second ... And what does “describing” mean? For example, mechanics describes the motion of bodies. But we know that all this is possible thanks to a bunch of simplifications: bodies are not material points, there is air resistance, friction, etc. There are formulas that describe reality, but we know that the real world is different from the ideal, described by formulas.
But in the case of TOE, this is not so: any, absolutely any physical aspect of reality is described by formulas - or it is not TOE. What is the difference between theory and reality in this case, if they are absolutely equivalent?
Max claims that in the case of TOE, mathematics does not describe reality, and mathematics is reality. If you suddenly disagree, the opposite would mean that there are equations with their solutions, there is exactly the same world that is completely subject to the indicated formulas, but also real . In this case, the words “ still real ” are verbal baggage in its pure form, which we abandoned above, such a modern anima sola of physics. Thus, we are forced to admit that at the fundamental level, physics and mathematics are one and the same.
Formulas and Flames
Max was not the first with such ideas. Hawking himself posed the question: “ But what exactly does the flame breathe into these equations, creating the universe?” ” “ What is it that breathes fire into the equations and makes a universe for them to describe? ”

If we said that our universe is special because it exists , we would again be thrown back a step back to the concept of anima sola. No, nothing blows the flame into our formulas. It would be strange if all axiomatic systems of mathematics would be divided into two unequal classes: systems for which universes exist and systems that are unlucky. This contradicts the entire hypothesis of the mathematical universe.
All this can be explained only as follows: if there is no anima sola, thenall axiomatic systems are equal and the universe corresponds to each axiomatic system. Yes, most of the systems are most likely trivial, and perhaps most axiomatics do not give the opportunity to develop (that is, appear in solutions) complex, non-trivial systems and, especially, life.
“Physics vice versa” is still waiting for its future researchers. I would give dearly to find out if our universe is the simplest of those where intelligent life is possible or not.
Answers to some questions
Interestingly, after the first step (TOU does not have luggage), the second step (mathematics and physics are one and the same) and the third step (each axiomatics creates a universe) were forced. That's how far we got.
And why does the universe even exist?
Answer: because it can exist.
When did these structures arise and why did they arise?
Mathematical structures do not exist in time and space. They just exist.
Are we an emulation?
Not. For the existence of mathematical structures, no machine is needed to “count” them. The number 19 is simple, regardless of whether or not there is a computer that all the time tries to divide it in a cycle, checking for simplicity
And is this generally like science or fantasies?
How can we postulate something that we cannot fundamentally verify? Max expects this criticism. In fact, this is not the first time we do this. We have long been accustomed to the concept of the multiverse.

At level 1, we are talking about areas of the universe that are moving so quickly away from us due to expansion that they will never again be causally connected with us. Nevertheless, not a single cosmologist will turn his tongue to say that there is nothing there, because we cannot fly there.
At level 2, we are talking about other “bubbles” in the theory of eternal inflation, where, perhaps, under the same laws of physics, other initial conditions and other physical constants
Level 3 is formed by alternative universes of the Multiverse inEverett’s interpretation . This will be a separate article.

We are forced to accept the existence of level 4 , corresponding to other mathematical universes that we have yet to study (theoretically).
