Graphics Optimization. Interesting Concave Hull
At one point, during the development of the game, I was faced with the issue of performance on modern PCs. Our modeller has a powerful modern red computer assembly. But he had our project terribly slow, loading one core of the processor.
The reason is simple - there are a lot of cores in new processors, but in fact they are less productive in single-threaded applications. At that time, I had a render in one stream. But in fact, the reasons were not so much in this. And in the process of searching for a problem, I decided to count how many polygons are present in the scene:
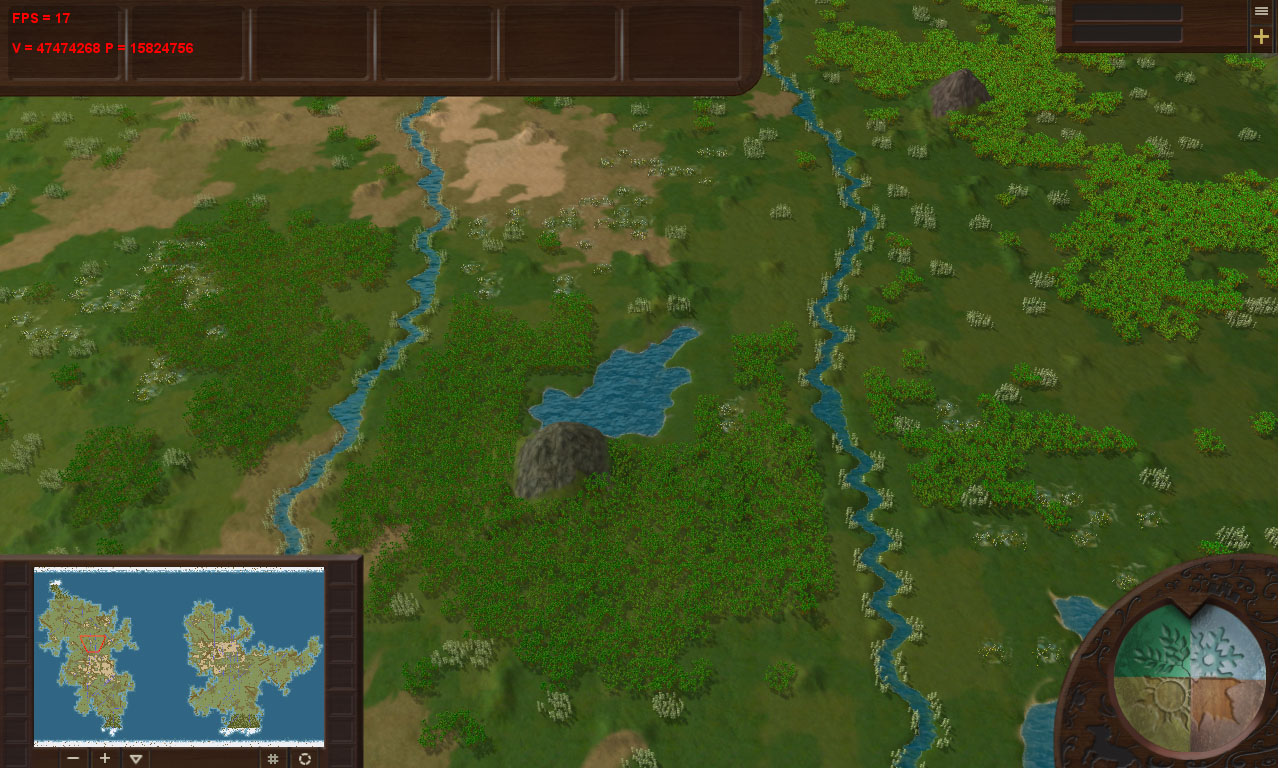
On the middle game map, at the maximum distance and with a large cluster of palm trees - 15 824 756 triangles! Almost 16 million! Huge number.
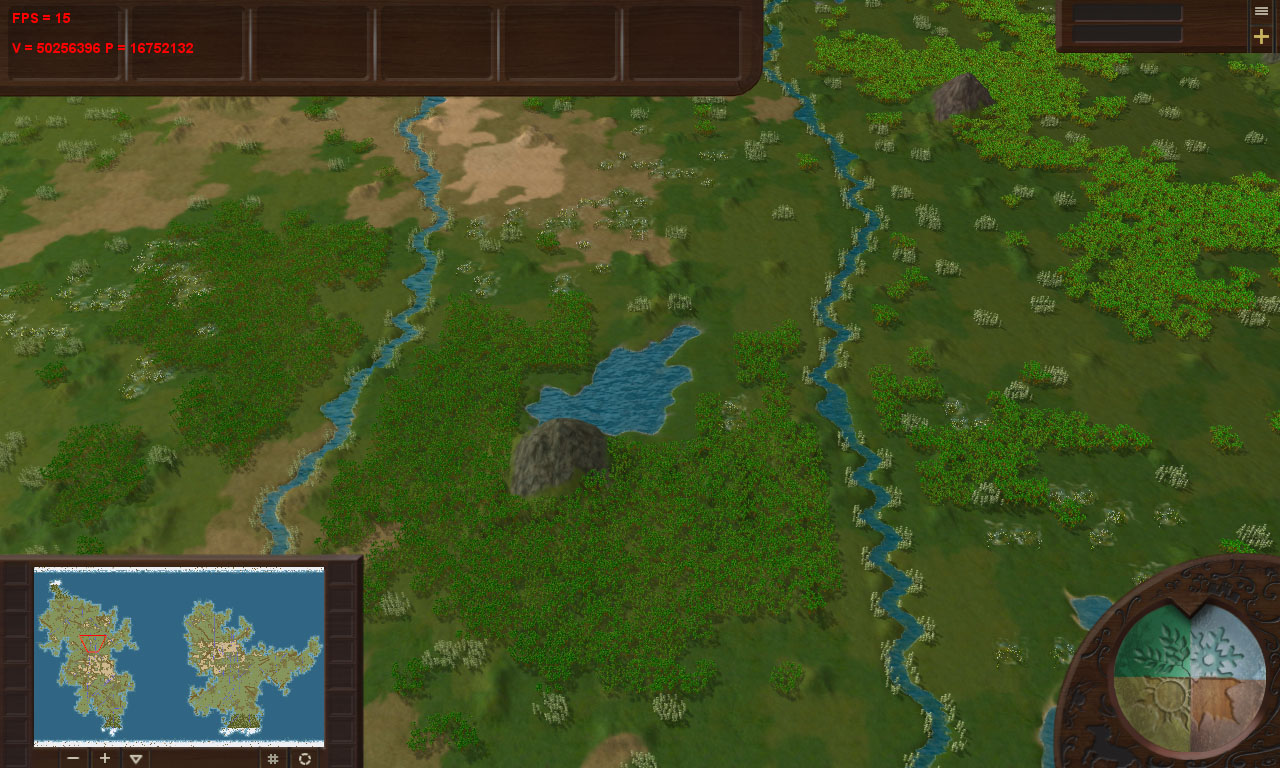
Having played a bit with the map generator, I managed to find a place with 16.75 million:
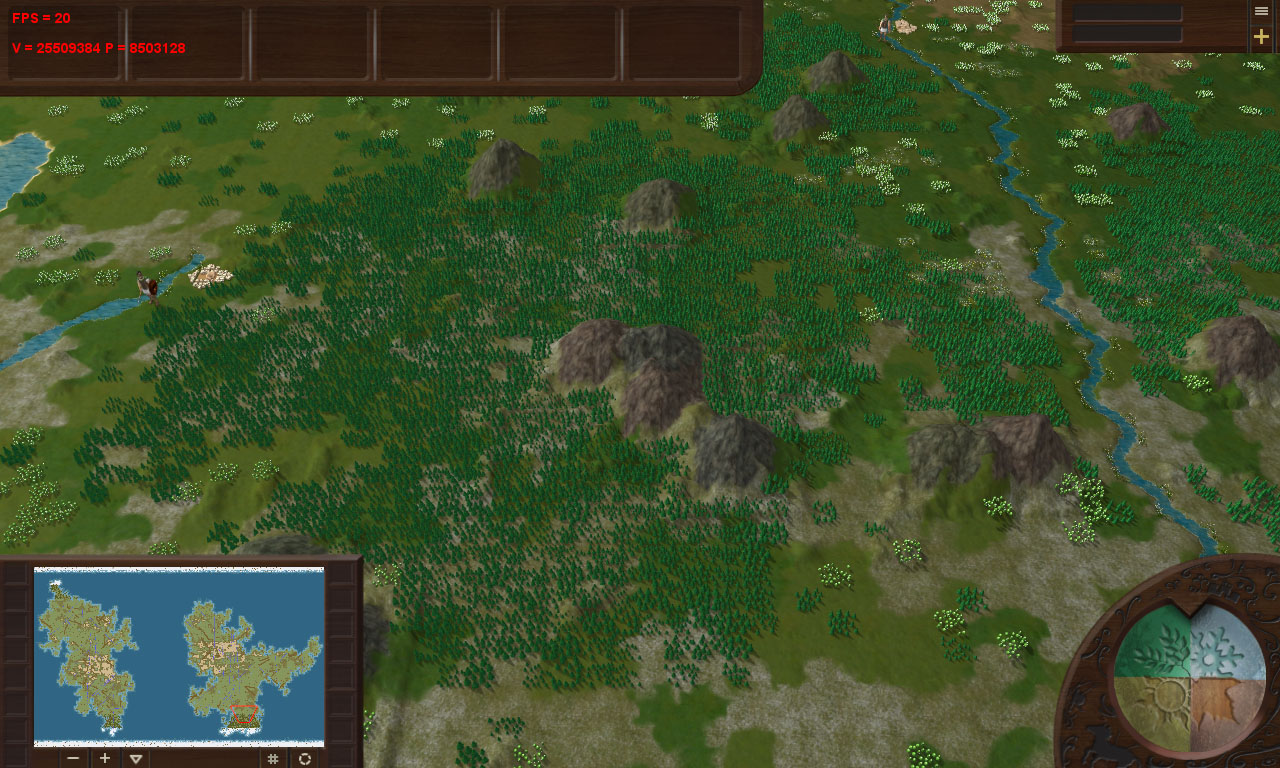
Although, like this, a place with Christmas trees gave only 8.5 million triangles:
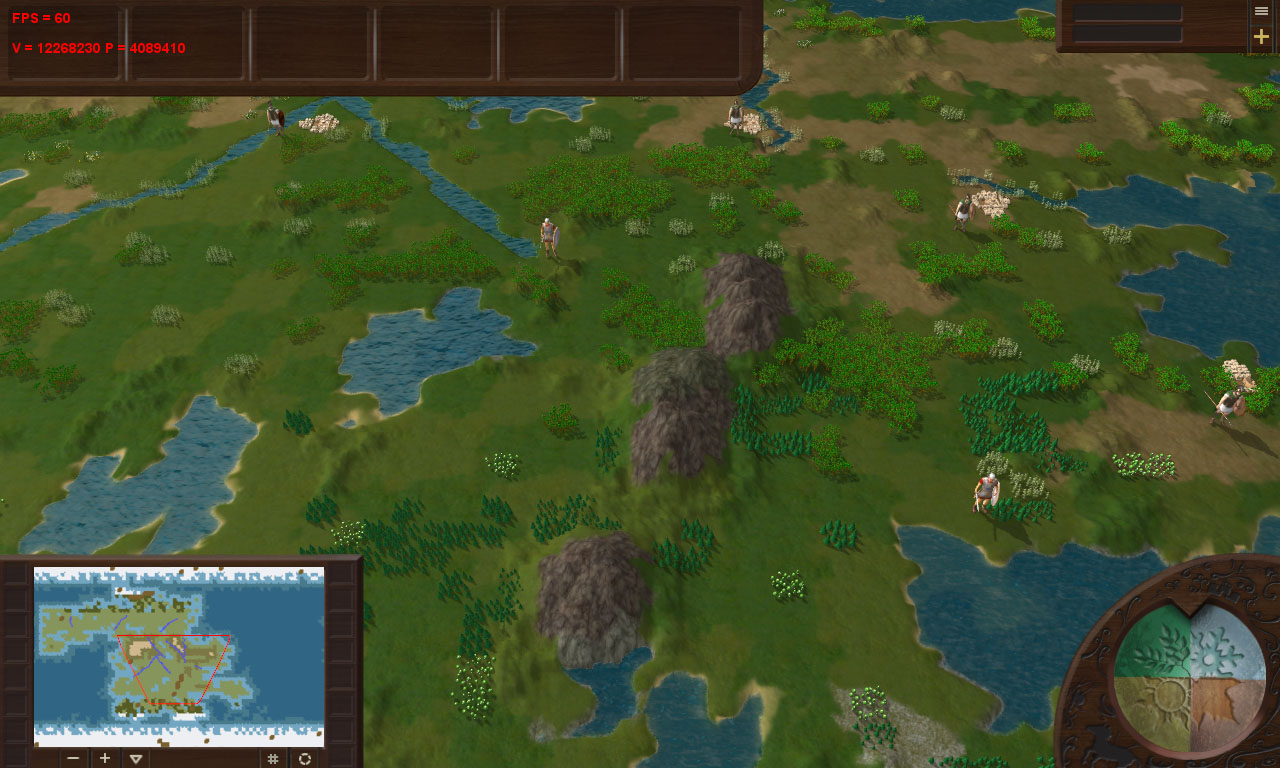
On average, the scene consisted of ~ 4 million:
In general, I was glad that my render copes with such a huge number of triangles, but their number was excessive. The decision was on the surface:
For those who may not be interested in the first item of our optimization program, for example, experienced specialists, I recommend to move safely to the second part.
In our engine, the vegetation is drawn in "packs", the whole landscape is divided into tiles and sub-files, the minimum pack is one subtail.

One pack is one mesh, as reducing the number of meshes significantly reduces the number of CPU-> GPU calls.

Initially, our Christmas trees consisted of truncated cones, going to full cones, managed to remove a couple of extra triangles: The

cherry on the cake was the decision to remove the trunks from the trees, since with our camera angle they were simply not visible.
As a result, we managed to reduce the number of polygons, on one package of trees, by an average of 40%. There are almost no differences:

With palm trees it was more difficult, but packs of 5000 to 6000 polygons needed to be corrected. How to achieve the massiveness and density of the jungle? The high density of the jungle was achieved due to the large number of palm trees:

We decided to simplify the palm trees and introduce the second tier of vegetation, which allowed us to maintain the apparent density and achieve the desired 600 - 700 polygons per pack.

Reducing the number of polygons 10 times - an excellent result.

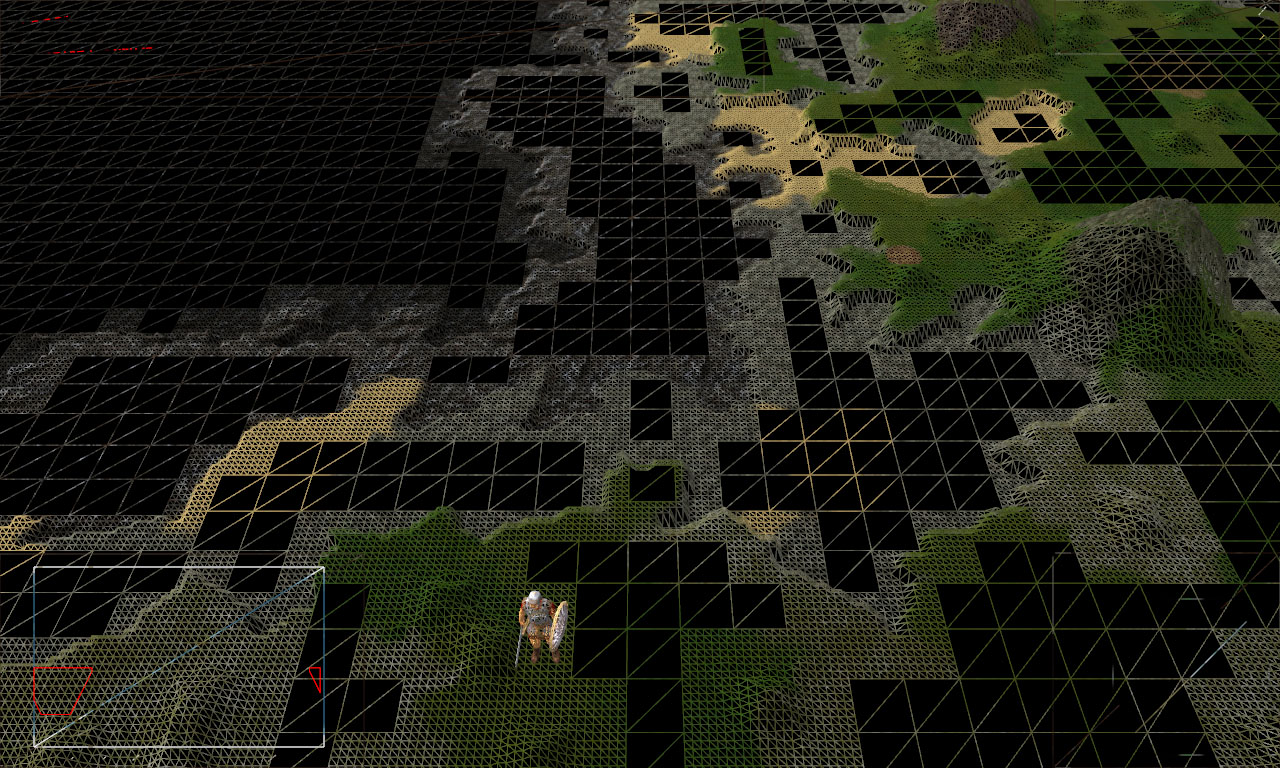
Initially, the landscape grid had the form:

The screenshot shows smooth areas of the landscape, these are tiles of meadows, plains, and other smooth surfaces. Minor unevenness of the landscape decided to remove. Thus, he increased the area of identical tiles in height. Not a tricky test of all the vertices of tiles and subtypes for equality in height, I was able to achieve this result:
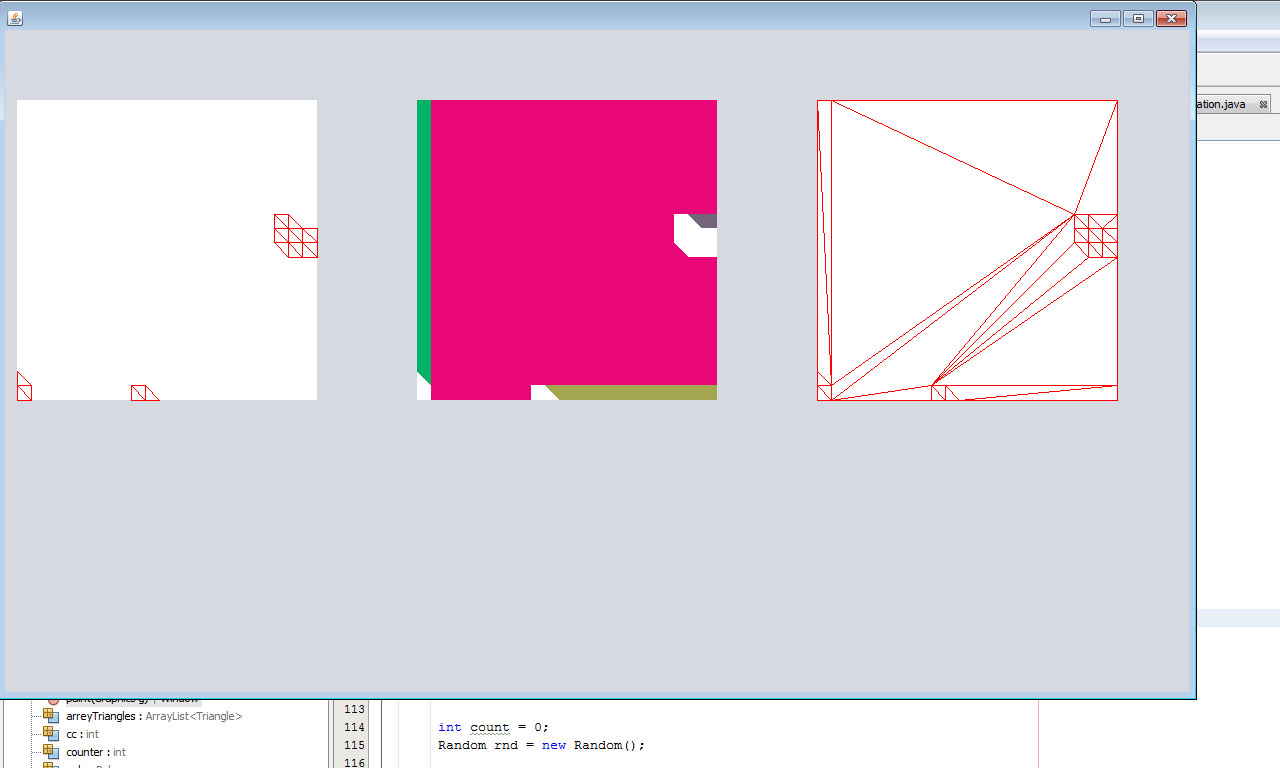
There were still flat places that could be optimized, and I began to build polygons from those triangles that had the same height. The tile was taken and all its triangles were sorted into an array of unequal in height triangles and a list of arrays consisting of equal in height and adjacent triangles.

In the above example, it turned out: 1 array of triangles not subject to change, since they were all of different heights (red triangles) and a list consisting of two arrays of triangles with the same height (arrays are filled with color).
Now the task was to find a convex-concave contour from the array of triangles (Concave Hull), and the set of triangles could have holes. Earlier in my work I came across convex contours (Convex Hull), there were no problems with them, I already used the Graham scan algorithm. But with the construction of the Concave Hull there were problems ... Information on this topic found on the Internet turned out to be quite difficult. I had to write the implementation of algorithms from scratch. I will not lie if I say that I have read about a dozen different dissertations on this topic. But all the proposed algorithms gave an approximate result with some error. After a week of torment and pain, I got the idea of my own algorithm.
I tried to build a contour over a set of triangle vertices, i.e. I transferred an array of triangles to an array of vertices and built a shell over them. But for my task it was not required. According to my conclusions, constructing a shell directly in triangles was simpler, and the accuracy of the concave hull was 100%.
Initially, I wanted to put here the wrapper of the source code of the algorithm, but it seems easier to describe it in two words: Basis - the rule: if the vertex of the triangle enters four or less triangles, then one of the edges that forms the vertex lies on the border. Next, a list of such edges is formed taking into account the removal of identical edges. We find the edge with the smallest X and Y and from it we start the passage / sorting of edges with the incidental addition of unique vertices to the list. This list will be the envelope of the set of triangles. The only thing in the final is to remove the collinear points from the list.
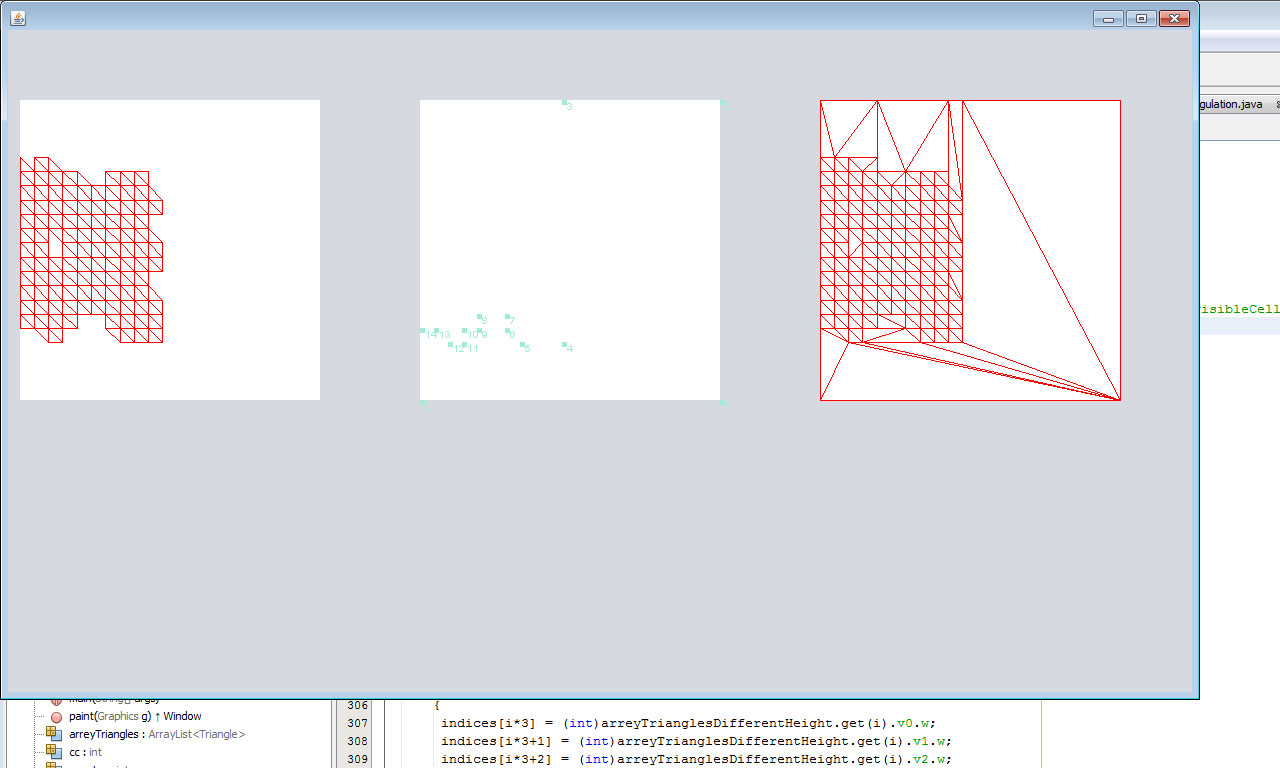
As a result of this, I could build the Concave Hull of almost any complexity. This algorithm did not fit the set with holes, but I went around this by simply dividing this set into two halves by hole. Then I received a contour and triangulated it:
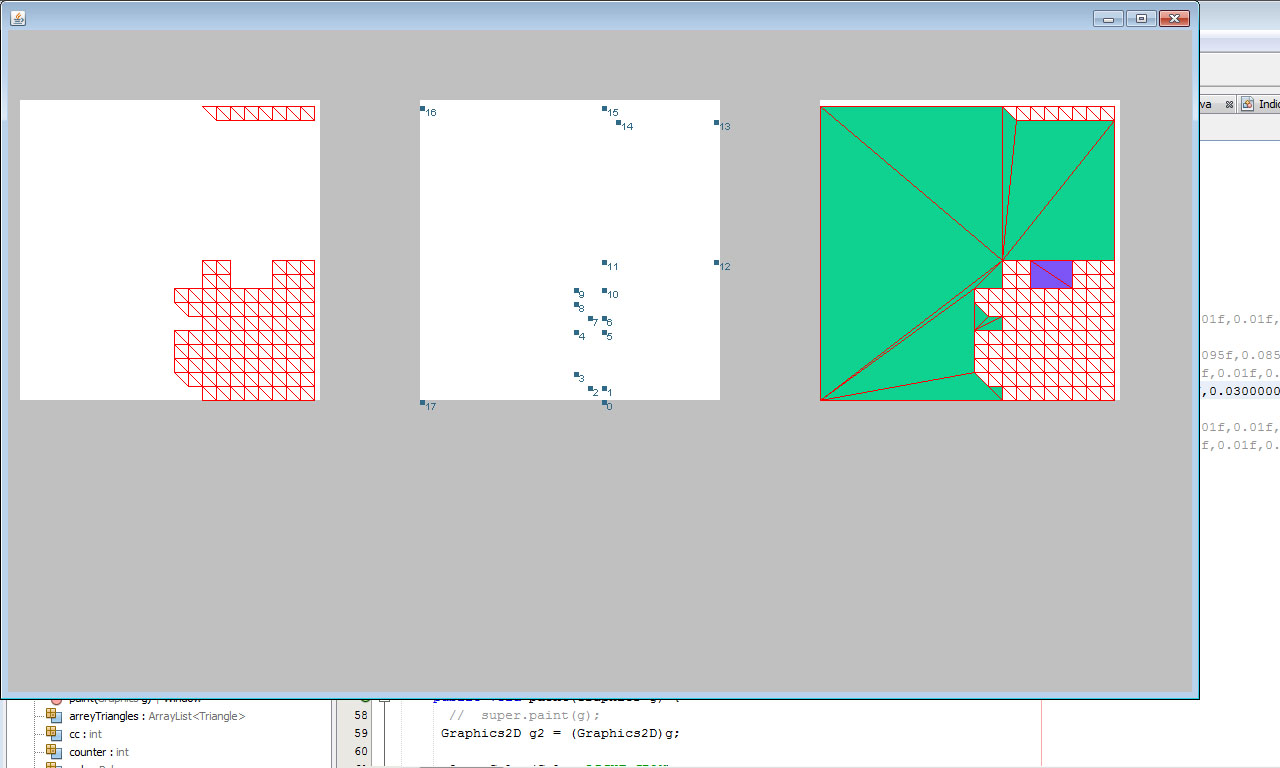
Everything turned out great:

But in the end, I was upset with the result. The algorithm developed by me gave a tangible increase in performance when rendering the scene, since the number of polygons on average was reduced by 60 - 70%. But at the same time, card generation began to occur 10 times slower. The algorithm turned out to be very demanding on time costs.
It took three days to think about the light version of the algorithm for optimizing the polygonal grid of the landscape, which gave these results:

Now the calculations of data for optimization have become not noticeable against the background of map generation, and the number of polygons has decreased on average by 40-50%.
This article is a trial and superficial. If anyone is interested in the topic of game development, I am ready to continue and expand the article with a speculation of concrete steps, decisions and future plans. Also, I think you will be interested in the topic of building a multithreaded Open GL application developed in Java, which I will try to describe in the next article.
The reason is simple - there are a lot of cores in new processors, but in fact they are less productive in single-threaded applications. At that time, I had a render in one stream. But in fact, the reasons were not so much in this. And in the process of searching for a problem, I decided to count how many polygons are present in the scene:

On the middle game map, at the maximum distance and with a large cluster of palm trees - 15 824 756 triangles! Almost 16 million! Huge number.
Having played a bit with the map generator, I managed to find a place with 16.75 million:

Although, like this, a place with Christmas trees gave only 8.5 million triangles:

On average, the scene consisted of ~ 4 million:

In general, I was glad that my render copes with such a huge number of triangles, but their number was excessive. The decision was on the surface:
- Optimize the number of polygons in the models.
- Optimize the polygonal grid of the landscape.
- The implementation of a multi-threaded render.
For those who may not be interested in the first item of our optimization program, for example, experienced specialists, I recommend to move safely to the second part.
1. Optimization of the number of polygons in models
In our engine, the vegetation is drawn in "packs", the whole landscape is divided into tiles and sub-files, the minimum pack is one subtail.

One pack is one mesh, as reducing the number of meshes significantly reduces the number of CPU-> GPU calls.

Initially, our Christmas trees consisted of truncated cones, going to full cones, managed to remove a couple of extra triangles: The

cherry on the cake was the decision to remove the trunks from the trees, since with our camera angle they were simply not visible.
As a result, we managed to reduce the number of polygons, on one package of trees, by an average of 40%. There are almost no differences:

With palm trees it was more difficult, but packs of 5000 to 6000 polygons needed to be corrected. How to achieve the massiveness and density of the jungle? The high density of the jungle was achieved due to the large number of palm trees:

We decided to simplify the palm trees and introduce the second tier of vegetation, which allowed us to maintain the apparent density and achieve the desired 600 - 700 polygons per pack.

Reducing the number of polygons 10 times - an excellent result.

2. Optimization of the polygonal grid of the landscape
Initially, the landscape grid had the form:

The screenshot shows smooth areas of the landscape, these are tiles of meadows, plains, and other smooth surfaces. Minor unevenness of the landscape decided to remove. Thus, he increased the area of identical tiles in height. Not a tricky test of all the vertices of tiles and subtypes for equality in height, I was able to achieve this result:

There were still flat places that could be optimized, and I began to build polygons from those triangles that had the same height. The tile was taken and all its triangles were sorted into an array of unequal in height triangles and a list of arrays consisting of equal in height and adjacent triangles.

In the above example, it turned out: 1 array of triangles not subject to change, since they were all of different heights (red triangles) and a list consisting of two arrays of triangles with the same height (arrays are filled with color).
Now the task was to find a convex-concave contour from the array of triangles (Concave Hull), and the set of triangles could have holes. Earlier in my work I came across convex contours (Convex Hull), there were no problems with them, I already used the Graham scan algorithm. But with the construction of the Concave Hull there were problems ... Information on this topic found on the Internet turned out to be quite difficult. I had to write the implementation of algorithms from scratch. I will not lie if I say that I have read about a dozen different dissertations on this topic. But all the proposed algorithms gave an approximate result with some error. After a week of torment and pain, I got the idea of my own algorithm.
I tried to build a contour over a set of triangle vertices, i.e. I transferred an array of triangles to an array of vertices and built a shell over them. But for my task it was not required. According to my conclusions, constructing a shell directly in triangles was simpler, and the accuracy of the concave hull was 100%.
Initially, I wanted to put here the wrapper of the source code of the algorithm, but it seems easier to describe it in two words: Basis - the rule: if the vertex of the triangle enters four or less triangles, then one of the edges that forms the vertex lies on the border. Next, a list of such edges is formed taking into account the removal of identical edges. We find the edge with the smallest X and Y and from it we start the passage / sorting of edges with the incidental addition of unique vertices to the list. This list will be the envelope of the set of triangles. The only thing in the final is to remove the collinear points from the list.
As a result of this, I could build the Concave Hull of almost any complexity. This algorithm did not fit the set with holes, but I went around this by simply dividing this set into two halves by hole. Then I received a contour and triangulated it:



Everything turned out great:

But in the end, I was upset with the result. The algorithm developed by me gave a tangible increase in performance when rendering the scene, since the number of polygons on average was reduced by 60 - 70%. But at the same time, card generation began to occur 10 times slower. The algorithm turned out to be very demanding on time costs.
It took three days to think about the light version of the algorithm for optimizing the polygonal grid of the landscape, which gave these results:

Now the calculations of data for optimization have become not noticeable against the background of map generation, and the number of polygons has decreased on average by 40-50%.
This article is a trial and superficial. If anyone is interested in the topic of game development, I am ready to continue and expand the article with a speculation of concrete steps, decisions and future plans. Also, I think you will be interested in the topic of building a multithreaded Open GL application developed in Java, which I will try to describe in the next article.
