Why do some notes sound harmoniously together

Have you ever wondered why some notes are more suited to each other than others? How are the frequencies of their waves connected? Why do the notes of one key sound “good”? Why do the notes in the chord sound “good”?

The answer to this question is related to the concept of “consonance” (ie, “consonance”) and modern science, psychoacoustics. Consonance is a consonant, harmonious sound, and dissonance, on the contrary, is dissenting or restless.

First of all, it is necessary to distinguish between pure tones, which are ordinary sine waves, and real tones, which are reproduced by musical instruments. Real tones, in fact, consist of harmonic overtones with different amplitudes. Thus, each note played on any instrument is a complex sound consisting of a fundamental tone and a large number of overtones.

An overtone is any natural frequency above the fundamental, and those overtones whose frequencies refer to the fundamental frequency as integers are called harmonics. In this case, the fundamental tone is considered the first harmonic. It turns out that the frequency values ​​of each harmonic relate to the fundamental tone as follows: f, 2f, 3f, 4f, ....

Harmonic frequencies also relate to each other as integers and form the main musical intervals: 2: 1 is an octave, 3: 2 is a quint, 4: 3 is a quart, etc. In different musical cultures and in different periods of time, the relation to the consonance and dissonance intervals was different. At the time of Pythagoras, the octave, fifth and fourth were considered consonant intervals, but in the 13th century a third joined them. All this is due to a change in musical tastes.

Ian Johnston wrote the book Measured Tones, which described the theory of consonance (musical consonance). In it, he compares the dissonance with seasonings, noting the fact that we all treat them differently. The structure of our ears and brain is different, therefore our concepts of “good sound” are also different.

Lucas Biewald, founder of CrowdFlower, agrees that “good sound” is a very subjective concept. He says that what songs we like depends on our culture, character, even mood.

Let's move away from personal preferences and go a little deeper into the physics of ongoing processes. “The most consonant will be notes with the same pitch. In other words, the salt of the small octave of the piano is consonant with the note of the salt (G) on the guitar, says Bivald. “Here is a graph of the sound wave played by a guitar string”:



A sound wave is a series of air vibrations that force small hair cells located in the inner ear of a person to vibrate at different frequencies. The sound we hear is the sum of these vibrations. To distinguish the frequencies hidden in this sound, we turn to mathematics for help and use the Fourier transform.



On the graph, we see that the note salt contains several frequencies. The lowest vibrational frequency of the string is 196 Hz. This frequency is called the fundamental. But we see that there are frequencies that exceed it two or more times - these are overtones or harmonics.

When Lucas Bivald sang a note of salt while striking the string G on the guitar, we got the following graph:



The appearance of the curve is different, but if you compare the frequency graphs, they will coincide.



Red dots indicate harmonics frequencies. Between them exactly 196 Hz, as in the previous case. Bivald says: "When I sing a note of salt and take it on a guitar, the air vibrations coming from the vocal cords and the instrument string affect the same hair cells in my ear."

Let's look at the graph that will turn out if you play a note of salt on a guitar, but an octave higher. It differs from the previous two.





If you look at the frequencies of harmonics, we will notice that the position of some of them coincides. As a result, in both cases, almost the same ear hair cells will vibrate. That is why we get the feeling that these are two identical notes, although they differ by one octave.

“In addition to the concept of an octave, we still have the concept of a fifth. The two notes that differ by a fifth are most consonant, ”says Bivald. The ratio between notes to and salt equals a fifth. Therefore, in the western musical tradition, most chords that are built from note to contain a note of salt. But why are they so fit together? Here are the frequencies of the note before played on a Bivald guitar.



Here, the frequencies of salt are marked in red, and the notes of do are marked in yellow. It can be seen that they do not always overlap, but since the main frequency of the note to refers to the main frequency of the note as 3/2, each third harmonic of the salt and every second harmonic of do coincide.

The notes that are most consonant with the do are considered to be the fa and the salt, since they are located at the distance of an ideal quart and an ideal fifth, respectively. Let's take a look at their harmonics.



The harmonics of salt and fa often overlap harmonics up to. However, the harmonics of salt and fa coincide an order of magnitude less often. That is why when we hear the notes salt + do and fa + do, they seem to us to be consonant, and when we hear the Fa + salt, we get a sense of dissonance. For this reason, these three notes are almost never taken at the same time. Now take a look at a more detailed graph:



It can be seen that before and mi there are many coinciding harmonics, therefore the notes of do, salt and mi form a chord in C major. Do and D sharp (E-flat) have the same number of harmonics, so the notes do, E-flat and salt form a chord in C minor. If the harmonics of notes do not correlate with each other, then with their simultaneous [notes] reproduction we hear a dissonance. For example, before and F sharp - they do not have overlapping harmonics. You can read more about this in another answer by Lucas Bivald.

There are other psychoacoustic effects that affect our perception of sound. Dissonance arises at the moment when we hear two sounds with almost identical, but still different, frequencies.



Over time, the phase shift increases:



We hear the sum of the blue and orange signals:



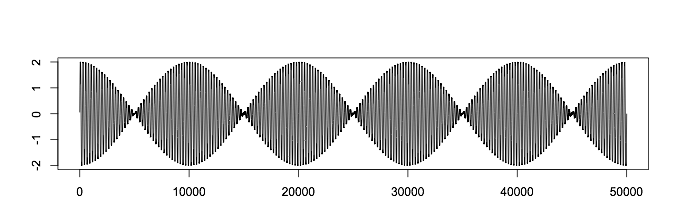
If we stretch the timeline, we get:



When the signals are in phase, they reinforce each other, and amplifying interference occurs. As the shift proceeds, weakening interference arises, and the signals begin to cancel each other until they are in strict antiphase.

Because of this, a pulsating sound arises that you probably heard (play the upset guitar or piano). For a Western listener, he seems discordant, but this technique is used in the music of some cultures.

PS Do not hesitate to comment from read-only-accounts, we will try to conduct moderation as quickly as possible, friends :)