Gamma correction

So, we calculated the colors of all the pixels in the scene, it's time to display them on the monitor. At the dawn of digital image processing, most monitors had cathode ray tubes (CRTs). This type of monitor had a physical feature: increasing the input voltage by a factor of two did not mean a twofold increase in brightness. The relationship between the input voltage and brightness was expressed by a power function, with a value of about 2.2, also known as monitor gamma .

This feature of monitors (by coincidence) is very similar to how people perceive brightness: with a similar (but inverse) power dependence. To better understand this, take a look at the following image:

The top line shows how the brightness is perceived by the human eye: when the brightness is increased 2 times (for example, from 0.1 to 0.2), the picture really looks like it is twice as bright: the changes are visible quite clearly. However, when we talk about the physical brightness of light, such as the number of photons emerging from a light source, the lower scale gives the correct picture. On it, doubling the value gives the correct brightness from a physical point of view, but since our eyes are more susceptible to changes in dark colors, this seems somewhat strange.

Since the upper version is more familiar to the human eye, monitors still use a power-law dependence when displaying colors, so that the original, in the physical sense, brightness values ​​are converted to non-linear brightness values ​​shown on the upper scale. This is mainly done because it looks better.

This feature of monitors really makes a picture better for our eyes, but when it comes to rendering graphics, there is one problem: all the color and brightness settings that we set in our applications are based on what we see on the monitor. And this means that all these parameters are actually non-linear. Take a look at the chart:

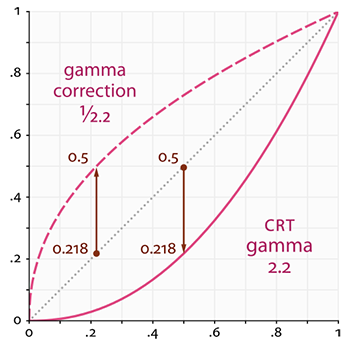
The gray line corresponds to the color values ​​in linear space; the solid red line represents the color space displayed by the monitor. When we want to get 2 times brighter color in linear space, we just take and double its value. For example, take a color vector$$, that is, a dark red color. If we doubled its value in linear space, it would become equal$$. On the other hand, when displayed, it will be converted to the color space of the monitor as$$as seen from the graph. This is where the problem arises: by doubling the dark red light in linear space, we actually make it more than 4.5 times brighter on the monitor!

Before this tutorial, we assumed that we worked in a linear space, but in fact we worked in the color space defined by the monitor, so all the colors and lighting variables that we set were not physically correct, but just looked right on our monitor specifically. Guided by this assumption, we (and artists) usually set the lighting values ​​brighter than they should be (because the monitor obscures them), which as a result makes most of the subsequent calculations in linear space incorrect. Also note that both graphs start and end at the same points, only intermediate colors are subject to dimming on the display.

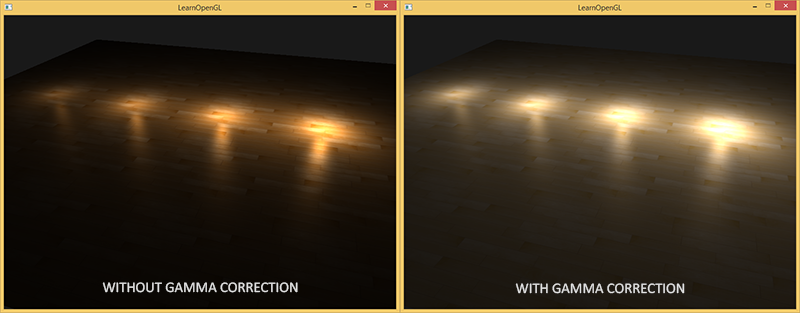
As I said, since the color values ​​are selected based on the image displayed by the monitor, all intermediate lighting calculations performed in linear space are physically incorrect. This becomes more apparent when we start using more advanced lighting algorithms. Just take a look at the image:

As you can see, the color values ​​(which we previously updated) using gamma correction are much better combined with each other, and dark areas become lighter, which increases their detail. There is much better image quality, with very minor modifications.

Without a properly tuned monitor gamut, lighting doesn't look right, and it will be quite difficult for artists to get realistic and beautiful results. To solve this problem it is necessary to apply gamma correction .

Gamma correction

The idea behind gamma correction is to apply the inverse of the gamma of the monitor to the final color before displaying it on the monitor. Again, look at the graph of the gamma curve at the beginning of this lesson, paying attention to another line, indicated by strokes, which is the inverse of the gamma curve of the monitor. We multiply the displayed color values ​​in linear space by this inverse gamma curve (make them brighter), and as soon as they are displayed on the monitor, the gamma curve of the monitor will be applied to them, and the resulting colors will again become linear. In fact, we make the intermediate colors brighter to balance their shading with the monitor.

We give one more example. Let's say we again have a dark red color$$. Before displaying this color on the monitor, we first apply the gamma correction curve to its components. The color values ​​in linear space, when displayed on the monitor, are raised to a power of approximately 2.2, so inversion requires us to raise the values ​​to a power of 1 / 2.2. Thus, the dark red color with gamma correction becomes$$ = $$ = $$. This corrected color is then displayed on the monitor, and as a result, it is displayed as$$ = $$. As you can see, when we use gamma correction, the monitor displays colors exactly as we set them in linear space in our application.

A gamma of 2.2 is the default value, which roughly expresses the average gamma of most displays. The color space resulting from this gamut is called the sRGB color space. Each monitor has its own gamma curves, but a value of 2.2 gives good results on most monitors. Because of these small differences, many games allow players to change the gamma setting.

There are two ways to apply gamma correction to your scenes:

• Use the built-in OpenGL sRGB support for the frame buffer.
• Perform gamma correction manually in fragment shaders.

The first option is simpler, but gives you less control. By setting the GL_FRAMEBUFFER_SRGB flag , you tell OpenGL that every next drawing command must perform gamma correction in the sRGB color space before writing data to the color buffer. After enabling GL_FRAMEBUFFER_SRGB, OpenGL will automatically perform gamma correction after starting each fragment shader for all subsequent frame buffers, including the default frame buffer.

Enabling the GL_FRAMEBUFFER_SRGB flag is done using a regular glEnable call :

glEnable(GL_FRAMEBUFFER_SRGB);

Now the color buffers rendered by you will have an adjusted gamut and, since this is done in hardware, it costs us nothing. The only thing you should remember with this approach (albeit with a different approach too) is that gamma correction converts colors from linear space to nonlinear, so it is very important that you perform gamma correction only at the last, final stage. If you apply gamma correction before the final output, all subsequent operations on these colors will work with incorrect values. For example, if you use multiple frame buffers, you probably want intermediate results to remain in linear space and only the last buffer apply gamma correction before sending it to the monitor.

The second approach requires a little more work, but it gives us full control over gamma operations. We apply gamma correction at the corresponding stage of the fragment shader, so gamma correction is applied to the resulting colors immediately before sending to the monitor:

void main()
{
    // делаем супер классное освещение
    [...]
    // применяем гамма-коррекцию
    float gamma = 2.2;
    FragColor.rgb = pow(fragColor.rgb, vec3(1.0/gamma));
}

The last line of code raises each component of the fragColor color to the power of $$, adjusting the result of this shader.

The problem with this approach is that you have to apply gamma correction for each fragment shader that contributes to the final output, so if you have a dozen fragment shaders for several objects, you will have to add a gamma correction code to each them. A more reasonable solution would be to add a post-processing step to your rendering cycle and apply gamma correction in the final quad as a last step. Then you will need to do this only once.

Actually, these 2 lines of code represent the technical implementation of gamma correction. Not too impressive, right? Wait, there are a couple more nuances that you should consider when gamma correction.

sRGB texture

Whenever you draw or edit an image on your computer, you choose colors based on what you see on the monitor. In fact, this means that all the images you created or edited are not in linear space, but in sRGB space, that is, doubling the dark red color on the screen, based on the brightness you perceive, is in fact not equal to doubling the red component of the color.

As a result, texture artists create them in the sRGB space, and if we use these textures in our application as they are, we must consider this. Before we applied gamma correction, this did not create problems, because the textures looked good in the sRGB space, and without gamma correction we also worked in this space, so the textures were displayed exactly as intended. However, now that we are displaying everything in linear space, the texture colors are incorrectly displayed, as seen in the following image:

The texture is overexposed, and this is because the gamma correction, in fact, was applied to it twice! Judge for yourself: when we create an image based on what we see on the monitor, we adjust the gamut of color values ​​of the image so that they look true on the screen. Since we are doing gamma correction again when rendering, the images become too bright.

To solve this problem, we need to make sure that texture artists work in linear space. However, since most artists do not even know what gamma correction is, and it is easier for them to work in the sRGB space, this is most likely not an option.

Another solution is to adjust or convert these sRGB textures back to linear space before doing any manipulation of their colors. We can do this as follows:

float gamma = 2.2;
vec3 diffuseColor = pow(texture(diffuse, texCoords).rgb, vec3(gamma));

However, doing this for each texture in sRGB is pretty troublesome. Fortunately, OpenGL gives us another solution to our problems by providing us with the internal texture formats GL_SRGB and GL_SRGB_ALPHA .

If we create a texture in OpenGL with any of the two specified sRGB texture formats, OpenGL will automatically convert their colors to linear space as soon as we use them, which will allow us to work correctly in linear space with all the color values ​​extracted from the texture. We can declare the texture as sRGB as follows:

glTexImage2D(GL_TEXTURE_2D, 0, GL_SRGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, image);

If you want to use the alpha component in your texture, you will need to designate the internal texture format as GL_SRGB_ALPHA .

You should be careful when declaring your textures as sRGB, since not all textures will be in sRGB space. Textures used to color objects, such as diffuse maps, are almost always found in sRGB space. The textures used to extract the lighting parameters, such as glare and normal maps, on the contrary, are almost always in linear space, so if you declare them as sRGB, the lighting will go. Be careful when specifying texture types.

By declaring our diffuse textures as sRGB, you will again get the expected result, but this time it’s enough to apply gamma correction only 1 time.

Attenuation

Another point that will be different when using gamma correction is the attenuation of lighting. In the real physical world, lighting fades out almost inversely with the square of the distance from the light source. In human language, this means that the light intensity decreases with distance from the light source, as shown below:

float attenuation = 1.0 / (distance * distance);

However, when using this equation, the damping effect is too strong, and the light spot gets a small radius, which does not look physically reliable. Therefore, we used other equations for the attenuation (we discussed this in the tutorial on the basics of lighting ), which give more tuning options, or even a linear version:

float attenuation = 1.0 / distance;

Without gamma correction, the linear option gives much more plausible results than the quadratic one, but when we turn on the gamma correction, the linear attenuation looks too weak, and physically correct quadratic unexpectedly gives better results. The figure below shows the differences between the options:

The reason for this difference is that the damping function of the light changes brightness, and since we did not display our scene in linear space, we chose the damping function, which looked best on our monitor, although it was not physically correct. When we used the quadratic attenuation function without gamma correction, in fact, it turned into$$when displayed on the monitor, which gave a much greater fading effect. This also explains why the linear version gives better results without gamma correction, because with it$$ = $$, which is much more like a physically correct relationship.

The more advanced attenuation function that we discussed in the basics of lighting is still useful in gamma correction scenes, as it gives much more control for more accurate implementation of the attenuation (but, of course, requires other parameters when using gamma correction).

I wrote a simple demo scene, the source code of which you can find here . By pressing the space bar, you can switch between scenes with and without gamma correction, each of which uses its own textures and attenuation functions. This is not the most impressive demonstration, but it shows how to apply these techniques.

To summarize: gamma correction allows you to work with colors in linear space. Since linear space is inherent in the physical world, most physical calculations will give better results, such as calculating the attenuation of light. Using gamma correction makes it much easier to achieve realistic results as the lighting techniques used become more complicated. That is why it is recommended that you immediately adjust the lighting settings to work with gamma correction.

Additional materials

• What every developer should know about gamma is a well-written, detailed article by John Novak about gamma correction.
• www.cambridgeincolour.com - more about gamma and gamma correction.
• blog.wolfire.com - David Rosen's blog post on the benefits of gamma correction when rendering graphics.
• renderwonk.com is some more practical considerations.

Original article