Blondes, monsters and addictions of artificial intelligence
The previous article left a feeling of understatement and two topics - blondes and monsters were not disclosed at all.
Let's try to fix it and start with the monsters.
It's no secret that most recognition systems use AI to identify potential candidates and we are also interested in checking how the numbers are.
Take the same mnist studied along and across and a convolutional network with accuracy: 0.9939.
The text is attached, you can check it (borrowed from keras.io and slightly modified).
Normal accuracy, if you add an epoch, you can also 0.995.
And now we’ll do a plastic surgery on the test set and cut each letter with a 7x7 knife.
This is 25% of the width and height - we will turn the numbers into monsters and see how our network recognizes them.
the result is pretty decent - accuracy: 0.7051. We randomly shredded each picture with a 7x7 window, despite the fact that they themselves were 28x28!
It can be seen on the slide that some of the numbers are completely crooked.
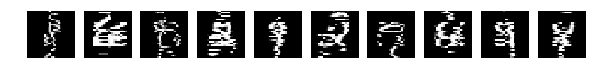
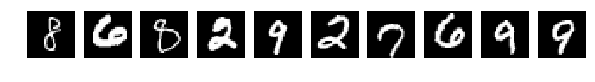
But the network copes, not very well, but copes. And if you train using different keras tricks for shifting and resizing, the result should be even better.
The conclusion is:
Monsters for AI do not pose a problem, the essence will be visible to him
And now to the main topic - blondes.
Let's just recolor the numbers, because they are greyscale, just rearrange the colors in them, just like in the previous article . But let's leave the trained network as it is. Those. we train the network on the original mnist without changing anything, and repaint the test sequence.
Let me remind you that the network is trained on normal mnist and gives accuracy: 0.9939.
But we will test blondes - “colored numbers”.

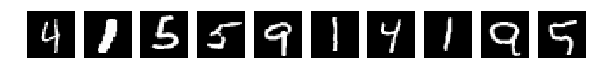
And then our super intellect suddenly showed some strange inclinations and addictions:
Result accuracy: 0.1634 discourages.
Everything is clearly visible on the test slides, understandable and clear, but the result of 0.1634 suggests that the network of them all, apparently, defines it as the same number and sometimes distinguishes it.
So, to hide from Big Brother, you don't need super plastic surgeons and shreds.
All you need to do is apply makeup correctly.
PS: I apologize for associations, blondes, monsters - this is not on purpose and did not want to offend anyone. Spring, Friday - I hope they will justify me.
Let's try to fix it and start with the monsters.
It's no secret that most recognition systems use AI to identify potential candidates and we are also interested in checking how the numbers are.
Take the same mnist studied along and across and a convolutional network with accuracy: 0.9939.
The text is attached, you can check it (borrowed from keras.io and slightly modified).
Normal accuracy, if you add an epoch, you can also 0.995.
Program text
from keras.datasets import mnist
from keras.layers import Input, Dense, Dropout, Conv2D, MaxPooling2D, Activation, Flatten
from keras.models import Sequential
from keras.optimizers import RMSprop
from keras.utils import np_utils
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
batch_size = 128
num_epochs = 16
hidden_size_1 = 512
hidden_size_2 = 512
height, width, depth = 28, 28, 1
num_classes = 10
(X_train, y_train), (X_test, y_test) = mnist.load_data()
num_train, width, depth = X_train.shape
num_test = X_test.shape[0]
num_classes = np.unique(y_train).shape[0]
X_save_test = np.copy(X_test)
X_train = np.expand_dims(X_train, axis=3)
X_test = np.expand_dims(X_test, axis=3)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255.
X_test /= 255.
Y_train = np_utils.to_categorical(y_train, num_classes)
Y_test = np_utils.to_categorical(y_test, num_classes)
import numpy as np
import keras as ks
model = Sequential()
model.add(Conv2D(16, (3, 3), padding='same',
input_shape=X_train.shape[1:]))
model.add(Activation('relu'))
model.add(Conv2D(64, (5, 5)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.5))
model.add(Conv2D(16, (3, 3), padding='same'))
model.add(Activation('relu'))
model.add(Conv2D(64, (5, 5)))
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.5))
model.add(Flatten())
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.5))
model.add(Dense(num_classes))
model.add(Activation('softmax'))
opt = ks.optimizers.adam(lr=0.0001, decay=0.01)
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
history = model.fit(X_train, Y_train,
batch_size=256,
epochs=32,
verbose=0)
score = model.evaluate(X_test, Y_test, verbose=1)
print 'Train accuracy:', score[1]
print 'Train loss:', score[1]
Test accuracy: 0.9939
And now we’ll do a plastic surgery on the test set and cut each letter with a 7x7 knife.
This is 25% of the width and height - we will turn the numbers into monsters and see how our network recognizes them.
XX_test = np.copy(X_save_test)
I_train = list()
I_test = list()
fig, axes = plt.subplots(1,10,figsize=(10,10))
for k in range(10):
i = np.random.choice(range(len(X_test)))
I_test.append(i)
axes[k].set_axis_off()
axes[k].imshow(X_test[i:i+1,...].reshape(28,28), cmap='gray')
st = 7
for k in xrange(X_test.shape[0]):
for i in xrange(0,X_test.shape[1],st):
for j in xrange(0,X_test.shape[2],st):
XX_test[k,i:i+st,j:j+st] = np.random.permutation( XX_test[k,i:i+st,j:j+st])
XX_test = np.expand_dims(XX_test, axis=3)
XX_test = XX_test.astype('float32')
XX_test /= 255.
fig, axes = plt.subplots(1,10,figsize=(10,10))
for k in range(10):
i = I_test[k]
axes[k].set_axis_off()
axes[k].imshow(XX_test[i:i+1,...].reshape(28,28), cmap='gray')
score = model.evaluate(XX_test, Y_test, verbose=0)
print 'Test accuracy:', score[1]
the result is pretty decent - accuracy: 0.7051. We randomly shredded each picture with a 7x7 window, despite the fact that they themselves were 28x28!
It can be seen on the slide that some of the numbers are completely crooked.
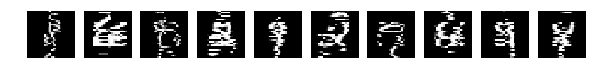
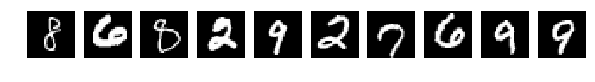
But the network copes, not very well, but copes. And if you train using different keras tricks for shifting and resizing, the result should be even better.
The conclusion is:
- in order to hide from the "big brother", shredding yourself is not necessary and useless. Save not for long.
Monsters for AI do not pose a problem, the essence will be visible to him
And now to the main topic - blondes.
Let's just recolor the numbers, because they are greyscale, just rearrange the colors in them, just like in the previous article . But let's leave the trained network as it is. Those. we train the network on the original mnist without changing anything, and repaint the test sequence.
Let me remind you that the network is trained on normal mnist and gives accuracy: 0.9939.
But we will test blondes - “colored numbers”.
I_train = list()
I_test = list()
perm = np.array(
[237, 79, 8, 182, 190, 177, 33, 121, 250, 11, 128, 48, 246, 125, 63, 92, 236, 130,
151, 93, 149, 175, 87, 234, 126, 3, 139, 217, 251, 6, 220, 70, 176, 206, 152, 228,
74, 199, 88, 24, 188, 163, 31, 211, 171, 196, 109, 64, 40, 14, 17, 119, 91, 201,
76, 27, 59, 230, 30, 57, 146, 150, 85, 214, 248, 212, 38, 104, 233, 192, 81, 120,
96, 100, 54, 95, 168, 155, 144, 205, 72, 227, 122, 60, 112, 229, 223, 242, 117, 101,
158, 55, 90, 160, 244, 203, 218, 124, 52, 254, 39, 209, 102, 216, 241, 115, 142, 166,
75, 108, 197, 181, 47, 42, 15, 133, 224, 161, 50, 68, 222, 172, 103, 174, 194, 153,
210, 7, 232, 159, 65, 238, 1, 143, 9, 207, 62, 137, 78, 110, 89, 0, 113, 243,
46, 20, 157, 184, 239, 141, 80, 200, 204, 178, 13, 99, 247, 221, 49, 16, 191, 94,
19, 169, 86, 235, 98, 131, 71, 118, 252, 129, 34, 253, 69, 18, 189, 21, 134, 22,
136, 77, 66, 225, 105, 198, 82, 245, 165, 255, 35, 183, 127, 23, 45, 116, 167, 185,
67, 73, 180, 249, 226, 154, 43, 29, 148, 83, 56, 5, 123, 140, 106, 162, 84, 44,
138, 195, 170, 53, 215, 187, 219, 132, 164, 97, 32, 156, 41, 135, 58, 173, 193, 231,
4, 107, 213, 26, 240, 25, 208, 179, 2, 36, 51, 145, 37, 202, 12, 28, 114, 147,
61, 10, 186, 111])
XX_test = np.copy(X_save_test)
fig, axes = plt.subplots(1,10,figsize=(10,10))
for k in range(10):
i = np.random.choice(range(len(X_test)))
I_test.append(i)
axes[k].set_axis_off()
axes[k].imshow(X_test[i:i+1,...].reshape(28,28), cmap='gray')
for k in xrange(X_test.shape[0]):
for i in xrange(28):
for j in xrange(28):
XX_test[k,i,j] = perm[X_save_test[k,i,j]]
fig, axes = plt.subplots(1,10,figsize=(10,10))
for k in range(10):
i = I_test[k]
axes[k].set_axis_off()
axes[k].imshow(XX_test[i:i+1,...].reshape(28,28), cmap='gray')
XX_test = np.expand_dims(XX_test, axis=3)
XX_test = XX_test.astype('float32')
XX_test /= 255.

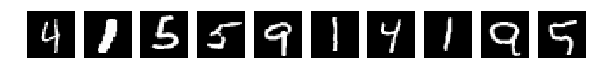
And then our super intellect suddenly showed some strange inclinations and addictions:
score = model.evaluate(XX_test, Y_test, verbose=0)
print 'Test accuracy:', score[1]
Test accuracy: 0.1634
Result accuracy: 0.1634 discourages.
Everything is clearly visible on the test slides, understandable and clear, but the result of 0.1634 suggests that the network of them all, apparently, defines it as the same number and sometimes distinguishes it.
So, to hide from Big Brother, you don't need super plastic surgeons and shreds.
All you need to do is apply makeup correctly.
PS: I apologize for associations, blondes, monsters - this is not on purpose and did not want to offend anyone. Spring, Friday - I hope they will justify me.
