Introduction

About a year ago, Oculus approached me with a proposal to sponsor my research. Essentially, they said the following: “Hi Glenn, there is a lot of interest in networked physics for VR, and you made a great talk at the GDC. Do you think you can prepare a model of network physics in VR that we could show to developers? Perhaps you can use touch controllers? ”

I answered, “Damn it!”“Ahem. Of course. It will be very interesting! ” But to be honest, I insisted on two conditions. First: the source code I developed must be published under a sufficiently free open source license (for example, BSD) so that my code will be most useful. Second: when I finish, I will have the right to write an article describing the steps that I have taken to develop this sample.

The guys from Oculus agreed. And this article! The source code for an example of network physics is available here . The code I wrote in it is released under the BSD license. I hope that the next generation of programmers will be able to learn something from my research on network physics and create something really wonderful. Good luck

What will we build?

When I first started discussing the project with Oculus, we imagined creating something like a table, at which four players can sit and interact with physically simulated cubes lying on the table. For example, throwing them, catching and building towers, maybe destroying each other's towers with a wave of hands.

But after several days of learning Unity and C #, I finally ended up inside Rift. In VR, scale is very important . When the cubes were small, everything was not particularly interesting, but when their size grew to about a meter, then there was a wonderful sense of scale. The player could create huge towers from cubes, up to 20-30 meters in height. The feeling was awesome!

It’s impossible to visually convey how everything looks in VR, but it looks something like this:


Here you can select, drag and drop cubes using the touch controller. All cubes that a player releases from their hands interact with other simulation cubes. You can throw a cube into a tower of cubes and break it. You can take a cube in each hand and juggle them. You can build towers from cubes to check how high you can get.

Although all this is very interesting, but not everything is so cloudless. Working with Oculus as a client, before starting work, I had to determine the tasks and the necessary results.

I proposed the following criteria as an assessment of success:

1. Players must be able to pick up, roll and catch dice without delay.
2. Players must be able to stack cubes in towers and these towers should become stable (come to rest) and without noticeable trembling.
3. When abandoned by any of the players interact with the simulation, such interactions should occur without delay.

At the same time, I created a set of tasks in order from the most serious to the smallest. Since this is a research paper, there was no guarantee that we will succeed in what we are trying to do.

Network models

First, we had to choose a network model. In essence, the network model is a strategy for how exactly we will hide delays and maintain simulation synchronization.

We could choose one of three main network models:

1. Determineinistic lockstep
2. Client-server with client-side prediction
3. Distributed simulation with authority scheme

I was immediately sure of the right choice of a network model: this is a distributed simulation model in which players gain authority over the cubes with which they interact. But I should share my reasoning with you.

First, I can trivially exclude the deterministic lockstep model because the Unity physics engine (PhysX) is not deterministic. Moreover, even if the PhysX was deterministic, I still could exclude this model due to the lack of necessary delays in player interaction with the simulation.

The reason for this is that in order to hide delays in the deterministic lockstep model, I would need to store two copies of the simulation and pre-predict authoritative simulation with local input before rendering (GGPO style). With a simulation frequency of 90 Hz and a delay of up to 250 ms, this meant that for each frame of visual rendering 25 physics simulation steps would be required. Costs in 25X are simply unrealistic for physical simulations with heavy CPU usage.

Therefore, there are two options left: a client-server network model with prediction on the client side (possibly with a dedicated server) and a less secure network model of distributed simulation.

Since the sample is not competitive, I found few arguments in favor of adding the costs of supporting dedicated servers. Therefore, regardless of which model of the two I implemented, the security was essentially the same. The only difference would appear only when one of the players in the game could theoretically cheat, or all players could cheat .

For this reason, the distributed simulation model was the more logical choice. In fact, it provided the same level of security, but it did not require costly rollbacks and re-simulations, since players simply get the authority to manage the cubes with which they interact and send the state of these cubes to other players.

Authorization Scheme

It is intuitively clear that obtaining permissions (to work as a server) for objects with which you interact can conceal delays - you are a server, so you have no delays, right? However, it is not entirely obvious how to resolve conflicts in this case.

What if two players interact with the same tower? If two players grab the same cube due to a delay? In the event of a conflict, who will win, whose condition is being adjusted, and how to make such decisions?

At this stage, my intuitive thoughts were as follows: since we will exchange the states of objects very quickly (up to 60 times per second), it is best to implement this as encoding in the state transmitted between the players via my network protocol, and not as events.

I thought about this for a while and came to two basic concepts:

1. Credentials
2. Possession

Each cube will have permissions, either with a default value (white color), or the colors of the player with which it interacted last. If another player interacted with the object, then the powers are changed and pass to this player. I planned to use powers for interactions of objects thrown in a scene. I imagined that the cube thrown by player 2 could take authority over all the objects with which he interacted, and those in turn would recursively with all the objects with which they interacted.

The tenure principle is slightly different. When one player owns a cube, no other player can take possession of it until the first player gives up possession. I planned to use possession for players picking cubes because I did not want players to be able to grab cubes from the hands of other players.

I had an intuitive understanding that I can represent and transfer authority and ownership as a state, adding to each cube two different consecutive numbers during its transfer: an ordinal number of powers and an ordinal number of ownership. As a result, this intuitive understanding proved its fairness, but it turned out to be much more difficult to realize than I expected. I will tell you more about this below.

State synchronization

Believing that I could implement the authorization rules described above, I decided that my first task would be to prove the possibility of synchronizing physics in one direction of the flow using Unity and PhysX. In my previous work, I created network simulations using ODE, so I really had no idea if this was possible.

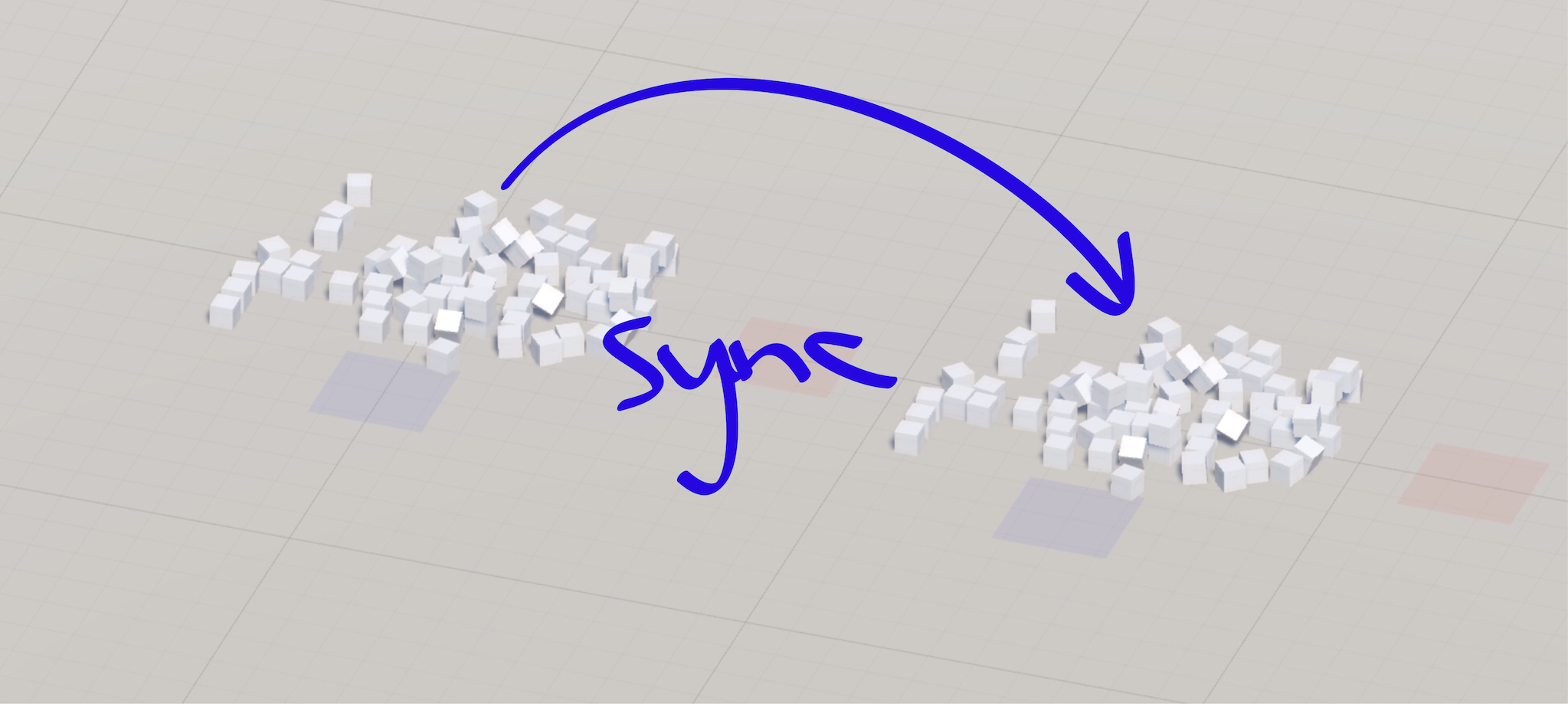
To find out, I created a loopback scene in Unity in which a bunch of cubes fell in front of the player. I had two sets of cubes. The cubes on the left represented the side of authority. The cubes on the right indicated the non-authorizing side that we wanted to synchronize with the cubes on the left.


At the very beginning, when nothing had been done to synchronize the cubes, even though both sets of cubes started from the same initial state, the final results were slightly different. This is easiest to notice in the top view:


This happened because PhysX is not deterministic. Instead of fighting non-deterministic windmills, I defeated non-determinism by getting the state from the left side (with authority) and applying it to the right side (without authority) 10 times per second:


The state obtained from each cube looks like this:

struct CubeState
{
    Vector3 position;
    Quaternion rotation;
    Vector3 linear_velocity;
    Vector3 angular_velocity;
};

And then I apply this state to the simulation on the right: I just snap the position, rotation, linear and angular velocity of each cube to the state obtained from the left side.

This simple change is enough to synchronize the left and right simulations. In 1/10 of a second, PhysX does not have enough time to deviate between updates to demonstrate any noticeable fluctuations.


This proves that the stateful synchronization approach for multiplayer can work in PhysX. (Sigh of relief) . Of course, the only problem is that transmitting an uncompressed physical state takes up too much of the channel ...

Bandwidth Optimization

To ensure the playability of a sample of network physics over the Internet, I needed to control bandwidth.

The simplest improvement method I found was simply to more efficiently encode dormant cubes. For example, instead of constantly repeating (0,0,0) for linear speed and (0,0,0) for the angular speed of cubes at rest, I send only one bit:

[position] (vector3)
[rotation] (quaternion)
[at rest] (bool)

{
    [linear_velocity] (vector3)
    [angular_velocity] (vector3)
}

This is a lossless transmission method because it does not in any way change the state transmitted over the network. In addition, it is extremely effective because statistically most of the time most cubes are at rest.

To further optimize bandwidth, we have to use lossy transmission techniques . For example, we can reduce the accuracy of the physical state transmitted over the network by limiting the position in a certain range of minima-maxima and discretizing it to a resolution of 1/1000 centimeter, then transmitting this discretized position as an integer value in a known interval. The same simple approach can be used for linear and angular velocities. I used gear to turnthe three smallest quaternion components .

But although this reduces the load on the channel, at the same time, the risk increases. I was afraid that when transmitting a tower of cubes over a network (for example, 10-20 cubes stacked on top of each other), sampling could create errors that would cause the tower to shake. Perhaps it can even lead to the instability of the tower, but in a particularly annoying and difficult to debug way, namely when the tower looks normal to you and is unstable only when viewed remotely (i.e. when simulating without authority) when another player is watching what you do.

The best solution I found to this problem was to discretize the state on both sides. This means that before each step of the simulation, I will intercept and discretize the physical state in the same way as it does when transmitting over the network, after which I apply this discretized state to the local simulation.

Then extrapolation from the discretized state on the non-authorizing side will exactly match the simulation with the authority, minimizing the trembling of tall towers. At least in theory.

Go to rest

But the discretization of the physical state created some very interesting side effects!

1. The PhysX engine doesn’t really like it when it is forced to change the state of each solid at the beginning of each frame, and it lets us know about it, consuming most of the CPU resources.
2. Discretization adds to the position an error that PhysX is stubbornly trying to eliminate, immediately and with huge leaps, removing cubes from the state of penetration into each other!
3. It is also impossible to imagine the turns accurately, which also leads to the interpenetration of cubes. Interestingly, in this case, the cubes can get stuck in the feedback loop and begin to slide on the floor!
4. Although the cubes in large towers seem to be at rest, a careful study in the editor reveals that they actually fluctuate by small values, since the cubes are discretized slightly above the surface and fall onto it.

I could do almost nothing to solve the problem with the PhysX engine consuming CPU resources, but I found a solution to get out of the interpenetration of objects. I set maxDepenetrationVelocity for each solid , limiting the speed at which cubes can repel. It turned out that a speed of one meter per second is good enough.

Bringing the cubes to rest was much more difficult. The solution I found consists in completely disabling the calculations of the rest state of the PhysX engine itself and replacing them with a ring buffer of positions and rotations for each cube. If the cube has not moved or rotated by significant values ​​during the last 16 frames, then I forcibly force it to go to rest. Boom! As a result, we got perfectly stable towerswith discretization.

This may seem like a hack, but having no way to access the PhysX source code and not being qualified to rewrite the PhysX solver and calculate the rest state, I did not see any other options. I will be happy if I turn out to be wrong, so if you can find the best solution, then please let me know

Priority accumulator

Another major bandwidth optimization was the transfer of only a subset of cubes in each packet. This gave me precise control over the amount of data transferred - I was able to set the maximum packet size and only transmit the set of updates that fit into each package.

Here's how it works in practice:

1. Each cube has a priority metric , which is calculated in each frame. The higher the value, the higher the probability of their transmission. Negative values ​​mean "this cube does not need to be transmitted . "
2. If the priority indicator is positive, then it is added to the value of the priority accumulator of each cube. This value is saved between simulation updates in such a way that the priority accumulator increases in each frame, that is, the values ​​of cubes with a higher priority grow faster than that of cubes with a low priority.
3. Negative priority metrics reset the priority accumulator to -1.0.
4. When the packet is transmitted, the cubes are sorted in order from the highest priority accumulator to the lowest. The first n cubes become a set of cubes that could potentially be included in the package. Objects with negative priority accumulator values ​​are excluded from the list.
5. The package is written and the cubes are serialized into the package in order of importance. The package does not necessarily fit all state updates, because the cube updates have an encoding of variables that depends on their current state (at rest, not at rest, and so on). Therefore, serializing packages returns a flag for each cube that determines whether it was included in the package.
6. The values ​​of the priority accumulator for cubes transferred in the package are reset to 0.0, which gives other cubes an honest chance to be included in the next package.

For this demo, I picked up the value for a significant increase in the priority of cubes recently participating in high-energy collisions, because of the non-deterministic results, high-energy collisions were one of the largest sources of deviations. I also increased the priority for cubes recently thrown by players.

It turned out to be quite counterintuitive that reducing the priority of cubes at rest leads to poor results. My theory is that since the simulation is performed on both sides, the cubes at rest can slightly out of sync and not adjust the state fast enough, which leads to deviations for other cubes that encounter them.

Delta compression

Even with all of the above methods, data transfer is still not optimized enough. For a game for four people, I wanted to make the cost per player lower than 256 kbit / s, so that for the host all the simulation could fit in the 1 Mbit / s channel.

I had the last trick up my sleeve: delta compression .

Delta compression is often used in first-person shooters: the entire state of the world is compressed relative to the previous state. In this technique, the previous full state of the world, or “snapshot,” is used as a reference point , while a set of differences, or delta , is generated and sent to the client between the reference point and the current snapshot.

This technique is (relatively) simple to implement, since the state of all objects is included in each snapshot, that is, the server just needs to track the most recent snapshot received by the client and generate a delta of differences between this snapshot and the current one.

However, when using the priority accumulator, packages do not contain updates of all objects and the delta coding process becomes more complicated. Now the server (or the party with authority) cannot just encode cubes relative to the previous snapshot number. Instead, a reference point should be specified for each cube so that the recipient knows what state each cube is encoded with.

Support systems and data structures should also become much more complex:

1. A reliability system is needed that tells the server which packets were received, and not just the number of the last snapshot received.
2. The sender must keep track of the states included in each packet being sent so that it can bind packet confirmation levels to the transmitted states and update the most recent confirmed states for each cube. The next time a cube is transmitted, its delta is encoded relative to this state as a reference point.
3. The recipient must store a ring buffer of received states for each cube so that it can recreate the current state of the cube from the delta by looking at the reference point in this ring buffer.

But in the end, the increase in complexity justifies itself, because such a system combines the flexibility and the ability to dynamically adjust the occupied bandwidth with an improvement in bandwidth by orders of magnitude due to delta coding.

Delta coding

Now that we have all the supporting structures, I need to encode the differences in the cube relative to the previous state of the anchor point. How to do this?

The simplest way to encode cubes whose state has not changed compared to the value of the reference point is just one bit: there are no changes . In addition, this is the easiest way to reduce the load on the channel, because at any time most cubes are at rest, that is, they do not change their state.

A more sophisticated strategy is coding for differencesbetween the current and the reference values, aimed at coding small changes with as few bits as possible. For example, a position delta may be (-1, + 2, + 5) relative to a reference point. I found out that this works well for linear values, but it doesn’t work well for the deltas of the three smallest quaternion components, since the largest quaternion component often differs between the anchor point and the current rotation.

In addition, although coding the differences provides us with some advantages, it does not provide improvements by orders of magnitude that I have sought. Clinging to a straw, I came up with a delta coding strategy, to which I added prediction. With this approach, I predict the current state from the reference point, assuming that the cube moves ballistically, under the influence of acceleration due to gravity.

Prediction was complicated by the fact that the prediction code had to be written with a fixed point, since floating point calculations do not guarantee determinism. But after several days of experiments, I was able to write a ballistic predictor for position, linear and angular velocity, which with discrete resolution in approximately 90% of cases corresponded to the results of the PhysX integrator.

These lucky cubes were encoded with one more bit: a perfect forecast, which led to another improvement by an order of magnitude. For cases where the forecast did not match completely, I encoded a small error offset relative to the forecast.

For all the time I spent, I could not find a good way to predict turns. I believe that the blame for this lies with the representation of the three smallest components of a quaternion, which is very unstable numerically, especially with fixed-point numbers. In the future, I will not use the representation of the three smallest components for discretized turns.

It was also painfully obvious to me that when coding differences and offsets, using a bit packer was not the best way to read and write these values. I’m sure that something like an interval encoder or an arithmetic compressor can provide much better results, which can represent fractional bits and dynamically change the model according to the differences, but at this stage I already fit into my own channel limitations and could not go for additional experiments.

Avatar synchronization

After several months of work, I made the following progress:

• Evidence that state synchronization works in Unity and PhysX
• Stable cube towers with remote viewing while sampling state on both sides
• The occupied channel is reduced to a level at which four players can fit in 1 Mbps

The next thing I needed to implement was the interaction with the simulation through touch controllers. This part was very interesting and became my favorite stage of the project.

I hope you enjoy these interactions. I had to conduct a lot of experiments and fine tuning so that such simple actions as lifting, throwing, transferring from hand to hand felt correctly. Even the crazy settings for the correct throw worked fine, while providing the ability to assemble tall towers with great accuracy.

But as for sharing over the network, in this case the game code is not important. All that is important for transmission over the network is that the avatars are presented in the form of a head and two hands, controlled by a head unit with tracking, as well as the positions and orientation of the touch controllers.

To synchronize them, I intercepted the position and orientation of the avatar components in FixedUpdate along with the rest of the physical state, and then applied this state to the avatar components in a remote viewport.

But when I tried to realize this for the first time, everything looked absolutely terrible . Why?

After debugging, I found out that the state of the avatar is sampled from the touch equipment with the frame rate of the rendering in the Update event , and is used on another machine via FixedUpdate , which leads to jitter, because the avatar’s sampling time did not correspond to the current time during remote viewing.

To solve this problem, I kept the differences between physics and rendering time when sampling the state of the avatar, and in each package included them in the state of the avatar. Then I added a jitter buffer with a delay of 100 ms to the resulting packets, which helped to eliminate the network jitter caused by time differences in packet delivery and to ensure interpolation between the avatar states to recreate the sample at the right time.

To synchronize the cubes that hold avatars when the cube is a child of the avatar’s hand, I assigned a priority indicatorcube value -1, due to which its state is not transmitted in regular updates of the physical state. When the cube is attached to the hand, I add its identifier, relative position and rotation as the state of the avatar. When viewed remotely, cubes are attached to the avatar’s hand when they receive the first state of the avatar, in which the cube becomes a child of it, and detaches from the hand when regular updates to the physical state corresponding to the moment the cube is dropped or dropped are resumed.

Bidirectional flow

Now that I created the player’s interaction with the scene using touch controllers, I began to think about how the second player can interact with the scene.

In order not to deal with the insanely constant change of two head-mounted devices, I expanded my Unity test scene and added the ability to switch between the contexts of the first (left) and second (right) players.

I called the first player "host" and the second "guest". In this model, the host is a “real” simulation, and by default synchronizes all cubes for the guest player, but when the guest interacts with the world, he receives authority over the corresponding objects and transfers their state to the host player.

In order for this to work without creating obvious conflicts, both the host and the guest must check the local state of the cubes before gaining authority and ownership. For example, a host does not take ownership of a cube that a guest already owns, and vice versa. At the same time, authorization is permitted, which allows players to roll cubes into other people's towers and break them while someone else is building.

When generalizing the system to four players in my model for implementing network physics, all packets pass through the host player, which makes it an arbiter. In fact, instead of using the true peer-to-peer topology, a topology is selected in which all guests in the game exchange data only with the host player. This allows the host to decide which of the updates to accept and which to ignore and adjust accordingly.

To apply these corrections, I needed some way to let the host take control of the guests and tell them: “No, you do not have authority / ownership of this cube, and you must accept this update.” I also needed some way so that the host could determine the order of guest interactions with the world, so that none of the clients felt an increase in delays or series of late packet delivery; these packages should not be preferable to the later activities of other guests.

As in the previous intuitive hunch, I implemented all this using two ordinal numbers for each cube:

1. The order of authority
2. Ownership Order

These ordinal numbers are transmitted with each state update, and when the cubes are held by the players, they will be included in the avatar state. They are used by the host to determine whether it should receive the update from the players, and also used by guests to determine whether the status update from the server is newer and whether it should be applied even when this guest believes that he has authority over the cube or owns them.

The ordinal number of powers increases each time a player gains powers over a cube, and when a cube whose powers belong to the player goes into a dormant state. When the guest machine has authority for the cube, the authority of this machine is preserved until it receives confirmation from the hostbefore returning to original authority. This ensures that the authority to the dormant cubes owned by the guest is ultimately transferred to the host even in the event of significant packet loss.

The ordinal number of ownership increases each time a player takes a cube. Possession is “stronger” than authority, so an increase in the ordinal number of tenure wins an increase in the ordinal number of authority. For example, if a player interacts with the cube just before another player takes it, then the player who takes the cube wins.

Based on my experience with this demo, I found out that these rules are enough to resolve conflicts, at the same time they provide interaction with the host and guest world without delay. In practice, conflicts that need to be corrected are rare even in the event of a significant delay, and when they arise, the simulation quickly leads them to a consistent state.

Conclusion

High-quality network physics with stable cubic towers can be best used only for cooperative gameplay , since it does not provide security at the level of the network model of an authoritative server with dedicated servers and client-side forecasting. I thank Oculus for sponsoring my work and the opportunity to conduct this research! The source code for a sample of network physics can be downloaded here .