Volumetric atmospheric light scattering
- Transfer

If you have lived on planet Earth long enough, you probably wondered why the sky is usually blue, but blushes at sunset. The optical phenomenon that has become the (main) reason for this is called Rayleigh scattering . In this article, I will describe how to simulate atmospheric scattering in order to simulate many of the visual effects that appear on planets. If you want to learn how to render physically accurate images of alien planets, then this tutorial is definitely worth exploring.
GIF

The article is divided into the following parts:
- Part 1. Volumetric atmospheric scattering
- Part 2. Theory of atmospheric scattering
- Part 3. Mathematics of Rayleigh scattering
- Part 4. Traveling through the atmosphere
- Part 5. Atmospheric Shader
- Part 6. Intersection of the atmosphere
- Part 7. Atmospheric dispersion shader
Part 1. Volumetric atmospheric scattering
Introduction
It is so difficult to recreate atmospheric phenomena because the sky is not an opaque object. Traditional rendering techniques assume that objects are just empty shells. All graphic calculations are performed on the surfaces of materials and do not depend on what is inside. This powerful simplification allows the rendering of opaque objects very efficiently. However, the properties of some materials are determined by the fact that light can pass through them. The final appearance of translucent objects is the result of the interaction of light with their internal structure. In most cases, this interaction can be very effectively simulated, as can be seen in the tutorial " Fast Shader for Subsurface Scattering in Unity". Unfortunately, in our case, if we want to create a convincing sky, this is not so. Instead of rendering only the" outer shell "of the planet, we have to simulate what happens to the rays of light passing through the atmosphere. Performing calculations inside an object is called volume rendering ; this subject we discussed in detail in a series of articles Volumetric Rendering in this article series, I talked about the two techniques (. raymarching and iconic function of the distance ), which can not be effectively used for the simulation of atmospheric dispersion in this article. we will look at more suitable for rendering translucent objects solid technique, often referred to as a single volumetric scattering .
Single scattering
In a room without light, we will not see anything. Objects become visible only when light rays are reflected from them and enter our eye. Most game engines (such as Unity and Unreal) assume that light moves in a "vacuum." This means that only objects can influence light. In fact, light always moves in the environment. In our case, such a medium is the air we inhale. Therefore, the distance traveled by light in air affects the appearance of an object. On the surface of the Earth, the density of air is relatively small, its influence is so insignificant that it should be taken into account only when light travels long distances. Distant mountains merge with the sky, but atmospheric dispersion has almost no effect on nearby objects.
The first step in recreating the optical effect of atmospheric scattering is to analyze how light passes through media such as air. As stated above, we can only see an object when light falls into our eyes. In the context of 3D graphics, our eye is the camera used to render the scene. The molecules that make up the air around us can reflect light rays passing through them. Therefore, they are able to change the way we perceive objects. If greatly simplified, there are two ways that molecules can affect our eyesight.
Outward scattering
The most obvious way molecules interact with light is that they reflect light, changing its direction. If a ray of light directed into the camera is reflected, then we observe a process of scattering outward .

A real light source can emit quadrillion photons every second, and each of them with a certain probability can collide with an air molecule. The denser the medium in which the light moves, the more likely is the reflection of a single photon. The effect of outward scattering also depends on the distance traveled by the light.

Outward scattering leads to the fact that the light gradually becomes more and more dim, and this property depends on the distance traveled and the density of air.
Scattering inward
When light is reflected by a particle, it may happen that it is redirected to the camera. Such an effect is the opposite of outward scattering, and it is logical that it is called inward scattering .
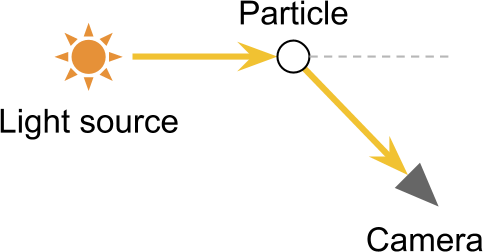
Under certain conditions, scattering inward allows you to see light sources that are not in the direct field of view of the camera. The most obvious result of this is the optical effect - light halo around light sources. They arise due to the fact that the camera receives from one source both direct and indirect rays of light, which de facto increases the number of photons received.
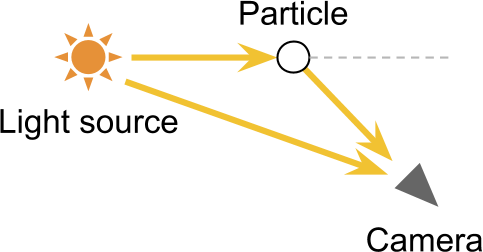
Unit Volumetric Scattering
One ray of light can be reflected an arbitrary number of times. This means that before you get into the camera. the beam can travel very difficult routes. This becomes a serious difficulty for us, because rendering high-quality translucent materials requires simulating the paths of each of the individual rays of light. This technique is called raytracing , and is currently too costly to implement in real time. The unit scattering technique presented in this tutorial takes into account a single light ray scattering event. Later we will see that such a simplification still allows you to get realistic results in just a small fraction of the calculations necessary for real ray tracing.
The basis of rendering a realistic sky is to simulate what happens to the rays of light when passing through the atmosphere of a planet. The diagram below shows a camera looking through a planet. The main idea of this rendering technique is to calculate how light travels from
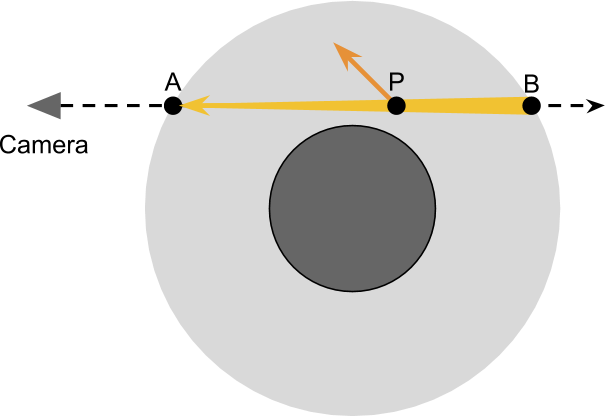
To correctly take into account the amount of outward scattering occurring at each point
These two steps are enough to approximate most of the effects observed in the atmosphere. However, everything is complicated by the fact that the amount of light received

To summarize what we need to do:
- The scope of the camera enters the atmosphere in
and is located in
;
- As an approximation, we will take into account the effect of scattering in and out when it occurs at each point
;
- The amount of light received
from the sun;
- The amount of light received
and subject to scattering outward when passing through the atmosphere
;
- Part of the Light Received
and prone to scattering inward, which redirects the rays into the chamber;
- Part of the world from
directed into the chamber is scattered outward and reflected from the field of view.
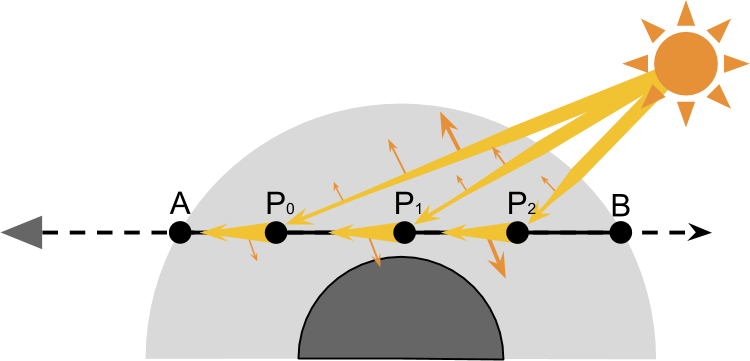
This is not the only way that rays of light can enter the camera!
The solution proposed in this tutorial takes into account scattering inward along the scope  . Light reaching the point
. Light reaching the point from the sun, with a certain probability can be reflected in the camera.
from the sun, with a certain probability can be reflected in the camera.
However, there are many ways in which rays can enter the camera. For example, one of the rays scattered outward on the way to , in a second collision, it can scatter back towards the camera (see diagram below). And there may be rays reaching the camera after three reflections, or even four.
, in a second collision, it can scatter back towards the camera (see diagram below). And there may be rays reaching the camera after three reflections, or even four.

The technique we are considering is called single scattering , because it takes into account only scattering inward along the field of view. More sophisticated techniques can expand this process and take into account other ways in which the beam can reach the camera. However, the number of possible paths grows with an increase in the number of scattering events considered exponentially. Fortunately, the likelihood of getting into the camera also decreases exponentially.
However, there are many ways in which rays can enter the camera. For example, one of the rays scattered outward on the way to

The technique we are considering is called single scattering , because it takes into account only scattering inward along the field of view. More sophisticated techniques can expand this process and take into account other ways in which the beam can reach the camera. However, the number of possible paths grows with an increase in the number of scattering events considered exponentially. Fortunately, the likelihood of getting into the camera also decreases exponentially.
Part 2. Theory of atmospheric scattering
In this part, we will begin to derive the equations governing this complex but wonderful optical phenomenon.
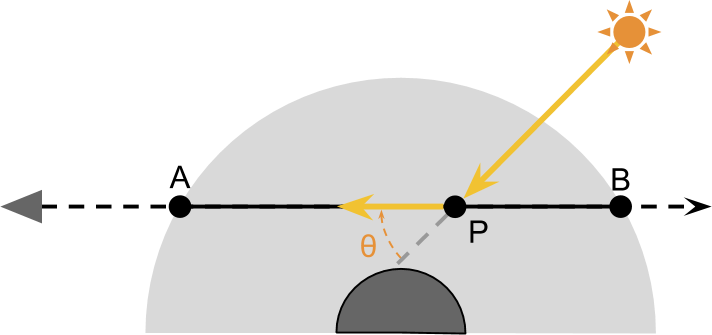
Transmission function
To calculate the amount of light transmitted to the camera, it is useful to take the same journey that the rays from the sun pass. Looking at the diagram below, it is easy to see that the rays of light reaching

Ratio
We can use it to indicate the percentage of light that was not scattered (i.e. was missed ) when traveling from
Consequently, the amount of light received
Scatter function
Point

Value
Now we have all the necessary tools for writing a general equation showing the amount of light transmitted from
Thanks to the previous definition, we can expand
The equation speaks for itself:
- Light travels from the sun to
without scattering in the vacuum of space;
- Light enters the atmosphere and passes from
to
. In this process, due to the scattering outward only part
reaches the destination;
- Part of the light that got from the sun to
reflected back to the camera. The fraction of light subject to inward scattering is
;
- The remaining light passes from
before
, and again only part
.
Numerical integration
If you carefully read the previous paragraphs, you might notice that the brightness was recorded in different ways. Symbol
The total amount of light received
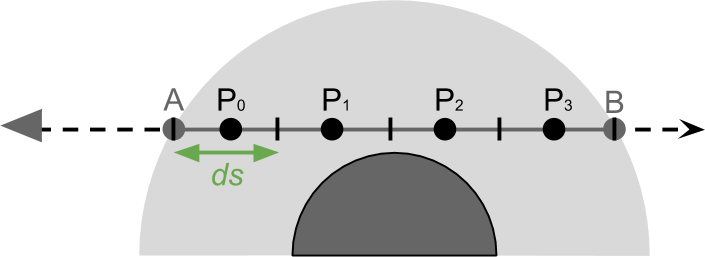
Such an approximation process is called numerical integration and leads to the following expression:
The more points we take into account, the more accurate the final result will be. In reality, in our atmospheric shader, we simply cycle around several points
Why do we multiply by ds?
Here we use the approximation of a continuous phenomenon. The more points we consider, the closer we will be to the real result. Multiplying each point by , we give its influence weight according to its length. The more points we have, the less important each of them is.
, we give its influence weight according to its length. The more points we have, the less important each of them is.
You can look at it differently: multiplying by , we “average” the influence of all points.
, we “average” the influence of all points.
You can look at it differently: multiplying by
Directional lighting
If the sun is relatively close, then it is best to model it as a point source of light . In this case, the amount received
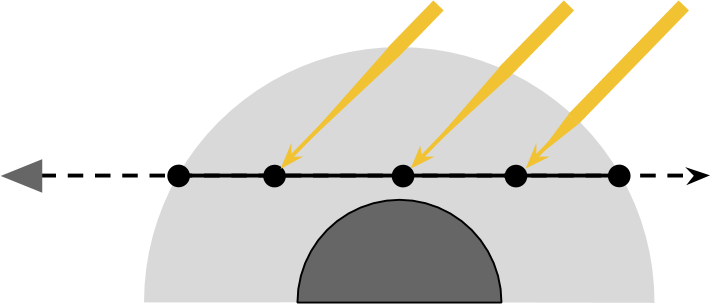
We can use this assumption to simplify our equations.
Let's replace
There is another optimization we can perform, it includes a scatter function
Absorption coefficient
In describing the possible results of the interaction between light and air molecules, we allowed only two options - either through and through, or reflection. But there is a third possibility. Some chemical compounds absorb light. There are many substances in the Earth’s atmosphere that have this property. Ozone, for example, is in the upper atmosphere and actively interacts with ultraviolet radiation. However, its presence has practically no effect on the color of the sky, because it absorbs light outside the visible spectrum. Here on Earth, the effects of light-absorbing substances are often ignored. But in the case of other planets it is impossible to refuse it. For example, the usual coloration of Neptune and Uranus is caused by the presence of a large amount of methane in their atmosphere. Methane absorbs red light, which gives a blue tint.
Почему Солнце стало красным во время урагана Офелия 2017 года?
Если вы живёте в Великобритании, то могли заметить, что во время урагана Офелия солнце становилось красным. Так происходило потому, что Офелия принесла песок из Сахары. Эти крошечные частицы, висевшие в воздухе, усиливали эффект рассеяния. Как мы увидим в следующей части, синий свет рассеивается сильнее, чем красный.
Если посмотреть на цвета видимого спектра (ниже), то легко увидеть, что если рассеивается достаточное количество синего света, то небо и в самом деле может стать жёлтым или красным.

Есть искушение сказать, что цвет окраски неба связан с оттенком жёлтого сахарского песка. Однако такой же эффект можно увидеть во время больших пожаров из-за частиц дыма, которые обычно близки к чёрному цвету.
Если посмотреть на цвета видимого спектра (ниже), то легко увидеть, что если рассеивается достаточное количество синего света, то небо и в самом деле может стать жёлтым или красным.

Есть искушение сказать, что цвет окраски неба связан с оттенком жёлтого сахарского песка. Однако такой же эффект можно увидеть во время больших пожаров из-за частиц дыма, которые обычно близки к чёрному цвету.
Часть 3. Математика рэлеевского рассеяния.
In this part, we will get acquainted with the mathematics of Rayleigh scattering - an optical phenomenon due to which the sky looks blue. The equations derived in this part of the equation will be transferred to the shader code of the next part.
Introduction
In the previous part, we derived an equation that provides a good basis for approximating atmospheric scattering in a shader. However, we have missed the fact that one equation will not give us convincing results. If we need a beautiful looking atmospheric shader, then we need to go a little deeper into mathematics.
The interaction between light and matter is incredibly complex, and we will not be able to fully describe it in an easy way. Actually, modeling atmospheric scattering is very time consuming. Part of the problem is that the atmosphere is not a homogeneous environment. Its density and composition vary significantly as a function of height, which makes it almost impossible to create an “ideal” model.
That is why several scattering models are given in the scientific literature, each of which is intended to describe a subset of the optical phenomena that arise under certain conditions. Most of the optical effects demonstrated by the planets can be recreated, taking into account only two different models: Rayleigh scattering and scattering of light by a spherical particle . These two mathematical tools make it possible to predict light scattering on objects of various sizes. The first models the reflection of light by oxygen and nitrogen molecules, which make up most of the air. The latter models the reflection of light in larger structures present in the lower atmosphere, such as pollen, dust and pollutants.
Rayleigh scattering is the cause of blue sky and red sunsets. Scattering of light by a spherical particle gives the clouds their white color. If you want to know how this happens, then we will have to dive deeper into the mathematics of scattering.
Rayleigh scattering
What is the fate of a photon striking a particle? To answer this question, we need to rephrase it more formally. Imagine that a ray of light passes through an empty space and suddenly collides with a particle. The result of such a collision is highly dependent on the particle size and color of the light beam. If the particle is small enough (the size of atoms or molecules), then the behavior of light is better predicted using Rayleigh scattering .
What is going on? Part of the world continues its journey, “not feeling” any influence. However, a small percentage of this source light interacts with the particle and scatters in all directions. However, not all directions receive the same amount of light. Photons are more likely to pass directly through the particle or bounce back. That is, the photon reflection option is 90 degrees less large. This behavior can be seen in the diagram below. The blue line shows the most likely directions of the scattered light.

This optical phenomenon is mathematically described by the Rayleigh scattering equation
Where:
: wavelength of the incoming light;
: Angle rasseiyaniya (scattering angle) ;
: высота (altitude) точки;
: коэффициент преломления воздуха;
: количество молекул на кубический метр стандартной атмосферы;
: коэффициент плотности.Это число на уровне моря равно
, и экспоненциально уменьшается с увеличением
. Об этой функции можно многое сказать, и мы рассмотрим её в следующих частях.
Но это не уравнение рэлеевского рассеяния!
Если вы встречались с рэлеевским рассеянием не в области компьютерной графики, то есть вероятность, что вы видели другое уравнение. Например, представленное в статье «Рэлеевское рассеяни» на Википедии, сильное отличается.
Использованное в этом туториале уравнение взято из научной статьи Display of The Earth Taking into Account Atmospheric Scattering, Нишиты et al.
Использованное в этом туториале уравнение взято из научной статьи Display of The Earth Taking into Account Atmospheric Scattering, Нишиты et al.
Откуда взялась эта функция?
Одна из задач этого блога — объяснение вывода всех получаемых величин. К сожалению, это не относится к рэлеевскому рассеянию.
Если вам всё-таки интересно разобраться, почему частицы света так странно отражаются от молекул воздуха, то интуитивное понимание происходящего может дать следующее объяснение.
Причиной рэлеевского рассеяния на самом деле является не «отталкивание» частиц. Свет — это электромагнитная волна, и она может взаимодействовать с неравновесием зарядов, присутствующим в определённых молекулах. Эти заряды насыщаются поглощением получаемого электромагнитного излучения, которое позже испускается снова. Показанная в угловой функции двудольная форма показывает, как молекулы воздуха становятся электрическими диполями, излучающими подобно микроскопическим антеннам.
Если вам всё-таки интересно разобраться, почему частицы света так странно отражаются от молекул воздуха, то интуитивное понимание происходящего может дать следующее объяснение.
Причиной рэлеевского рассеяния на самом деле является не «отталкивание» частиц. Свет — это электромагнитная волна, и она может взаимодействовать с неравновесием зарядов, присутствующим в определённых молекулах. Эти заряды насыщаются поглощением получаемого электромагнитного излучения, которое позже испускается снова. Показанная в угловой функции двудольная форма показывает, как молекулы воздуха становятся электрическими диполями, излучающими подобно микроскопическим антеннам.
The first thing that can be seen in Rayleigh scattering is that in some directions more light travels than in others. The second important aspect is that the amount of scattered light is highly dependent on the wavelength.

The figure below shows the visualization of the scattering coefficients for the continuous wavelength / color range of the visible spectrum (the code is available in ShaderToy ).
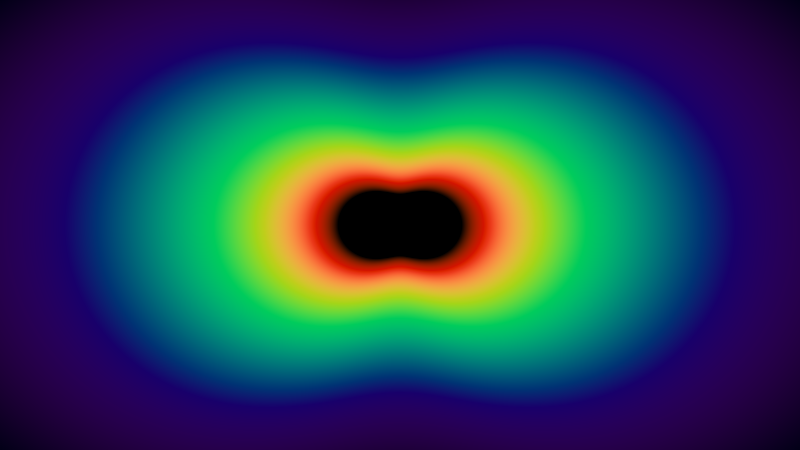
The center of the image appears black because the wavelengths in this range are outside the visible spectrum.
Rayleigh scattering coefficient
The Rayleigh scattering equation shows how much light is scattered in a certain direction. However, it does not tell us how much energy has been dissipated. To calculate this, we need to take into account energy dissipation in all directions. The derivation of the equation is not easy; if you haven’t mastered complex matanalysis, here is the result:
Where
If you read the previous part of the tutorial, you can guess that
Unfortunately, the calculation
Show me the calculations!
The Rayleigh scattering equation shows us the fraction of the energy scattered in a certain direction. To calculate the total loss, we need to consider all possible directions. For summation over a continuous interval, integration is required .
You can try to integrate by
by  on the interval
on the interval ![$\left[0,2\pi\right]$](https://habrastorage.org/getpro/habr/formulas/825/edc/9d5/825edc9d5aed9473c5a61ad4da768f91.svg) , но это будет ошибкой.
, но это будет ошибкой.
Несмотря на то, что мы визуализировали рэлеевское рассеяние в двух измерениях, на самом деле это трёхмерное явление. Угол рассеяния может принимать любое направление в 3D-пространстве. Вычисления с учётом полного распределения функции, которое зависит от
может принимать любое направление в 3D-пространстве. Вычисления с учётом полного распределения функции, которое зависит от  в трёхмерном пространстве (как
в трёхмерном пространстве (как  ) называется интегрированием по телесному углу:
) называется интегрированием по телесному углу:
Внутренний интеграл перемещает в плоскости XY, а внешний — поворачивает результат вокруг оси X, чтобы учесть третье измерение. Прибавляемый
в плоскости XY, а внешний — поворачивает результат вокруг оси X, чтобы учесть третье измерение. Прибавляемый  используется для сферических углов.
используется для сферических углов.
Процесс интегрирования интересует только то, что зависит от . Несколько членов
. Несколько членов  постоянны, поэтому их можно перенести из под знака интеграла:
постоянны, поэтому их можно перенести из под знака интеграла:
Это значительно упрощает внутренний интеграл, который теперь принимает следующий вид:
Now we can perform external integration:
Which brings us to the final form:
Since this is an integral that takes into account the effect of scattering in all directions, it is logical that the expression no longer depends on .
.
You can try to integrate
Несмотря на то, что мы визуализировали рэлеевское рассеяние в двух измерениях, на самом деле это трёхмерное явление. Угол рассеяния
Внутренний интеграл перемещает
Процесс интегрирования интересует только то, что зависит от
Это значительно упрощает внутренний интеграл, который теперь принимает следующий вид:
Now we can perform external integration:
Which brings us to the final form:
Since this is an integral that takes into account the effect of scattering in all directions, it is logical that the expression no longer depends on
This new equation gives us another way to understand how different colors are scattered. The graph below shows the amount of scattering to which light is exposed, as a function of its wavelength.

This is a strong relationship between the scattering coefficient.
Reasoning the same way, we can understand why the sky looks blue. The light of the sun is falling from one direction. However, its blue component is scattered in all directions. When we look at the sky, blue light comes from all directions.
Rayleigh phase function
The original equation describing Rayleigh scattering,
This new value
You can see that this new expression is independent of the wavelength of the incoming light. This seems counterintuitive because we know for sure that Rayleigh scattering affects shortwaves more strongly.
However
In the following parts, we will see how the separation of these two components allows us to derive more efficient equations.
To summarize
- Rayleigh scattering equation : indicates the fraction of light reflected in the direction
. The amount of scattering depends on the wavelength.
incoming light.
Moreover:
- Rayleigh scattering coefficient : indicates the fraction of light lost due to scattering after the first collision.
- Rayleigh scattering coefficient at sea level : this is an analog
. Creating this additional coefficient will be very useful for deriving more efficient equations.
If we consider wavelengths roughly corresponding to the red, green, and blue colors, we will obtain the following results:
These results are calculated under the assumption that
- Rayleigh phase function : controls the scattering geometry, which denotes the relative fraction of light lost in a particular direction. Coefficient
serves as a normalization coefficient, therefore, the integral over the unit sphere will be
.
- Density coefficient : This function is used to simulate the density of the atmosphere. Its formal definition will be presented below. If you are not against mathematical spoilers, then it is defined as follows:
Where
Part 4. Travel through the atmosphere.
In this part, we will consider modeling atmospheric density at different heights. This is a necessary step, because the density of the atmosphere is one of the parameters necessary for the correct calculation of Rayleigh scattering.
Atmospheric density coefficient
So far, we have not considered the role of the atmospheric density coefficient
The diagram below shows the relationship between density and height in the lower atmosphere.
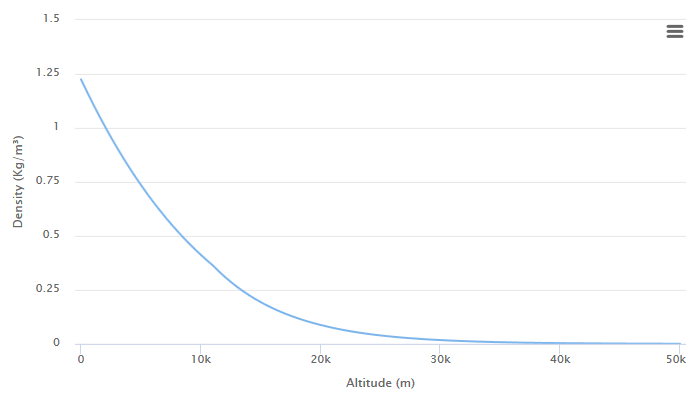
Value
Dividing the true density by
If we want to approximate the density coefficient through an exponential curve, then we can do this as follows:
Where
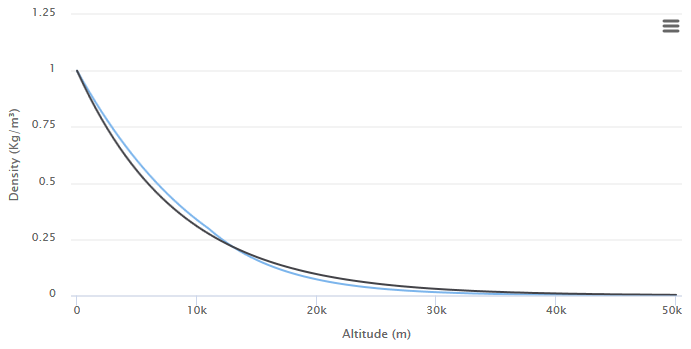
The value used for
Exponential decrease
In the previous part of the tutorial, we derived an equation showing us how to account for the outward scattering to which a ray of light is exposed after interacting with an individual particle. The value used to model this phenomenon was called the scattering coefficient
In the case of Rayleigh scattering, we also derived a closed form for calculating the amount of light subject to atmospheric scattering in a single interaction:
When calculating at sea level, i.e. when
Where
What is the meaning of these numbers? They represent the fraction of light that is lost in a single interaction with a particle. Assuming that a ray of light initially has brightness
This is true for a single collision, but we are interested in what kind of energy is dissipated during a certain distance. This means that the remaining light undergoes this process at every point.
When light passes through a homogeneous medium with a scattering coefficient
For those of you who have studied matanalysis, this may seem familiar. When a multiplicative process is repeated on a continuous segment
And again, we are faced with an exponential function. It has nothing to do with the exponential function describing the density coefficient
Where did exp come from?
If you are unfamiliar with matanalysis, you may not understand why such a simple process as  converted to
converted to  .
.
We can consider the original expression as the first approximation to the solution. If we want to get a closer approximation, then we need to take into account two scattering events, halving the scattering coefficient for each of them:
Which leads us to the following:
This is a new expression for shows the amount of energy saved after two collisions. What about the three collisions? Or four? Or five? In general terms, this can be written as follows:
shows the amount of energy saved after two collisions. What about the three collisions? Or four? Or five? In general terms, this can be written as follows:
Where - This is a mathematical construction that allows you to repeat the process an infinite number of times. We need this because
- This is a mathematical construction that allows you to repeat the process an infinite number of times. We need this because technically is not a chill, as in this context it does not make sense to write something like
technically is not a chill, as in this context it does not make sense to write something like  .
.
This expression is the very definition of an exponential function:
which describes the amount of energy stored after the multiplicative process on a continuous interval.
We can consider the original expression as the first approximation to the solution. If we want to get a closer approximation, then we need to take into account two scattering events, halving the scattering coefficient for each of them:
Which leads us to the following:
This is a new expression for
Where
This expression is the very definition of an exponential function:
which describes the amount of energy stored after the multiplicative process on a continuous interval.
Uniform transmittance
In the second part of the tutorial we introduced the concept of transmission
Let's look at the diagram below and think about how to calculate the transmittance for the segment

The amount of scattered light depends on the distance traveled. The longer the path, the greater the attenuation. According to the law of exponential reduction, the amount of light at a point
Where
Atmospheric transmission
We based our equation on the assumption that the probability of reflection ( scattering coefficient
The scattering coefficient is highly dependent on the density of the atmosphere. The more air molecules per cubic meter, the higher the chance of a collision. The density of the planet’s atmosphere is heterogeneous, and varies with altitude. It also means that we cannot calculate outward scatterings from
To understand how this works, let's start with the approximation. Section

First we calculate the amount of light from
Then we use the same approach to calculate the amount of light reaching
If we substitute

If
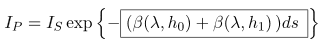
In the case of two segments of the same length with different scattering coefficients, the outward scattering is calculated by summing the scattering coefficients of the individual segments and multiplied by the lengths of the segments.
We can repeat this process with an arbitrary number of segments, getting closer and closer to the true value. This will lead us to the following equation:
Where
The method of dividing a straight line into many segments, which we just used, is called numerical integration .
If we assume that the initial amount of light received is
We can expand this expression even further. replacing the total
Many factors
The value expressed by summation is called the optical thickness
Summarize:
Part 5. Atmospheric shader.
Introduction
Writing shader
We can start writing a shader for this effect in an infinite number of ways. Since we want to render atmospheric scattering on planets, it is logical to assume that it will be used on spheres.
If you use this tutorial to create a game, chances are that you will apply a shader to an existing planet. Adding atmospheric scatter calculations on top of the swatch is possible, but usually produces poor results. The reason is that the atmosphere is larger than the radius of the planet, so it needs to be rendered on a transparent sphere of a slightly larger size. The figure below shows how the atmosphere extends over the surface of the planet, mixing with the empty space behind it.

The application of dispersible material to a separate sphere is possible, but redundant. In this tutorial, I suggest expanding Standard Surface Shader Unity by adding a shader pass that renders the atmosphere in a slightly larger sphere. We will call it the atmospheric sphere .
Two-pass shader
If you used to work with Unity surface shaders , you may have noticed that they do not support a block
Pass, with which several passes are set in the vertex and fragment shaders . Creating a shader with two passes is possible, just add two separate sections of the CG code in one block
SubShader:Shader "Custom/NewSurfaceShader" {
Properties {
_Color ("Color", Color) = (1,1,1,1)
_MainTex ("Albedo (RGB)", 2D) = "white" {}
_Glossiness ("Smoothness", Range(0,1)) = 0.5
_Metallic ("Metallic", Range(0,1)) = 0.0
}
SubShader {
// --- Первый проход ---
Tags { "RenderType"="Opaque" }
LOD 200
CGPROGRAM
// Здесь код Cg
ENDCG
// ------------------
// --- Второй проход ---
Tags { "RenderType"="Opaque" }
LOD 200
CGPROGRAM
// Здесь код Cg
ENDCG
// -------------------
}
FallBack "Diffuse"
}You can change the first pass to render the planet. From now on, we will focus on the second pass, realizing atmospheric scattering in it.
Normal Extrusion
The atmospheric sphere is slightly larger than the planet. This means that the second pass should extrude the sphere out. If your model uses smooth normals, then we can achieve this effect using a technique called extrusion of normals .
Normal extrusion is one of the oldest shader tricks, and is usually one of the first to be studied. My blog has many references to it; A good start might be a Surface Shader post from the A Gentle Introduction to Shaders series .
If you are unfamiliar with how the extrusion of normals works, then I will explain: all the vertices are processed by the shader using its vertex function. We can use this function to change the position of each vertex, making the sphere bigger.
The first step is to change the directive by
pragmaadding it vertex:vert; this will force Unity to execute a function for each vertex vert.#pragma surface surf StandardScattering vertex:vert
void vert (inout appdata_full v, out Input o)
{
UNITY_INITIALIZE_OUTPUT(Input,o);
v.vertex.xyz += v.normal * (_AtmosphereRadius - _PlanetRadius);
}This code fragment shows a vertex function extruding a sphere along its normals. The magnitude of the extrusion of a sphere depends on the size of the atmosphere and the size of the planet. Both of these values need to be passed to the shader as properties that can be accessed through the material inspector .
Our shader also needs to know where the center of the planet is. We can add its calculation to the vertex function too. We discussed the finding of the center point of an object in the space of the world in the article Vertex and Fragment Shaders .
struct Input
{
float2 uv_MainTex;
float3 worldPos; // Автоматически инициализируется Unity
float3 centre; // Инициализируется в вершинной функции
};
void vert (inout appdata_full v, out Input o)
{
UNITY_INITIALIZE_OUTPUT(Input,o);
v.vertex.xyz += v.normal * (_AtmosphereRadius - _PlanetRadius);
o.centre = mul(unity_ObjectToWorld, half4(0,0,0,1));
}What is UNITY_INITIALIZE_OUTPUT?
Если посмотреть на вершинную функцию, то можно заметить, что она всегда содержит таинственный вызов
И это одна из операций, выполняемых
UNITY_INITIALIZE_OUTPUT. Шейдер получает позицию вершин в пространстве объекта, и ему нужно спроецировать их в координаты мира с помощью предоставляемых Unity положения, масштаба и поворота.И это одна из операций, выполняемых
UNITY_INITIALIZE_OUTPUT. Без него нам бы пришлось писать необходимый для этих вычислений код самостоятельно.Аддитивное смешивание
Another interesting feature that we need to deal with is transparency. Usually transparent material allows you to see what is behind the object. This solution in our case will not work, because the atmosphere is not just a transparent piece of plastic. Light passes through it, so we need to use the additive mixing mode to increase the luminosity of the planet.
In the standard Unity Surface Shader, no blending mode is enabled by default. To change the situation, we will have to replace the labels in the second pass with the following:
Tags { "RenderType"="Transparent"
"Queue"="Transparent"}
LOD 200
Cull Back
Blend One OneThe expression is
Blend One Oneused by the shader to access the additive blending mode.Native lighting function
Most often, when writing a surface shader, programmers change its function
surf, which is used to provide “physical” properties, such as albedo, surface smoothness, metal properties, etc. All these properties are then used by the shader to calculate realistic shading. In our case, these calculations are not required. To get rid of them, we need to remove the lighting model used by the shader . I examined this topic in detail; You can study the following posts to figure out how to do this:
- 3D Printer Shader Effect ( translation on Habré)
- CD-ROM Shader: Diffraction Grating
- Fast Subsurface Scattering in Unity ( Habré translation )
The new lighting model will be called
StandardScattering; we must create a function for lighting in real time and for global illumination, that is, respectively, LightingStandardScatteringand LightingStandardScattering_GI. The code that we need to write will also use properties such as the direction of lighting and the direction of view . They can be obtained using the following code snippet.
#pragma surface surf StandardScattering vertex:vert
#include "UnityPBSLighting.cginc"
inline fixed4 LightingStandardScattering(SurfaceOutputStandard s, fixed3 viewDir, UnityGI gi)
{
float3 L = gi.light.dir;
float3 V = viewDir;
float3 N = s.Normal;
float3 S = L; // Направление освещения от солнца
float3 D = -V; // Направление луча видимости, проходящего через атмосферу
...
}
void LightingStandardScattering_GI(SurfaceOutputStandard s, UnityGIInput data, inout UnityGI gi)
{
LightingStandard_GI(s, data, gi);
}It
...will contain the shader code itself, which is needed to implement this effect.Floating point precision
In this tutorial we will assume that all calculations are performed in meters. This means that if we need to simulate the Earth, then we need a sphere with a radius of 6371000 meters. In fact, in Unity this is not possible due to floating point errors that occur when you have to work with very large and very small numbers at the same time.
To circumvent these limitations, you can scale the scattering coefficient to compensate. For example, if the planet has a radius of only 6.371 meters, then the scattering coefficient
In my Unity project, all properties and calculations are expressed in meters. This allows us to use real, physical values for the scattering coefficients and the reduced height. However, the shader also gets the size of the sphere in meters, so that it can perform scale conversion from Unity units to real-scale meters.
Part 6. Intersection of the atmosphere.
As mentioned above, the only way to calculate the optical thickness of a segment passing through the atmosphere is through numerical integration . This means that you need to divide the interval into smaller lengths

Above is the optical thickness.
The first step will obviously be finding the points
worldPosin the structure Input. This is the amount of work the shader does; the only information available to us is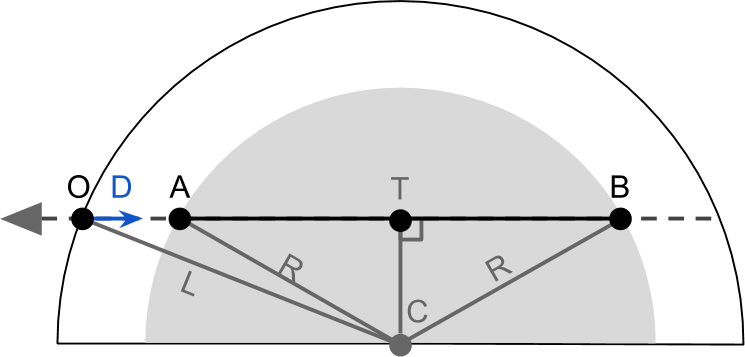
Firstly, it is worth noting that
float3), andfloat).where is the entry with a bar above
In the shader code for efficiency we will use
It is also worth noting that the segments
Section
It is also worth noting that
Next we need to calculate the length of the segment
And that means that:
Length
Now we have all the necessary quantities. Summarize:
There are square roots in this set of equations. They are defined only for non-negative numbers. If
We can convert this to the following Cg function:
bool rayIntersect
(
// Ray
float3 O, // Origin
float3 D, // Направление
// Сфера
float3 C, // Центр
float R, // Радиус
out float AO, // Время первого пересечения
out float BO // Время второго пересечения
)
{
float3 L = C - O;
float DT = dot (L, D);
float R2 = R * R;
float CT2 = dot(L,L) - DT*DT;
// Точка пересечения за пределами круга
if (CT2 > R2)
return false;
float AT = sqrt(R2 - CT2);
float BT = AT;
AO = DT - AT;
BO = DT + BT;
return true;
}It returns not one, but three values
outthat save after the function completes any changes that it made to these parameters.Collision with the planet
There is another problem to consider. Some rays of visibility collide with the planet, so their journey through the atmosphere ends early. One solution is to revise the above.
A simpler but less effective approach is to perform
rayIntersecttwice and change the endpoint if necessary.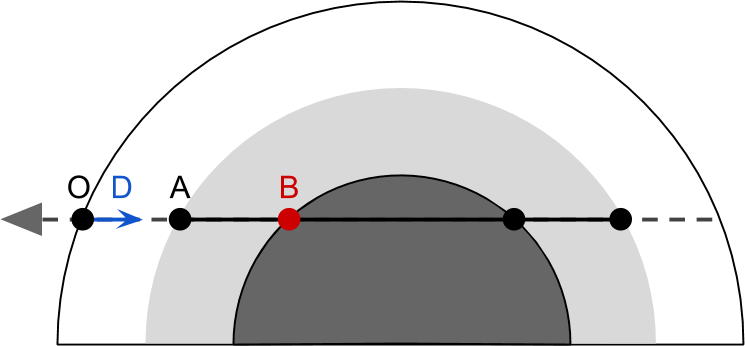
This translates to the following code:
// Пересечения с атмосферной сферой
float tA; // Точка входа в атмосферу (worldPos + V * tA)
float tB; // Точка выхода из атмосферы (worldPos + V * tB)
if (!rayIntersect(O, D, _PlanetCentre, _AtmosphereRadius, tA, tB))
return fixed4(0,0,0,0); // Лучи видимости смотрят в глубокий космос
// Проходит ли луч через ядро планеты?
float pA, pB;
if (rayIntersect(O, D, _PlanetCentre, _PlanetRadius, pA, pB))
tB = pA;Part 7. Atmospheric dispersion shader.
In this part, we will finally complete the work on simulating Rayleigh scattering in the atmosphere of the planet.
GIF

Visibility Beam Sampling
Let's recall the equation of atmospheric scattering that we recently derived:
The amount of light we receive is equal to the amount of light emitted by the sun,
We can implement this function directly in the shader. However, some optimizations need to be made here. In the previous part, I said that the expression can be simplified even more. The first thing to do is to break up the scattering function into two main components:
Phase function
This new expression is mathematically similar to the previous one, but more efficient in calculating, because the most "heavy" parts are derived from the sum.
We are not yet ready for its implementation. There are an infinite number of points

The number of segments in
_ViewSamples. Since this property, we can access it from the material inspector. This allows us to reduce the accuracy of the shader for its performance. The following code snippet allows you to bypass all segments in the atmosphere.
// Численное интегрирование для вычисления
// влияния света в каждой точке P отрезка AB
float3 totalViewSamples = 0;
float time = tA;
float ds = (tB-tA) / (float)(_ViewSamples);
for (int i = 0; i < _ViewSamples; i ++)
{
// Позиция точки
// (сэмплирование в середине отрезка сэмпла видимости)
float3 P = O + D * (time + ds * 0.5);
// T(CP) * T(PA) * ρ(h) * ds
totalViewSamples += viewSampling(P, ds);
time += ds;
}
// I = I_S * β(λ) * γ(θ) * totalViewSamples
float3 I = _SunIntensity * _ScatteringCoefficient * phase * totalViewSamples;The variable is
timeused to track how far we are from the starting point.ds.Optical Thickness PA
Every point on the line of sight
Let's try to simplify this expression, as in the last paragraph. We can further expand the above expression by replacing
Result of skipping over
The combined transmission is modeled as an exponential decrease, the coefficient of which is the sum of the optical thicknesses along the path traveled by light (
The first value that we begin to calculate is the optical thickness of the segment
If we had to implement it “forehead”, then we would create a function
opticalDepththat samples the points betweenopticalDepthSegment), and continue to summarize it in a for ( opticalDepthPA) loop .// Накопитель оптической толщины
float opticalDepthPA = 0;
// Численное интегрирование для вычисления
// влияния света каждой точки P в AB
float time = tA;
float ds = (tB-tA) / (float)(_ViewSamples);
for (int i = 0; i < _ViewSamples; i ++)
{
// Позиция точки
// (сэмплируется посередине сэмпла отрезка видимости)
float3 P = O + D * (time + viewSampleSize*0.5);
// Оптическая толщина текущего отрезка
// ρ(h) * ds
float height = distance(C, P) - _PlanetRadius;
float opticalDepthSegment = exp(-height / _ScaleHeight) * ds;
// Накопление оптических толщин
// D(PA)
opticalDepthPA += opticalDepthSegment;
...
time += ds;
}Light sampling
If we return to the expression for the influence of light
We will move the code that calculates the optical thickness of the segment
lightSampling. The name is taken from a ray of light , which is a segment starting atHowever, the function
lightSamplingdoes not just calculate the optical thickness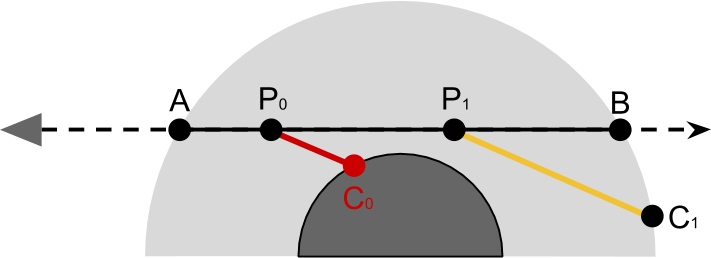
In the diagram below it is easy to see that the influence of light
lightSamplingalso checks for collisions with the planet. This can be done by checking the height of the point for negativity.bool lightSampling
( float3 P, // текущая точка внутри атмосферной сферы
float3 S, // Направление к солнцу
out float opticalDepthCA
)
{
float _; // это нас не интересует
float C;
rayInstersect(P, S, _PlanetCentre, _AtmosphereRadius, _, C);
// Сэмплы на отрезке PC
float time = 0;
float ds = distance(P, P + S * C) / (float)(_LightSamples);
for (int i = 0; i < _LightSamples; i ++)
{
float3 Q = P + S * (time + lightSampleSize*0.5);
float height = distance(_PlanetCentre, Q) - _PlanetRadius;
// Внутри планеты
if (height < 0)
return false;
// Оптическая толщина для луча света
opticalDepthCA += exp(-height / _RayScaleHeight) * ds;
time += ds;
}
return true;
}The function above calculates the point first
rayInstersect. Then she divides the segment_LightSamplesof length ds. The calculation of optical thickness is the same as that used in the outermost loop. The function returns false if a collision with a planet occurs. We can use this to update the missing code of the outermost loop by replacing
.... // D(CP)
float opticalDepthCP = 0;
bool overground = lightSampling(P, S);
if (overground)
{
// Комбинированное пропускание
// T(CP) * T(PA) = T(CPA) = exp{ -β(λ) [D(CP) + D(PA)]}
float transmittance = exp
(
-_ScatteringCoefficient *
(opticalDepthCP + opticalDepthPA)
);
// Влияния света
// T(CPA) * ρ(h) * ds
totalViewSamples += transmittance * opticalDepthSegment;
}Now that we have taken into account all the elements, our shader is ready.
[Note per .: on the author’s Patreon page, you can buy access to Standard and Premium versions of the finished shader.]
