October 11, 2017 at 17:00

How to determine the sample size?

  • Tutorial
Statistics know everything. And Ilf and E. Petrov, "12 Chairs"

Imagine that you are building a large shopping center and would like to evaluate the traffic flow of the entrance to the parking area. No, let's give another example ... they will never do this anyway. You need to evaluate the taste preferences of your portal visitors, for which it is necessary to conduct a survey among them. How to correlate the amount of data and the possible error? Nothing complicated - the larger your sample, the smaller the error. However, there are nuances here.


Graphs


Theoretical minimum


It will not be superfluous to refresh memory, these terms will be useful to us further.


  • Population - The set of all objects among which research is being conducted.
  • Sample - A subset, part of the objects from the entire population that is directly involved in the study.
  • A mistake of the first kind - (α) The probability of rejecting the null hypothesis, while it is true.
  • A mistake of the second kind - (β) The probability of not rejecting the null hypothesis, while it is false.
  • 1 - β - Statistical power of the criterion.
  • μ 0 and μ 1 - Average values ​​for the null and alternative hypothesis.

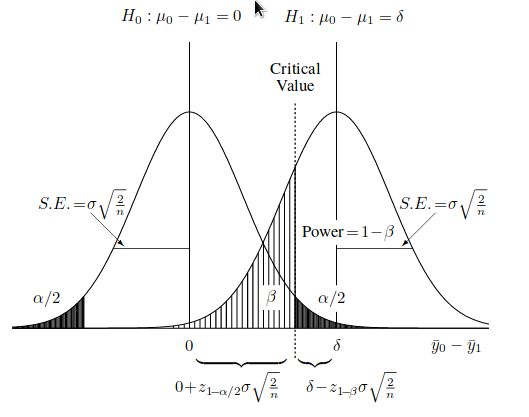
Comparison of two alternative averages


Already in the definitions themselves, errors of the first and second kind have room for debate and interpretation. How to decide with them and which one to choose as zero? If you examine the level of soil or water pollution, how do you formulate the null hypothesis: is there pollution, or is there no pollution? But the sample size from the general population of objects depends on this .


Distribution Characteristics and Standard Deviation


The initial population , as well as the sample, can have any distribution, however, the average value is normal or Gaussian distribution due to the Central Limit Theorem .


Regarding the distribution parameters and the mean value in particular, several types of inferences are possible. The first of these is called the confidence interval . It indicates the interval of possible parameter values, with the specified confidence coefficient . So for example, the 100(1-α)%confidence interval for μ will be like this (Lv. 1).


$ \ hat {\ mu} \ pm t _ {{\ alpha / 2}; df} \ sqrt {\ frac {\ hat \ sigma ^ 2} {n}} $


  • df - Degree of freedom = n - 1, from the English "degrees of freedom".
  • $ t _ {{\ alpha / 2}; df} $- Double-sided critical value t-критерий Стьюдента.

The second inference is a hypothesis test . It could be something like this.


  • H 0 : μ = h
  • H 1 : μ> h
  • H 2 : μ <h

With a confidence interval100(1-α) for μ, one can opt for H 1 and H 2 :


  • If the lower limit of the confidence interval100(1-α) < h , then reject H 0 in favor of H 2 .
  • If the upper limit of the confidence interval is100(1-α) > h, then we reject H 0 in favor of H 1 .
  • If the confidence interval100(1-α) includes h, then we cannot reject H 0 and such a result is considered undefined .

If we need to check the value of μ for one sample from the total population, then the criterion will take the form.


  • Discard H 0 and accept H 1 : μ> h if$ t> t _ {{\ alpha / 2}; df} $.
  • Discard H 0 and accept H 2 : μ <h if$ t <t _ {{\ alpha / 2}; df} $.
  • It is impossible to reject H 0 if$ | t | <t _ {{\ alpha / 2}; df} $.

Where $ t = (\ hat {\ mu} - h) / \ sqrt \ frac {\ hat \ sigma ^ 2} {n} $.


Confidence Interval, Accuracy, and Sample Size


Take the very first equation and express from there the width of the confidence interval (Lv. 2).


$ w = 2t _ {{\ alpha / 2}; df} \ sqrt {\ frac {\ hat \ sigma ^ 2} {n}} $


In some cases, we can replace t-статистику Стьюдентаwith z стандартного нормального распределения. Another simplification is to replace half of w with the measurement error E. Then our equation will take the form (Lv. 3).


$ E = z _ {\ alpha / 2} \ sqrt {\ frac {\ hat \ sigma ^ 2} {n}} $


As you can see, the error really decreases along with an increase in the amount of input data . From where it is easy to deduce the sought (Lv. 4).


$ n = \ left [\ frac {z _ {\ alpha / 2} * \ sigma} {E} \ right] ^ 2 $


Practice - counting with R


Let us verify the hypothesis that the average value of this sample of the number of insects in the trap is 1.


  • H 0 : μ = 1
  • H 1 : μ> 1

Insects0123456
Traps10955121

> x <- read.table("/tmp/tcounts.txt")
> y = unlist(x, use.names="false")
> mean(z);sd(z)
[1] 1.636364
[1] 1.654883

Note that the mean and standard deviation are almost equal, which is natural for the Poisson distribution. 95% confidence interval for t-статистики Стьюдентаand df=32.


> qt(.975, 32)
[1] 2.036933

and finally we get the critical interval for the average value: 1.05 - 2.22 .


> μ=mean(z)
> st = qt(.975, 32)
> μ + st * sd(z)/sqrt(33)
[1] 2.223159
> μ - st * sd(z)/sqrt(33)
[1] 1.049568

As a result, H 0 should be rejected and H 1 should be taken, since with a probability of 95%, μ > 1.


В том же самом примере, если принять, что нам известно действительное стандартное отклонение — σ, а не ее оценка полученная с помощью случайной выборки, можно рассчитать необходимое n для данной погрешности. Посчитаем для E=0.5.


> za2 = qnorm(.975)
> (za2*sd(z)/.5)^2
[1] 42.08144

Поправка на ветер


На самом деле нет никаких причин, полагать, что нам будет известна σ (дисперсия), в то время как μ (среднее) нам еще только предстоит оценить. Из-за этого уравнение 4 имеет мало практической пользы, кроме особо рафинированных примеров из области комбинаторики, а реалистичное уравнение для n несколько сложнее при неизвестной σ (Ур. 5).


$ n = 4 \ tilde \ sigma ^ 2 (z _ {\ alpha / 2} / w) ^ 2 + z ^ 2 _ {\ alpha / 2} / 2 $


Note that σ in the last equation is not with a cap (^), but a tilde (~). This is a consequence of the fact that at the very beginning we do not even have an estimated standard deviation of a random sample -$ \ hat \ sigma $, and instead we use the planned -$ \ tilde \ sigma $. Where do we get the last? We can say that from the ceiling: expert assessment, rough estimates, past experience, etc.


And what about the second term on the right side of the 5th equation, where did it come from? Because$ z _ {\ alpha / 2} <t _ {{\ alpha / 2}; df} $Gunter amendment is needed .


In addition to equations 4 and 5, there are several more approximate formulas, but this already deserves a separate post.


Used materials


  1. Sample sizes
  2. Hypothesis testing
Tags:

Also popular now: