Neural network optimization methods
In the overwhelming majority of sources of information about neural networks, “now let's train our network” means “feed the target function to the optimizer” with only minimal tuning of the learning speed. It is sometimes said that updating the network weights can be not only a stochastic gradient descent, but without any explanation, what is remarkable, and other algorithms that mean mysterious and
their parameters. Even teachers in machine learning courses often do not focus on this. I would like to correct the lack of information in RuNet about various optimizers that you may come across in modern machine learning packages . I hope my article will be useful to people who want to deepen their understanding of machine learning or even invent something of their own.

Under the cut a lot of pictures, including animated gifs.
The article is aimed at a reader familiar with neural networks. It is assumed that you already understand the essence of backpropagation and SGD . I will not go into a rigorous proof of the convergence of the algorithms presented below, but rather, I will try to convey their ideas in simple language and show that the formulas are open for further experiments. The article lists far from all the difficulties of machine learning and not all ways to overcome them.
Why tricks are needed
Let me remind you how the formulas for the usual gradient descent look:
where are the network parameters,
is the objective function or loss function in the case of machine learning, and
is the learning rate. It looks surprisingly simple, but a lot of magic is hidden in
- updating the parameters of the output layer is quite simple, but in order to get to the parameters of the layers behind it, you have to go through non-linearities, the derivatives of which contribute. This is the familiar backpropagation principle of error propagation.
The explicitly written formulas for updating the scales somewhere in the middle of the network look scary, because each neuron depends on all the neurons with which it is connected, and those on all the neurons with which they are connected, and so on. Moreover, even in “toy” neural networks there can be about 10 layers, and among networks that hold the Olympus of classification of modern datasets - much, much more. Each weight is a variable in . Such an incredible number of degrees of freedom allows you to build very complex mappings, but it brings researchers a headache:
- Jam at local minima or saddle points, of which there
can be a lot of variables for a function of variables.
- The complex landscape of the objective function: plateaus alternate with regions of strong non-linearity. The derivative on the plateau is almost zero, and a sudden break, on the contrary, can send us too far.
- Some parameters are updated much less often than others, especially when informative, but rare signs are found in the data, which adversely affects the nuances of the generalizing network rule. On the other hand, giving too much importance to all rarely encountered signs in general can lead to retraining.
- Too slow learning speed makes the algorithm converge for a very long time and get stuck in local lows, too fast to “fly through” narrow global lows or even diverge
Computational mathematics knows advanced second-order algorithms that can find a good minimum on a difficult terrain, but then the number of weights strikes again. To use the honest second-order “head-on” method, you have to calculate the Hessian - the matrix of derivatives for each pair of parameters of a pair of parameters (already bad) - and, say, for the Newton method, also the inverse of it. We have to invent all sorts of tricks to cope with problems, leaving the task computationally uplifting. Second-order working optimizers do exist , but for now, let's concentrate on what we can achieve without considering the second derivatives.
Nesterov Accelerated Gradient
The idea of methods with the accumulation of momentum is obviously simple: “If we move in a certain direction for some time, then we should probably move there for some time in the future.” To do this, you need to be able to refer to the recent history of changes in each parameter. You can store the latest instances
and honestly take the average at each step, but this approach takes up too much memory for large ones
. Fortunately, we do not need an exact average, but only an estimate, so we use an exponential moving average.
In order to accumulate something, we will multiply the already accumulated value by the conservation coefficient and add the next value multiplied by
. The closer
to unity, the larger the accumulation window and the smoother the stronger - the story
begins to influence more than each successive one
. If at
some point, they
decay exponentially, exponentially, hence the name. We apply the exponential running average to accumulate the gradient of the objective function of our network:
Where the order is usually taken
. Note that it is
not lost, but is included in
; sometimes you can also find a version of the formula with an explicit factor. The smaller
, the more the algorithm behaves like a regular SGD. To get a popular physical interpretation of equations, imagine a ball rolling down a hilly surface. If at the moment there
was a non-zero slope (
) under the ball , and then it hit a plateau, it will still continue to roll along this plateau. Moreover, the ball will continue to move a couple of updates in the same direction, even if the bias has changed to the opposite. Nevertheless, viscous friction acts on the ball and every second it loses
its speed. This is what the momentum looks like for different
(hereinafter, the epochs are plotted along the X axis, and the gradient value and accumulated values are plotted along Y ):
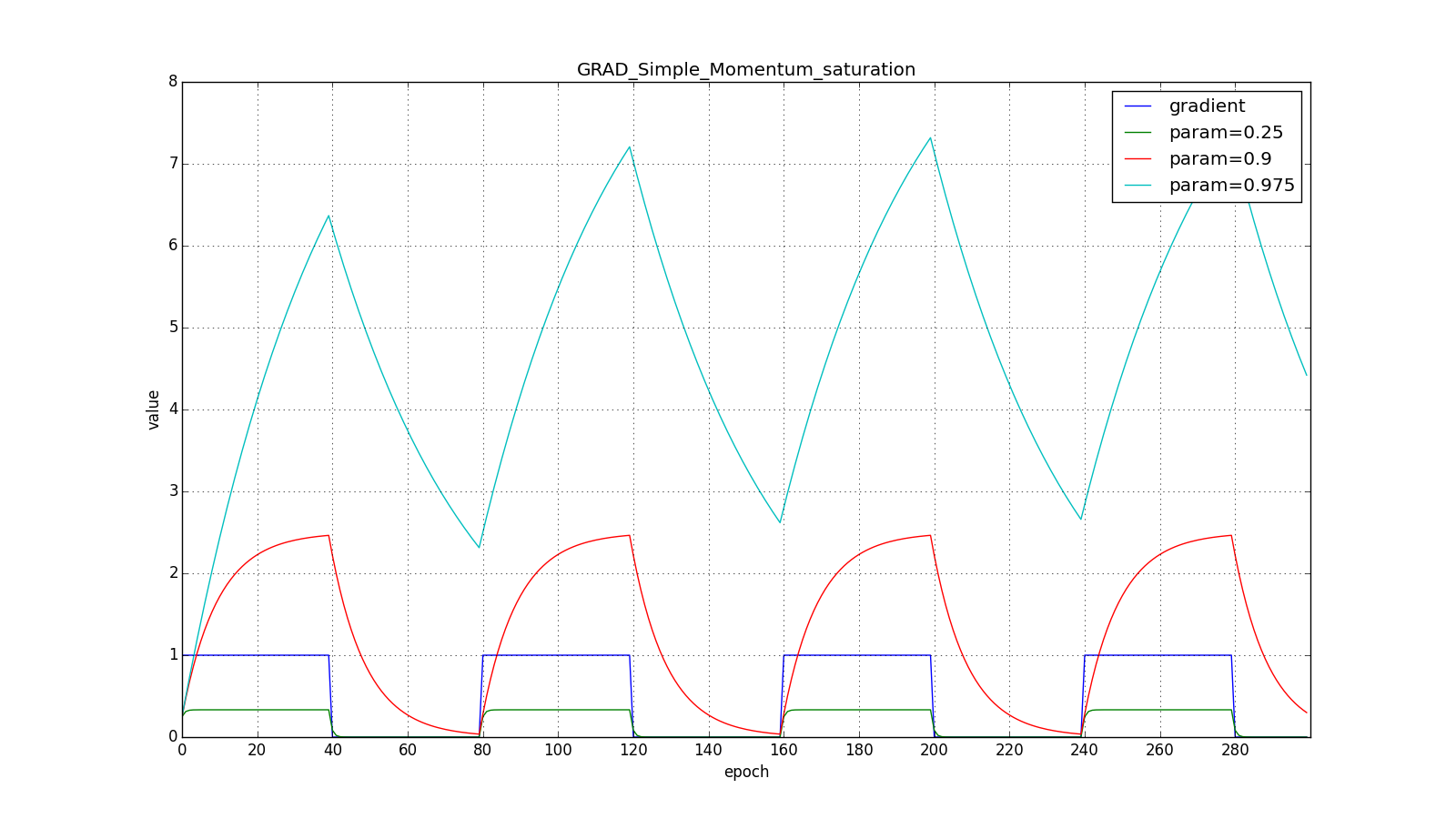
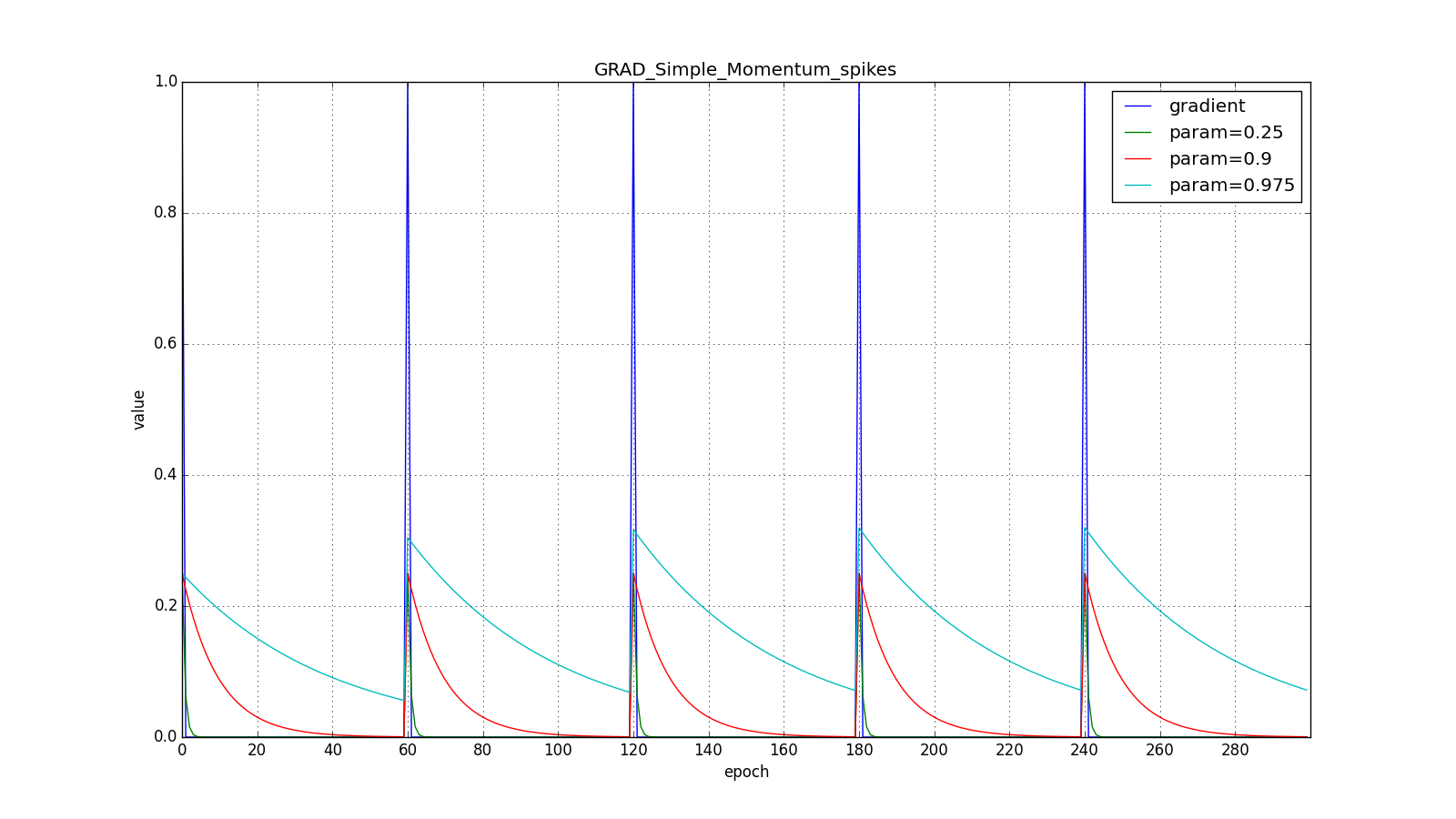
Note that the accumulated value can very much exceed the value of each
. A simple accumulation of momentum already gives a good result, but Nesterov goes further and applies the idea well-known in computational mathematics: looking ahead along the update vector. Since we are still going to shift by
, let's calculate the gradient of the loss function not at a point
, but at
. From here:
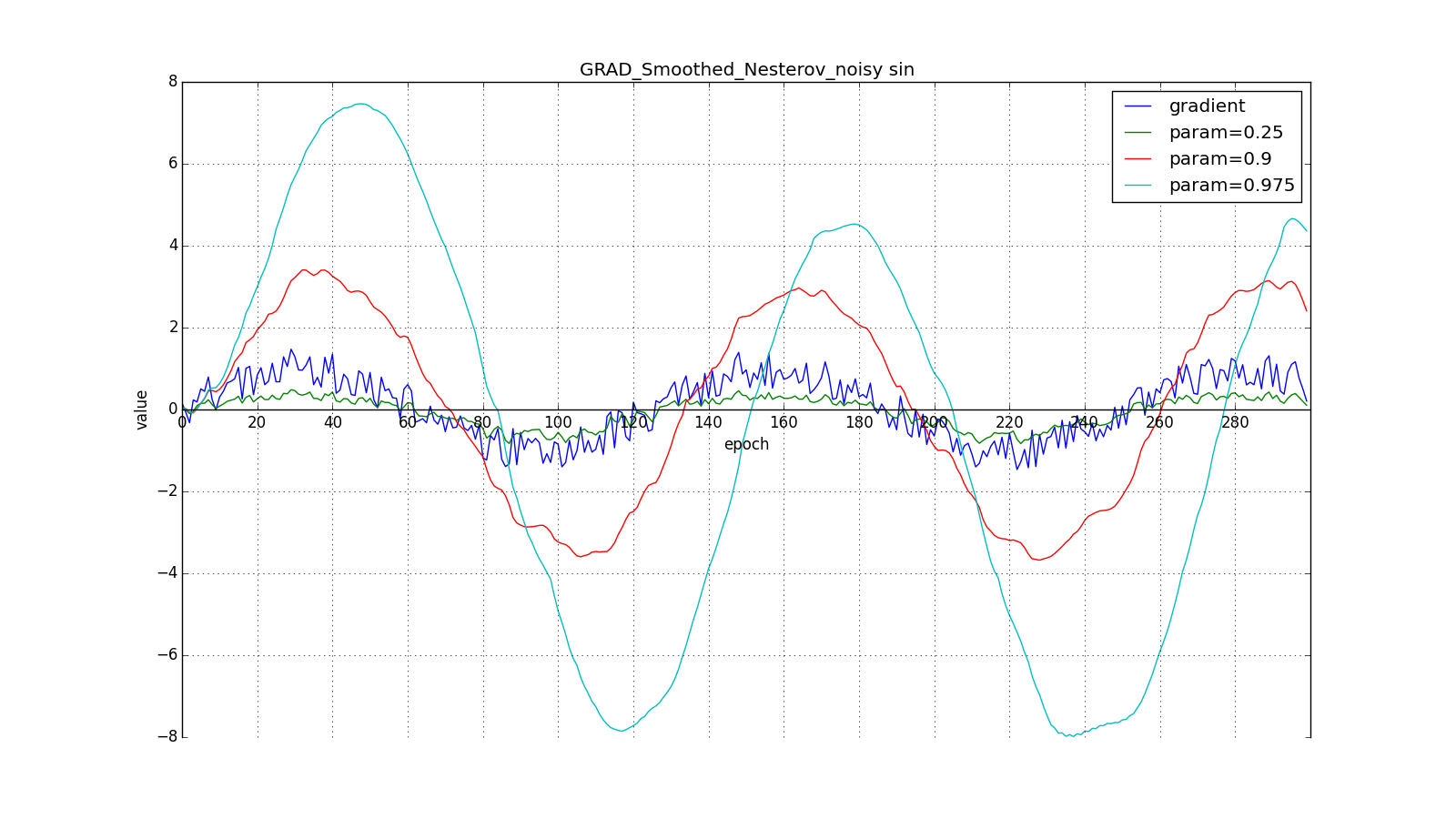
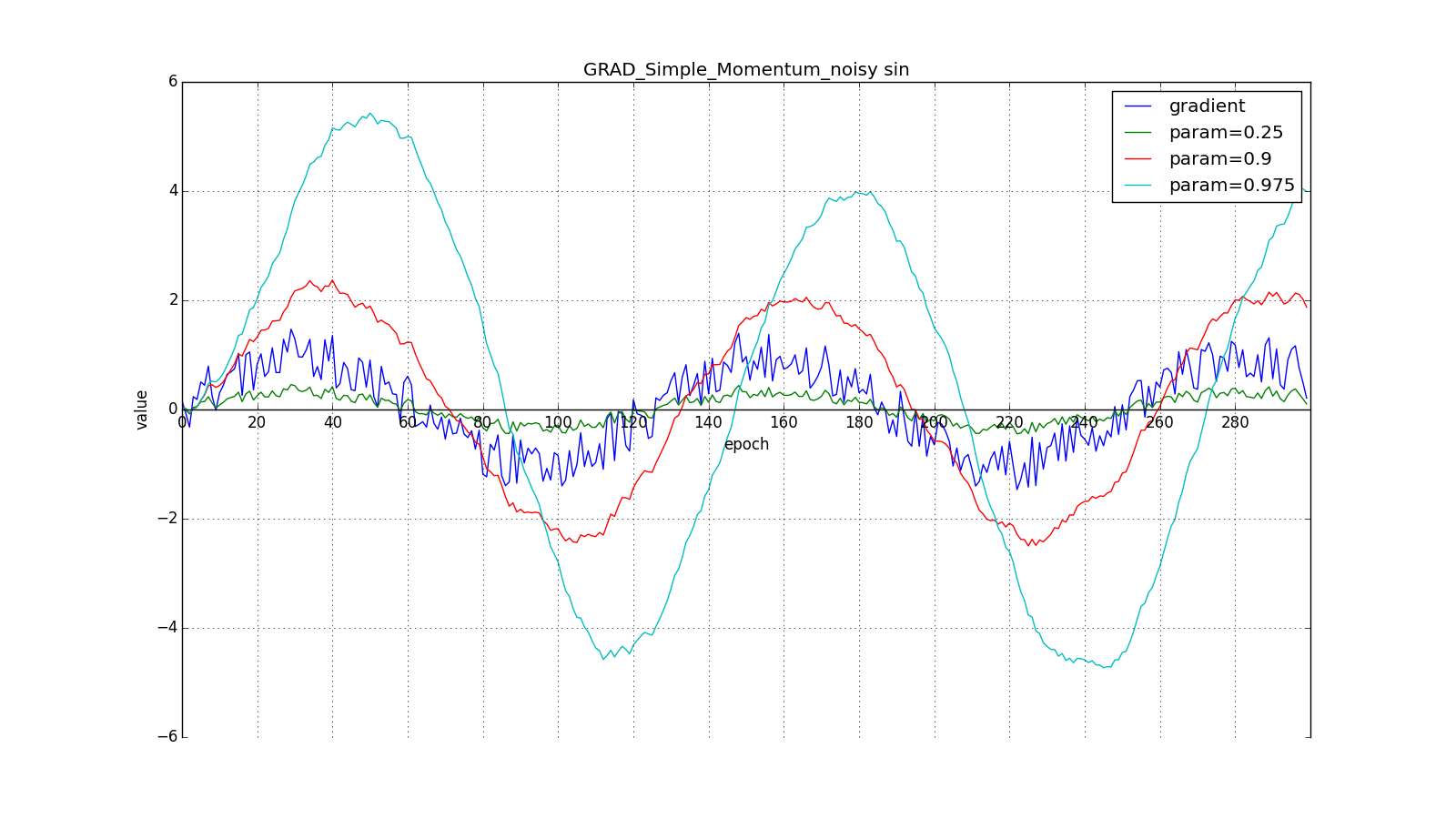
Such a change allows you to “roll” faster if, aside, where we are heading, the derivative increases, and slower, if vice versa. This is especially evident for a graph with a sine.
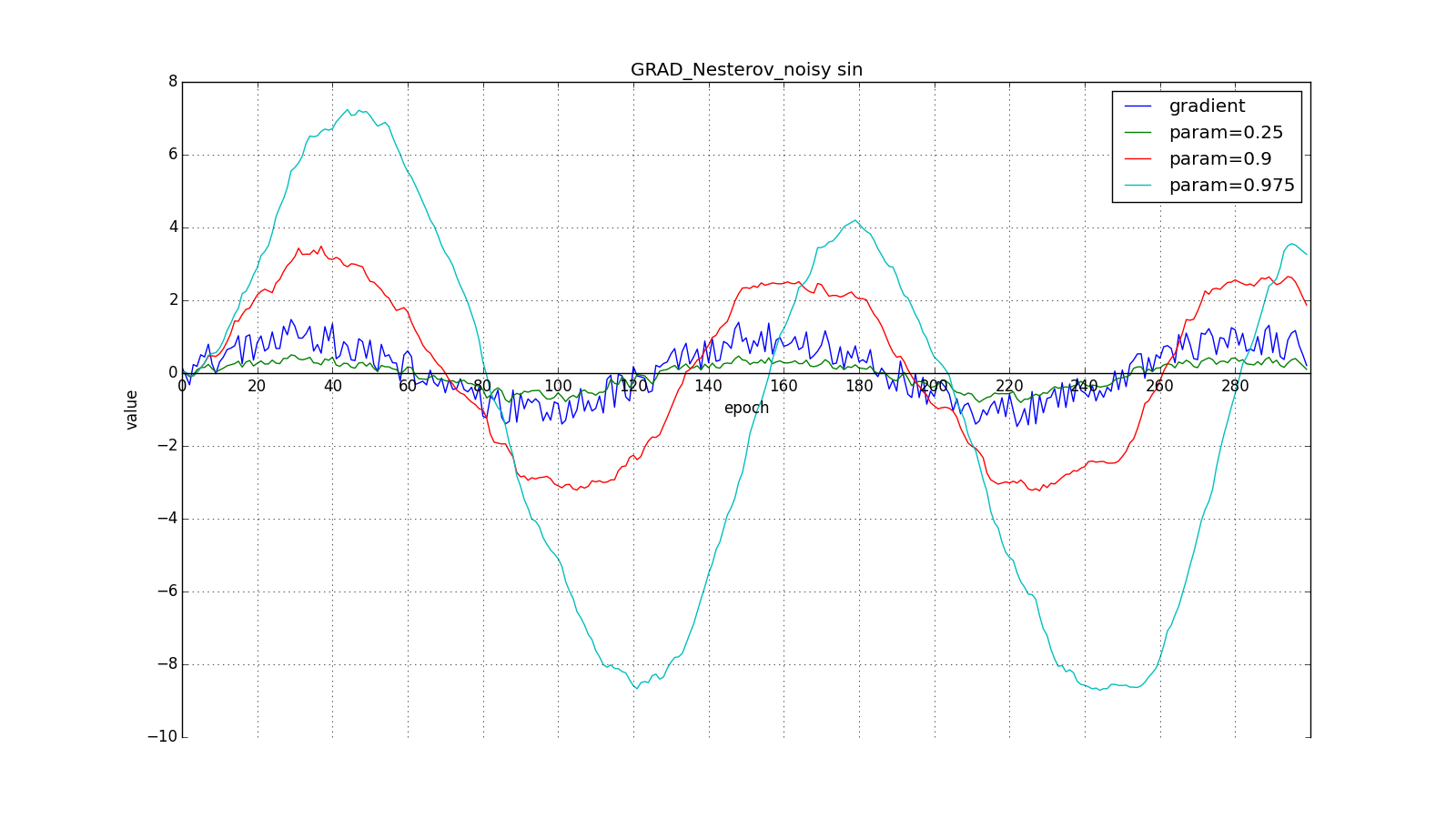
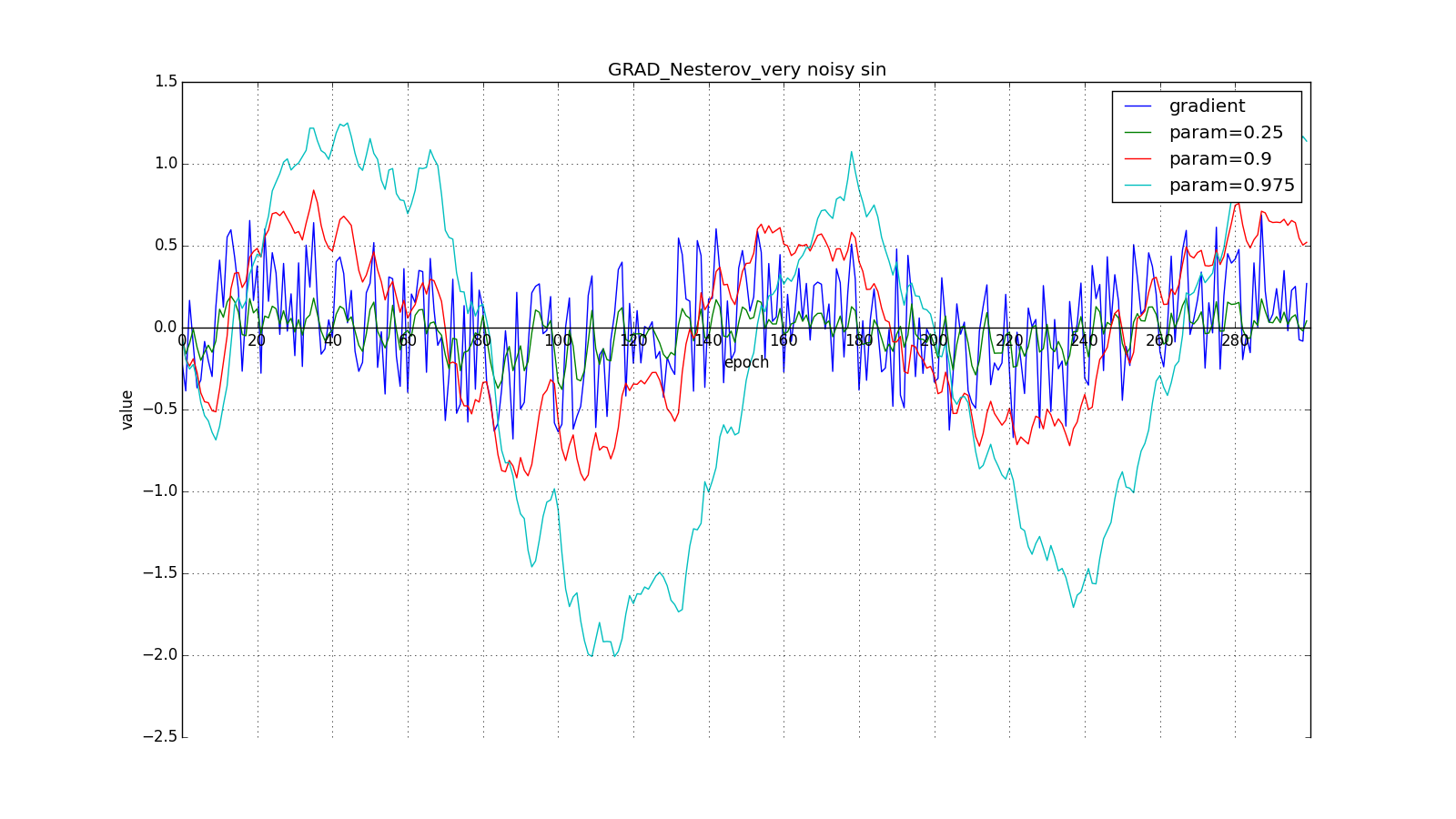
Looking ahead can play a trick with us if you set too large and
: we look so far that we miss areas with the opposite sign of the gradient:

However, sometimes this behavior may be desirable. Once again I will draw your attention to the idea - looking ahead - and not to execution. Nesterov's method (6) is the most obvious option, but not the only one. For example, you can use another trick from computational mathematics - stabilizing the gradient by averaging over several points along the straight line along which we move. So to speak:
Or so:
Such a technique can help in case of noisy target functions.
We will not manipulate the argument of the objective function in subsequent methods (although, of course, no one bothers you with experimenting). Further for brevity
Adagrad
How many methods of accumulation of momentum work, many imagine. Let's move on to more interesting optimization algorithms. Let's start with the relatively simple Adagrad - adaptive gradient.
Some signs may be extremely informative, but rare. Exotic high-paying profession, a fancy word in a spam database - they will easily drown in the noise of all other updates. This is not only about rarely encountered input parameters. Say, you may well meet rare graphic patterns that turn into a sign only after passing through several layers of the convolution network. It would be nice to be able to update the parameters with an eye to how typical a characteristic they are. This is not difficult to achieve: let's keep for each network parameter the sum of the squares of its updates. It will act as a proxy for typicality: if the parameter belongs to a chain of frequently activated neurons, it is constantly pulled back and forth, which means the amount quickly accumulates. We rewrite the update formula like this:
Where is the sum of the squares of the updates, and
is the smoothing parameter necessary to avoid dividing by 0. The parameter often updated in the past has a large parameter
, which means a large denominator in (12). The parameter that changes only once or twice will be updated in full force.
they take order
or
for a very aggressive update, but, as can be seen from the graphs, this plays a role only at the beginning, closer to the middle the training begins to outweigh
:
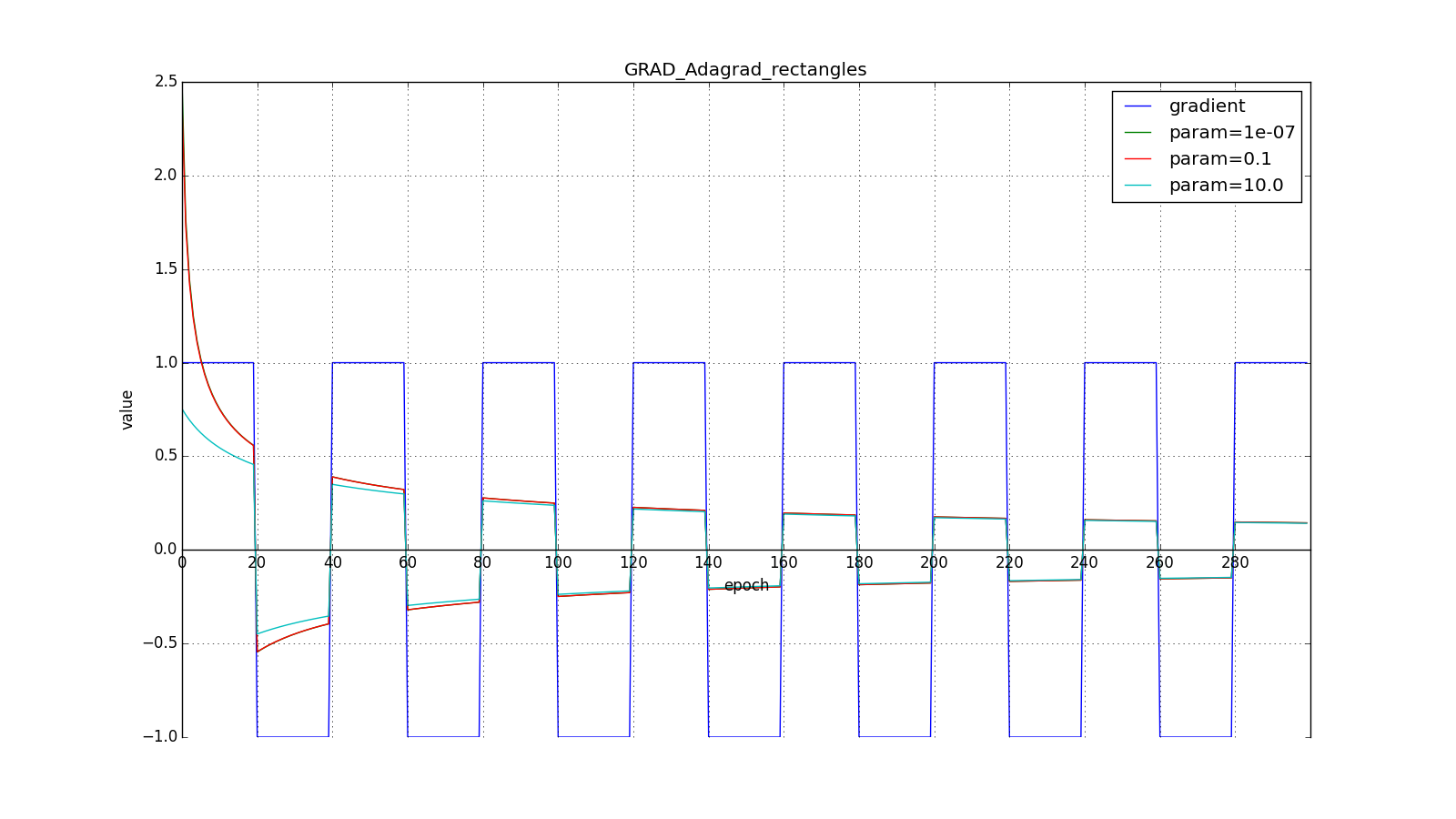
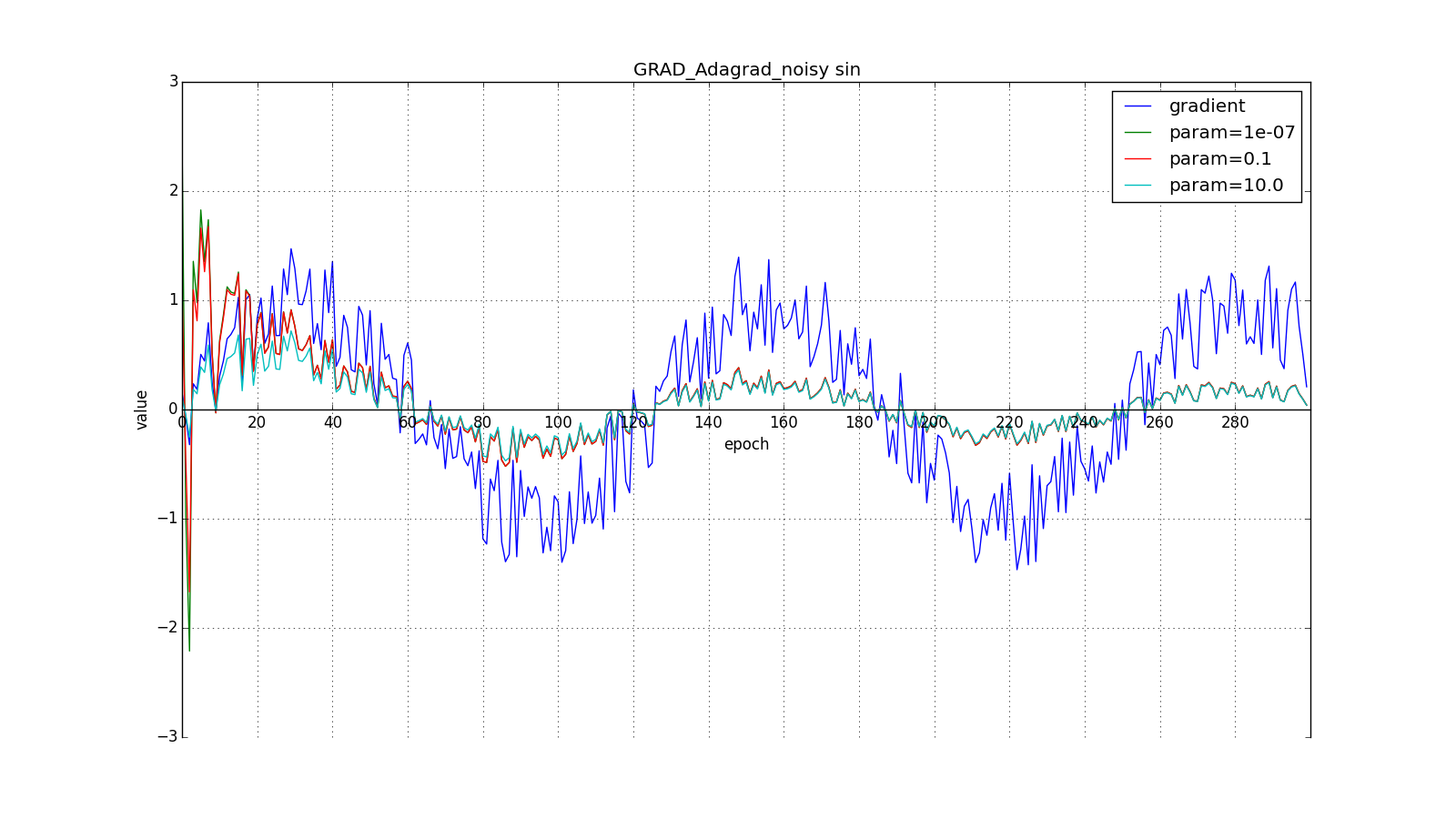
So Adagrad’s idea is to use something to reduce updates for items that we update so often. Nobody forces us to use this formula specifically, therefore Adagrad is sometimes called a family of algorithms. Let's say we can remove the root or accumulate not the squares of updates, but their modules, or even replace the multiplier with something like that .
(Another thing is that this requires experimentation. If you remove the root, updates will begin to decrease too quickly, and the algorithm will deteriorate)
Another advantage of Adagrad is the lack of the need to accurately choose the speed of training. It is enough to put it in a measure large enough to provide a good supply, but not so huge that the algorithm diverges. In fact, we automatically get the attenuation of the learning rate (learning rate decay).
RMSProp and Adadelta
The disadvantage of Adagrad is that in (12) it can increase as much as desired, which after a while leads to too small updates and paralysis of the algorithm. RMSProp and Adadelta are designed to fix this shortcoming.
We are modifying the idea of Adagrad: we are still going to update less weight, which are updated too often, but instead of the full amount of updates, we will use the history-averaged gradient square. We again use the exponentially decaying running average
(4). Let be the running average at the moment
then instead of (12) we get
The denominator is the root of the mean square gradients, hence RMSProp - root mean square propagation
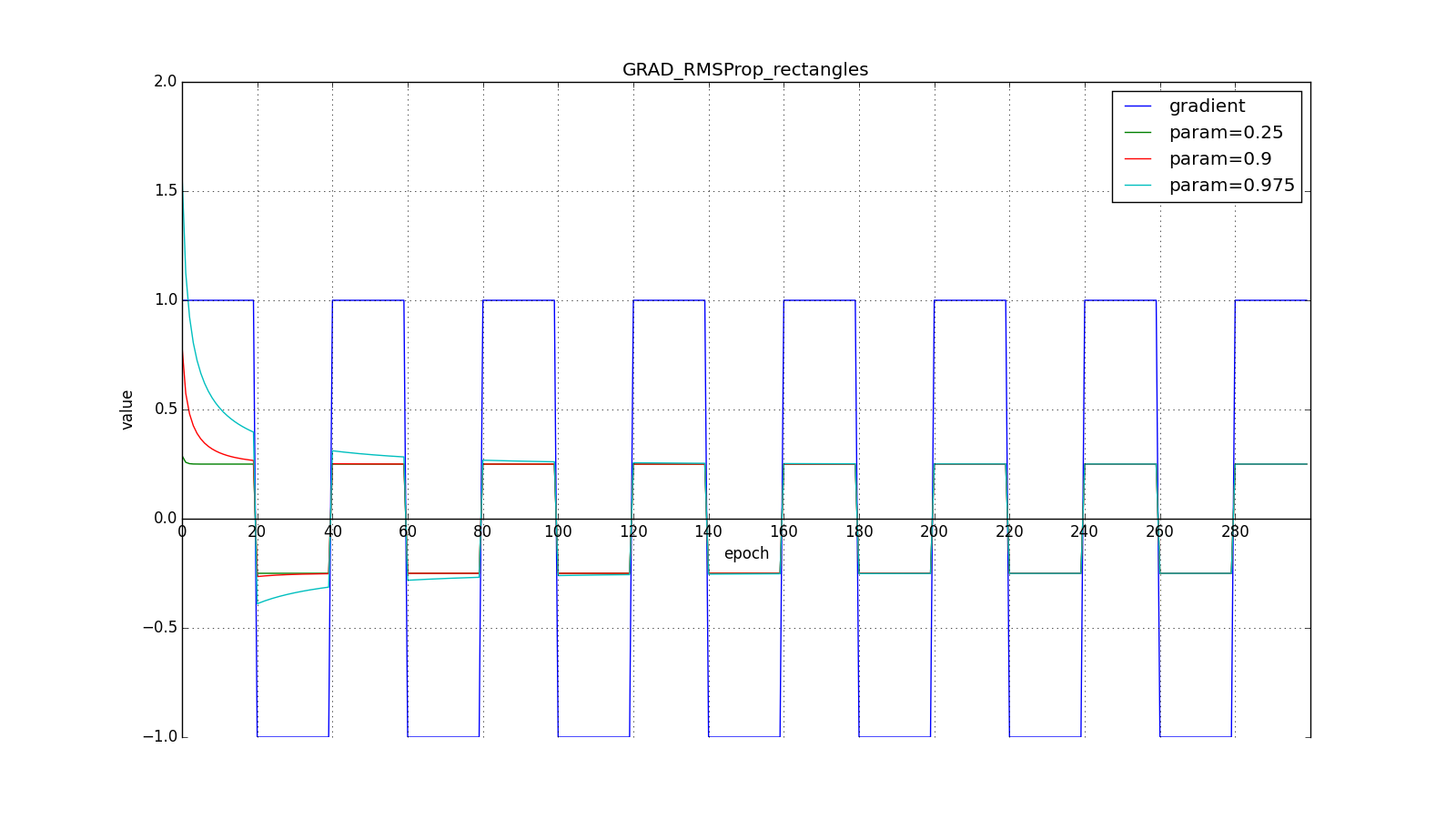
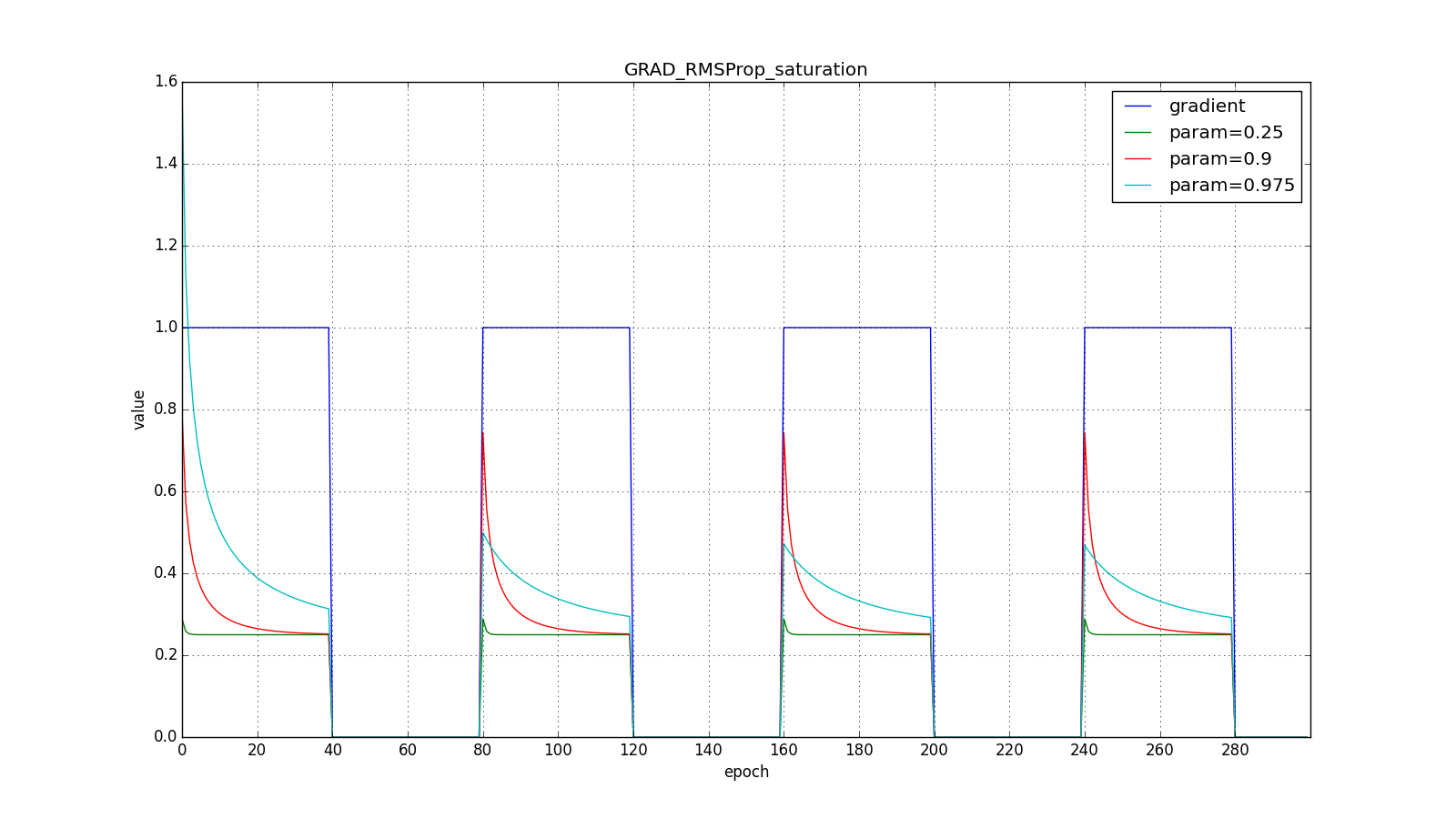

Notice how the refresh rate is restored on the chart with long teeth for different ones . Also compare the graphs with the meander for Adagrad and RMSProp: in the first case, updates are reduced to zero, and in the second they go to a certain level.
That's the whole RMSProp. Adadelta differs from it in that we add to the numerator (14) the stabilizing term proportional to
. At the step,
we still do not know the value
, therefore the parameters are updated in three stages, and not in two: first we accumulate the gradient square, then update
, and then update
.
Such a change is made for reasons of that dimension and
should be the same. Note that the learning rate does not have a dimension, which means that in all the algorithms before that, we added the dimension value to the dimensionless one. Physicists in this place are horrified, and we shrug: it works.
Note that we need a non-zero for the first step, otherwise all subsequent ones
, and therefore
will be equal to zero. But we solved this problem even earlier, adding in
. It’s another matter that without obvious big
we get the behavior opposite to Adagrad and RMSProp: we will be stronger (to a certain limit) to update weights that are used more often . Indeed, now to
become significant, the parameter must accumulate a large amount in the numerator of the fraction.
Here are the graphs for zero starting :

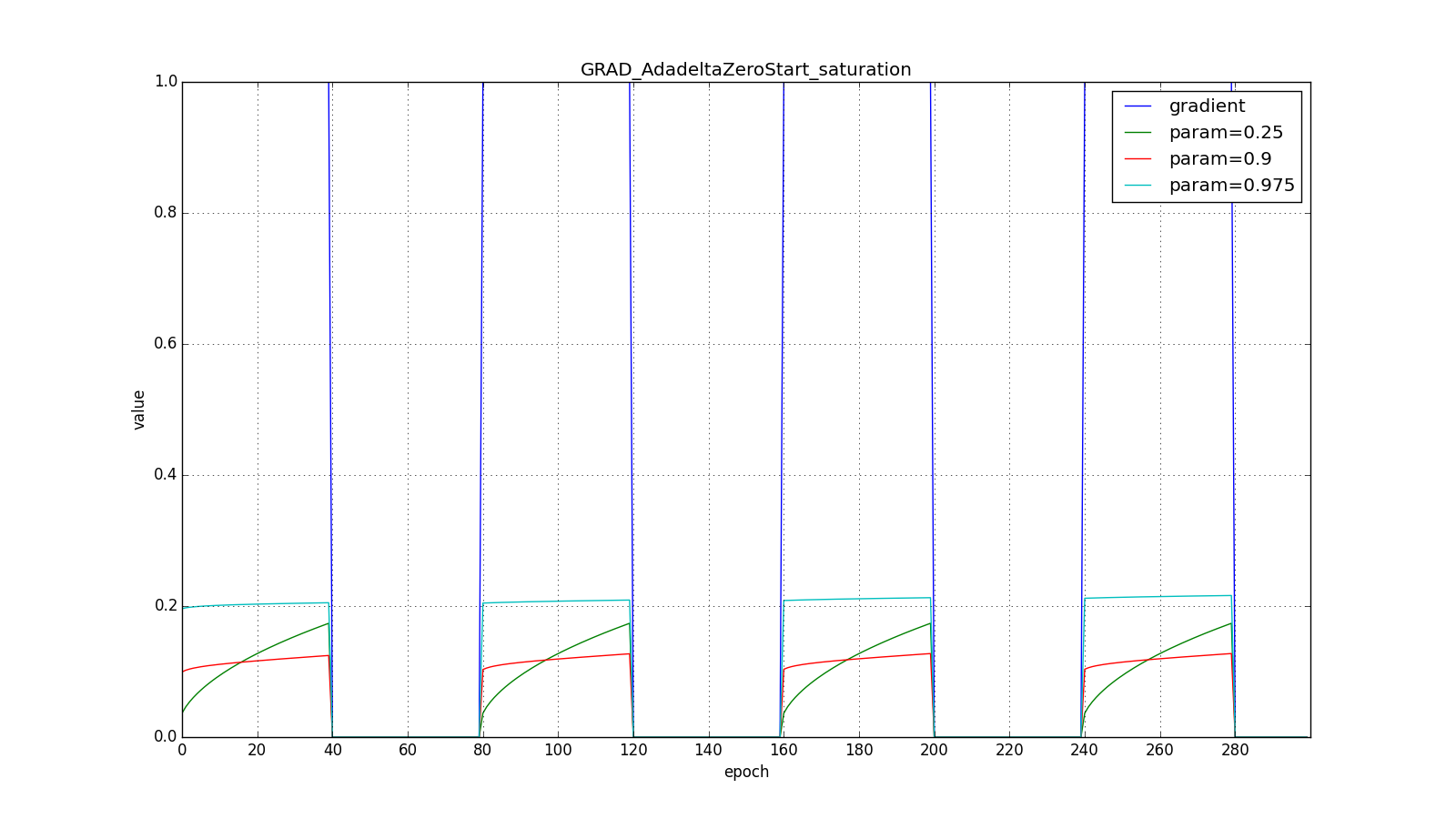
But for the big one:
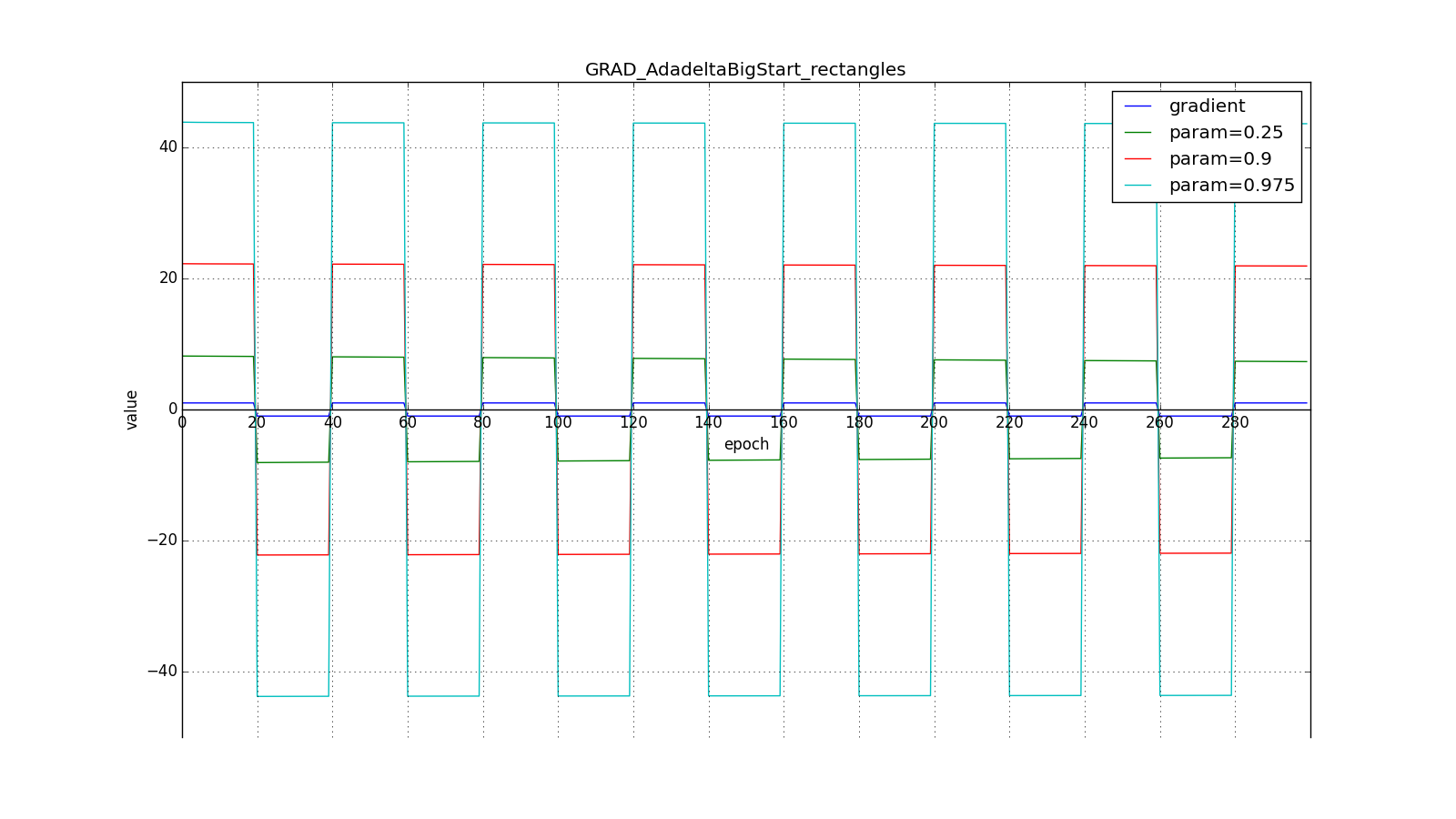
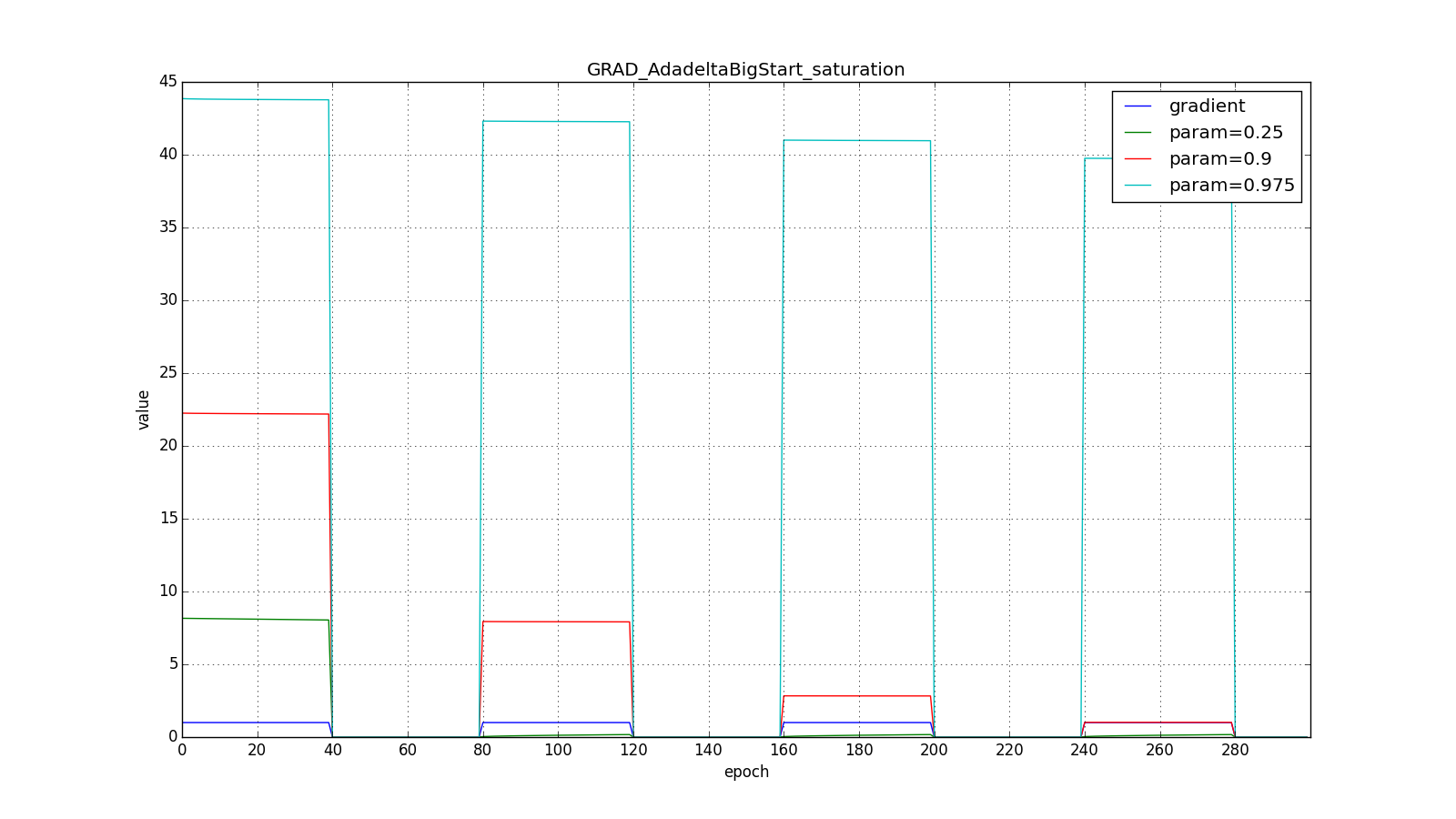
However, it seems that the authors of the algorithm achieved this effect. For RMSProp and Adadelta, as well as for Adagrad, you do not need to very accurately select the learning speed - just an approximate value. It is usually advised to start fitting c
,
and leave it that way
. The closer
to
, the longer RMSProp and Adadelta with large
will greatly update under- used weights. If
so
, then Adadelta will for a long time “with distrust” relate to rarely used scales. The latter can lead to paralysis of the algorithm, or it can intentionally cause “greedy” behavior when the algorithm first updates the neurons encoding the best signs.
Adam
Adam is an adaptive moment estimation, another optimization algorithm. It combines the idea of the accumulation of motion and the idea of a weaker updating of the scales for typical signs. Recall again (4):
Adam differs from Nesterov in that we do not accumulate , but the values of the gradient, although this is a purely cosmetic change, see (23). In addition, we want to know how often the gradient changes. The authors of the algorithm proposed for this to evaluate the average noncentered variance:
It is easy to see that this is already familiar to us , so in fact there are no differences from RMSProp.
An important difference is in the initial calibration and
: they suffer from the same problem as
in RMSProp: if you set a zero initial value, they will accumulate for a long time, especially with a large accumulation window (
,
), and some initial values are still two hyperparameters. No one wants another two hyperparameters, so we artificially increase
and
the first steps (approximately
for
and
for
)
As a result, the update rule:
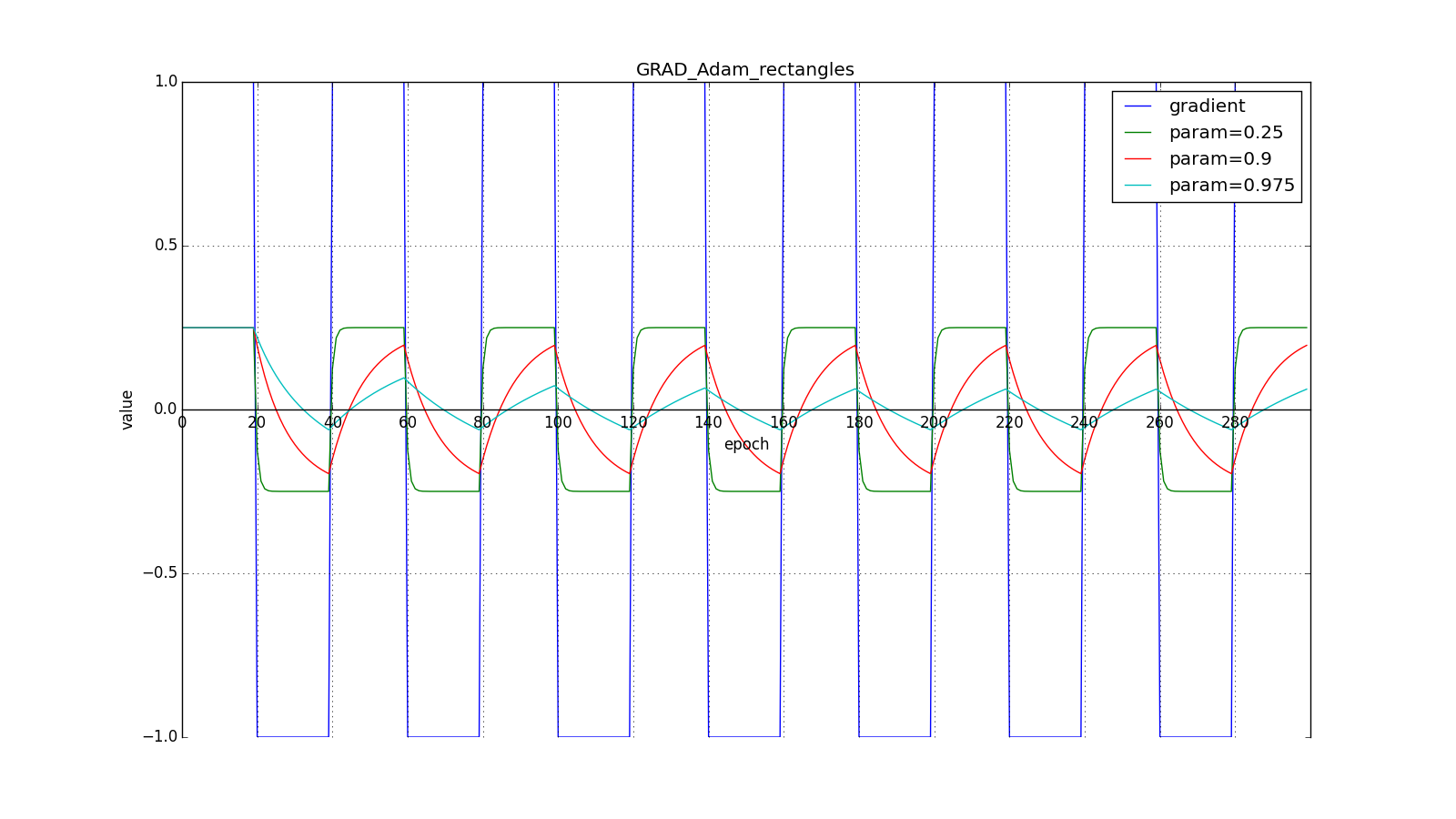
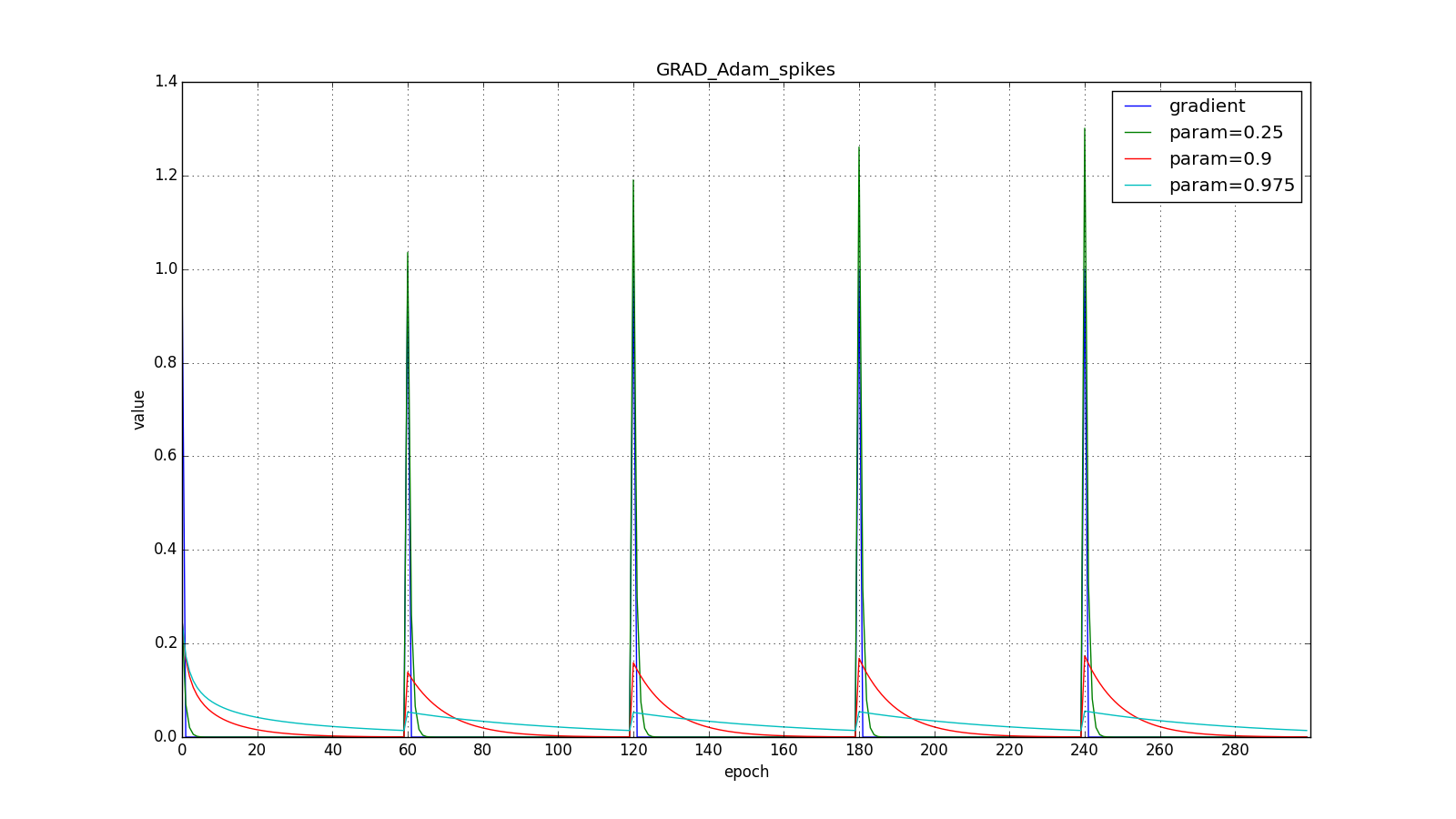
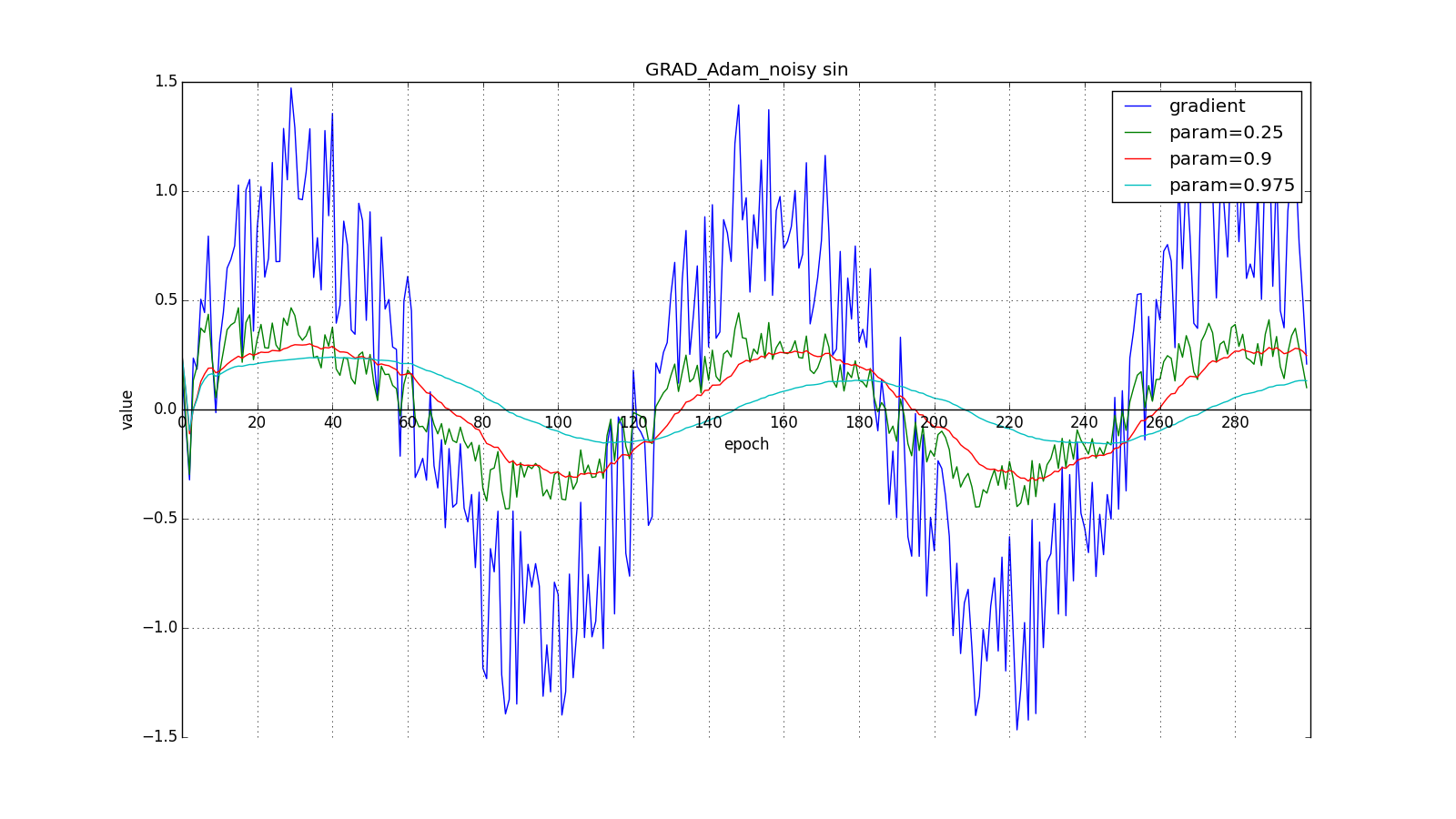
Here you should carefully look at how quickly the update values on the first teeth of the graphs with the rectangles were synchronized and on the smoothness of the update curve on the graph with a sine — we received it “for free”. With the recommended parameter on the graph with spikes, it is clear that sharp bursts of the gradient do not cause an instant response in the accumulated value, therefore well-tuned Adam does not need gradient clipping.
The authors of the algorithm derive (22) by expanding the recursive formulas (20) and (21). For example, for :
The term is close to
with a stationary distribution
, which is not true in cases of practical interest to us. but we still move the bracket from
left. Informally, we can imagine that with
us an endless history of identical updates:
When we get closer to the correct value , we make the “virtual” part of the series fade out faster:
Adam authors propose default values and claim that the algorithm performs better or approximately the same as all previous algorithms on a wide range of datasets due to the initial calibration. Note that again, equations (22) are not carved into stone. We have some theoretical justification why the attenuation should look like this, but no one forbids experimenting with calibration formulas. In my opinion, it just begs to apply looking ahead, as in the Nesterov method.
Adamax
Adamax is just such an experiment, proposed in the same article. Instead of dispersion, in (21) we can consider the inertial moment of the distribution of gradients of an arbitrary degree . This can lead to instability in computing. However, a case
tending to infinity works surprisingly well.
Note that a suitable dimension is used instead
. Also, pay attention to use Adam value formulas obtained in (27), to be taken from his root:
. We derive the decision rule instead of (21), taking
, unfolding under the root
with the help of (27):
This happened because when in the sum in (28) the largest term will dominate. Informally, you can intuitively understand why this is so, taking a simple sum and great
:
. Not at all scary.
The remaining steps of the algorithm are the same as in Adam.
Experiments
Now let's look at different algorithms in action. To make it clearer, let's look at the trajectory of the algorithms in the problem of finding the minimum of the function of two variables. Let me remind you that training a neural network is essentially the same, but there are significantly more than two variables and instead of an explicitly defined function, we only have a set of points on which we want to build this function. In our case, the loss function is the objective function along which optimizers move. Of course, in such a simple task it is impossible to feel the full power of advanced algorithms, but intuitively.
First, let's look at the accelerated Nesterov gradient with different values . Having understood why they look like this, it’s easier to understand the behavior of all other algorithms with the accumulation of momentum, including Adam and Adamax.

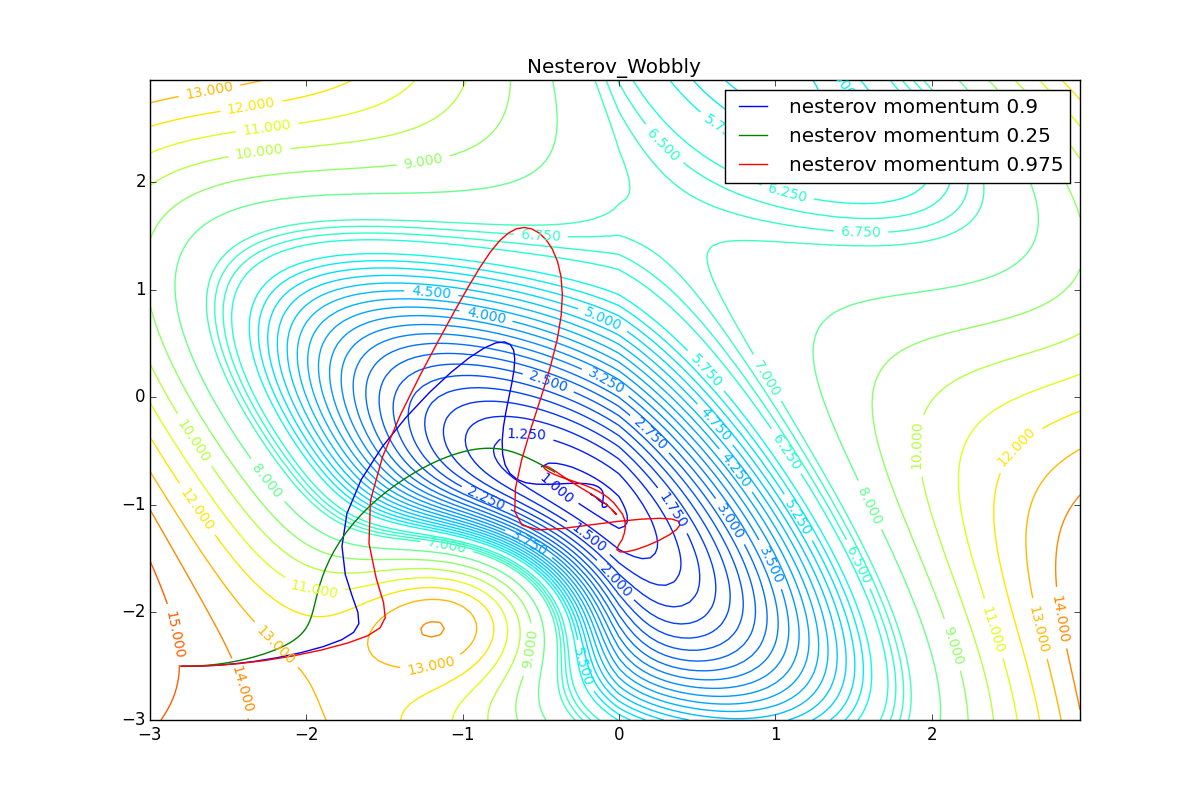
All trajectories end in the same pool, but they do it differently. With a small algorithm, it becomes like a regular SGD, at each step the descent goes towards a decreasing gradient. With too much
, the history of changes begins to strongly influence, and the trajectory can "walk" strongly. Sometimes this is good: the larger the accumulated momentum, the easier it is to break out of the troughs of local minima on the way.
Sometimes it’s bad: you can easily lose momentum by slipping into the hollow of a global minimum and settle in a local one. Therefore, for large ones, one can sometimes see how the losses on the training set first reach a global minimum, then increase very much, then again begin to drop, but never return to the past minimum.
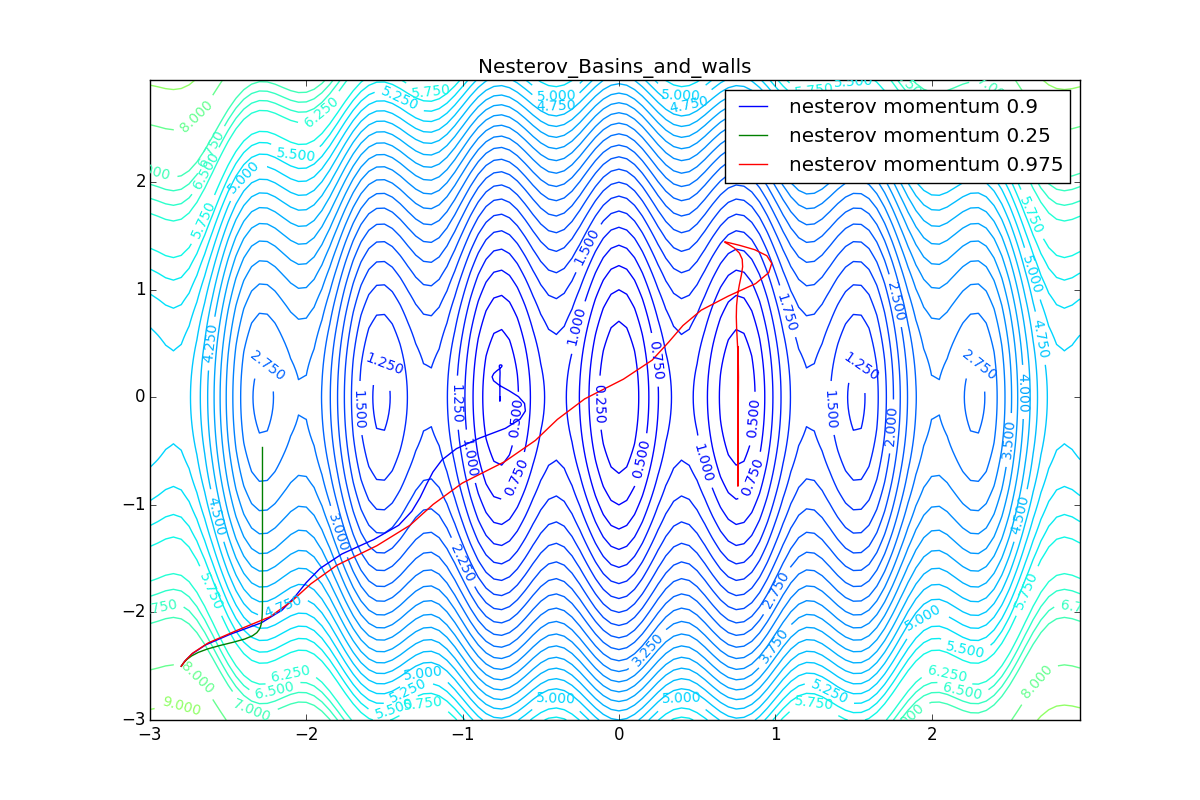
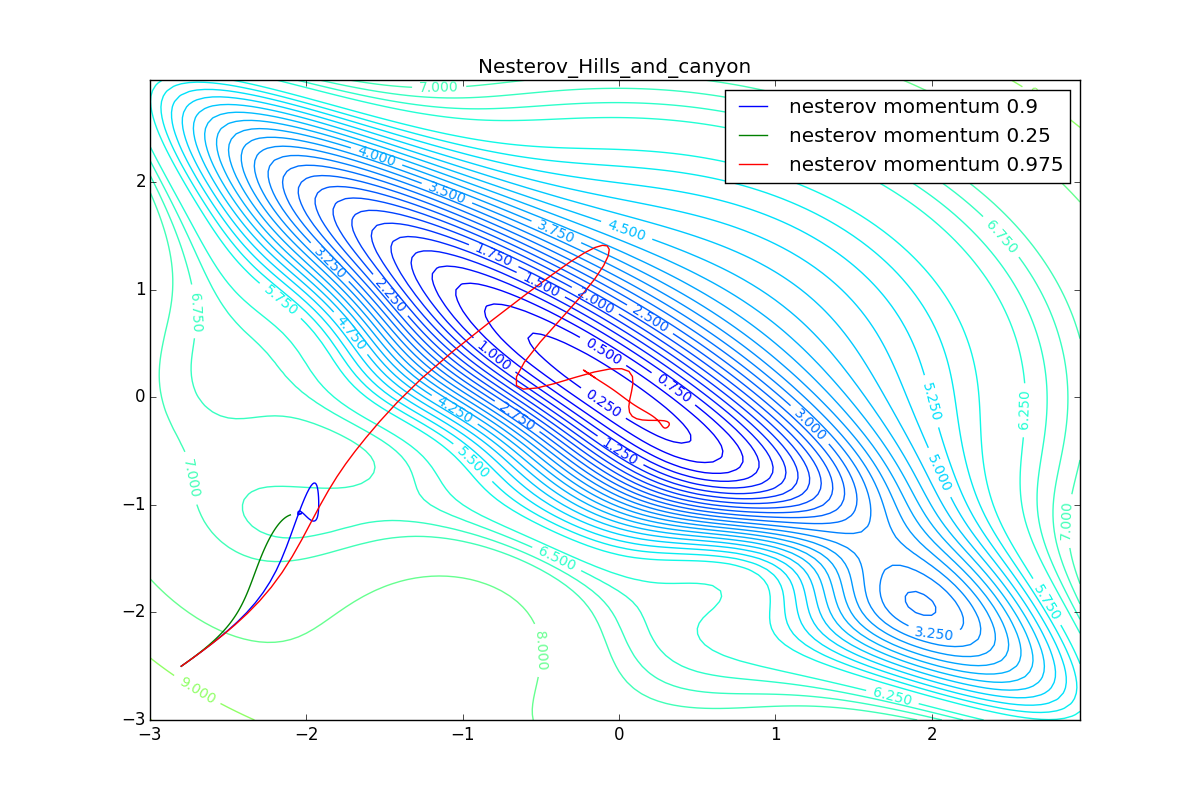
Now we will consider the different algorithms launched from one point.
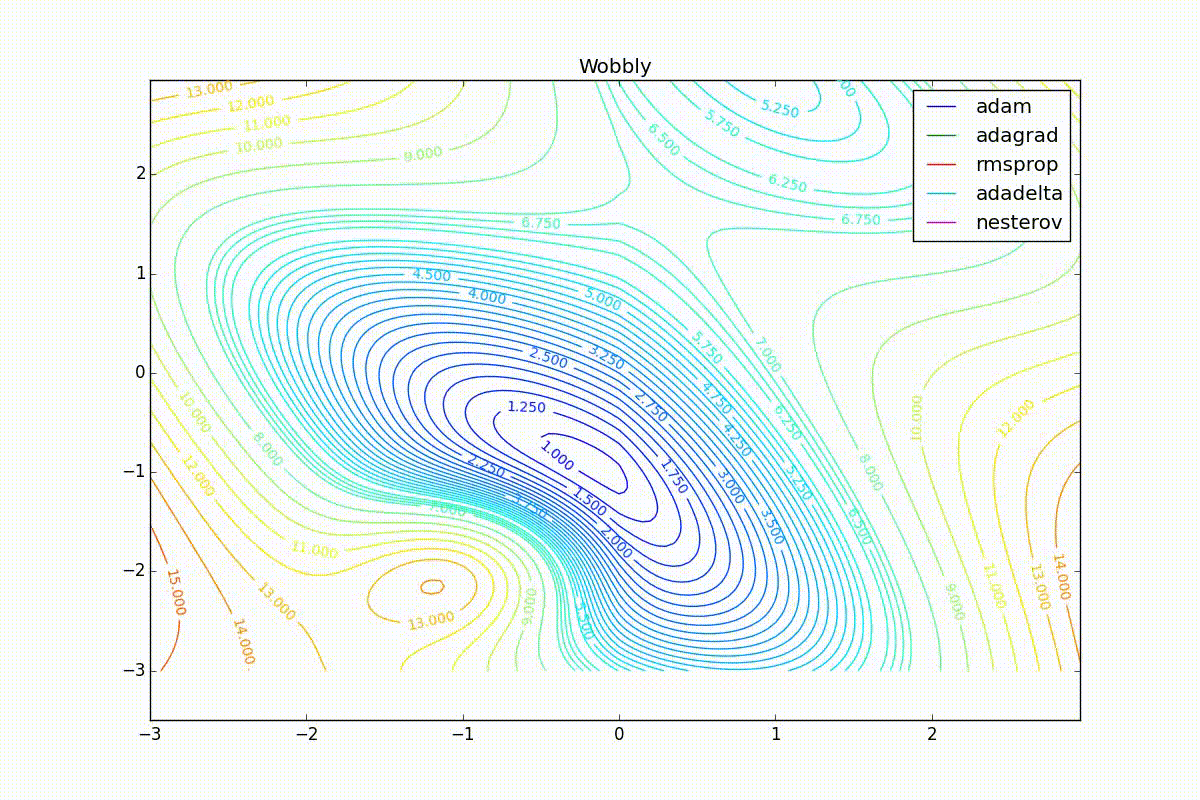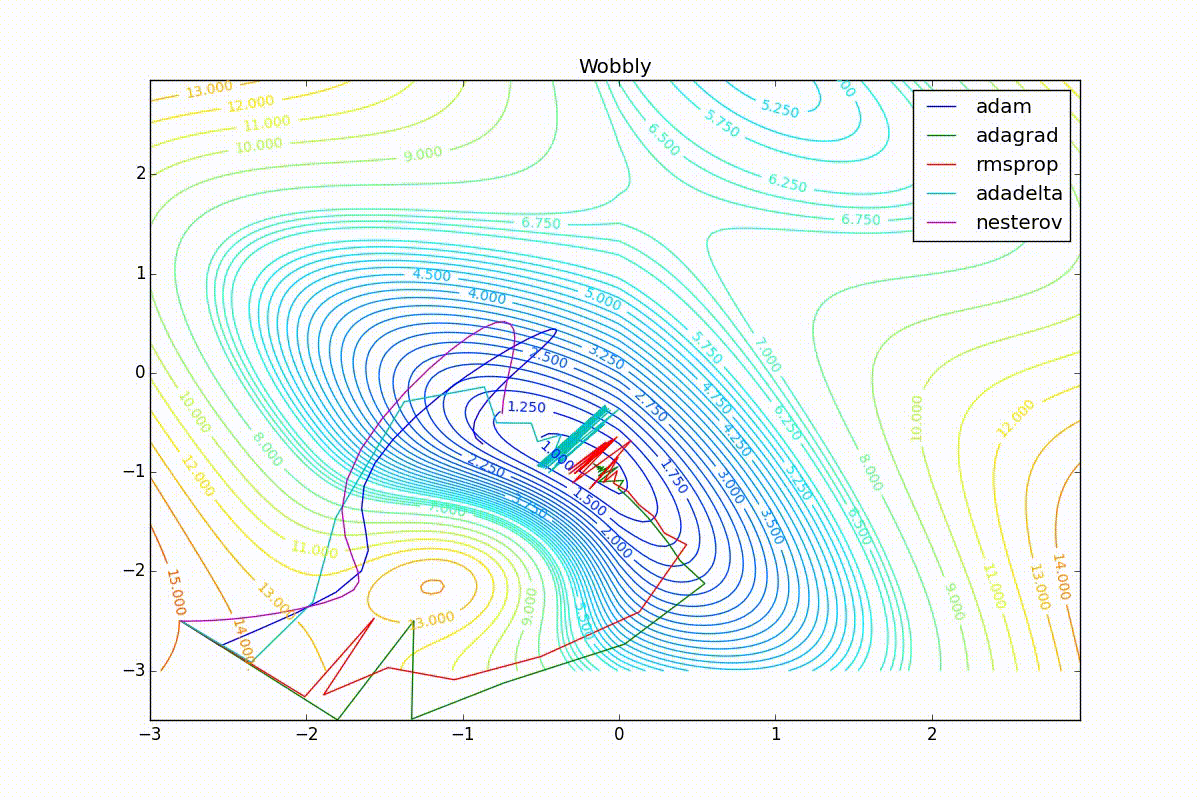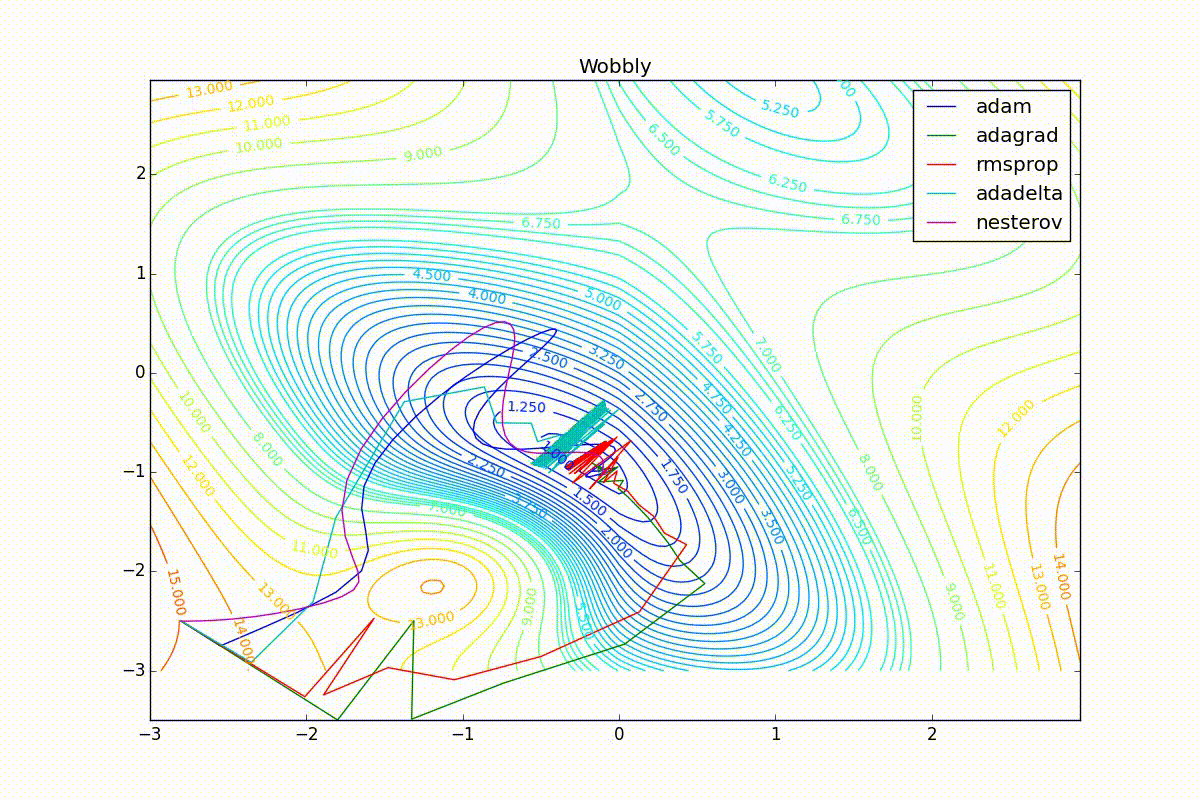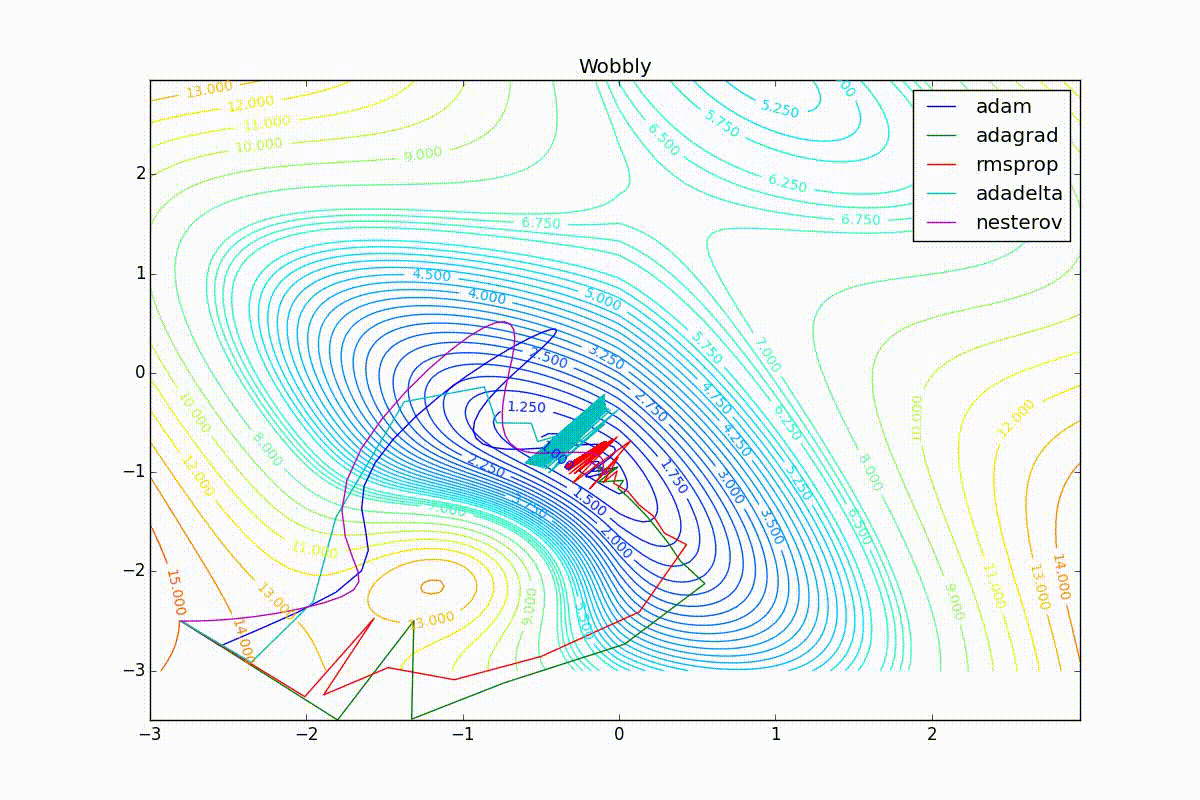
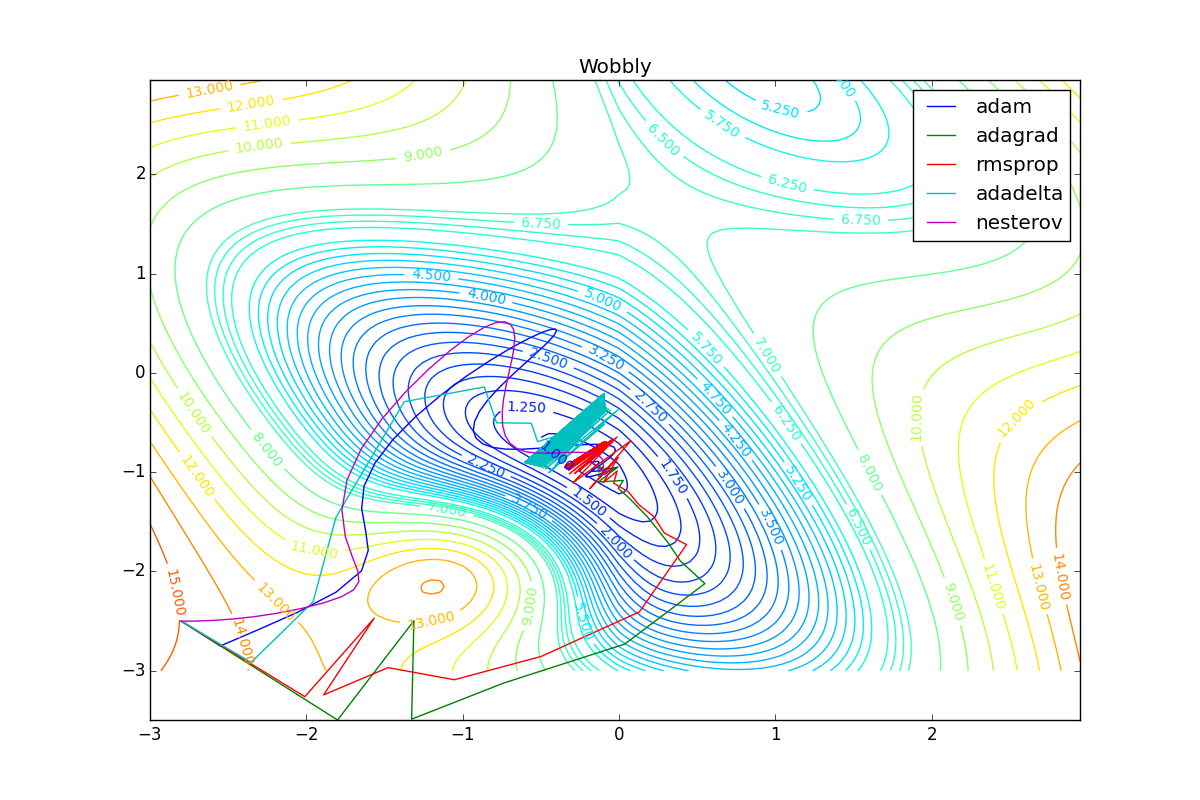
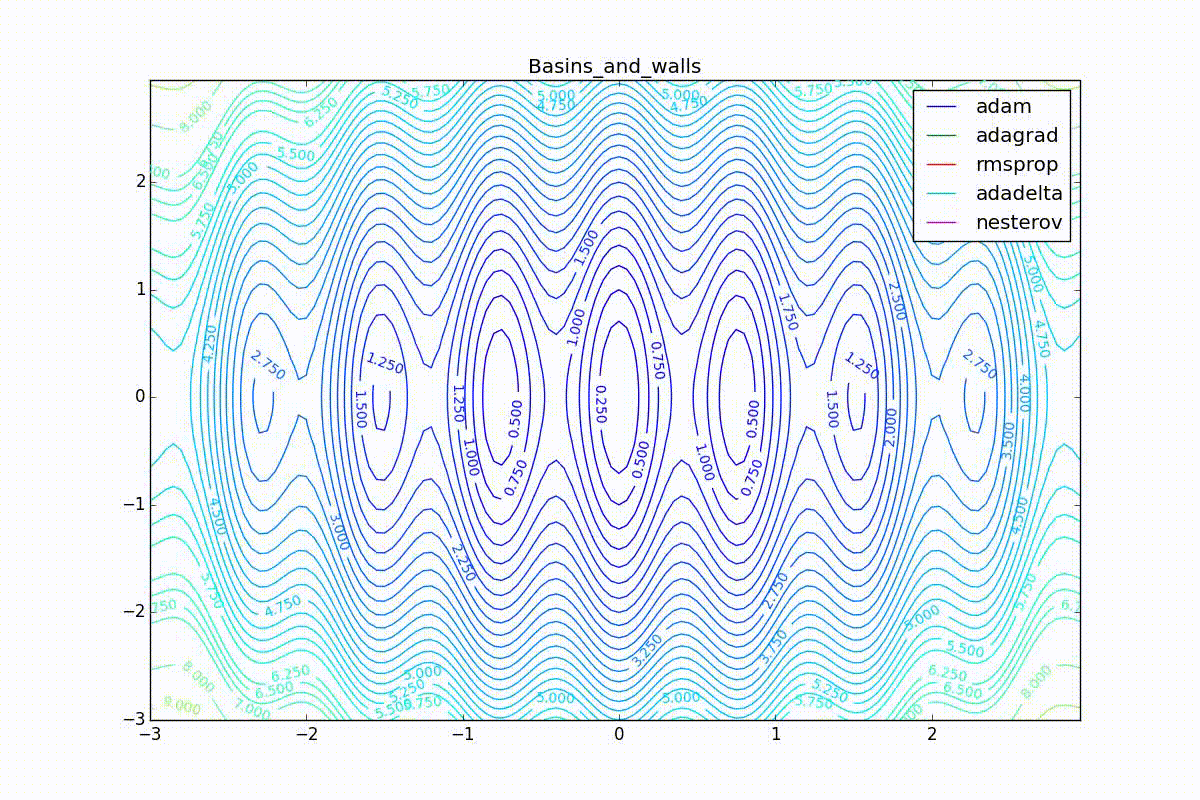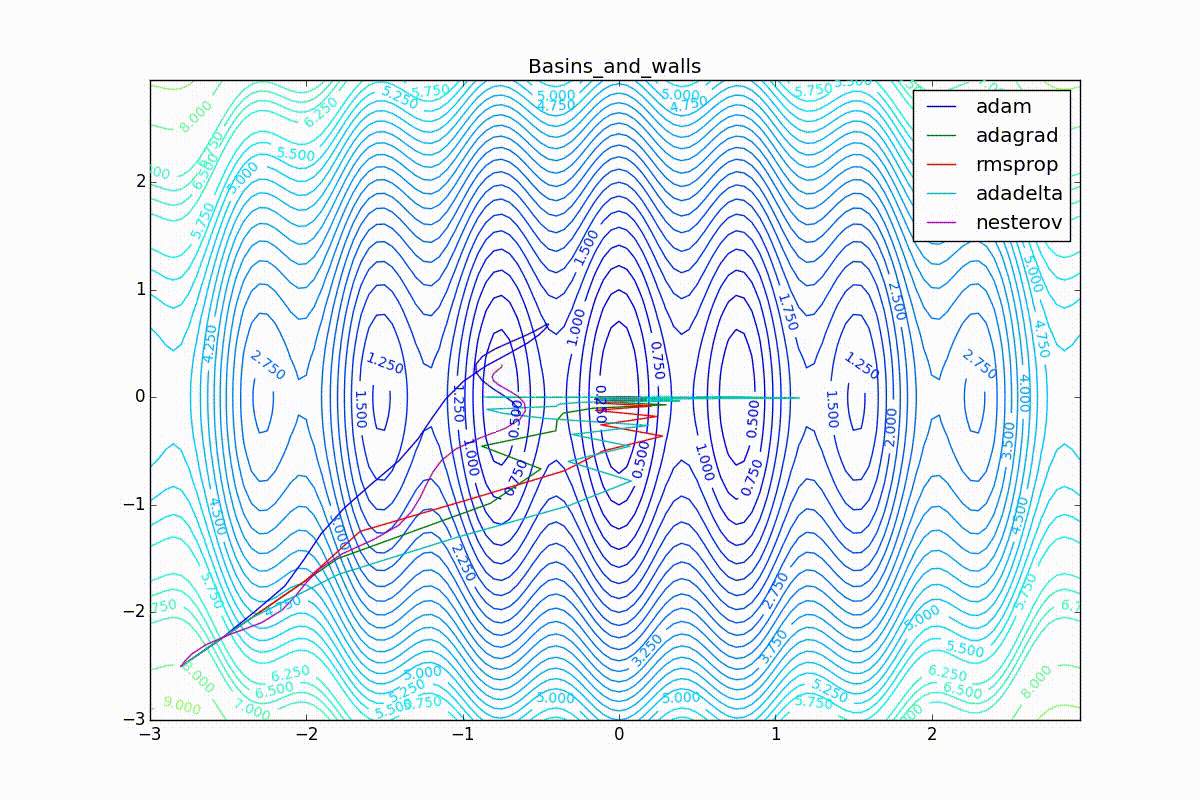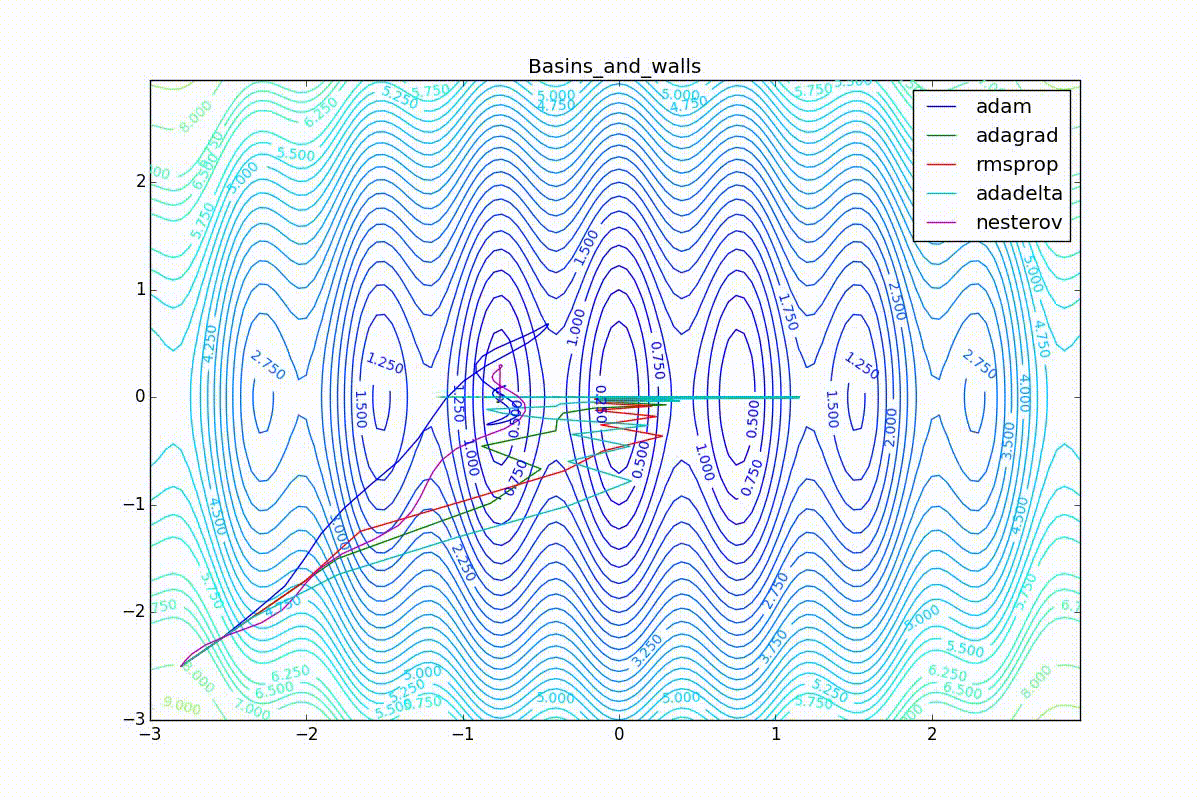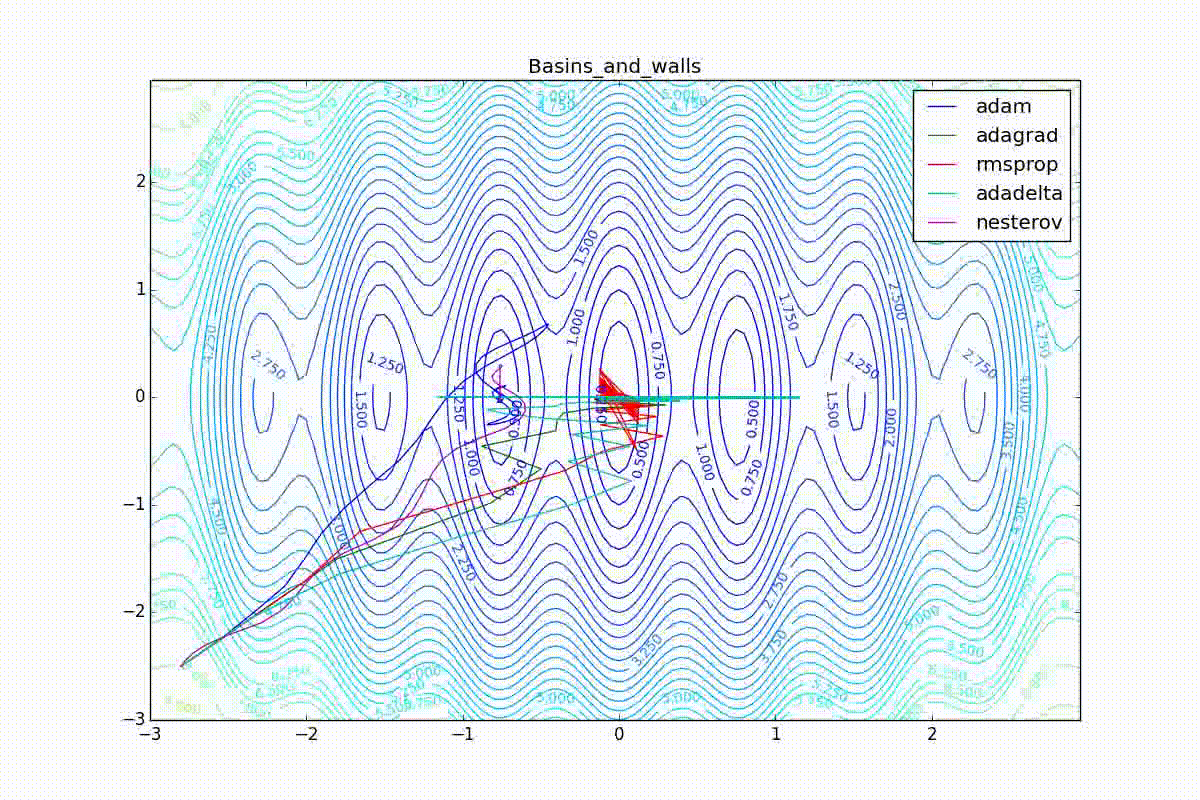
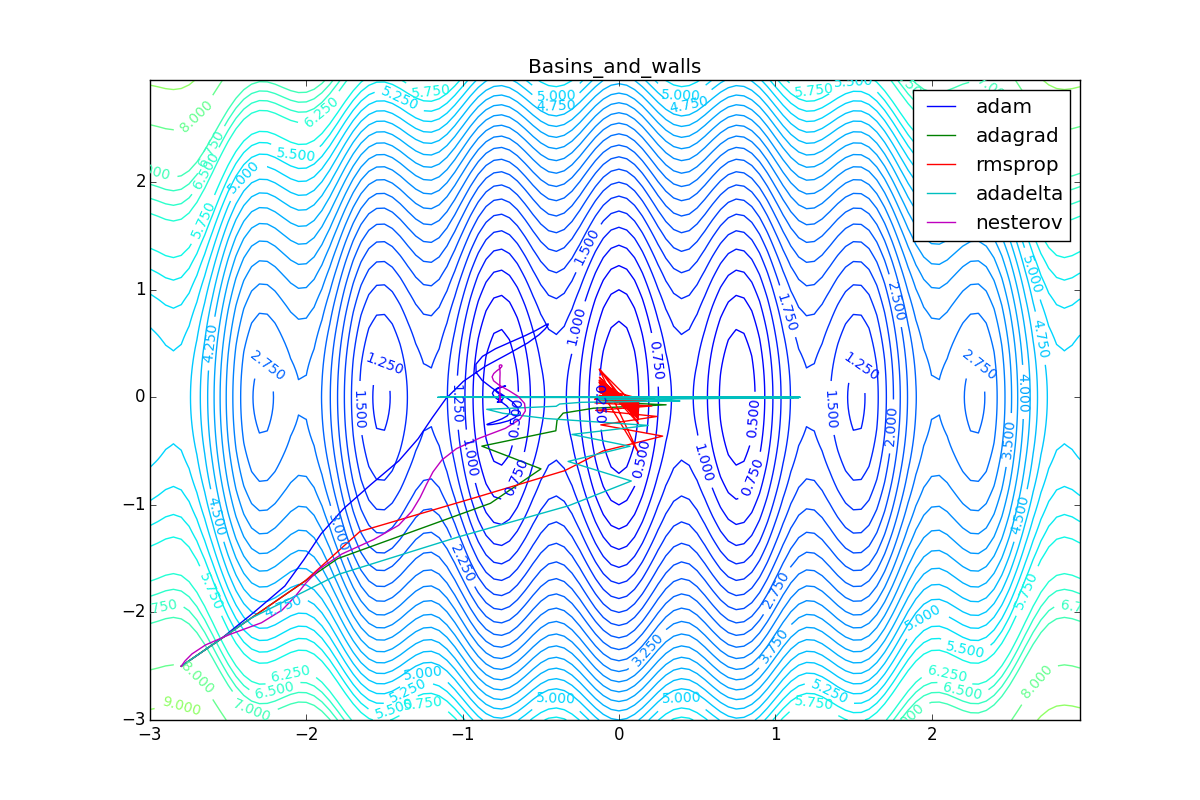
As you can see, they all converge quite well (with a minimum selection of the learning speed). Pay attention to what big steps Adam and RMSProp take at the beginning of training. This happens because from the very beginning there were no changes in any parameter (in any coordinate) and the sums in the denominators (14) and (23) are equal to zero. Here the situation is more complicated:
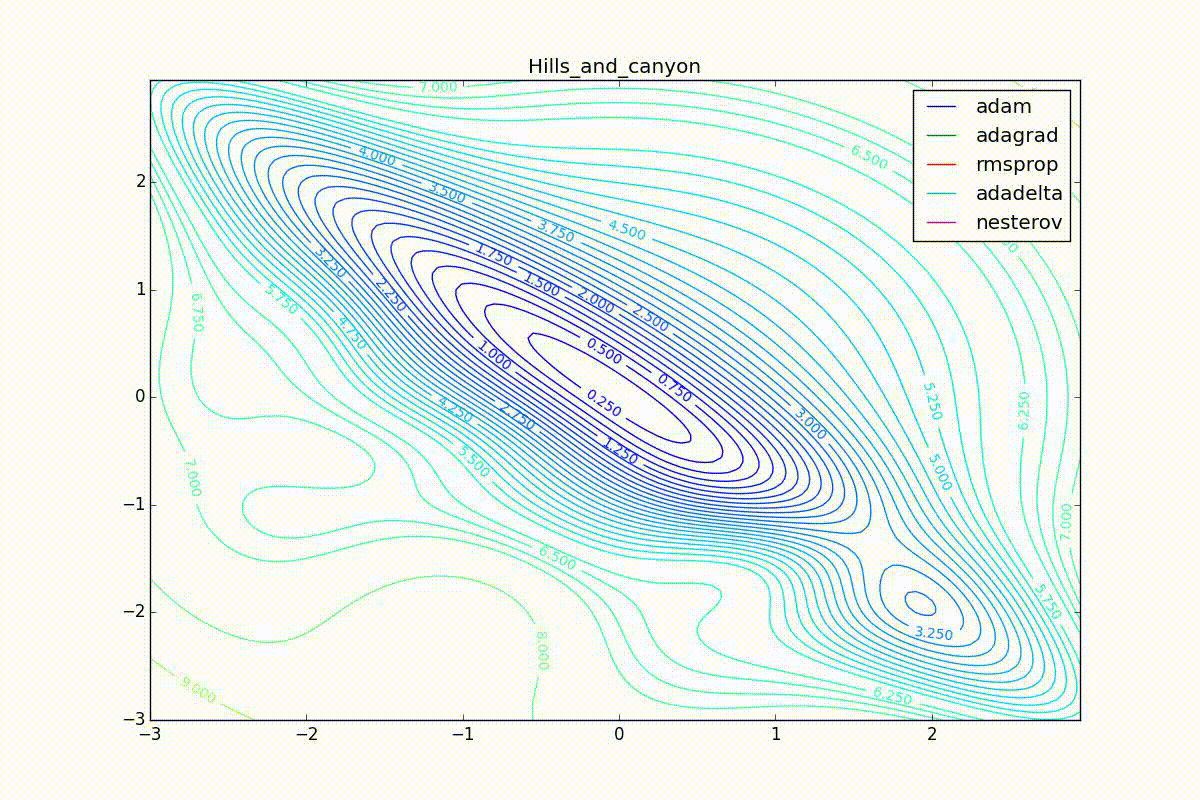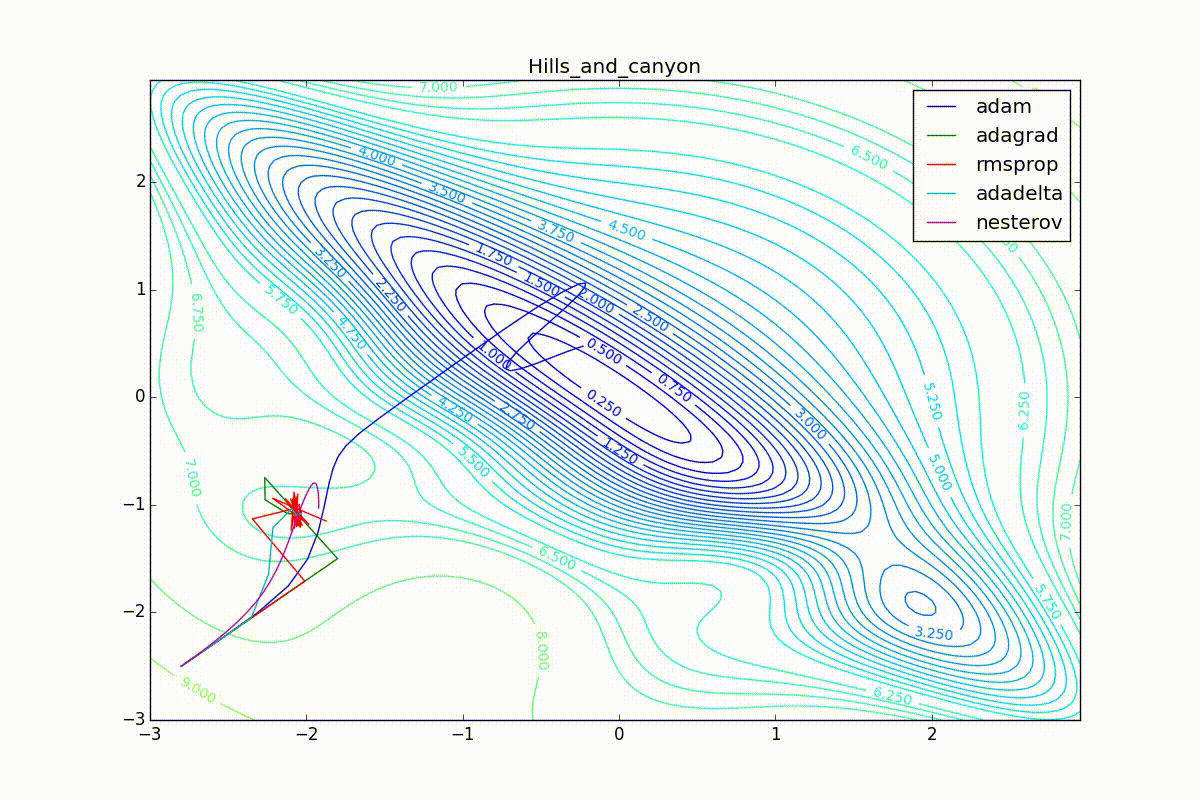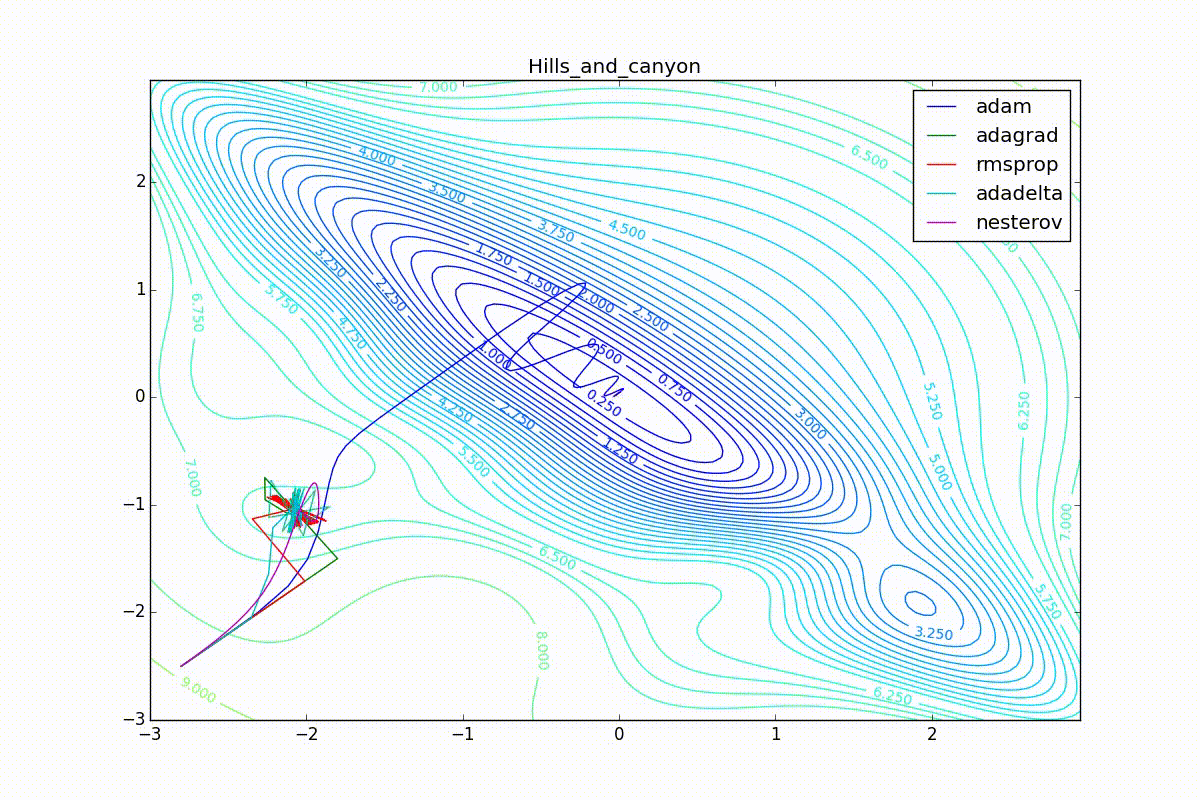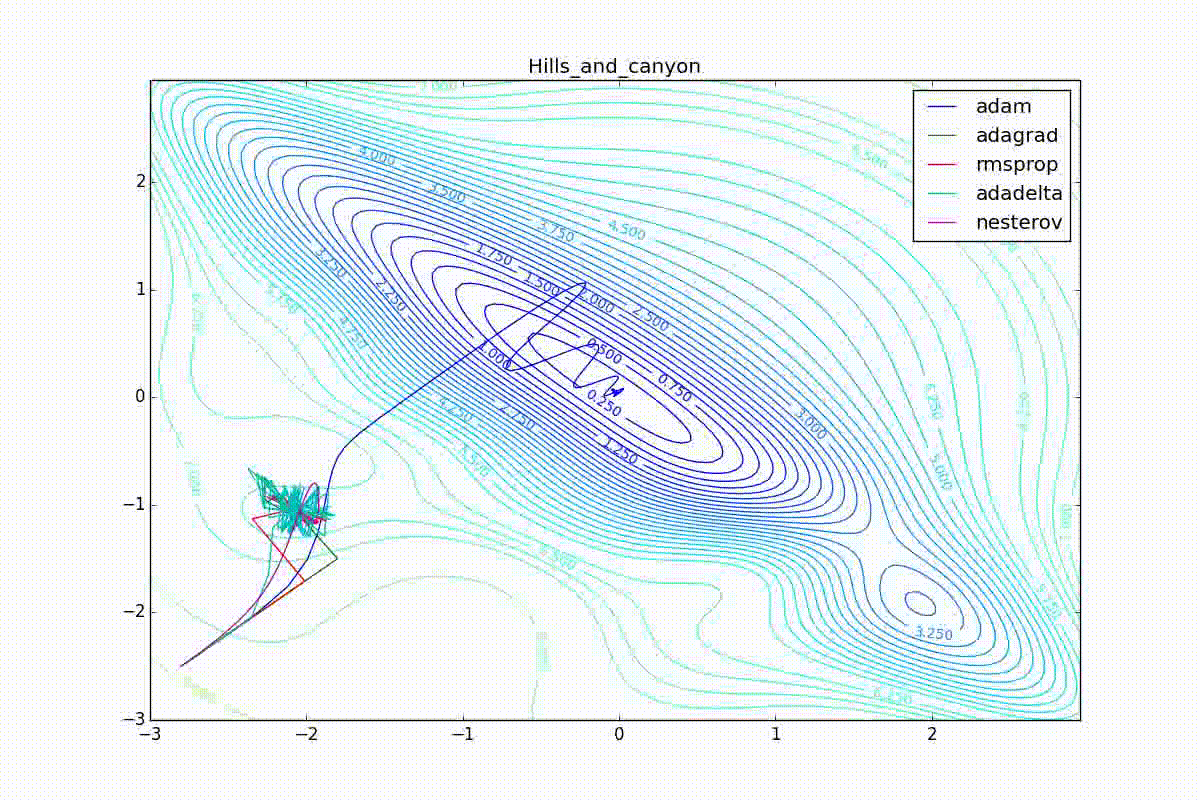
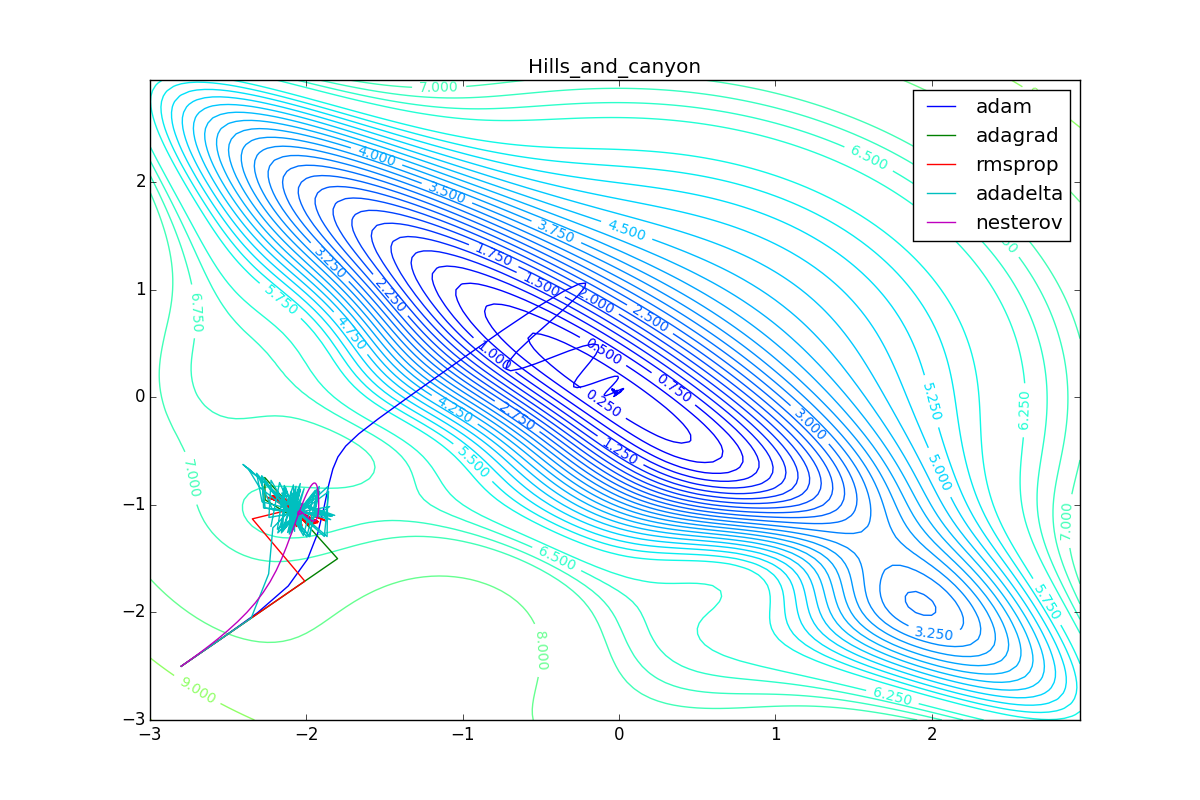
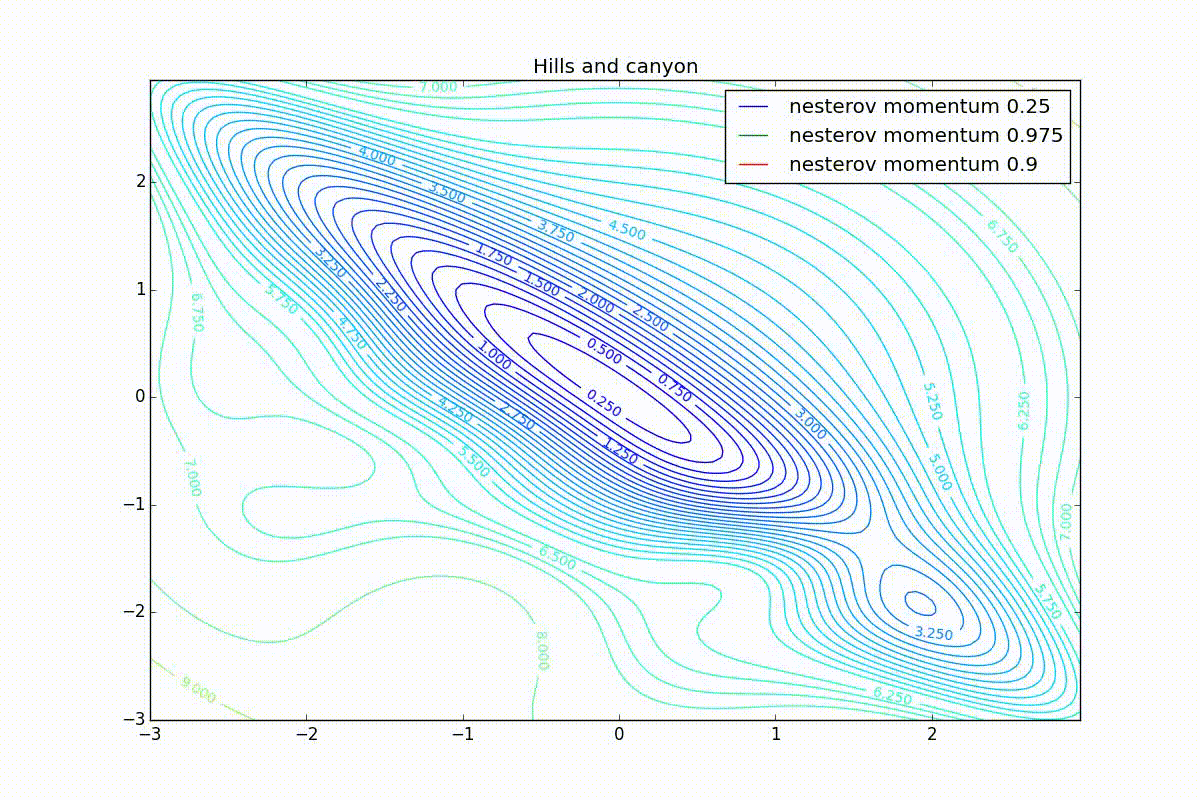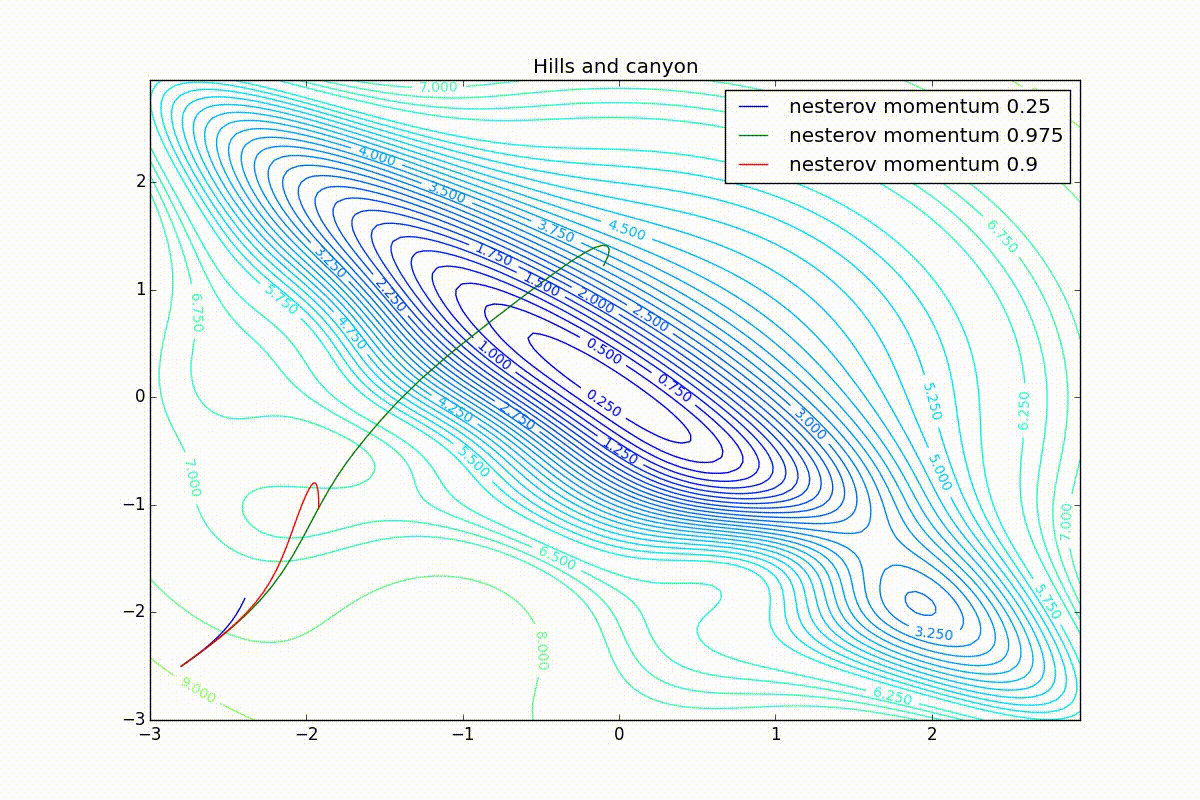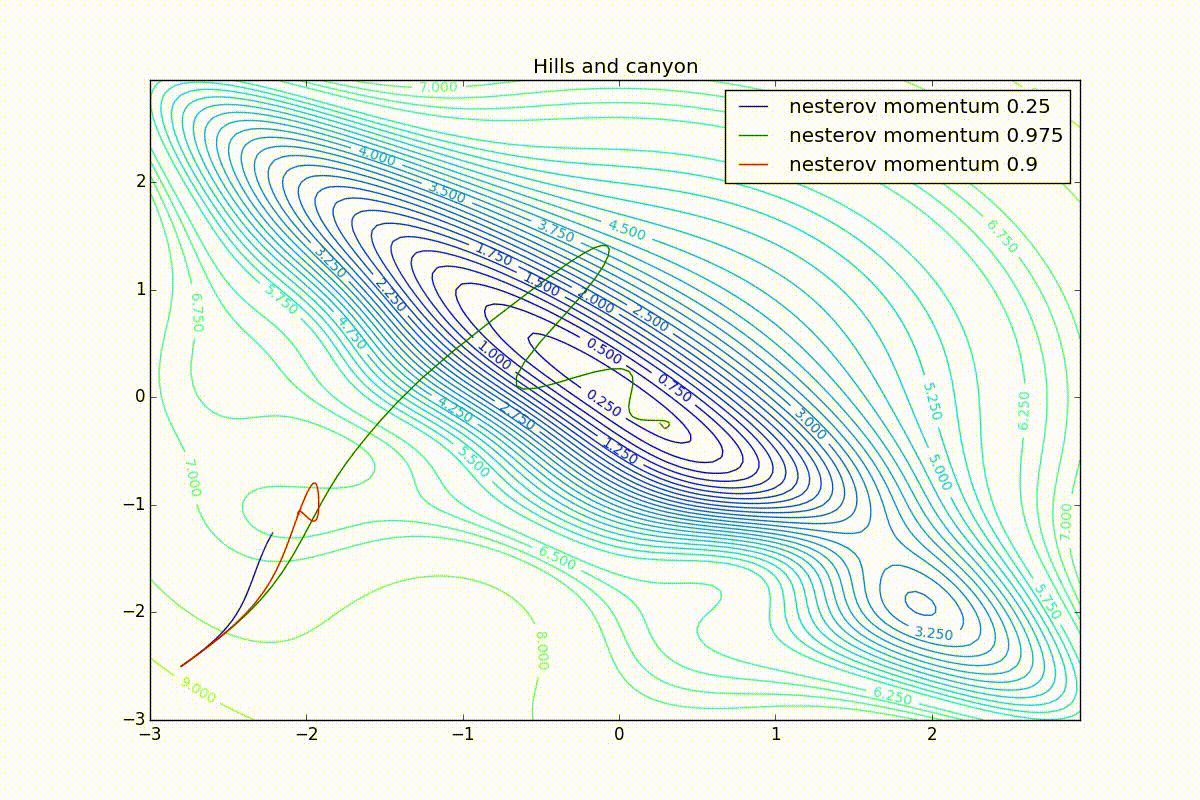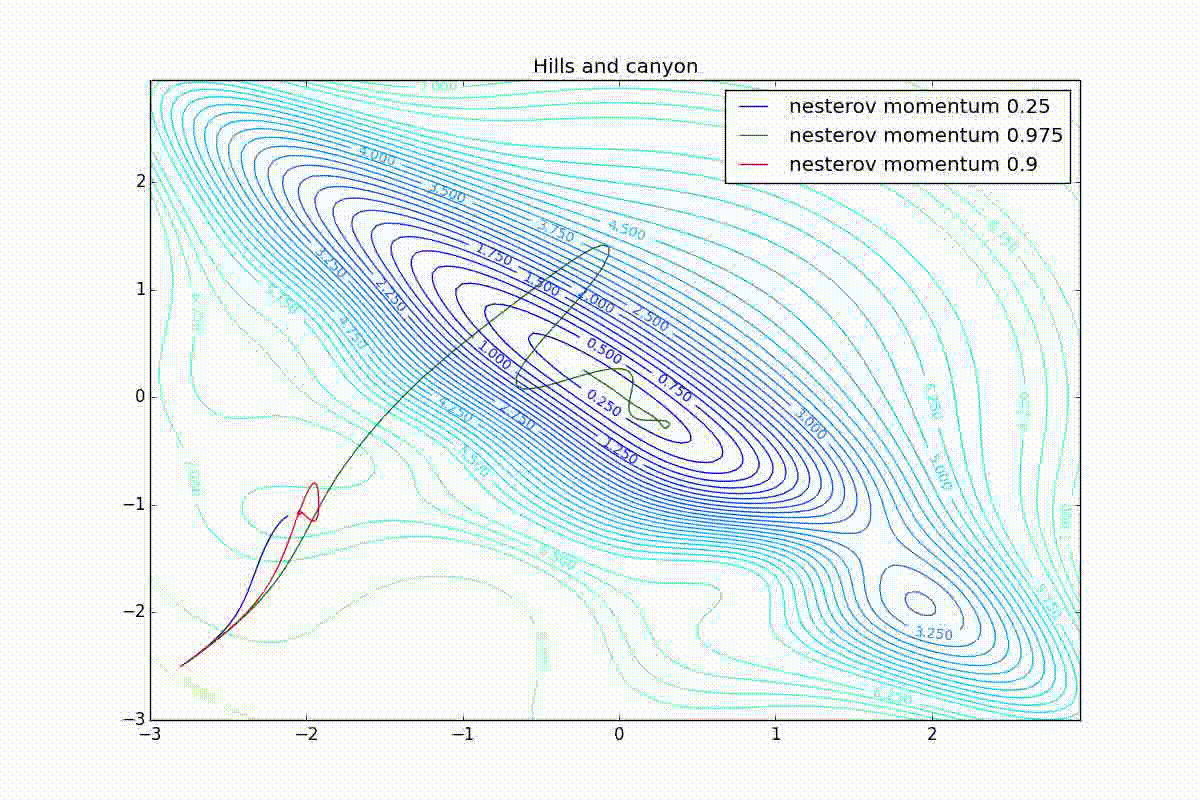
Apart from Adam, everyone was locked in a local minimum. Compare the behavior of the Nesterov method and, say, RMSProp in these graphs. Nesterov’s accelerated gradient, with any , falling into a local minimum, whirls around for a while, then loses momentum and decays at some point. RMSProp draws characteristic "hedgehogs". This is also related to the sum in the denominator (14) - in the trap, the gradient squares are small and the denominator becomes small again. The magnitude of the jumps is also affected, obviously, by the speed of training (the more
, the more jumps)
(the less, the more). Adagrad does not show this behavior, since this algorithm has a sum over the entire history of gradients, and not over the window. Usually this is a desirable behavior, it allows you to jump out of traps, but occasionally in this way the algorithm escapes from the global minimum, which again leads to an irreparable deterioration of the algorithm in the training set.
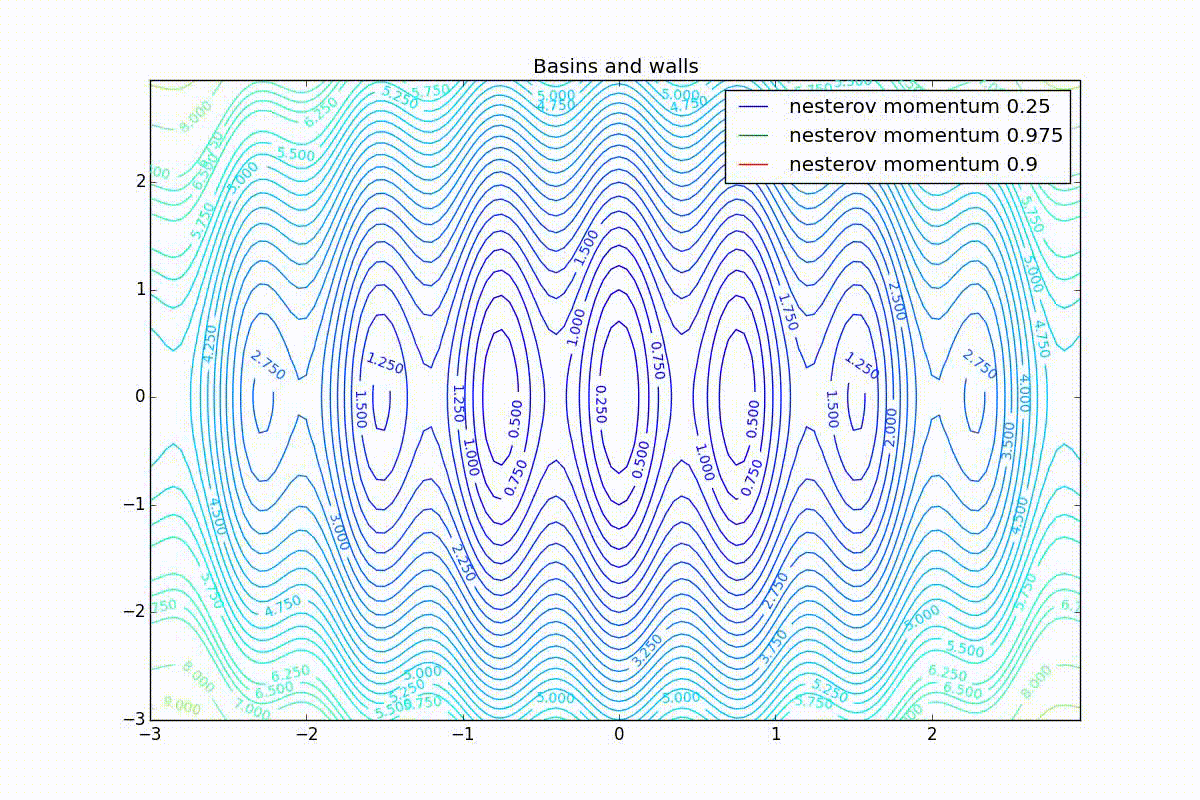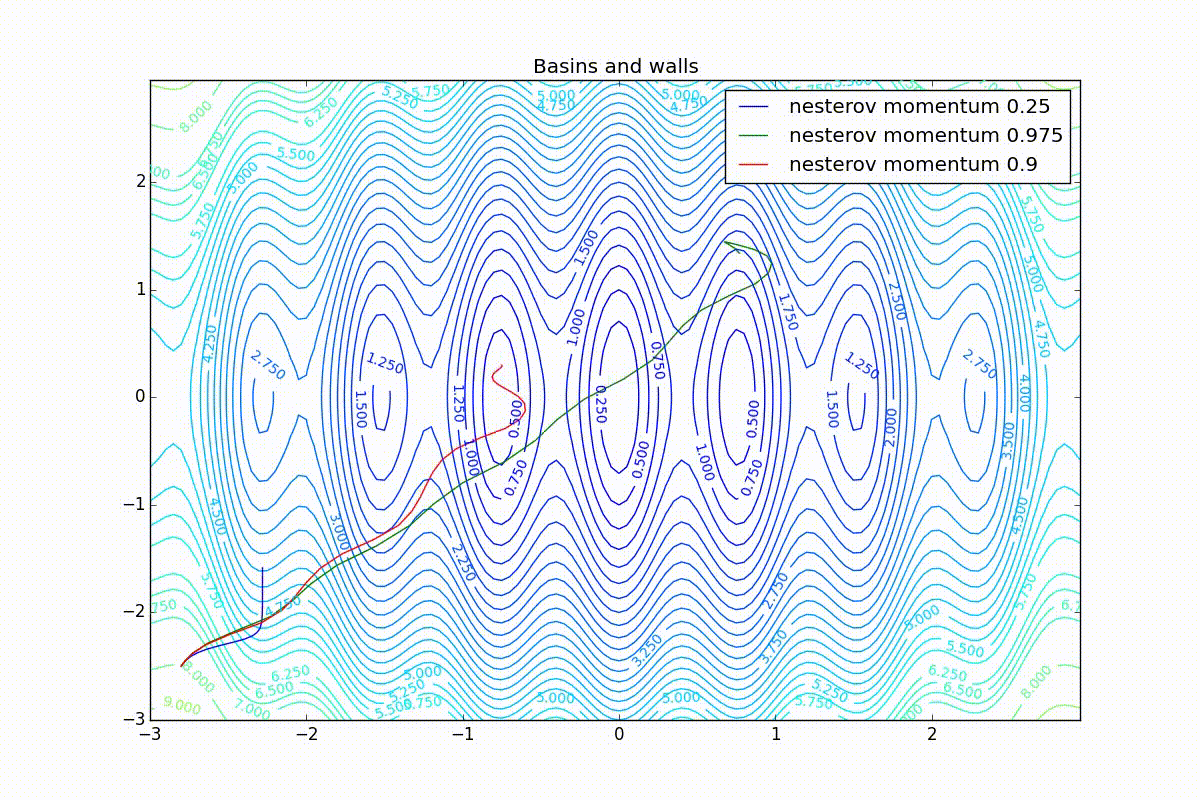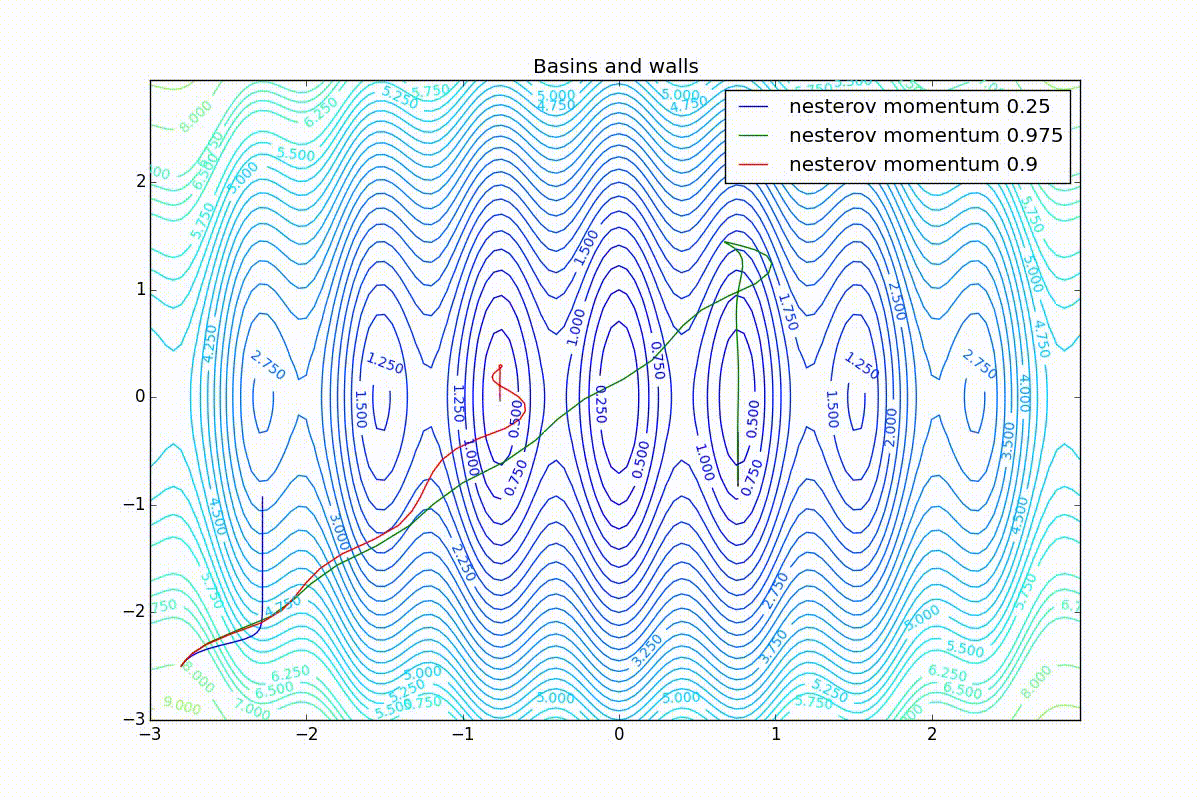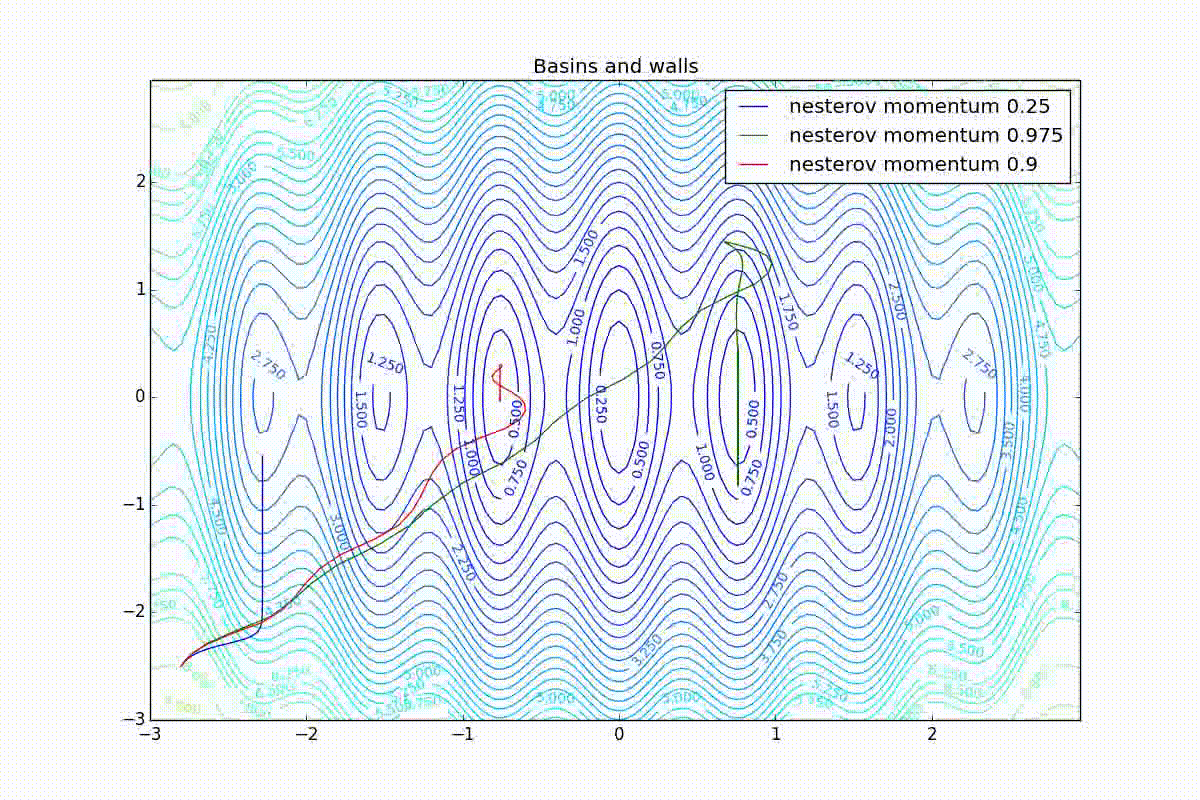
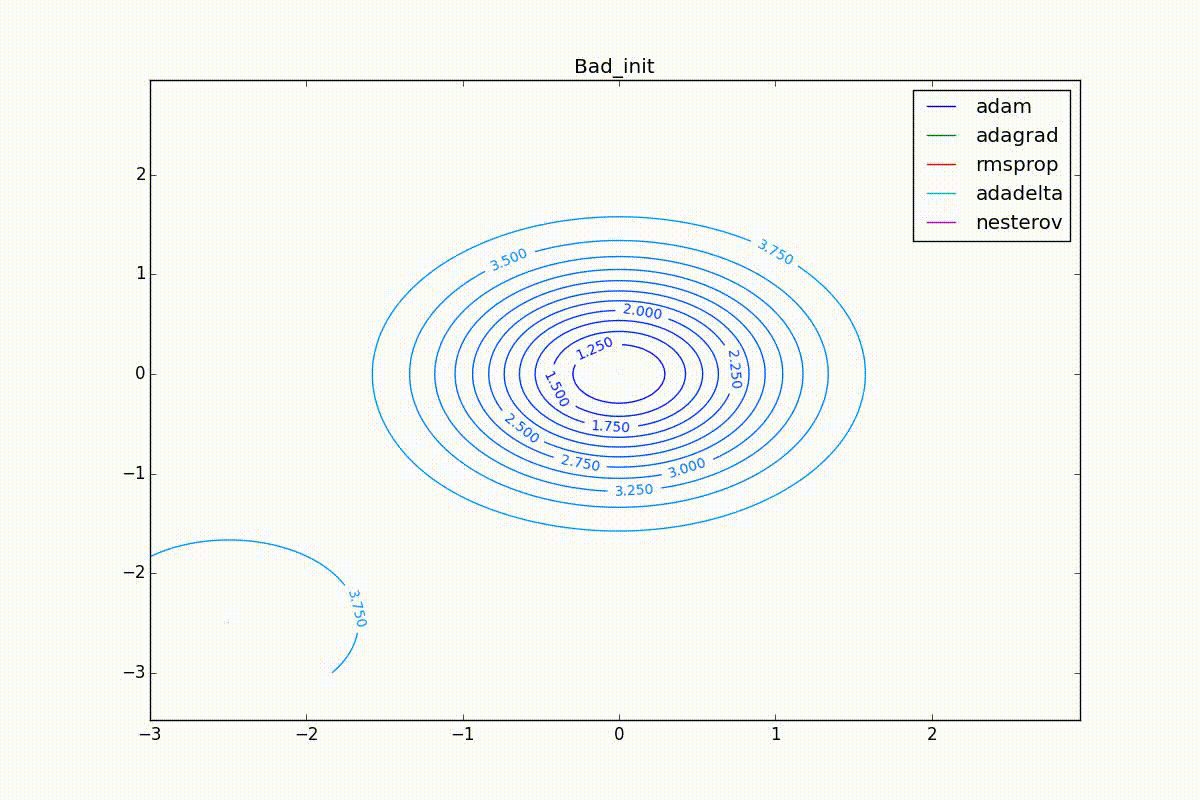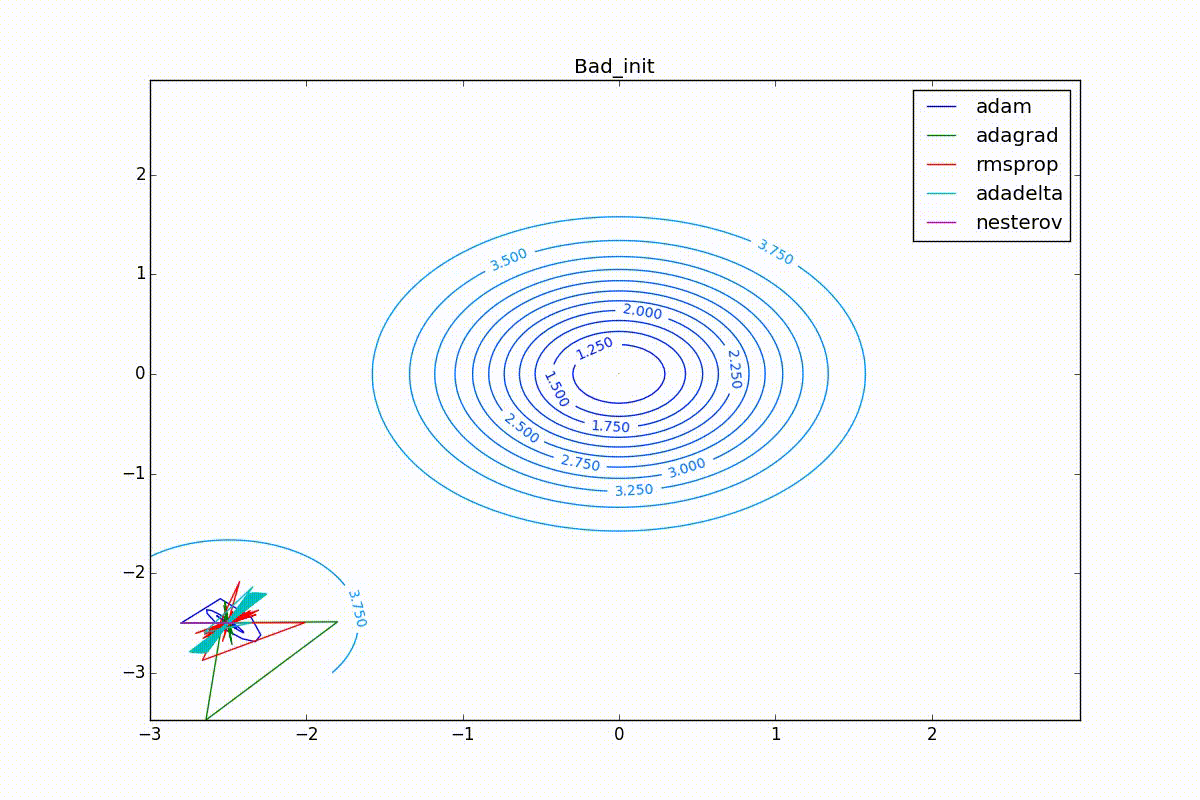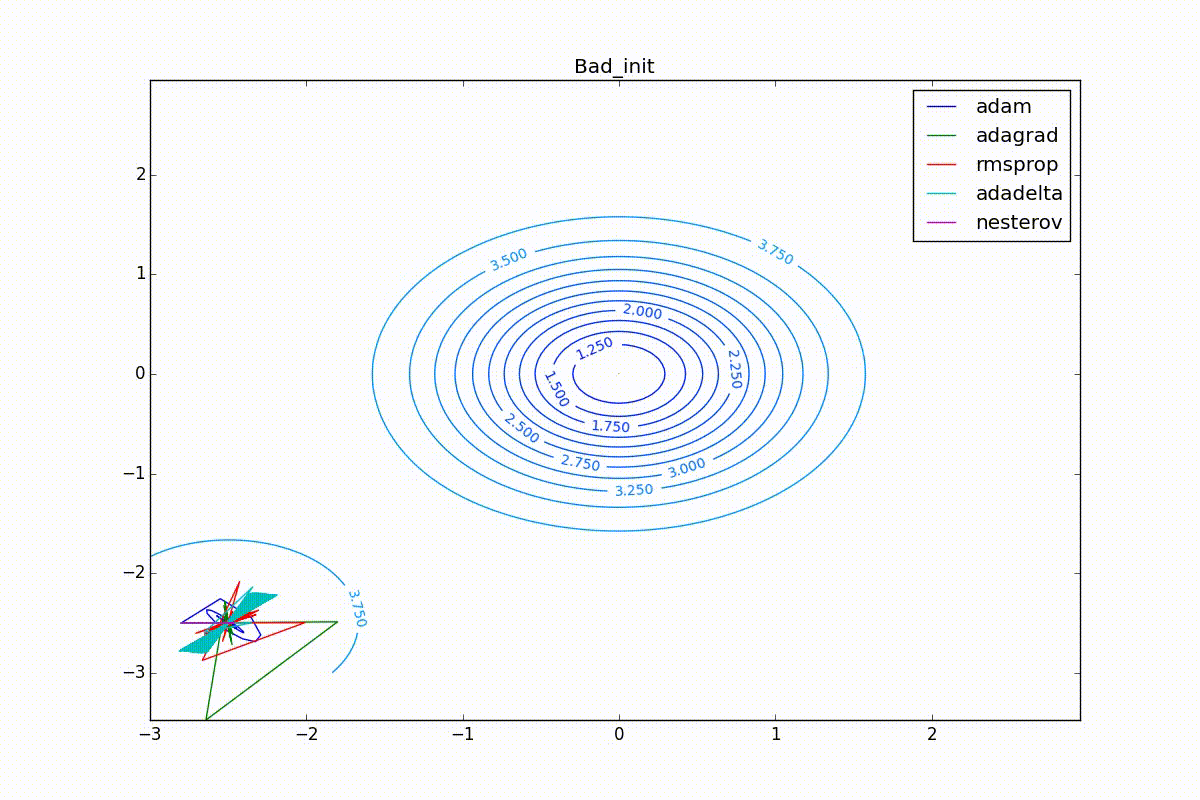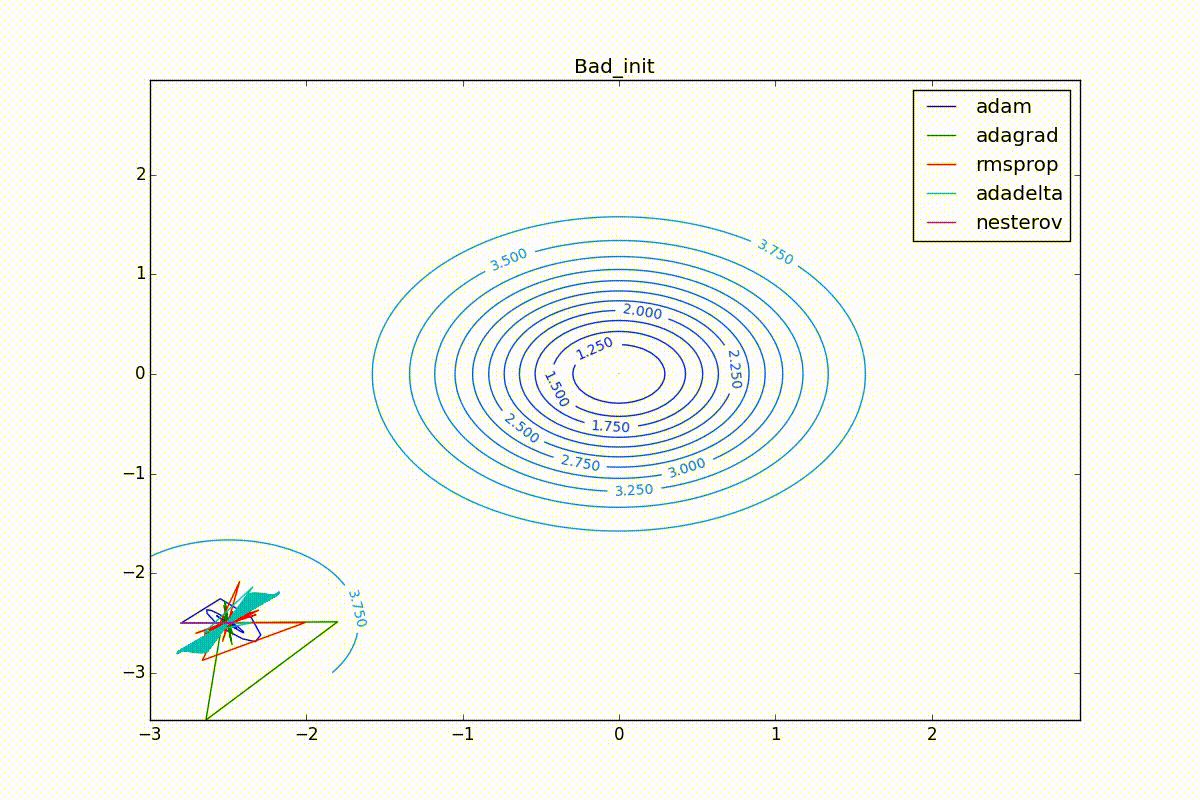
Finally, note that even though all these optimizers can find a way to a minimum even along a plateau with a very small slope or escape from a local minimum, if they have already gained momentum before, a bad starting point leaves them no chance:

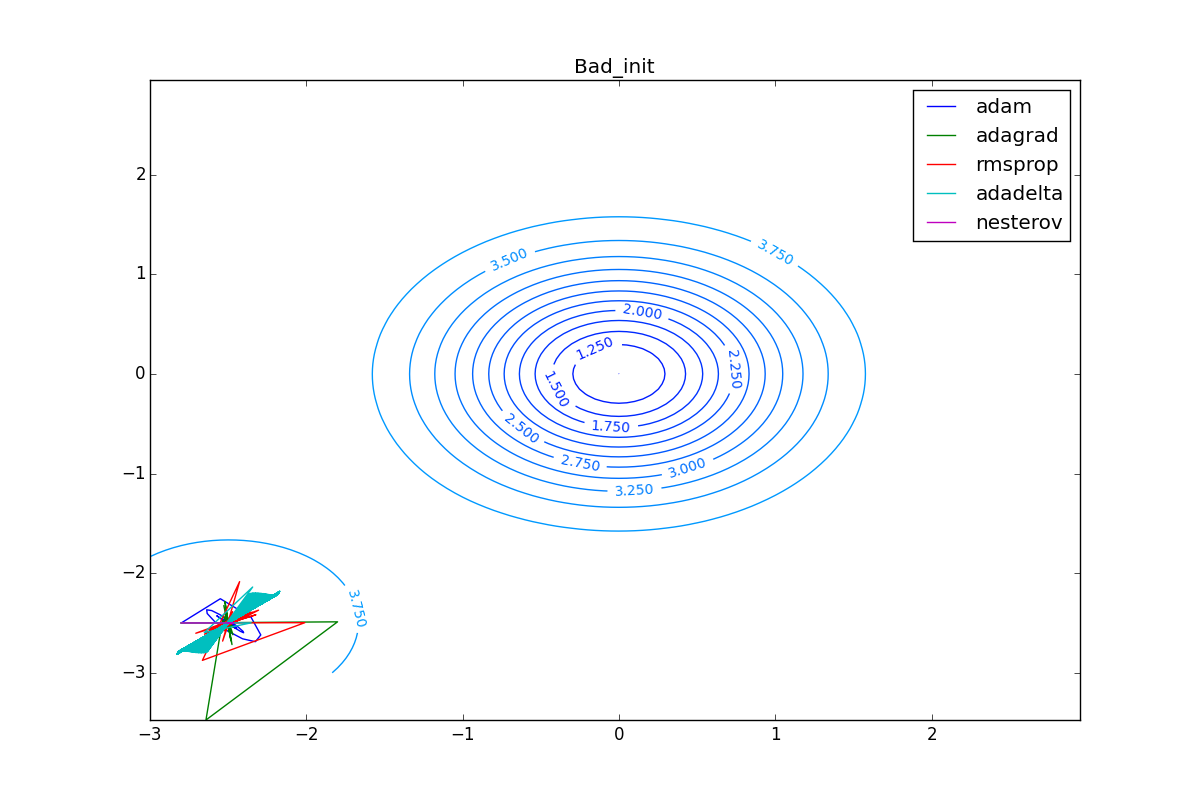
Conclusion
So, we examined some of the most popular first-order neural network optimizers. I hope these algorithms no longer seem like a magical black box with a bunch of mysterious parameters, and now you can make an informed decision about which of the optimizers to use in your tasks.
Finally, I’ll clarify one important point: it is unlikely that changing the algorithm for updating the scales with one swipe will solve all your problems with the neural network. Of course, the growth in the transition from SGD to something else will be obvious, but most likely the learning history for the algorithms described in the article, for relatively simple datasets and network structures, will look something like this:
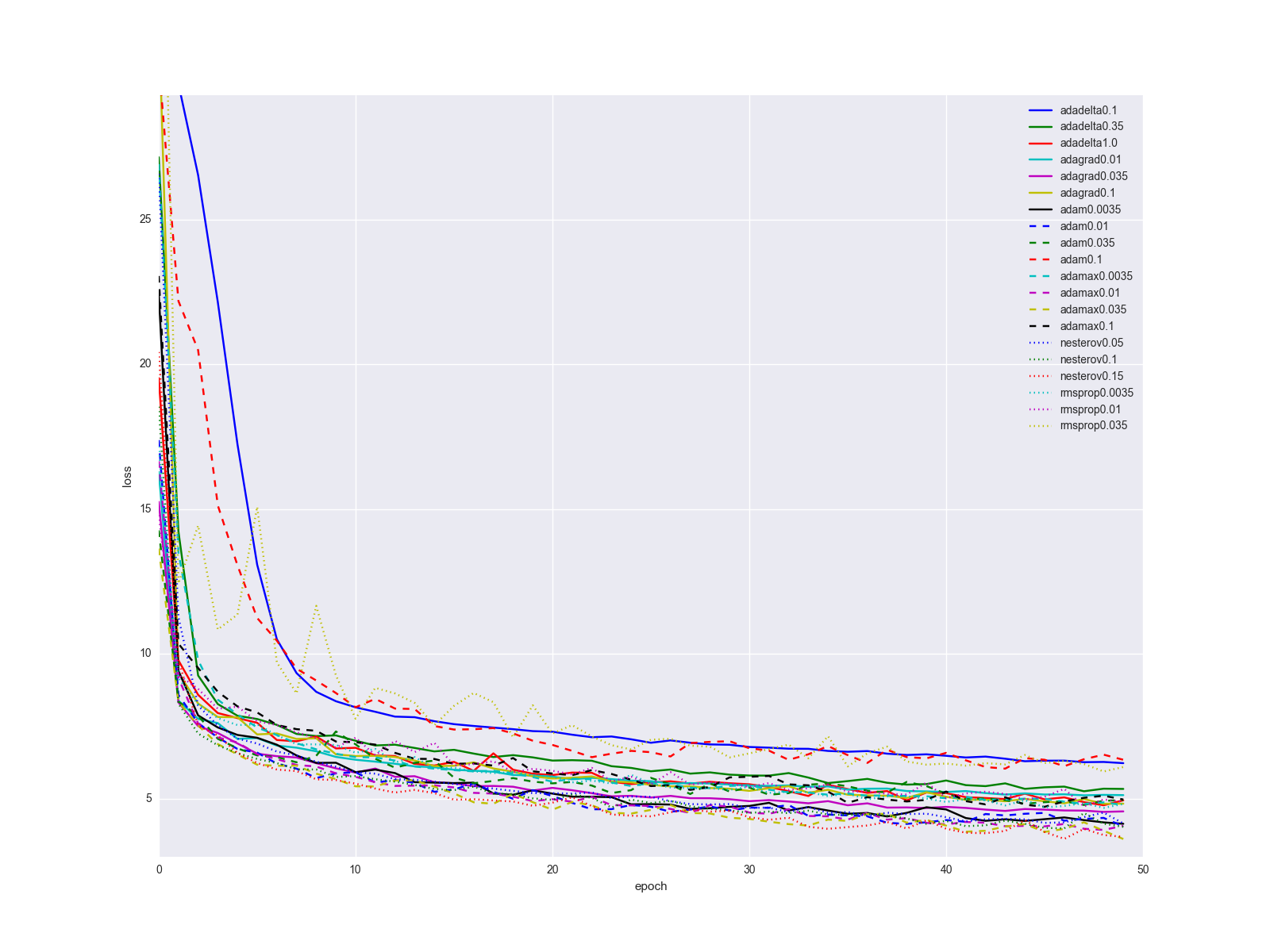
... not too impressive. I would suggest keeping Adam as the "golden hammer", as it gives the best results with minimal adjustment of parameters. When the network is already more or less debugged, try the Nesterov method with different parameters. Sometimes with it you can achieve better results, but it is relatively sensitive to changes in the network. Plus or minus a couple of layers and you need to look for a new optimal learning rate. Consider the rest of the algorithms and their parameters as a few more knobs and toggle switches that can be pulled in some special cases.
If you want some custom graphs with gradients, use this python script (requires python> 3.4, numpy and matplotlib):
from matplotlib import pyplot as plt
import numpy as np
from math import ceil, floor
deflinear_interpolation(X, idx):
idx_min = floor(idx)
idx_max = ceil(idx)
if idx_min == idx_max or idx_max >= len(X):
return X[idx_min]
elif idx_min < 0:
return X[idx_max]
else:
return X[idx_min] + (idx - idx_min)*X[idx_max]
defEDM(X, gamma, lr=0.25):
Y = []
v = 0for x in X:
v = gamma*v + lr*x
Y.append(v)
return np.asarray(Y)
defNM(X, gamma, lr=0.25):
Y = []
v = 0for i in range(len(X)):
v = gamma*v + lr*(linear_interpolation(X, i+gamma*v) if i+gamma*v < len(X) else0)
Y.append(v)
return np.asarray(Y)
defSmoothedNM(X, gamma, lr=0.25):
Y = []
v = 0for i in range(len(X)):
lookahead4 = linear_interpolation(X, i+gamma*v/4) if i+gamma*v/4 < len(X) else0
lookahead3 = linear_interpolation(X, i+gamma*v/2) if i+gamma*v/2 < len(X) else0
lookahead2 = linear_interpolation(X, i+gamma*v*3/4) if i+gamma*v*3/4 < len(X) else0
lookahead1 = linear_interpolation(X, i+gamma*v) if i+gamma*v < len(X) else0
v = gamma*v + lr*(lookahead4 + lookahead3 + lookahead2 + lookahead1)/4
Y.append(v)
return np.asarray(Y)
defAdagrad(X, eps, lr=2.5):
Y = []
G = 0for x in X:
G += x*x
v = lr/np.sqrt(G + eps)*x
Y.append(v)
return np.asarray(Y)
defRMSProp(X, gamma, lr=0.25, eps=0.00001):
Y = []
EG = 0for x in X:
EG = gamma*EG + (1-gamma)*x*x
v = lr/np.sqrt(EG + eps)*x
Y.append(v)
return np.asarray(Y)
defAdadelta(X, gamma, lr=50.0, eps=0.001):
Y = []
EG = 0
EDTheta = lr
for x in X:
EG = gamma*EG + (1-gamma)*x*x
v = np.sqrt(EDTheta + eps)/np.sqrt(EG + eps)*x
Y.append(v)
EDTheta = gamma*EDTheta + (1-gamma)*v*v
return np.asarray(Y)
defAdadeltaZeroStart(X, gamma, eps=0.001):return Adadelta(X, gamma, lr=0.0, eps=eps)
defAdadeltaBigStart(X, gamma, eps=0.001):return Adadelta(X, gamma, lr=50.0, eps=eps)
defAdam(X, beta1, beta2=0.999, lr=0.25, eps=0.0000001):
Y = []
m = 0
v = 0for i, x in enumerate(X):
m = beta1*m + (1-beta1)*x
v = beta2*v + (1-beta2)*x*x
m_hat = m/(1- pow(beta1, i+1) )
v_hat = v/(1- pow(beta2, i+1) )
dthetha = lr/np.sqrt(v_hat + eps)*m_hat
Y.append(dthetha)
return np.asarray(Y)
np.random.seed(413)
X = np.arange(0, 300)
D_Thetha_spikes = np.asarray( [int(x%60 == 0) for x in X])
D_Thetha_rectangles = np.asarray( [2*int(x%40 < 20) - 1for x in X])
D_Thetha_noisy_sin = np.asarray( [np.sin(x/20) + np.random.random() - 0.5for x in X])
D_Thetha_very_noisy_sin = np.asarray( [np.sin(x/20)/5 + np.random.random() - 0.5for x in X])
D_Thetha_uneven_sawtooth = np.asarray( [ x%20/(15*int(x > 80) + 5) for x in X])
D_Thetha_saturation = np.asarray( [ int(x % 80 < 40) for x in X])
for method_label, method, parameter_step in [
("GRAD_Simple_Momentum", EDM, [0.25, 0.9, 0.975]),
("GRAD_Nesterov", NM, [0.25, 0.9, 0.975]),
("GRAD_Smoothed_Nesterov", SmoothedNM, [0.25, 0.9, 0.975]),
("GRAD_Adagrad", Adagrad, [0.0000001, 0.1, 10.0]),
("GRAD_RMSProp", RMSProp, [0.25, 0.9, 0.975]),
("GRAD_AdadeltaZeroStart", AdadeltaZeroStart, [0.25, 0.9, 0.975]),
("GRAD_AdadeltaBigStart", AdadeltaBigStart, [0.25, 0.9, 0.975]),
("GRAD_Adam", Adam, [0.25, 0.9, 0.975]),
]:
for label, D_Thetha in [("spikes", D_Thetha_spikes),
("rectangles", D_Thetha_rectangles),
("noisy sin", D_Thetha_noisy_sin),
("very noisy sin", D_Thetha_very_noisy_sin),
("uneven sawtooth", D_Thetha_uneven_sawtooth),
("saturation", D_Thetha_saturation), ]:
fig = plt.figure(figsize=[16.0, 9.0])
ax = fig.add_subplot(111)
ax.plot(X, D_Thetha, label="gradient")
for gamma in parameter_step:
Y = method(D_Thetha, gamma)
ax.plot(X, Y, label="param="+str(gamma))
ax.spines['bottom'].set_position('zero')
full_name = method_label + "_" + label
plt.xticks(np.arange(0, 300, 20))
plt.grid(True)
plt.title(full_name)
plt.xlabel('epoch')
plt.ylabel('value')
plt.legend()
# plt.show(block=True) #Uncoomment and comment next line if you just want to watch
plt.savefig(full_name)
plt.close(fig)If you want to experiment with algorithm parameters and your own functions, use this to create your own minimizer trajectory animation (theano / lasagne is also required):
import numpy as np
import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import theano
import theano.tensor as T
from lasagne.updates import nesterov_momentum, rmsprop, adadelta, adagrad, adam
#For reproducibility. Comment it out for randomness
np.random.seed(413)
#Uncoomment and comment next line if you want to try random init# clean_random_weights = scipy.random.standard_normal((2, 1))
clean_random_weights = np.asarray([[-2.8], [-2.5]])
W = theano.shared(clean_random_weights)
Wprobe = T.matrix('weights')
levels = [x/4.0for x in range(-8, 2*12, 1)] + [6.25, 6.5, 6.75, 7] + \
list(range(8, 20, 1))
levels = np.asarray(levels)
O_simple_quad = (W**2).sum()
O_wobbly = (W**2).sum()/3 + T.abs_(W[0][0])*T.sqrt(T.abs_(W[0][0]) + 0.1) + 3*T.sin(W.sum()) + 3.0 + 8*T.exp(-2*((W[0][0] + 1)**2+(W[1][0] + 2)**2))
O_basins_and_walls = (W**2).sum()/2 + T.sin(W[0][0]*4)**2
O_ripple = (W**2).sum()/3 + (T.sin(W[0][0]*20)**2 + T.sin(W[1][0]*20)**2)/15
O_giant_plateu = 4*(1-T.exp(-((W[0][0])**2+(W[1][0])**2)))
O_hills_and_canyon = (W**2).sum()/3 + \
3*T.exp(-((W[0][0] + 1)**2+(W[1][0] + 2)**2)) + \
T.exp(-1.5*(2*(W[0][0] + 2)**2+(W[1][0] -0.5)**2)) + \
3*T.exp(-1.5*((W[0][0] -1)**2+2*(W[1][0] + 1.5)**2)) + \
1.5*T.exp(-((W[0][0] + 1.5)**2+3*(W[1][0] + 0.5)**2)) + \
4*(1 - T.exp(-((W[0][0] + W[1][0])**2)))
O_two_minimums = 4-0.5*T.exp(-((W[0][0] + 2.5)**2+(W[1][0] + 2.5)**2))-3*T.exp(-((W[0][0])**2+(W[1][0])**2))
nesterov_testsuit = [
(nesterov_momentum, "nesterov momentum 0.25", {"learning_rate": 0.01, "momentum": 0.25}),
(nesterov_momentum, "nesterov momentum 0.9", {"learning_rate": 0.01, "momentum": 0.9}),
(nesterov_momentum, "nesterov momentum 0.975", {"learning_rate": 0.01, "momentum": 0.975})
]
cross_method_testsuit = [
(nesterov_momentum, "nesterov", {"learning_rate": 0.01}),
(rmsprop, "rmsprop", {"learning_rate": 0.25}),
(adadelta, "adadelta", {"learning_rate": 100.0}),
(adagrad, "adagrad", {"learning_rate": 1.0}),
(adam, "adam", {"learning_rate": 0.25})
]
for O, plot_label in [
(O_wobbly, "Wobbly"),
(O_basins_and_walls, "Basins_and_walls"),
(O_giant_plateu, "Giant_plateu"),
(O_hills_and_canyon, "Hills_and_canyon"),
(O_two_minimums, "Bad_init")
]:
result_probe = theano.function([Wprobe], O, givens=[(W, Wprobe)])
history = {}
for method, history_mark, kwargs_to_method in cross_method_testsuit:
W.set_value(clean_random_weights)
history[history_mark] = [W.eval().flatten()]
updates = method(O, [W], **kwargs_to_method)
train_fnc = theano.function(inputs=[], outputs=O, updates=updates)
for i in range(125):
result_val = train_fnc()
print("Iteration " + str(i) + " result: "+ str(result_val))
history[history_mark].append(W.eval().flatten())
print("-------- DONE {}-------".format(history_mark))
delta = 0.05
mesh = np.arange(-3.0, 3.0, delta)
X, Y = np.meshgrid(mesh, mesh)
Z = []
for y in mesh:
z = []
for x in mesh:
z.append(result_probe([[x], [y]]))
Z.append(z)
Z = np.asarray(Z)
print("-------- BUILT MESH -------")
fig, ax = plt.subplots(figsize=[12.0, 8.0])
CS = ax.contour(X, Y, Z, levels=levels)
plt.clabel(CS, inline=1, fontsize=10)
plt.title(plot_label)
nphistory = []
for key in history:
nphistory.append(
[np.asarray([h[0] for h in history[key]]),
np.asarray([h[1] for h in history[key]]),
key]
)
lines = []
for nph in nphistory:
lines += ax.plot(nph[0], nph[1], label=nph[2])
leg = plt.legend()
plt.savefig(plot_label + '_final.png')
defanimate(i):for line, hist in zip(lines, nphistory):
line.set_xdata(hist[0][:i])
line.set_ydata(hist[1][:i])
return lines
definit():for line, hist in zip(lines, nphistory):
line.set_ydata(np.ma.array(hist[0], mask=True))
return lines
ani = animation.FuncAnimation(fig, animate, np.arange(1, 120), init_func=init,
interval=100, repeat_delay=0, blit=True, repeat=True)
print("-------- WRITING ANIMATION -------")
# plt.show(block=True) #Uncoomment and comment next line if you just want to watch
ani.save(plot_label + '.mp4', writer='ffmpeg_file', fps=5)
print("-------- DONE {} -------".format(plot_label))Thanks to Roman Parpalak for the tool , thanks to which working with formulas on the Habré is not so painful. You can see the article that I took as the basis of my article - there is a lot of useful information that I omitted in order to better focus on optimization algorithms. To further delve deeper into neural networks, I recommend this book.
Have a nice New Year's weekend, Habr!
