Formulation of the problem

This is the second, final article. I recall the goal: there is a DC motor. The task is to develop, assemble and test a device that allows you to implement a control loop with a current setting in relation to this engine. The desired transient time on a stalled engine (without counter-EMF) is not more than 10ms.

The text is divided into two articles:

• 1. Measurement of resistance and inductance of the motor
• 2. Development of the control circuit

I remind you what the layout of the control iron looks like:

Desired Result

The whole system is like a black box

So, the whole idea is that I want to directly set the strength of the current flowing through my engine. If you combine the controller and engine together, then I would like to get something like the following:


Here J (t) is the current reference, I (t) is the current flowing through the motor. I would like the input and output signals to be connected according to the law τ I '(t) + I (t) = J (t) . This law is chosen arbitrarily, I just like this differential equation. In clever words, it is called an aperiodic link of the first order. Controllers that obey this law even have their own symbol on some circuits:

Here is the reaction of such a link to a single step effect:


This is a beautiful exponential convergence without various vibrations, which is why this form was chosen. The constant tau in the formula τ I '(t) + I (t) = J (t) is called the time constant, this is the time during which the process will reach 63% of its final value when reacting to a single jump. If we define the time of the transition process as the time to reach 98% of the final value, then this is approximately 5 tau. In the statement of the problem, the transition process time should not exceed 10ms, so we take τ = 0.002 .

Slightly open the black box

If you open the black box, it will look something like this:

At the input of the black box, we give a signal J (t), at the output we get the flowing current I (t). Inside the black box there are two elevators: an engine with its own diffuser, connecting the voltage at the terminals U (t) with the current I (t) flowing through it, and the regulator itself, which must supply voltage U (t) depending on the current J (t) and really flowing current I (t).

Let's say that the regulator takes the input error E (t) - this is the difference between the desired current and the real one, and the output gives the voltage U (t). Our task is to find the diffusion that connects E (t) and U (t), then it will be clear how to program the controller arduino.

So, we want the current task and the real current to be related according to the law we have chosen:


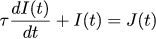
We apply the Laplace transform (with zero initial values) to it:


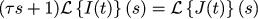
And make the following proportion:


Just in case, in control theory this proportion is called the transfer function.

We define the error E (t) as the difference between the desired and real current strength:


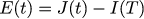
To adjust the current loop, we fix the motor shaft, thus the angular velocity leaves the motor diffuser:


In the previous article, we deduced the relationship between the voltage at the motor terminals and the strength of the flowing current (with the rotor fixed):


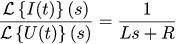
Let's divide this proportion into the proportion from equation (1):


Almost done, it remains to move from the Laplace coordinates to the usual temporary. To begin with, we will reveal the proportion:


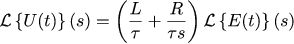
Armed with Laplace transform tables , you can see the following:


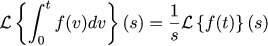
And this means that the voltage U (t) and the error of the task E (t) must be connected according to the following law:


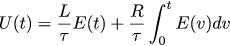
Thus, choosing the behavior of the entire system as an aperiodic first-order unit, we get that the necessary regulator is nothing but a regular PI regulator.

Realization

The controller code can be viewed here. The program is quite standard, the only thing to note is that the atmega lacks the health to work with floating points. Therefore, all work is done with a fixed point and integer variables.

Checking the operation of the regulator

To check the operation of the regulator, we will assign a meander and a sinusoidal signal to its input.

Meander

Here you can take the experimental data: from the zero initial state, we set the desired current strength at I0 = 4A and measure the actually flowing current.

Then let's calculate on paper, according to what law the flowing current should change under such conditions. This one-to-one coincides with what we did in the previous article:


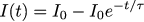
Let’s try to choose the parameter value so that the theoretical curve best approximates the real data and compares it with the time constant chosen by us earlier. Parameter selection code can be found here.

Here is the result of the control loop working on the meander half-cycle:


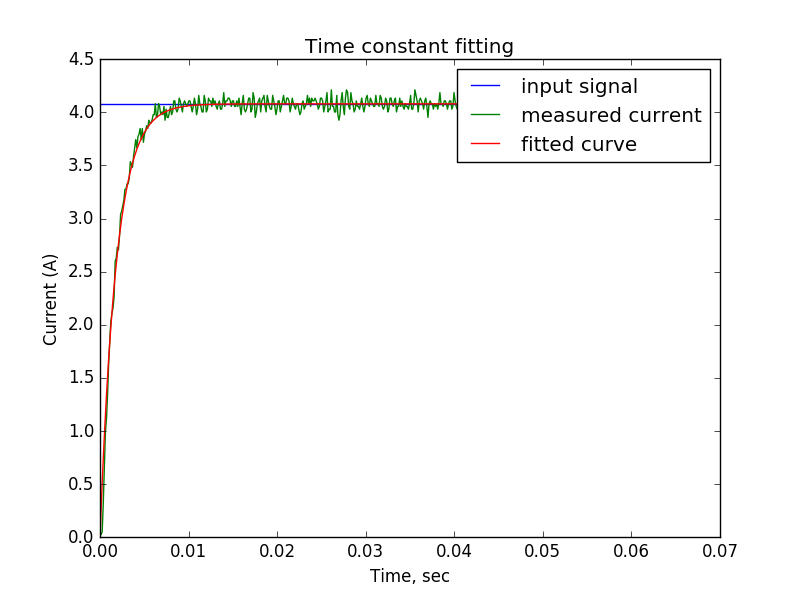
The least squares method tells us that the best value for the parameter is .00184, which is very close to the time constant .002 that we have chosen. It is clearly seen that the transition process was within ten milliseconds, which were allotted to him in the formulation of the problem.

Sine wave

Just in case, the second check, again, the calculations are all taken from the previous article. With a sinusoidal reference, the current strength I (t) should change according to the following law:


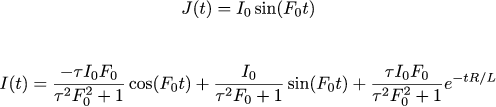
The code for selecting the parameter of the theoretical curve can be taken here. He tells us that the time constant is .00196, which again is close to the calculated parameter of 2ms.

Here is the result of the control loop working on a sinusoidal input signal:

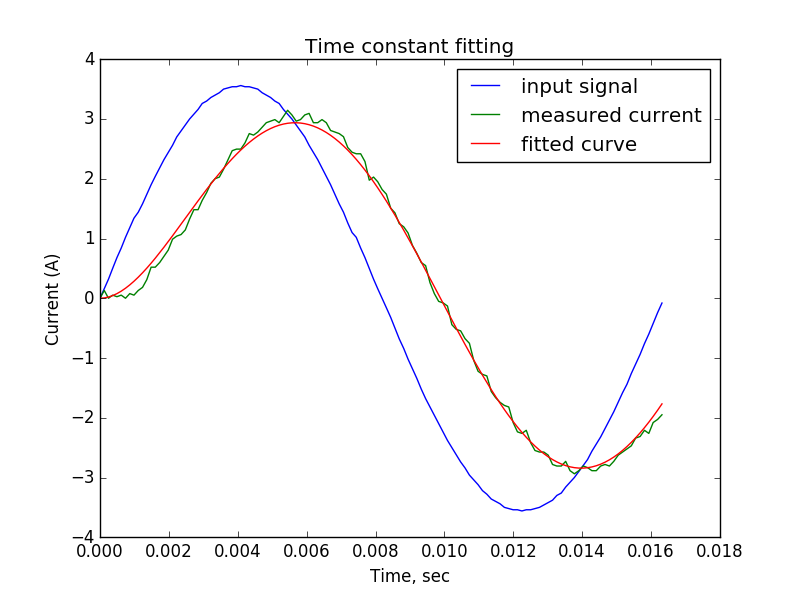
Conclusion

In general, the devil is not so terrible as he is painted. Many thanks to arastas for the science! In the foreseeable future I will try to find a little time to assemble the inverted pendulum not as it did (by controlling the voltage), but by directly controlling the current strength, this should simplify the calculations of the regulator of the pendulum itself.