New Bessel Derivatives Derived Using Wolfram Language

Almost two hundred years after Bessel introduced his functions of the same name, expressions were found for their derivatives with respect to parameters that are valid in the entire complex plane

In this blog, we give and comment on some previously unknown derivatives of special functions (primarily Bessel functions and related functions), as well as touch on the history and current state of differentiation with respect to parameters of hypergeometric and other functions. One of the main new formulas (in more detail below) is a closed expression for the first derivative of one of the most popular special functions - the Bessel function J :



Many functions of mathematical physics (that is, functions that are often used and therefore have special names) depend on several variables. One of them is usually called an argument, while the others are usually called parameters or sometimes indexes (icons). These special functions can have any number of parameters. For example (see Wolfram Functions Site ), the Bessel functions (z) and (z), Neumann (z), MacDonald (z), and Struve (z) and (z) have only one parameter (the so-called index), while while the Whittaker functions (z) and (z), as well as the degenerate hypergeometric functions (a; b; z) and U (a, b, z), have two parameters. Anger Functions (z) and(z), as well as Weber functions (z) and (z), can have one or two parameters (in the case of two parameters, they are called generalized Anger and Weber functions). The Appel and Humbert functions have three to five parameters, while the more complex special functions, such as the generalized hypergeometric function , can have any finite number of parameters.

Among other properties, differentiation of special functions plays an essential role, since derivatives characterize the behavior of functions when these variables change, and they are also important for studying the differential equations of these functions. As a rule, differentiation of a special function by its argument does not present significant difficulties. The largest collection of such derivatives, including the first, second, symbolic and even fractional order for more than 200 functions, is available in the section “Differentiation” on the Wolfram Functions website (let's say this section includes expressions for 21 derivatives of the Bessel function (z )), or in the book by Yu. A. Brychkov Handbook of Special Functions ). Most of these formulas are also available directly in the language.Wolfram Language . They can be obtained using the new MathematicalFunctionData and EntityValue functions .

However, derivatives with respect to parameters (as opposed to an argument) are generally much more difficult to calculate. It is noteworthy that the above formula, which includes the first-order derivative (with respect to the parameter ν ) of one of the most common special functions of mathematical physics, has only recently been found in closed form, and this, perhaps, an amazing fact indicates the complexity of the general problem. Thus, using the Bessel function J as a typical example, we will take a brief tour of the history of differentiation of this special function.

Computing derivatives is not always easy

Often people, even those familiar with mathematical analysis, tend to think that integration is difficult, and differentiation is easy. “Popular” wisdom is known, which states that “ differentiation is a matter of technology, and integration is art .” But this statement is completely true only for elementary functions, for which differentiation leads again to elementary functions (or their combinations). If differentiation is carried out by parameters, it usually leads to complex functions of a more general class.

The difference between differentiation and differentiation in the parameters of the argument can be illustrated by the Bessel functions J . Bessel derivative J with respect to its argument zhas been known for quite some time and has a relatively simple closed form:



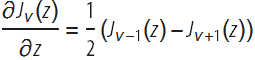
However, the analytical calculation of its derivative with respect to the parameter ν is more complicated. Often, derivatives with respect to parameters can be written in the form of an integral or an infinite series, but these objects cannot be represented in closed form through other simple or known functions. Historically, some special functions were introduced for the sole purpose of giving a simple notation for derivatives of known functions. For example, a polygamma function has emerged as a means of representing derivatives of a gamma function .

Generalized hypergeometric functionand its derivatives play an essential role in solving various problems of theoretical and applied mathematics (see, for example, the article by LU Ancarani and G. Gasaneo regarding the use of derivatives with respect to parameters in quantum mechanics). The generalized hypergeometric function generates, as special cases, many of the most commonly used elementary functions (for example, trigonometric, hyperbolic, logarithmic, and inverse trigonometric functions), as well as many special functions, including the Bessel, Struve, Kelvin, Anger-Weber, incomplete gamma function and integral functions (exponential, sine and cosine). In case p = 0 , q = 1 , the generalized hypergeometric functioncontains a family of Bessel functions (z), (z), (z), and (z). The Bessel function J , for example, has the following hypergeometric representation:







Interestingly, the history of function (z) begins almost exactly 200 years ago. In the reports of the Berlin Academy for 1816-17 (published in 1819), in the work of Analytische Auflösung der Keplerschen Aufgabe , Friedrich Wilhelm Bessel considers the so-called Kepler equation M = Ee sin (E), where M is the average anomaly, E is the eccentric anomaly, and e is the eccentricity of the Keplerian orbit. The solution to this equation can be represented (in modern notation) through Bessel functions of an integer order:



In this first work, Bessel still does not use modern notation, but his function appears already in an implicit form. For example, he uses the following sum (note that Bessel uses the Gauss notation for i ! ):



Nowadays, we can write this expression as the sum of two Bessel functions in Wolfram Language as follows:





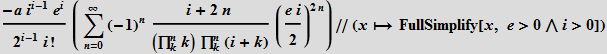
This sum is the first derivative of the function Bessel -2 ae (ei):





In his next work in 1824, Bessel uses almost modern notation (replacement J I ) to denote his function:







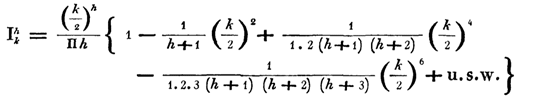
He also derives fundamental relations for this function, such as:







Various special cases of the general Bessel function are already found in the writings of Bernoulli, Euler, D'Alembert and others (see the article for more details ). The main reference book on Bessel functions to this day remains the classical monograph by G. N. Watson “ Theory of Bessel functions ”, which has been repeatedly reprinted and substantially supplemented in comparison with the first edition of 1922.

Thus, while the derivatives of the Bessel functions J with respect to the argument z were known from the beginning of the nineteenth century, only by the middle of the twentieth century were special cases found for derivatives by index. The derivatives of some Bessel functions with respect to ν at the points ν = 0,1,2, ... and ν = 1/2 were given by J. R. Airyin 1935, and the expressions for other functions of the Bessel family at these points are in the book of V. Magnus, F. Bateman and R. P. Soni “ Formulas and theorems for special functions of mathematical physics ” (1966):



Generalization to any half-integer values ν was presented at the International Conference on Abstract and Applied Analysis (Hanoi, 2002) as follows:



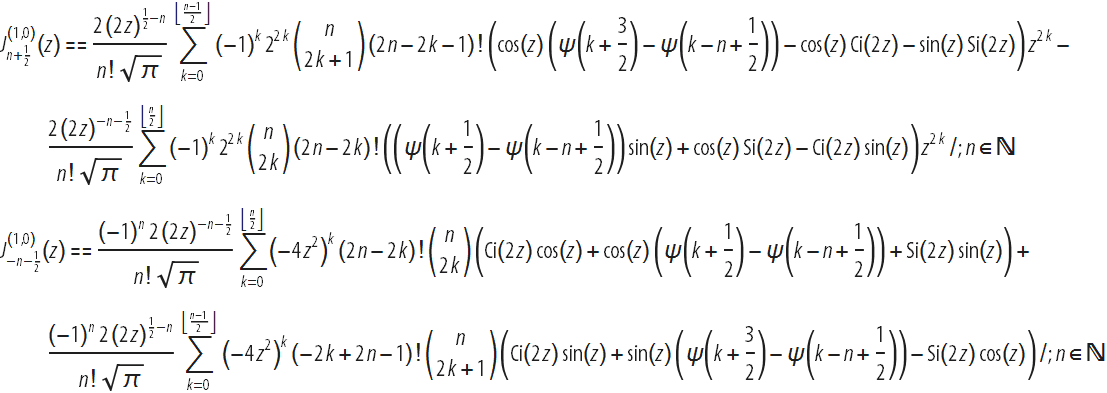
These results, along with expressions for derivatives with respect to the parameter of Struve functions at integer and half-integer points, were published in 2004-2005. Various new formulas for differentiating with respect to the parameters of the Anger and Weber functions, Kelvin functions, incomplete gamma functions, parabolic cylinder functions, Legendre and Gauss functions, generalized and degenerate hypergeometric functions can be found in the Handbook of Special Functions: Derivatives, Integrals, Series and others formulas . " For a brief overview and references, see H. Cohl .

It would probably seem surprising that, with all these results, the first derivatives of the Bessel functions in closed form for arbitrary values ​​of the parameter were obtained only in 2015 (Yu. A. Brychkov, ”Higher derivatives of Bessel functions with respect to the index “, 2016). They are expressed as combinations of products of Bessel functions and generalized hypergeometric functions. For example: The



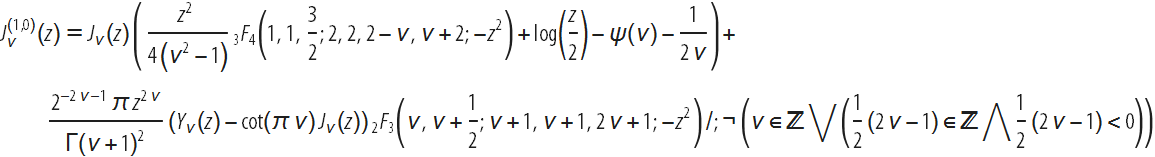
graphs below give some idea of ​​the behavior of the Bessel function (z) and its derivative in areas of interest. First, we give (in the real ν - z plane) the expression for the first derivative of (z) with respect to ν (see the equation at the beginning of the article):





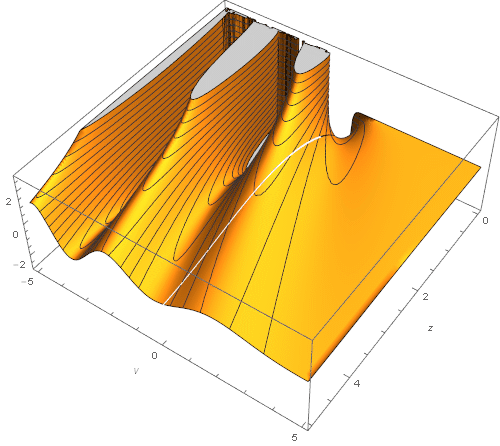
For a fixed index, namely ν = π , we give the graphs of the Bessel function together with its first two derivatives (by argument and index):





It is interesting to note that derivatives (byz and in ν ) have almost coincident zeros.

How did we get this?

It is noteworthy that even almost 300 years after the introduction of the classical function (the Bessel function (z) was introduced by Daniel Bernoulli in 1732), you can still find new and relatively simple formulas related to such functions. In fact, the formulas for the derivative introduced above (together with the corresponding results for the derivative , and the Neumann, MacDonald, and Kelvin functions) were obtained using the Wolfram Language. Detailed information on how these derivatives were searched is published here . In this post we give only a sketch of one of the options for the approach, which can be used for other special functions.

First, recall that the Bessel functions and others that we are now interested in are functions of the hypergeometric type; but differentiating the parameters of the general hypergeometric function of one variable requires more complex functions of the hypergeometric type of more than one variable (see the article by LU Ancarani and G. Gasaneo). The first derivative with respect to the “upper” parameters , and all derivatives of a symbolic integer order m with respect to the “lower” parameters of the generalized hypergeometric function, can be expressed in terms of the Campge de Ferrier hypergeometric function of two variables by the following formulas:





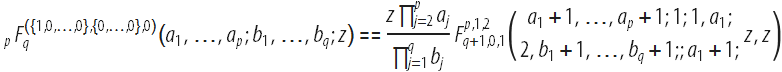
The above Campge de Ferrier hypergeometric function defined by a double row (seehere and here ):



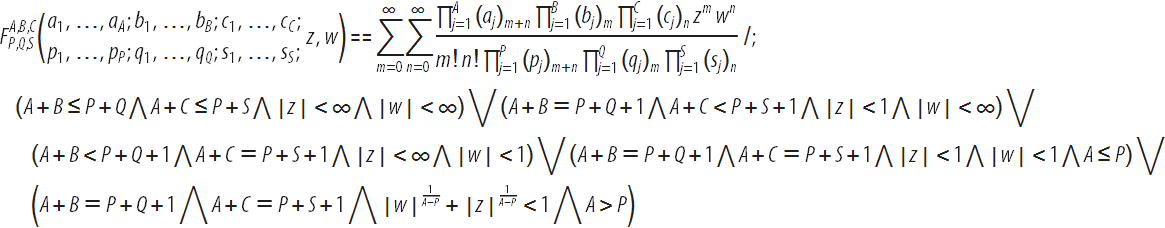
The Campa de Ferrier function can be considered as a generalization of a hypergeometric function to two variables: The



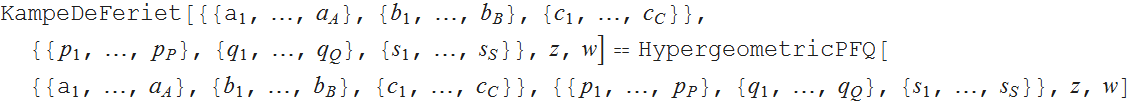
corresponding regularized version of the function can also be determined by replacing the product of the Pohhammer symbols in the denominator by .

The Campe de Ferrier function can be used to represent derivatives of the Bessel function J with respect to the parameter:



This expression coincides with the simple formula above, which includes hypergeometric functions of one variable, although this is not immediately obvious (we do not yet have a complete set of formulas to simplify multidimensional hypergeometric functions to expressions containing only one-dimensional hypergeometric functions).

Double series similar to the above definition of the generalized hypergeometric function of two variables also arise when calculating the Mellin transform of the products of three Meyer G-functions :



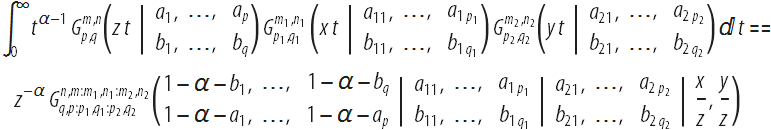
The right-hand side of this formula includes the Meyer G-function of two variables, which in the general (non-logarithmic) case can be presented as a finite sum of Campge de Ferrier hypergeometric functions with some coefficients, by analogy with two formulas ( first , second ) for the Meyer G-function of one variable. Finally, the Campe de Ferrier function also arises when the real and imaginary parts of hypergeometric functions are separated from one variable, z = x + iy , with real parameters:


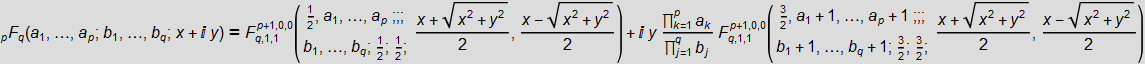
(the above formula was derived by E. D. Krupnikov, but not published).

It should be noted that in recent years, the hypergeometric functions of many variables are finding an increasing number of applications in areas such as quantum field theory, chemistry, mechanical engineering, communication theory and radar. Many practical results can be presented using such functions, and therefore most of the main results in this area are obtained in the applied scientific literature. The theory of such functions in theoretical mathematics is still relatively poorly developed.

Character derivatives in Wolfram Language

The author of these new and interesting symbolic derivative formulas, Yuri Brychkov, is a member of our team, which allows us to bring this constantly developing field of mathematics to the attention of our users. We are also lucky that we have at our disposal a new function of the Mathematica system (Wolfram Language) - Entity , which allows, among other things, to quickly (within a few weeks or days) present new results in a computable format and on all platforms where the language is used Wolfram Language, to our users. For example, in Mathematica, you can calculate the following expression:





Thus, we get the main formula of this article. We can verify the formula numerically by first substituting the symbolic values ​​ν and z, and having received the expression:





Next, we separate the left and right parts and substitute random values ​​for the argument and parameter: The





numerical derivative of the left side is calculated in Wolfram Language using the limiting procedure. The equality of the left and right sides, and therefore the correctness of the original formula for the derivative, are obvious.

In addition to the many new results regarding symbolic and parametric derivatives that were mentioned in this article and are only available through EntityValue(although a deeper integration of this functionality in future versions of the Wolfram Language requires constant effort), a large number of results in this area have already been implemented in the core of the Mathematica system and the core of the Wolfram Language. Such parameter derivatives are not automatically calculated because of their complexity, but they can be seen using the FunctionExpand command . For example:









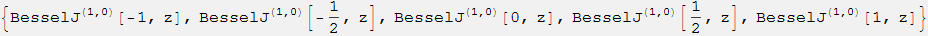
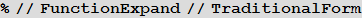
Derivatives of the second and higher order index of Bessel functions and related functions can be expressed in terms of the Campge de Ferrier hypergeometric function of two variables , but the formulas obtained can be quite complex and can include Bell Y polynomials :



The last expression arises from the representation of the Bessel function(z) through the composition function (; ν + 1; w) and :



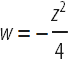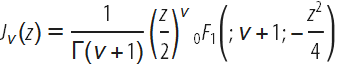
We use the formula Faa di Bruno , which allows to obtain an expression n th derivative compositions of m features . In the case m = 2 (see here and here ), we get, for example, the expression: The



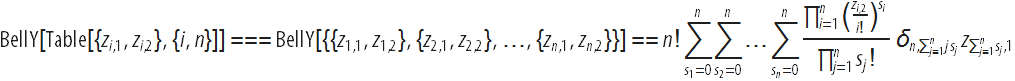
corresponding formula for the common m and n can be obtained and verified in the Wolfram Language:





While the Bell polynomials Y, for which there is no general closed form, are usually necessary for representing higher-order derivatives, one of the authors of this post, Yuri Brychkov, found a way to eliminate polynomials Y from n -th derivatives with respect to the parameter of Bessel functions, leaving us with a remarkable result:



for those interested in the convenience of users who would like to see in one place all the known formulas for the derivatives of special functions of the parameters (including those listed above), we have collected and Representat or the formula in the following ways:

1. In table format (download here ).

2. In the format of a Mathematica laptop (download here ).

3. A subset of the formulas that were known before 2009 can be seen on the Wolfram Function Site in the “Differentiation” sections of various functions (for example, see this page ).

In our next post we will give expressions of the closed form of derivatives for a collection of more than 400 functions with general rules for derivatives of symbolic and fractional order. We hope you enjoy exploring the world of derivatives of special functions with the Wolfram Language!

For questions about Wolfram technologies, write to info-russia@wolfram.com