Methods for determining whether a point belongs to a polygon
Recently on a habr there was an article in which it was described how it is possible to determine where a point is in relation to a polygon: inside or outside. A similar problem is encountered in geometric modeling and in computer graphics quite often. And since the method described in the article was somewhat not optimal, and there was little chaos in the comments, the idea arose to write this article. So, what algorithms exist in modern computer graphics to determine whether a given point belongs to a polygon or not.
Before starting, I want to describe the problem right away. Although the problem itself is simple: we have a set of points and an order in which these points are connected. And the point that we are testing for membership is given. It is understood that our polygon is closed, and in the general case the edges of the polygon do not intersect with each other, that is, it is spared it self-intersections. There are no restrictions on the number of vertices, that is, a polygon with a million vertices can easily be defined. We hope that the user will not ask us incomprehensibly what, but we cannot guarantee this either. And one more nuance: since we work with computer graphics, which means that we use floating-point arithmetic, which although it allows us to operate with numbers quite accurately, is still not free from errors.
Well, sort of decided on the problem, let's now see what methods of solution exist.
I'll start with the one that is considered the most popular in the world of graphics and games: ray tracing. In short, the algorithm can be described as follows:
Sounds easy, doesn't it? Indeed, this is the easiest method. As a result, it comes down to a certain number of intersections of a segment (a polygon face) and a ray, that is, in essence the intersection of two lines and testing of the resulting point for belonging to the ray and the segment. In the simplest case, you have to cross the beam with all the segments, when using trees (quadratic, binary or BVH), this number can be reduced. In general, it is said that the algorithmic complexity of this algorithm is O (log n), where n is the number of edges in the polygon.
The method is simple, but, unfortunately, in the general case it is better not to use it. The reason for this is the case when we intersect the vertex of a polygon with a ray or an edge that partially coincides with the ray. I illustrate this with an example.
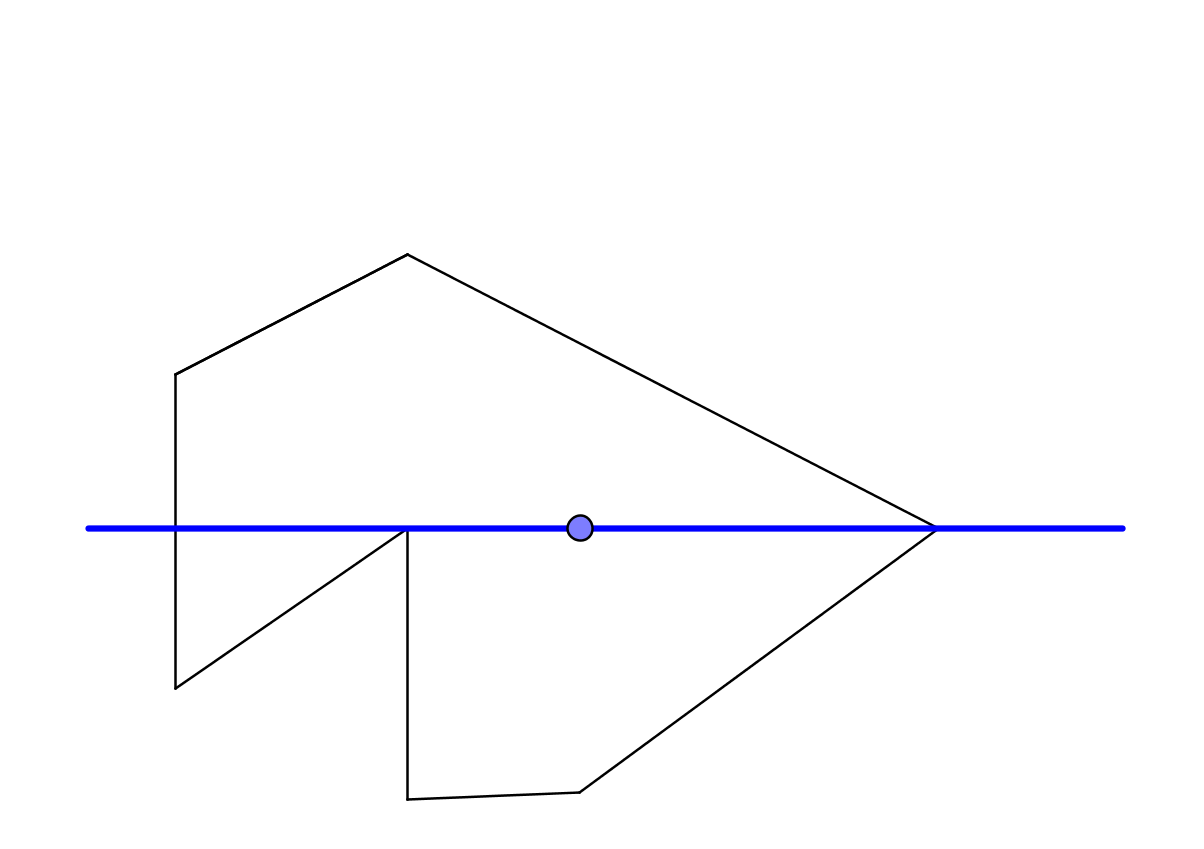
Suppose we have a polygon, and there is a point. At the very beginning, we agreed that the direction would be along the x axis. We release the ray from the point in the positive direction of the x axis and the ray safely intersects the polygon at the vertex. This begs the question, how exactly do we check this situation? Do not forget that we are working with floating point numbers, and small errors are possible. Let's move on to the world of analytic geometry so that you can operate not just with geometric concepts, but with numbers.
The equation of each segment (polygon face): a + t ( b - a ), where a are the coordinates of one end of the segment, b- coordinates of the other end of the segment. Obviously, if the ray intersects the segment, t must be in the interval [0,1]. If we cross a vertex with a ray, then t = 0 or t = 1. This is in the ideal world of mathematics. In the real world of computer algebra, you might end up with something like t = 1e-10. Or t = -1e-10. Or 0.99999999999998. Or 1.000000000000001. Since the intersection of two lines includes the division procedure, this can easily happen. And then what to do? Trust in the computer and assume that if we are strictly greater than or equal to zero or strictly less than or equal to unity, then we consider this an intersection, otherwise we do not consider it? We trusted and got a situation when the parameter t = -1e-20 with one edge and t = 1.000000000000000001 with the other edge. As a result of intersections, this is not considered
Let's look in the other direction. Sent a beam in a negative direction. It’s not very good there either - the ray crosses the vertex inside the polygon. It could also be anything. Instead of the horizontal direction, take the vertical? No one guarantees that you will not cross the peak again. In the example I specifically selected above, the point is selected in such a way that its intersection with a ray parallel to the y axis and going from top to bottom also intersects the polygon at the vertex.
And if you think that the intersection with the vertex is bad, see what else can happen:
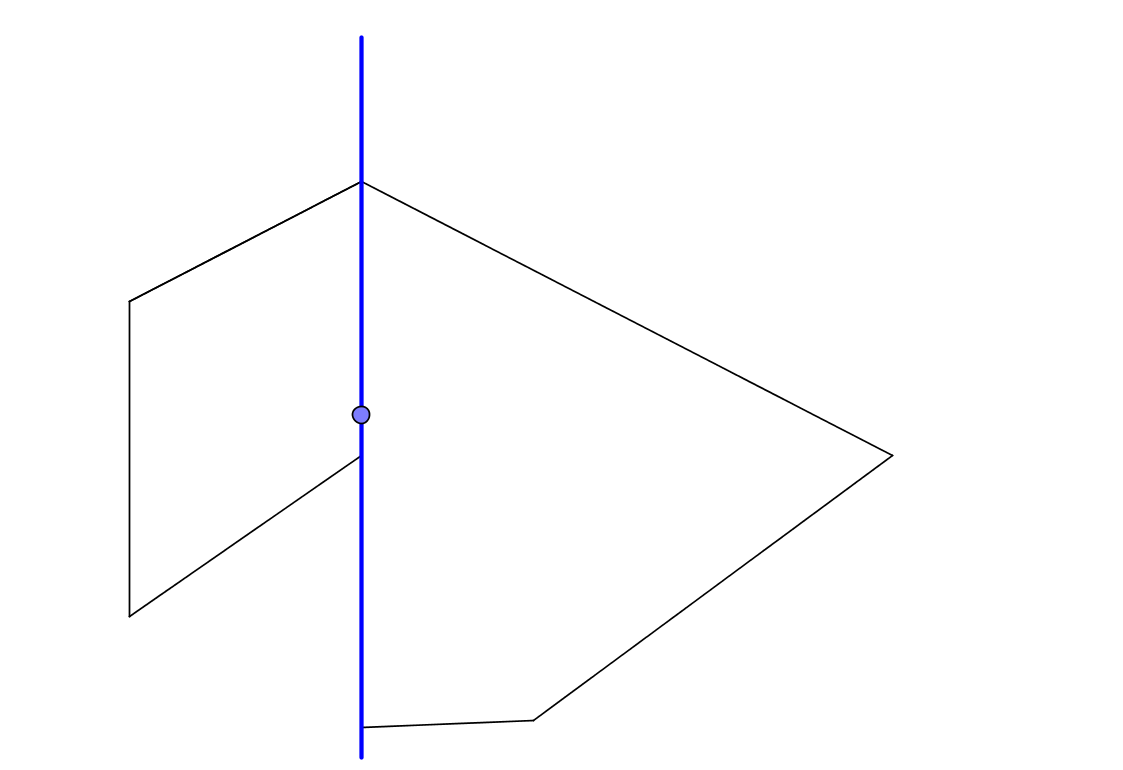
Here we intersect the ray with a segment that coincides with this ray. What to do in this case? And if it does not coincide, but almost coincides? And imagine that in a polygon there are many almost degenerate edges, how to intersect with such?
The saddest thing in this whole situation is that it seems to us: "I need something very simple for my simple goals, this situation will not affect me." According to Murphy’s law, unfortunately, such a situation arises whenever you do not expect it at all. And so I smoothly move on to the second method.
In general, this method has the terrible name angle weighted pseudo normals and it is connected in the concept of the so-called signed distance fields. But once again I do not want to scare anyone, so let it be just the near point and its normal (that is, a perpendicular vector).
The algorithm in this case is as follows:
Moreover, the angle as such is not necessary, it is enough to check the cosine of this angle. If positive - inside, if negative - outside. And since we are only interested in the cosine sign, we essentially compute the sign of the scalar product between two vectors.
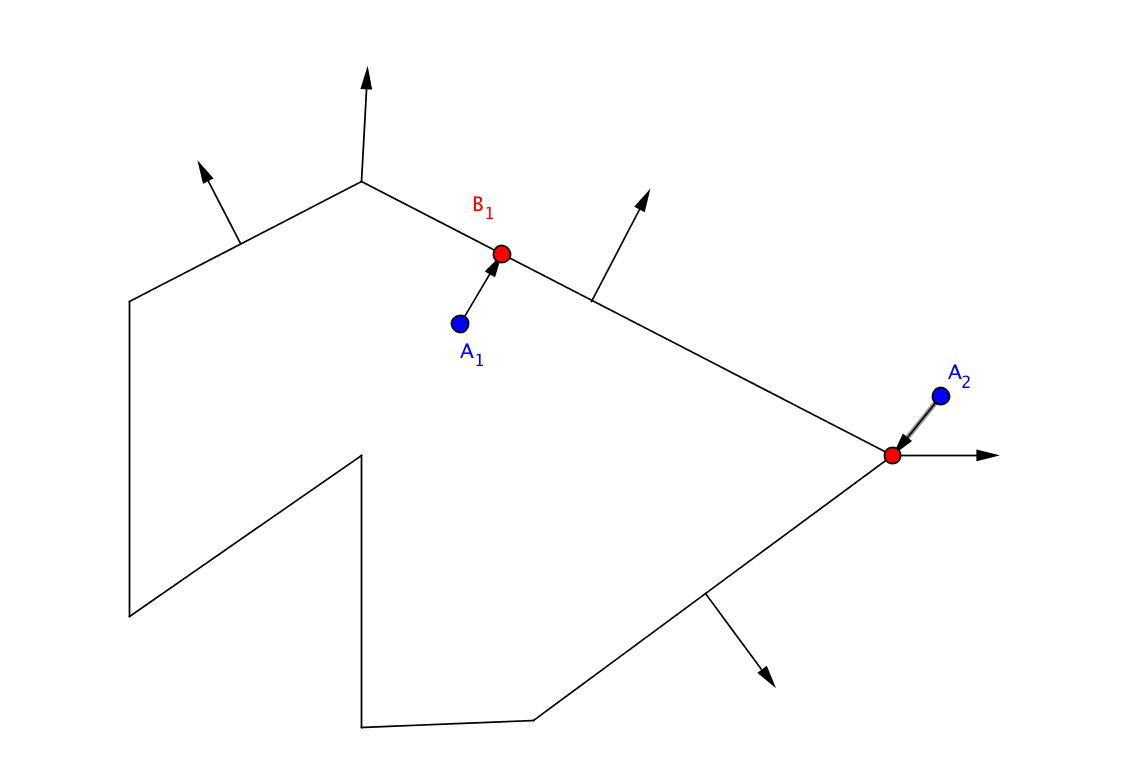
Consider an example. Point A1, the closest point to it is on an edge. If we do everything correctly, the normal to the edge is parallel to the vector from the tested point to the nearest one. In the case of point A1, the angle between the vectors = 0. Or almost zero, because everything is possible due to floating point operations. Less than 90 degrees, the test point A1 is inside. Test point A2. Its nearest point is a vertex, the normal to which is the average normal of the edges adjacent to this vertex. We consider the scalar product of two vectors should be negative. We are outside.
So, it seems to have sorted out the essence of the method. What about performance and floating point issues?
As with point tracing, performance is O (log n) if you use trees to store edge information. From a computational point of view, although it has a similar complexity, it will be somewhat slower than tracing. First of all, because the distance between a point and an edge is a little more expensive operation than crossing two lines. Floating-point troubles arise in this method, usually near the edges of a polygon. Moreover, the closer we are to the edge, the greater the likelihood of an incorrect determination of the sign. Fortunately, the closer we are to the edge, the smaller the distance. That is, if, for example, we say that if the distance obtained is less than a predetermined minimum (it can be a constant like DBL_EPSILON or FLT_EPSILON), then the point belongs to the edge. And if it belongs to a rib,
Describing the previous method, quite a lot has been said about the shortcomings. The time has come to name a few drawbacks of this method. First of all, this method requires that all normals to the edges be directed in the right direction. That is, before determining whether we are outside or inside, it is necessary to carry out some work on the calculation of these normals and their correct orientation. Very often, especially when there is a large dump of peaks and edges at the entrance, this process is not always simple. If you need to determine for only one point, the process of orientation of the normals can take most of the time that could be spent on something else. Also, this method really does not like when a polygon with self-intersections is fed to the input. In the beginning I said that in our problem such a case is not considered, but if it were considered,
But in general, the method is not bad, especially if we have a polygon with a large number of vertices and edges at the input, and there are many points to belong to. If there are few points, ray tracing is unstable, but you want something more or less reliable, that is, the third way.
This method has been known for a long time, but basically remains theoretical, for the most part because it is not as effective as the previous two. Here is its essence "on the fingers." Take the unit circle centered at the point under test. Then we project each vertex of the polygon onto this circle with the rays that pass through the vertex and the test point. Something like this:

In the figure, the points P1, P2 and so on are the vertices of the polygon, and the points P1 ', P2' and so on are their projections onto the circle. Now when we look at the edge of the polygon, we can determine from the projections whether the rotation is counterclockwise or clockwise when moving from one vertex to another. A counterclockwise rotation will be considered a positive rotation, and a clockwise rotation - negative. The angle that corresponds to each edge is the angle between the segments of the circle through the projections of the vertices of this edge. Since our turn can be positive or negative, the angle can also be positive or negative.
If after that all these angles are added, then the sum should be +360 or -360 degrees for a point inside and 0 for a point outside. Plus or minus here for a reason. If, when setting the traversal order, the polygon is bypassed counterclockwise, it should get +360. If the order of traversing the edges in the polygon is counterclockwise, then -360 is obtained. To avoid numerical errors, they usually do this: divide the resulting amount by 360 and lead to the nearest integer. The resulting number by the way is the very index of the point. The result can be one of three: -1 means that we are inside and go around the polygon clockwise, 0 means that we are outside, +1 means that we are outside. Everything else means that we were mistaken somewhere, or that the input data is incorrect.
The algorithm in this case is as follows:
Before starting, I want to describe the problem right away. Although the problem itself is simple: we have a set of points and an order in which these points are connected. And the point that we are testing for membership is given. It is understood that our polygon is closed, and in the general case the edges of the polygon do not intersect with each other, that is, it is spared it self-intersections. There are no restrictions on the number of vertices, that is, a polygon with a million vertices can easily be defined. We hope that the user will not ask us incomprehensibly what, but we cannot guarantee this either. And one more nuance: since we work with computer graphics, which means that we use floating-point arithmetic, which although it allows us to operate with numbers quite accurately, is still not free from errors.
Well, sort of decided on the problem, let's now see what methods of solution exist.
Method 1. Ray Tracing
I'll start with the one that is considered the most popular in the world of graphics and games: ray tracing. In short, the algorithm can be described as follows:
- From the tested point we issue a beam either in a predetermined or in an arbitrary direction.
- We count the number of intersections with the polygon.
- If the number of intersections is even, we are outside. If the number of intersections is odd, we are inside.
Sounds easy, doesn't it? Indeed, this is the easiest method. As a result, it comes down to a certain number of intersections of a segment (a polygon face) and a ray, that is, in essence the intersection of two lines and testing of the resulting point for belonging to the ray and the segment. In the simplest case, you have to cross the beam with all the segments, when using trees (quadratic, binary or BVH), this number can be reduced. In general, it is said that the algorithmic complexity of this algorithm is O (log n), where n is the number of edges in the polygon.
The method is simple, but, unfortunately, in the general case it is better not to use it. The reason for this is the case when we intersect the vertex of a polygon with a ray or an edge that partially coincides with the ray. I illustrate this with an example.

Suppose we have a polygon, and there is a point. At the very beginning, we agreed that the direction would be along the x axis. We release the ray from the point in the positive direction of the x axis and the ray safely intersects the polygon at the vertex. This begs the question, how exactly do we check this situation? Do not forget that we are working with floating point numbers, and small errors are possible. Let's move on to the world of analytic geometry so that you can operate not just with geometric concepts, but with numbers.
The equation of each segment (polygon face): a + t ( b - a ), where a are the coordinates of one end of the segment, b- coordinates of the other end of the segment. Obviously, if the ray intersects the segment, t must be in the interval [0,1]. If we cross a vertex with a ray, then t = 0 or t = 1. This is in the ideal world of mathematics. In the real world of computer algebra, you might end up with something like t = 1e-10. Or t = -1e-10. Or 0.99999999999998. Or 1.000000000000001. Since the intersection of two lines includes the division procedure, this can easily happen. And then what to do? Trust in the computer and assume that if we are strictly greater than or equal to zero or strictly less than or equal to unity, then we consider this an intersection, otherwise we do not consider it? We trusted and got a situation when the parameter t = -1e-20 with one edge and t = 1.000000000000000001 with the other edge. As a result of intersections, this is not considered
Let's look in the other direction. Sent a beam in a negative direction. It’s not very good there either - the ray crosses the vertex inside the polygon. It could also be anything. Instead of the horizontal direction, take the vertical? No one guarantees that you will not cross the peak again. In the example I specifically selected above, the point is selected in such a way that its intersection with a ray parallel to the y axis and going from top to bottom also intersects the polygon at the vertex.
And if you think that the intersection with the vertex is bad, see what else can happen:

Here we intersect the ray with a segment that coincides with this ray. What to do in this case? And if it does not coincide, but almost coincides? And imagine that in a polygon there are many almost degenerate edges, how to intersect with such?
The saddest thing in this whole situation is that it seems to us: "I need something very simple for my simple goals, this situation will not affect me." According to Murphy’s law, unfortunately, such a situation arises whenever you do not expect it at all. And so I smoothly move on to the second method.
Method 2. Near point and its normal
In general, this method has the terrible name angle weighted pseudo normals and it is connected in the concept of the so-called signed distance fields. But once again I do not want to scare anyone, so let it be just the near point and its normal (that is, a perpendicular vector).
The algorithm in this case is as follows:
- For the tested point, look for the nearest point on the polygon. At the same time, we remember that the nearest point can be not only on a segment, but also at a vertex.
- We are looking for the normal of the nearest point. If the near point lies on the edge, then the normal is a vector perpendicular to the edge and looking outward of the polygon. If the near point is one of the vertices, then the normal is the averaged vector of edges adjacent to the vertex.
- We calculate the angle between the normal of the nearest point and the vector from the tested point to the nearest. If the angle is less than 90 degrees, then we are inside, otherwise outside.
Moreover, the angle as such is not necessary, it is enough to check the cosine of this angle. If positive - inside, if negative - outside. And since we are only interested in the cosine sign, we essentially compute the sign of the scalar product between two vectors.

Consider an example. Point A1, the closest point to it is on an edge. If we do everything correctly, the normal to the edge is parallel to the vector from the tested point to the nearest one. In the case of point A1, the angle between the vectors = 0. Or almost zero, because everything is possible due to floating point operations. Less than 90 degrees, the test point A1 is inside. Test point A2. Its nearest point is a vertex, the normal to which is the average normal of the edges adjacent to this vertex. We consider the scalar product of two vectors should be negative. We are outside.
So, it seems to have sorted out the essence of the method. What about performance and floating point issues?
As with point tracing, performance is O (log n) if you use trees to store edge information. From a computational point of view, although it has a similar complexity, it will be somewhat slower than tracing. First of all, because the distance between a point and an edge is a little more expensive operation than crossing two lines. Floating-point troubles arise in this method, usually near the edges of a polygon. Moreover, the closer we are to the edge, the greater the likelihood of an incorrect determination of the sign. Fortunately, the closer we are to the edge, the smaller the distance. That is, if, for example, we say that if the distance obtained is less than a predetermined minimum (it can be a constant like DBL_EPSILON or FLT_EPSILON), then the point belongs to the edge. And if it belongs to a rib,
Describing the previous method, quite a lot has been said about the shortcomings. The time has come to name a few drawbacks of this method. First of all, this method requires that all normals to the edges be directed in the right direction. That is, before determining whether we are outside or inside, it is necessary to carry out some work on the calculation of these normals and their correct orientation. Very often, especially when there is a large dump of peaks and edges at the entrance, this process is not always simple. If you need to determine for only one point, the process of orientation of the normals can take most of the time that could be spent on something else. Also, this method really does not like when a polygon with self-intersections is fed to the input. In the beginning I said that in our problem such a case is not considered, but if it were considered,
But in general, the method is not bad, especially if we have a polygon with a large number of vertices and edges at the input, and there are many points to belong to. If there are few points, ray tracing is unstable, but you want something more or less reliable, that is, the third way.
Method 3. Index of a point relative to a polygon
This method has been known for a long time, but basically remains theoretical, for the most part because it is not as effective as the previous two. Here is its essence "on the fingers." Take the unit circle centered at the point under test. Then we project each vertex of the polygon onto this circle with the rays that pass through the vertex and the test point. Something like this:

In the figure, the points P1, P2 and so on are the vertices of the polygon, and the points P1 ', P2' and so on are their projections onto the circle. Now when we look at the edge of the polygon, we can determine from the projections whether the rotation is counterclockwise or clockwise when moving from one vertex to another. A counterclockwise rotation will be considered a positive rotation, and a clockwise rotation - negative. The angle that corresponds to each edge is the angle between the segments of the circle through the projections of the vertices of this edge. Since our turn can be positive or negative, the angle can also be positive or negative.
If after that all these angles are added, then the sum should be +360 or -360 degrees for a point inside and 0 for a point outside. Plus or minus here for a reason. If, when setting the traversal order, the polygon is bypassed counterclockwise, it should get +360. If the order of traversing the edges in the polygon is counterclockwise, then -360 is obtained. To avoid numerical errors, they usually do this: divide the resulting amount by 360 and lead to the nearest integer. The resulting number by the way is the very index of the point. The result can be one of three: -1 means that we are inside and go around the polygon clockwise, 0 means that we are outside, +1 means that we are outside. Everything else means that we were mistaken somewhere, or that the input data is incorrect.
The algorithm in this case is as follows:
- Set the sum of the angles to 0.
- For all edges of the polygon:
- Using the scalar product, we calculate the angle formed by the vectors starting at the test point and ending at the ends of the edges.
- We calculate the vector product of these same vectors. If its z-component is positive, we add the angle to the sum of the angles, otherwise we subtract from the same sum.
Divide the sum by 2 if we count in radians or by 360 if we count in degrees. The latter is unlikely, but suddenly.
Round the result to the nearest integer. +1 or -1 means we're inside. 0 means we are outside.
Consider an example. There is a polygon whose order is set counterclockwise. There is point A that we are testing. For testing, we first calculate the angle between the vectors AP1 and AP2. The vector product of these same vectors looks at us, so we add to the sum. We proceed further and consider the angle between AP2 and AP3. The vector product is looking at us, we subtract the resulting angle. Etc.
For this particular figure, I calculated everything and this is what happened:
Point A.
(AP1, AP2) = 74.13, (AP2, AP3) = 51.58, (AP3, AP4) = 89.99, (AP4, AP5) = 126.47, (AP5, AP1) = 120.99.
sum = 74.13-51.58 + 89.99 + 126.47 + 120.99 = 360. 360/360 = 1 Point - inside.
Point B.
(BP1, BP2) = 44.78, (BP2, BP3) = 89.11, (BP3, BP4) = 130.93, (BP4, BP5) = 52.97, (BP5, BP1) = 33.63.
sum = -44.78 + 89.11-130.93 + 52.97 + 33.63 = 0. The point is outside.
And traditionally we describe the pros and cons of this approach. Let's start with the cons. The method is simple mathematically, but not so effective in terms of performance. Firstly, its algorithmic complexity is O (n) and, whatever one may say, all the edges of the polygon will have to be sorted out. Secondly, to calculate the angle, you have to use the arccosine operation and the two operations of taking the root (the formula of the scalar product and its connection with the angle to help those who do not understand why). These operations are very expensive in terms of speed, and, moreover, the errors associated with them can be significant. And thirdly, the algorithm does not directly determine the point lying on the edge. Either outside, or inside. There is no third. However, the last drawback is easily determined: if at least one of the angles is equal to (or almost equal to) 180 degrees, this automatically means an edge.
The disadvantages of the method are somewhat offset by its advantages. Firstly, this is the most stable method. If the input polygon is correct, then the result is correct for all points, except perhaps the points on the edges, but see above about them. Moreover, the method allows you to partially deal with incorrect input data. Is the polygon self-intersecting? It doesn’t matter, the method will most likely determine most points correctly. A polygon is not closed, or not a polygon at all, but a meaningless set of segments? The method will determine the points correctly in a large number of cases. In general, the method is good for everyone, but slow and requires the calculation of arccosines.
How would you like to end this review? And the fact that there are not one or even two methods for solving the problem of determining whether a point belongs to a polygon. They serve different purposes and some are more suitable when speed is important, others when quality is important. Well, do not forget that we have unpredictable input data and we work with a computer whose floating-point arithmetic is subject to errors. If speed and quality are needed, it doesn’t matter at all - ray tracing is an aid. In most real-world applications, the near-point and normal method will most likely help. If in the first place is the accuracy of the determination with obscure input data, the point index method should help.
If you have any questions, ask. As a person who deals with geometry and similar problems related to graphics, I will be glad to help as I can.
