Overview of Local Binary Patterns (LBP) Image Descriptors and Variations
Good afternoon, Khabrovsk residents. I invite to cat programmers interested in computer vision and image processing. You may have missed a simple but effective mathematical tool for a low-level description of textures and setting their attributes for machine learning algorithms.
The topic of LBP has already been raised on Habré, however, I decided to spread the proposed explanation a bit and share some variations of this pattern.
As you know, a computer image is the same numerical information. Each pixel is represented by a number in the case of a black and white image or a triple of numbers in the case of a color. In general, they make a nice picture for the human eye and it’s convenient to carry out transformations over them, but often the information is too muchmany. For example, in object recognition problems, we are rarely interested in the value of each pixel individually: images are often noisy, and the desired images can be presented in different ways, so it is desirable that the algorithms are resistant to errors, the ability to capture the general trend. This property is called English-language sources robustness (robustness).
One way to deal with this problem is to pre-process the image, and leave only significant points, and apply the following algorithms to them. For this, SIFT, SURF, and other DAISY, feature descriptors were invented. With their help, you can stitch pictures, map objects and do a lot of useful things, but these descriptors have their drawbacks. In particular, it is expected that the found points will in a sense be truly special and unique, reproducing from image to image. You should not use SIFT to understand that both halves of this image are brick walls.

In addition, although these descriptors are called local, they still use a fairly significant area of the image. This is not good in terms of computational cost. Let's loosen this position a bit. Perhaps we can characterize the image, considering even smaller structures?
Again, we want to get a way to describe the structure of the picture, which
So what is a local binary pattern? In short: this is a way for each pixel to describe in which direction the brightness decreases. It’s not difficult to build it. Let’s do it.
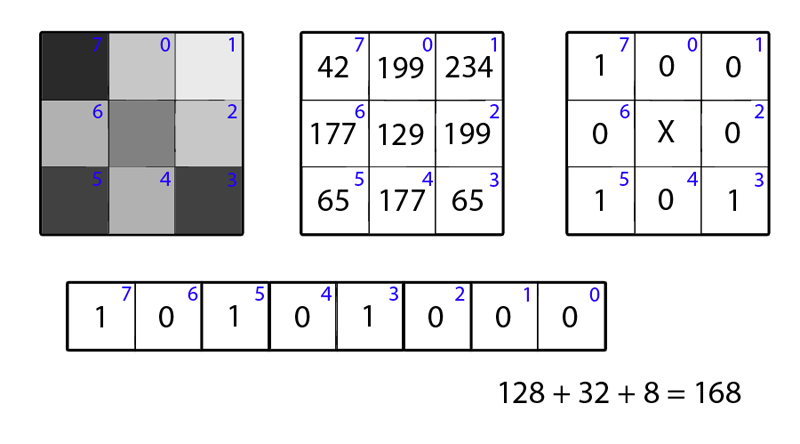
Wait a second, it's just a binary number! We will call it the clever words Local Binary Pattern (Timo Ojala, July 2002). From the point of view of mathematics, it looks like this:
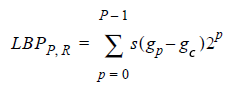
where s is the function step (x) (step), which returns 0 if and 1 if
and 1 if  .
.  Are the brightness values of the numbered neighbors of a pixel, and
Are the brightness values of the numbered neighbors of a pixel, and  - the brightness value of the most central pixel.
- the brightness value of the most central pixel.
That's all. A more mathematically savvy reader will call the descriptor bits the signs of the derivatives of brightness in directions, but this is unprincipled. It is clear that requirements 1-2 are trivially fulfilled. 3, probably, needs improvement, we will talk about this a little later. But what to do with 4? It’s not yet clear how to work with this. Yes, and we reduced the dimension of the task so-so: instead of a byte of pixel brightness values, we got a byte of signs of brightness changes in directions. There is no invariance in affine transformations, but we did not require it: in the end, the pattern of squares and rhombs is two different patterns.
From the obtained data, one can already extract something interesting, let's quickly see how to put them into practice, and based on this, we’ll think about how to improve them.
Use LBP where texture work is in progress. The most commonplace option: a texture is fed to the input of the program, and it determines what texture is in front of it. This may be one of the steps or an aid to a more complex algorithm. For example, the recognition algorithm on the image of an object that does not have a certain shape, but only a certain structure: fire, smoke or foliage (Hongda Tian, 2011). Alternative: use LBP when segmenting images in order to teach the machine to consider not every lane on a zebra as a unique object, but the whole zebra. See the forest behind the trees.
How exactly this happens depends on the task and the selected type of LBP. It does not always make sense to look for repeating patterns from LBP in the pictures, and certainly you should not compare the descriptors in one image with the descriptors in another. We plan to take immunity to noise by quantity, and this plays a trick on us: there are simply too many resulting codes. Good results can be obtained if you connect a neural network-auto-encoder (autoencoder) to the LBP card, it can extract more information from prepared patterns than from a raw picture. A simpler option is to rake all the resulting codes into one pile (build a histogram), and work with it already.
The latter approach at first looks strange. Is information lost when we just erase information about the relative position of microelements? In general, yes, it is possible to choose an example from three pictures that 1 and 2 are visually more similar, but 1 and 3 turn out to be more similar in the histogram, however, in practice this is unlikely.
A full histogram also often carries redundant information, so I advise you to arm yourself with the technique proposed in (S. Liao, May 2009) and developed in (Jinwang Feng, 2015):
In conclusion, I note that no one forces you to focus on textures. LBPs are successfully used instead of and together with Haar-like features in AdaBoost training. They capture high-frequency information that integrated tags miss.
So far, the choice of LBP as low-level information for machine learning looks unconvincing. It's time to fix the flaws we talked about above! For such a surprisingly simple descriptor like LBP, many variations have been invented during its existence.
We are faced with two conflicting tasks. First: reduce the number of patterns to make them easier to chew on the machine. Often we are interested in histograms, and if a histogram of 2 ^ 8 elements is acceptable, then out of 2 ^ 24 it takes a lot of space. Second: increase the information content of patterns. We would like to distinguish between distinct points of different types, and the more they differ, the stronger the patterns should differ. A separate item should be made noise immunity.
To begin with, we note that the most interesting thing for us is objects that the human eye can recognize: the boundaries of lines, angles, points, or spots. If you mentally place the center point on the edge of such an object and calculate the LBP, then at the stage of the circle you can see that zeros and ones are sort of divided into two groups. When the circle is “pulled”, a number is formed with 0, 1 or 2 transitions 0-1 or 1-0. For example, “00111100”, “11111111” and “01111111” refer to “good” patterns, while “10100000” and “01010101” do not.
Rejoice. Although it’s not that we are the only ones who have discovered this. The work that began the active study of LBP (Timo Ojala, July 2002) also noted that such patterns carry most of the relevant information. For them, they even came up with a special name: “uniform patterns” (uniform patterns). Their number is easy to calculate: for 8 neighbors we have 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 1 = 37 pieces ((P + 1) * P / 2 + 1). Plus one more mark under which we rake all the non-uniform patterns. It has become much nicer.
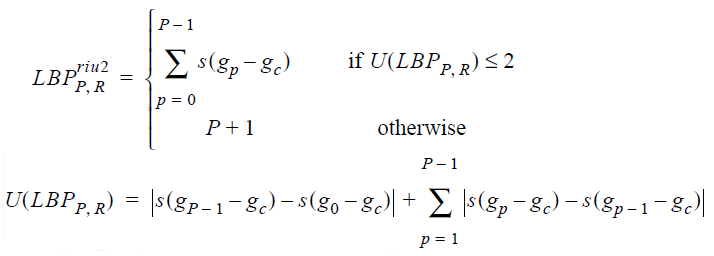
There are other ways to thin out a set of tags. For example, if for some reason we don’t want to remove non-uniform patterns, we can at least get rid of all the patterns obtained by rotating the image around the central pixel. It is enough to enter an unambiguous correspondence, which will display the LBP group in one. Say, we will consider the “real” pattern to be the one that has the minimum value during cyclic shifts to the right. Or to the left. As a gift, descriptor invariance with respect to rotation of the object is given. (Junding Sun, 2013)
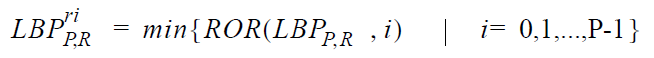
You can also accept the same patterns, for cases when the object and background change colors. Then we can consider the minimum of LBP and ~ LBP to be an “effective” pattern. This option was used in smoke detection work, which may look light gray against a dark background or dark gray against a white background (Hongda Tian, 2011).
In (Yiu-ming Cheung, 2014), it is generally proposed to get rid of extra neighbors and count ultra-local descriptors using only a couple of pixels, and then “collect” features by counting the co-occurrence matrix, but this is more like the usual calculation of the derivative with subsequent fraud over it. It seems to me that they are difficult to effectively put into practice.
Alternatively, you can consider the derivative of the brightness of the second order, it needs only 4 directions. Unfortunately, it is more prone to the negative effects of noise, and is less likely to carry significant information about the image. The application of this technique is also highly dependent on the task.
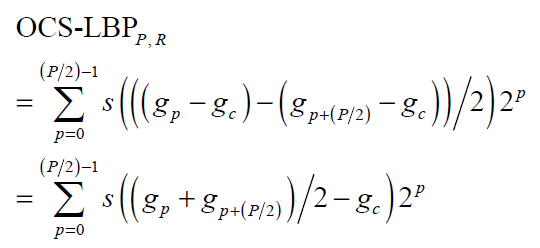
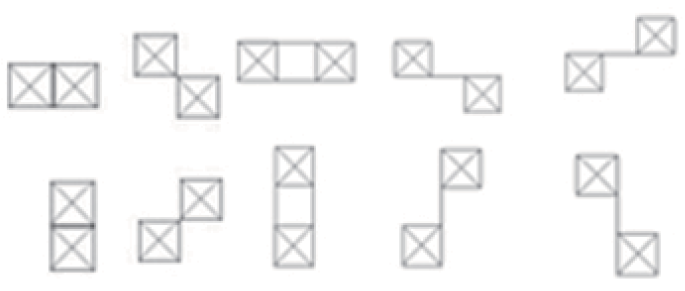
But in general, the idea of changing the way we consider the derivative was good. Let's try to return to the first derivative and introduce more stringent restrictions on the change of its sign. We will consider not the directions from the central pixel to the extreme, but the directions from the extreme pixels to the farthest from it (Junding Sun, 2013).
We will write a unit for a pixel if the brightness decreases from the first pixel to the central and from the central to the second. If the brightness increases or does not have a specific behavior - zero. Unfortunately, we lose information about bright and dark lonely points, but if we know that the image contains a lot of noise, this is even good.
In general, if a high noise level is expected, you can use more points to calculate the derivative, average with some weights with the values of neighbors or even pixel values outside the selected circle.
The way we check if the brightness changes also seems a little suspicious. In fact, if you simply use the sign of the derivative, then LBP will find phantom patterns even on an absolutely smooth image in the presence of even minimal noise. The usual way to deal with such a problem is to set a threshold value with which we compare the change in brightness between pixels. You can ask it from the outside, if there is additional information about the nature of the image, but this is not too cool, since typical fortune telling on the parameters begins. A more preferable option is to calculate the average value of the derivative over a certain neighborhood or the whole image and compare it with it (Jinwang Feng, 2015).
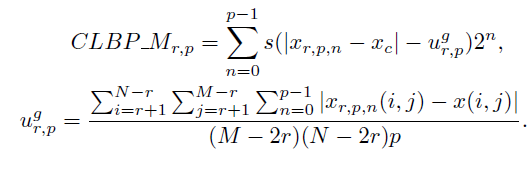
If desired, you can use more gradations, but this inflates the maximum number of patterns.
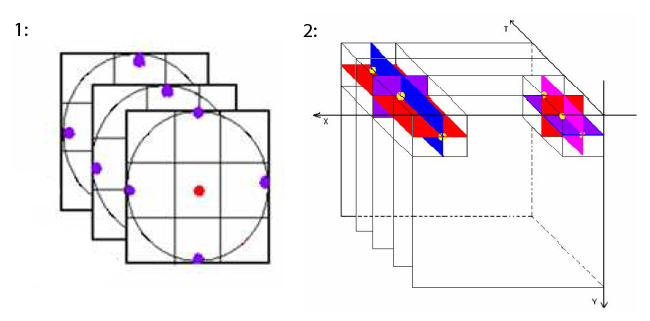
The Local Binary Pattern can be easily extended to the case of three dimensions (Xiaofeng Fu, 2012), (Guoying Zhao, 2007), (Xie Liping, July 2014). If you imagine the video as a “stack” of frames, then each pixel has not 8, but 9 + 9 + 8 = 26 neighbors (or less if you remove some corner pixels). There are different ways to obtain LBP in this case. The two most common are:
Finally, the result of some non-local filter can be attached to the descriptor. For example, in (Xie Liping, July 2014) Gabor filters are used for this. They are well suited for the detection of periodic structures, but they have certain disadvantages, in particular, they “call” on single lines. The correct combined use of LBP and global filters eliminates the disadvantages of both. On Habr you can read about the use of Gabor filters, for example, here and here .
Practice without theory is blind, but theory without practice is completely dead, so let's program something. This trivial Python 3.4 code (requires PIL, numpy and matplotlib) reads and displays the LBP histogram for the image. For simplicity of understanding, only optimization was used with setting the minimum difference in brightness proportional to the average difference in brightness in the image. From the result, DLBP can be calculated and used for machine learning, but overall, this is a very naive implementation. In real applications, the image needs preprocessing. Note that zeros, descriptors of a homogeneous region, are not written: there are almost always very, very many of them and they interfere with the normalization of the histogram. They can be used separately as a measure of texture scale.
The code:
Texture examples and results:
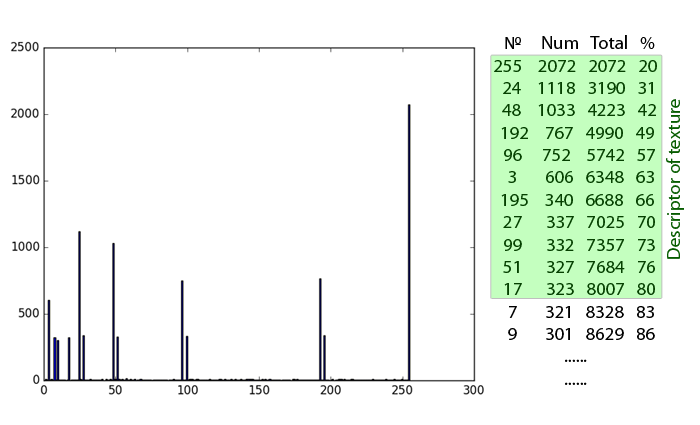
Note that the same bins often have the greatest values - they correspond to the uniform patterns discussed above. However, the distribution of them for different textures is different. The higher the noise level and the randomness of the texture, the more “garbage” LBPs (see small bins on histograms).
Introduction
The topic of LBP has already been raised on Habré, however, I decided to spread the proposed explanation a bit and share some variations of this pattern.
As you know, a computer image is the same numerical information. Each pixel is represented by a number in the case of a black and white image or a triple of numbers in the case of a color. In general, they make a nice picture for the human eye and it’s convenient to carry out transformations over them, but often the information is too muchmany. For example, in object recognition problems, we are rarely interested in the value of each pixel individually: images are often noisy, and the desired images can be presented in different ways, so it is desirable that the algorithms are resistant to errors, the ability to capture the general trend. This property is called English-language sources robustness (robustness).
One way to deal with this problem is to pre-process the image, and leave only significant points, and apply the following algorithms to them. For this, SIFT, SURF, and other DAISY, feature descriptors were invented. With their help, you can stitch pictures, map objects and do a lot of useful things, but these descriptors have their drawbacks. In particular, it is expected that the found points will in a sense be truly special and unique, reproducing from image to image. You should not use SIFT to understand that both halves of this image are brick walls.

In addition, although these descriptors are called local, they still use a fairly significant area of the image. This is not good in terms of computational cost. Let's loosen this position a bit. Perhaps we can characterize the image, considering even smaller structures?
main idea
Again, we want to get a way to describe the structure of the picture, which
- Quickly considered
- Invariant under luminance transformations that preserve order (
 )
) - Noise resistant
- Resistant to texture variations
- Strongly reduces the dimension of the task
So what is a local binary pattern? In short: this is a way for each pixel to describe in which direction the brightness decreases. It’s not difficult to build it. Let’s do it.

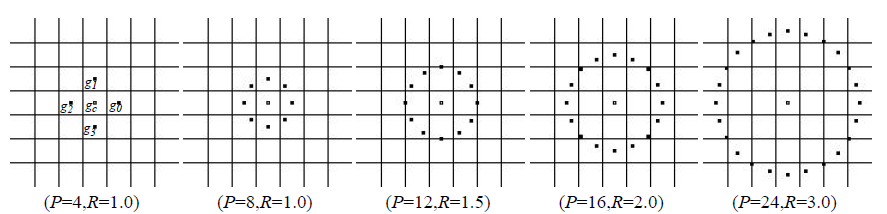
- First you need to choose the radius and the number of points ... stop-stop, who said "rogue"? Yes, just a couple of lines above I wrote that this descriptor is very local, but the definition of what is “very local” can vary from image to image. But so be it, let's stop at a radius of one: hereinafter for each pixel we will consider LBP based on 8 adjacent points.
- Number the selected points.
- Calculate the difference in brightness between each of the outermost pixels and the center.
- If the difference is negative (the brightness decreases), write one in the mind in the place of the neighbor; if non-negative (> = 0), it is zero.
- “Extend” the formed circle from zeros and ones into a line.

Wait a second, it's just a binary number! We will call it the clever words Local Binary Pattern (Timo Ojala, July 2002). From the point of view of mathematics, it looks like this:
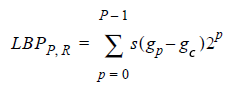
where s is the function step (x) (step), which returns 0 if
That's all. A more mathematically savvy reader will call the descriptor bits the signs of the derivatives of brightness in directions, but this is unprincipled. It is clear that requirements 1-2 are trivially fulfilled. 3, probably, needs improvement, we will talk about this a little later. But what to do with 4? It’s not yet clear how to work with this. Yes, and we reduced the dimension of the task so-so: instead of a byte of pixel brightness values, we got a byte of signs of brightness changes in directions. There is no invariance in affine transformations, but we did not require it: in the end, the pattern of squares and rhombs is two different patterns.
From the obtained data, one can already extract something interesting, let's quickly see how to put them into practice, and based on this, we’ll think about how to improve them.
Ok, I learned to count LBP. What's next?
Use LBP where texture work is in progress. The most commonplace option: a texture is fed to the input of the program, and it determines what texture is in front of it. This may be one of the steps or an aid to a more complex algorithm. For example, the recognition algorithm on the image of an object that does not have a certain shape, but only a certain structure: fire, smoke or foliage (Hongda Tian, 2011). Alternative: use LBP when segmenting images in order to teach the machine to consider not every lane on a zebra as a unique object, but the whole zebra. See the forest behind the trees.
How exactly this happens depends on the task and the selected type of LBP. It does not always make sense to look for repeating patterns from LBP in the pictures, and certainly you should not compare the descriptors in one image with the descriptors in another. We plan to take immunity to noise by quantity, and this plays a trick on us: there are simply too many resulting codes. Good results can be obtained if you connect a neural network-auto-encoder (autoencoder) to the LBP card, it can extract more information from prepared patterns than from a raw picture. A simpler option is to rake all the resulting codes into one pile (build a histogram), and work with it already.
The latter approach at first looks strange. Is information lost when we just erase information about the relative position of microelements? In general, yes, it is possible to choose an example from three pictures that 1 and 2 are visually more similar, but 1 and 3 turn out to be more similar in the histogram, however, in practice this is unlikely.
A full histogram also often carries redundant information, so I advise you to arm yourself with the technique proposed in (S. Liao, May 2009) and developed in (Jinwang Feng, 2015):
- Calculate descriptors for each pixel in the image
- Count their histogram
- Sort the bins of the histogram in descending order. Surprisingly, according to (S. Liao, May 2009), information about which particular bins can be discarded; the very distribution of them along the histogram carries enough information. You can not discard, in my opinion, so reliable.
- Leave the part of the histogram, which includes a certain predetermined percentage of patterns, discard the rest. The graphs in the same work argue that 80% is an acceptable number. The left part of the distribution ([bin number], its percentage amount) are the so-called dominant patterns (DLBP).
- DLBP can be fed to a neural network or SVM, which, using the magic of machine learning and a pre-provided training set, will determine what kind of texture is in front of it.

In conclusion, I note that no one forces you to focus on textures. LBPs are successfully used instead of and together with Haar-like features in AdaBoost training. They capture high-frequency information that integrated tags miss.
Variations
So far, the choice of LBP as low-level information for machine learning looks unconvincing. It's time to fix the flaws we talked about above! For such a surprisingly simple descriptor like LBP, many variations have been invented during its existence.
We are faced with two conflicting tasks. First: reduce the number of patterns to make them easier to chew on the machine. Often we are interested in histograms, and if a histogram of 2 ^ 8 elements is acceptable, then out of 2 ^ 24 it takes a lot of space. Second: increase the information content of patterns. We would like to distinguish between distinct points of different types, and the more they differ, the stronger the patterns should differ. A separate item should be made noise immunity.
Significant Patterns
To begin with, we note that the most interesting thing for us is objects that the human eye can recognize: the boundaries of lines, angles, points, or spots. If you mentally place the center point on the edge of such an object and calculate the LBP, then at the stage of the circle you can see that zeros and ones are sort of divided into two groups. When the circle is “pulled”, a number is formed with 0, 1 or 2 transitions 0-1 or 1-0. For example, “00111100”, “11111111” and “01111111” refer to “good” patterns, while “10100000” and “01010101” do not.
Rejoice. Although it’s not that we are the only ones who have discovered this. The work that began the active study of LBP (Timo Ojala, July 2002) also noted that such patterns carry most of the relevant information. For them, they even came up with a special name: “uniform patterns” (uniform patterns). Their number is easy to calculate: for 8 neighbors we have 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 1 = 37 pieces ((P + 1) * P / 2 + 1). Plus one more mark under which we rake all the non-uniform patterns. It has become much nicer.
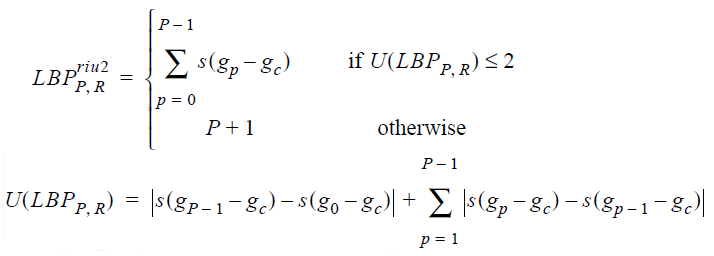
There are other ways to thin out a set of tags. For example, if for some reason we don’t want to remove non-uniform patterns, we can at least get rid of all the patterns obtained by rotating the image around the central pixel. It is enough to enter an unambiguous correspondence, which will display the LBP group in one. Say, we will consider the “real” pattern to be the one that has the minimum value during cyclic shifts to the right. Or to the left. As a gift, descriptor invariance with respect to rotation of the object is given. (Junding Sun, 2013)
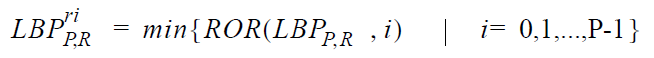
You can also accept the same patterns, for cases when the object and background change colors. Then we can consider the minimum of LBP and ~ LBP to be an “effective” pattern. This option was used in smoke detection work, which may look light gray against a dark background or dark gray against a white background (Hongda Tian, 2011).
In (Yiu-ming Cheung, 2014), it is generally proposed to get rid of extra neighbors and count ultra-local descriptors using only a couple of pixels, and then “collect” features by counting the co-occurrence matrix, but this is more like the usual calculation of the derivative with subsequent fraud over it. It seems to me that they are difficult to effectively put into practice.

Alternatively, you can consider the derivative of the brightness of the second order, it needs only 4 directions. Unfortunately, it is more prone to the negative effects of noise, and is less likely to carry significant information about the image. The application of this technique is also highly dependent on the task.
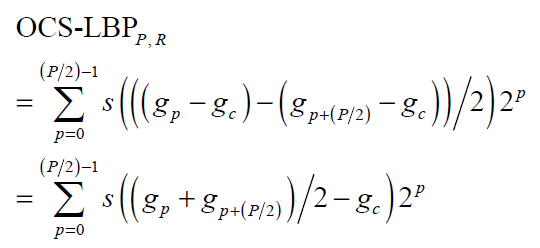
Noise resistance
But in general, the idea of changing the way we consider the derivative was good. Let's try to return to the first derivative and introduce more stringent restrictions on the change of its sign. We will consider not the directions from the central pixel to the extreme, but the directions from the extreme pixels to the farthest from it (Junding Sun, 2013).

We will write a unit for a pixel if the brightness decreases from the first pixel to the central and from the central to the second. If the brightness increases or does not have a specific behavior - zero. Unfortunately, we lose information about bright and dark lonely points, but if we know that the image contains a lot of noise, this is even good.
In general, if a high noise level is expected, you can use more points to calculate the derivative, average with some weights with the values of neighbors or even pixel values outside the selected circle.
The way we check if the brightness changes also seems a little suspicious. In fact, if you simply use the sign of the derivative, then LBP will find phantom patterns even on an absolutely smooth image in the presence of even minimal noise. The usual way to deal with such a problem is to set a threshold value with which we compare the change in brightness between pixels. You can ask it from the outside, if there is additional information about the nature of the image, but this is not too cool, since typical fortune telling on the parameters begins. A more preferable option is to calculate the average value of the derivative over a certain neighborhood or the whole image and compare it with it (Jinwang Feng, 2015).
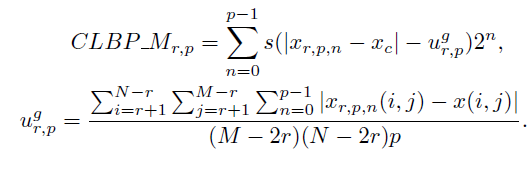
If desired, you can use more gradations, but this inflates the maximum number of patterns.
More information
The Local Binary Pattern can be easily extended to the case of three dimensions (Xiaofeng Fu, 2012), (Guoying Zhao, 2007), (Xie Liping, July 2014). If you imagine the video as a “stack” of frames, then each pixel has not 8, but 9 + 9 + 8 = 26 neighbors (or less if you remove some corner pixels). There are different ways to obtain LBP in this case. The two most common are:
- Three parallel planes. For each pixel i, j, we calculate the standard LBP in frames t-1, t, t + 1. Then we concatenate them and write them down, or if we are only interested in patterns that do not change from frame to frame, compare them with each other, and write only if the resulting LBPs are the same, otherwise we assign a “garbage” label.
- Three orthogonal planes. For each pixel (i, j, t), we consider three sets of neighbors: those lying in the frame, different in time, same in row, different in time, same in column. This method is more suitable for patterns that change over time. It requires more computational costs than the previous one.

Finally, the result of some non-local filter can be attached to the descriptor. For example, in (Xie Liping, July 2014) Gabor filters are used for this. They are well suited for the detection of periodic structures, but they have certain disadvantages, in particular, they “call” on single lines. The correct combined use of LBP and global filters eliminates the disadvantages of both. On Habr you can read about the use of Gabor filters, for example, here and here .
Example
Practice without theory is blind, but theory without practice is completely dead, so let's program something. This trivial Python 3.4 code (requires PIL, numpy and matplotlib) reads and displays the LBP histogram for the image. For simplicity of understanding, only optimization was used with setting the minimum difference in brightness proportional to the average difference in brightness in the image. From the result, DLBP can be calculated and used for machine learning, but overall, this is a very naive implementation. In real applications, the image needs preprocessing. Note that zeros, descriptors of a homogeneous region, are not written: there are almost always very, very many of them and they interfere with the normalization of the histogram. They can be used separately as a measure of texture scale.
The code:
(please forgive deviations from python style in the name of simplicity)
from PIL import Image
import matplotlib.pyplot as plt
import numpy as np
def compute_direction(x, y, threshold_delta):
return 1 if x - y > threshold_delta else 0
# 7 0 1
# 6 x 2
# 5 4 3
def compute_lbp(data, i, j, threshold_delta):
result = 0
result += compute_direction(data[i, j], data[i-1, j], threshold_delta)
result += 2 * compute_direction(data[i, j], data[i-1, j+1], threshold_delta)
result += 4 * compute_direction(data[i, j], data[i, j+1], threshold_delta)
result += 8 * compute_direction(data[i, j], data[i+1, j+1], threshold_delta)
result += 16 * compute_direction(data[i, j], data[i+1, j], threshold_delta)
result += 32 * compute_direction(data[i, j], data[i+1, j-1], threshold_delta)
result += 64 * compute_direction(data[i, j], data[i, j-1], threshold_delta)
result += 128 * compute_direction(data[i, j], data[i-1, j-1], threshold_delta)
return result
image = Image.open("test.png", "r")
image = image.convert('L') #makes it grayscale
data = np.asarray(image.getdata(), dtype=np.float64).reshape((image.size[1], image.size[0]))
lbps_histdata = []
mean_delta = 0
for i in range(1, image.size[1]-1):
for j in range(1, image.size[0]-1):
mean_delta += (abs(data[i, j] - data[i, j-1]) + abs(data[i, j] - data[i-1, j-1]) +
abs(data[i, j] - data[i-1, j]) + abs(data[i, j] - data[i-1, j+1]) )/4.0
mean_delta /= (image.size[1]-2) * (image.size[0]-2) #normalizing
mean_delta *= 1.5 #we are interested in distinct luminosity changes so let's rise up threshold
for i in range(0, image.size[1]):
for j in range(0, image.size[0]):
if i != 0 and j != 0 and i != image.size[1]-1 and j != image.size[0]-1:
tmp = compute_lbp(data, i, j, mean_delta)
if tmp != 0:
lbps_histdata.append(tmp)
hist, bins = np.histogram(lbps_histdata, bins=254, normed=True)
width = bins[1] - bins[0]
center = (bins[:-1] + bins[1:]) / 2
plt.bar(center, hist, align='center', width=width)
plt.show()
Texture examples and results:
More pixels
And what do you call textures ?! Well it's just patterns!
Well ...

Pictures are specially selected so that the similarities / differences are visible on the eye. It is also easy to see why there are many / few defined LBPs on a particular pattern.
Pattern 1

Pattern 1 + noise

Pattern 1 + even more noise and spots

Pattern 2

Pattern 3

Well ...

Pictures are specially selected so that the similarities / differences are visible on the eye. It is also easy to see why there are many / few defined LBPs on a particular pattern.
Pattern 1

Pattern 1 + noise

Pattern 1 + even more noise and spots

Pattern 2

Pattern 3

More pixels
Comparison of the LBP histograms of the first three pictures. The most characteristic bins are the same, but there are several spurious ones. Notice the large number of LBP = 255, black dots on a white background. Matches are marked in green, excess bins are marked in red.
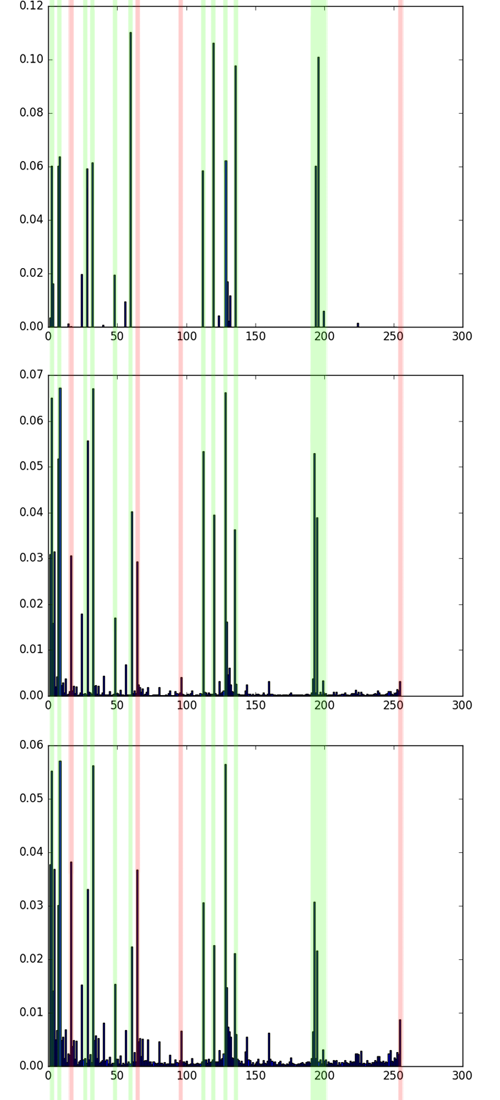
Comparison of histograms 4 and 5 of the picture, then comparison of histograms 1 and 4 of the picture. The matches are marked in green, the differences are marked in yellow. Although these pictures have different textures, 4 and 5 are unambiguously more similar than 1 and 4. This can be seen both by eye and by comparing the histograms.
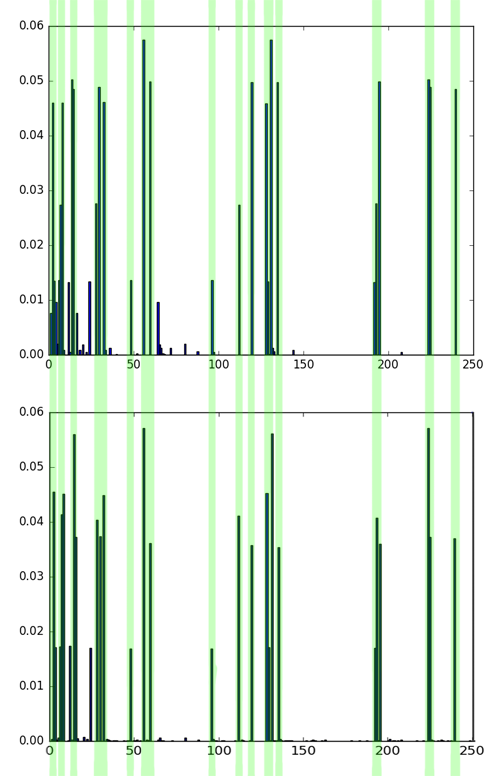
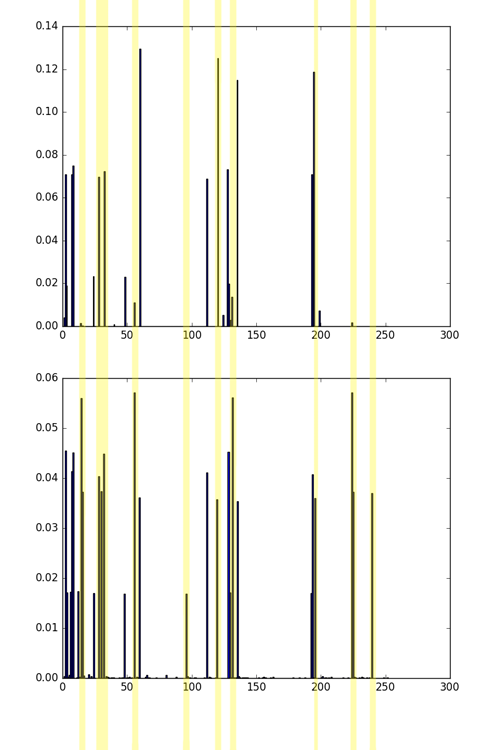

Comparison of histograms 4 and 5 of the picture, then comparison of histograms 1 and 4 of the picture. The matches are marked in green, the differences are marked in yellow. Although these pictures have different textures, 4 and 5 are unambiguously more similar than 1 and 4. This can be seen both by eye and by comparing the histograms.


Note that the same bins often have the greatest values - they correspond to the uniform patterns discussed above. However, the distribution of them for different textures is different. The higher the noise level and the randomness of the texture, the more “garbage” LBPs (see small bins on histograms).
List of sources
- Dong-Chen He, LN (1989). Texture Unit, Texture Spectrum, And Texture Analysis. Geoscience and Remote Sensing Symposium.
- Guoying Zhao, MP (2007). Dynamic Texture Recognition Using Local Binary Patterns with an Application to Facial Expressions. IEEE Transactions on Pattern Analysis and Machine Intelligence.
- Hongda Tian, WL (2011). Smoke Detection in Videos Using Non-Redundant Local Binary Pattern-Based Features. Wollongong, Australia: Advanced Multimedia Research Lab, ICT Research Institute.
- Jinwang Feng, YD (2015). Dominant – Completed Local Binary Pattern for Texture Classification. Materials of International Conference on Information and Automation. Lijiang, China.
- Junding Sun, GF (2013). New Local Edge Binary Patterns For Image Retrieval.
- S. Liao, MW (May 2009). Dominant Local Binary Patterns for Texture Classification. Transactions on Image Processing, Vol 18, No 5.
- T. Ojala, MP (1994). Performance evaluation of texture measures with classification based on Kullback discrimination of distributions. Vol. 1 - Proceedings of the 12th IAPR International Conference on Computer Vision & Image Processing.
- Timo Ojala, MP (July 2002). Multiresolution Gray Scale and Rotation Invariant Texture Classification. IEEE Transactions on Pattern Analysis and Machine Intelligence, 971-987.
- Xiaofeng Fu, RW (2012). Spatiotemporal Local Orientational Binary Patterns for Facial Expression Recognition from Video Sequences. International Conference on Fuzzy Systems and Knowledge Discovery.
- Xie Liping, WH (July 2014). Video-based Facial Expression Recognition Using Histogram Sequence of Local Gabor Binary Patterns from Three Orthogonal Planes. Proceedings of the 33rd Chinese Control Conference. Nanjing, China.
- Yiu-ming Cheung, JD (2014). Ultra Local Binary Pattern For Image Texture Analysis. Materials of IEEE International Conference on Security, Pattern Analysis, and Cybernetics. Wuhan, Hibei, China.
