Python CIS Symmetric Encryption Standards
The first weeks of the new year are the most suitable time to sit comfortably at the window to remember what the year that left us brought.
And he brought us two new encryption standards. Russian standard GOST R 34.12-2015 (block cipher Grasshopper). And the Ukrainian DSTU 7624: 2014 (block cipher Kalina). On cold, winter evenings you should not miss such a good reason to hang around. Under the cat is a brief description of the algorithms and their implementation in Python. And to make the new ciphers more fun, we dilute their society with the Belarusian STB 34.101.31-2007.
GOST R 34.12-2015
I propose to start with the Russian standard - the block cipher Grasshopper. The length of the input cipher block is 128 bits, the key length is 256 bits.
The following transformations are used in the cipher:
- X - bitwise addition modulo 2 with the key:
- The nonlinear transformation S is carried out by replacing each byte by substituting from the table π:
- The linear transformation L is realized using multiplication over the Galois field modulo a polynomial
:
Δ is a map that associates a binary field with an element of a finite field.
- a mapping that maps a binary string to an element of a finite field. 
When calculating the
operations of addition and multiplication are performed in the final field.
The procedure of encoding a 128-bit block of a formally described by the expression:
. Which, in a more visual form, looks like this:
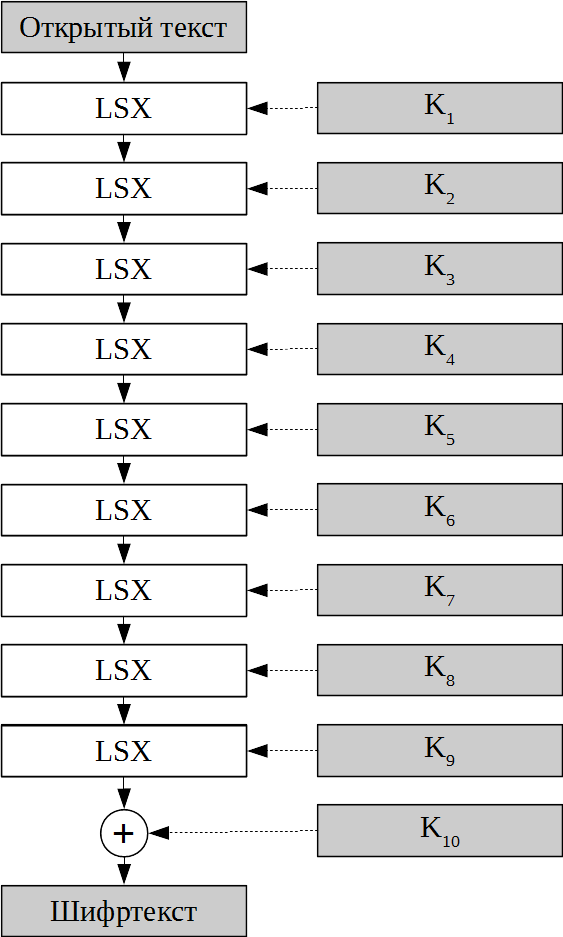
Round 128-bit keys K 1 , K 2 are obtained by splitting the main 256-bit key in half.
With their help, the following round keys are calculated:
When decrypting, inverse transformations are
used : An example of use in Python:
if __name__ == '__main__':
mtest = list(binascii.unhexlify('1122334455667700ffeeddccbbaa9988'))
ktest = list(binascii.unhexlify('8899aabbccddeeff0011223344556677fedcba98765432100123456789abcdef'))
gost =gost2015(ktest)
print('GOST 34.12-2015')
print(datetime.datetime.now())
c = gost.encryption(mtest)
d = gost.decryption(c)
print(datetime.datetime.now())
DSTU 7624: 2014
Introduced in July 2015 as the Ukrainian standard, the Kalina cipher supports several options for block length and key. Here I will describe a cipher version with a block length and a key length of 128 bits.
The internal state of the cipher is a matrix with 8 rows and 2 columns. Before encryption begins, the matrix is filled with plaintext bytes. Then, over the matrix elements, 10 rounds of the following transformations are performed.
- the addition of the columns of the state matrix with the columns of the round key, presented in the form of a matrix, modulo 2 64 .
(SubBytes) - replacing each byte of the state matrix by substituting from one of the four tables π 0 , π 1 , π 2 , π 3 .
(SiftRows) - a cyclic shift to the right by one position of the lines from the 4th to the 8th. 
(MixColumns) - conversion of state matrix columns. Each element of the new matrix is calculated by the formula:, 
where ⊗ is the scalar product of vectors, v is the vector,, 
G j is the matrix column. The operations of multiplication and addition are performed in a finite field modulo a polynomial
- bitwise addition modulo 2 of the matrix of the internal state of the cipher and the round key K v
The encryption process is described by the following expression:
Or in a more visual form:
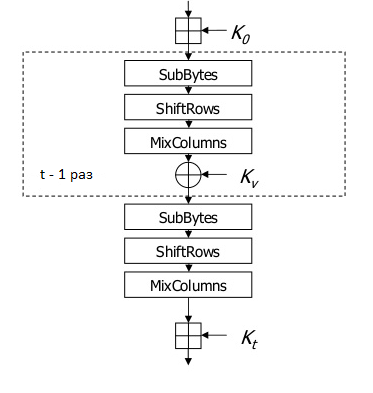
To generate round keys, first, using the master key K, the intermediate key is calculated
:, 
where 
for cases when the length of the block is equal to the length of the key. Keys for even rounds are generated based on the intermediate key:
where i is the number of the round, 
and 
0x01000100010001000100010001000100 The keys for odd rounds are calculated as follows:
where l is the length of the block. When decrypting, the inverse transformations are
used: Python example:
if __name__ == '__main__':
key = list(binascii.unhexlify('000102030405060708090a0b0c0d0e0f'))
pt = list(binascii.unhexlify('101112131415161718191a1b1c1d1e1f'))
dstu =dstu2014(key)
key2 = list(binascii.unhexlify('0f0e0d0c0b0a09080706050403020100'))
ct = list(binascii.unhexlify('1f1e1d1c1b1a19181716151413121110'))
dstu2 = dstu2014(key2)
print(datetime.datetime.now())
c = dstu.encryption(pt)
d = dstu2.decryption(ct)
print(datetime.datetime.now())
STB 34.101.31-2007
The BelT cipher, having a block length of 128 bits and a key length of 256 bits, was adopted as the standard for symmetric encryption of the Republic of Belarus in 2011. Encryption is performed by 8 rounds of transformations applied to the input block.
The encryption procedure consists of the following steps:
- The input block is written as
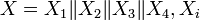
- The key is written in the form
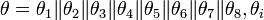and round keys are determined
- Additional variables a, b, c, d are assigned values
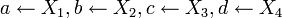
Where G r is the conversion operation of the 32-bit input string and
; RotHi r - cyclic left shift by r bits; H (u) - operation of replacing an 8-bit input string by substituting from a table; 
and 
- addition and subtraction operations modulo 2 32 .
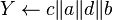returned as ciphertext.
When decrypting, the same operations are applied in reverse order.
Python usage example:
if __name__ == '__main__':
key = list(binascii.unhexlify('E9DEE72C8F0C0FA62DDB49F46F73964706075316ED247A3739CBA38303A98BF6'))
belt1 = belt(key)
m = list(binascii.unhexlify('B194BAC80A08F53B366D008E584A5DE4'))
key2 = list(binascii.unhexlify('92BD9B1CE5D141015445FBC95E4D0EF2682080AA227D642F2687F93490405511'))
belt2 = belt(key2)
c = list(binascii.unhexlify('E12BDC1AE28257EC703FCCF095EE8DF1'))
print(datetime.datetime.now())
c1 = belt1.encryption(m)
d1 = belt2.decryption(c)
print(datetime.datetime.now())
PS
An implementation of all the described algorithms in Python can be found on GitHub .