The book "Mathematical chaos. From elementary mathematics to sublime abstractions "

Can you imagine something bigger than the Universe, but at the same time quietly fitting in your head? What is it? Infinity! Eugenia Cheng takes us on an amazing mathematical journey to understand the most mysterious mathematical abstractions. Why are some numbers impossible to count? Why is infinity + 1 not the same as 1+ infinity? We will learn about the Grand Hotel's paradox, we will be able to feed 7 billion people with the help of a chessboard, and even get an infinite number of cookies from a small (final) piece of dough. All this will make it possible to understand and love such a strange and mysterious abstract mathematics. An incredible book about a huge and infinite Universe fascinates and intrigues, showing how one small mathematical symbol contains a huge idea.

Excerpt Infinitely small

One of the few subjects that I can see right now in front of me has nothing to do with mathematical analysis — this is my desk. The table existed long before the appearance of mathematical analysis, however, this particular table was made at the Ikea factory, which exactly uses mathematical analysis in its production. I want to say that the study of infinity may seem something abstract and outside of our world, literally and figuratively speaking (“figuratively,” as one of my friends likes to joke), but in the end it also leads us to the mathematical analysis is an integral part of our life.

The starting point for all this is thinking about objects that are "infinitely close to each other." When we draw a circle on a computer or type the letter O, they look smooth and even. But if we take a closer look at the images, they become pixel. This is the letter O on an enlarged scale on the screen of my computer.


We see a finite number of tiny squares disguised as a circle. My computer diligently forged a circle, he added a few dots of gray. A computer cannot do otherwise, because it is able to perceive and process only individual points in a finite amount and a fixed size.

What about our brains? The meaning of mathematical analysis is that our brain, in principle, is capable of more: we can perceive and process infinitely large numbers of objects, even if they are infinitely small. This is the topic we will now study.

Once I helped with mathematics in elementary Cambridge school on Park Street. I had to explain the symmetry to two six-year-olds. First, I asked them to draw symmetry lines on several triangles, then on a square, then on a pentagon, then on a hexagon. The funniest thing was when one of the babies said: “I know that an octahedron has eight sides, because the word octagon is like an octagon.” In the end I gave them a circle. One of the guys drew such a line on the circle:


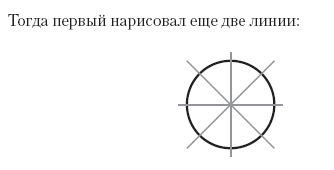
Then it became even more fun. The first child exclaimed: “There are hundreds of them!”, And the second said: “There are a million of them!”, After that the first one remarked: “You can draw your lines all your life and never finish!”, Then there was a pause, after which the second child raised a pencil, covered the whole circle with it and said: “Look! I finished! ”

I was confused, but I had to admit that they were both right. You can spend your whole life drawing symmetry lines on a circle and never finish, because there are an infinite number of them. In fact, there are an infinite number of them. We can see this. Imagine that we have determined where the line of symmetry passes by setting the angle that it forms with the horizontal.



We can take any angle - from 0 to 180 ° or in radians - any from 0 to π. If the angle is larger, the line will repeat one of those already drawn:



Take any real number from 0 to 180, and it does not have to be an integer or a rational number. We already know that there are uncountable real numbers from 0 to 180.

We will have an uncountable number of symmetry lines on a circle, but if you paint over the whole circle, you will actually paint them all. Perhaps now you thought it looked like a scam, because real lines of symmetry should intersect infinitely many times in the center of a circle, and we have infinitely many layers of pencil in the center. But if we do not pay attention to the center, but simply try to mark points along the edge of the circle, which are tangent to the line of symmetry, then it will be enough to draw a pencil around the edge of the circle. Do we draw in this way an infinitely large number of points? Will there be an infinitely large number of points in this line?

If so, how far apart are they? And if there is a finite amount, how many?

Division into infinity

If we divide the line into more and more segments, then the segments become less and less. Can we thus divide the line into an infinitely large number of segments? I want to say if we can do something infinitely small by dividing it into infinity.

Imagine a lottery in which all real numbers can fall. In the lottery drum there will be an infinite number of balls, but on each of them a definite final number will be indicated. In this case, the probability of winning will be rather strange. Usually in the lottery in the UK 6 of 59 balls fall out. There are approximately 45 million combinations, and all these combinations are equally likely. Your chance to win is 1: 45 million. This is a very small number (approximately 0.00000002), but not 0; although it seems to me that it is so close to 0 that it can actually be considered 0. If you multiply it again by the total number of possible combinations (45 million), you get 1, which is quite right, because this will be the probability of winning if you buy all lottery tickets.

There are an infinite number of combinations in the infinite lottery, so your chance to win will be equal to "1 to infinity". How to express it using a fraction? The answer can not be greater than 0, because if it were greater than 0, then multiplying it again by the total number of possible results (infinity), we get a number greater than 1. Does this mean that the probability of winning is 0? But someone can really win every time. You may fairly note that in practice such a lottery is impossible, but this argument of yours does not cancel this paradox. Everything here is exactly the same as with the hotel Gilbert: the fact that such a hotel cannot exist does not cancel the paradox.

We again returned to one of our first attempts to find infinity, asserting that


We know that such an equation generates a contradiction if we try to multiply both sides by 0. But now we want to say that the division by infinity gives 0 or


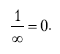
Now we already know more about infinity and immediately see that something is wrong with this equation. The problem here is that the way we tried to find infinity, namely, using an infinite set of objects, did not imply a division into infinity. The correct mathematical answer in this case should be: “Well, let's try it! If we have not done this yet, this does not mean that it is impossible. ”

Let's try to do the same as we did with the subtraction. Let us return to the idea that everything around is a multitude of objects. It's like counting on counting sticks: you can't break a counting stick in half (to the great disappointment of many children). If we take a lot of natural numbers, it is impossible to partially reduce it.

Remember, when we tried to express subtraction through infinity, we remembered the children's reasoning: 6 - 3 means "how much I have to count back, in order from 3 to return to 6 again." In other words, we solved the following equation: 3 + x = 6.

And now let's take 6: 3. We can consider 6: 3 in two different ways.

• How many times does 3 fit into 6? In other words, how many times should I add 3 to myself to make 6? It is like solving an equation like this: 3 × x = 6.
• Which number fits 6 exactly three times? In other words, what number can I add to myself three times to make 6? It is like solving an equation like this: x × 3 = 6.

In both cases the answer will be 2, because these formulations have no meaning if we are talking about finite numbers. But we already know that with infinity is not so simple. For example, adding 3 an infinite number of times is not the same thing as adding three times in infinity . That is, 3 × ω ≠ ω × 3.

Let's ask ourselves the question: “How many times should I add 3 to myself to get ω?” Answer: ω. Imagine that you are once again turned into a person who is handing out tear-off tickets in the queue. People come in groups of 3 people. How many groups of 3 people should come in order for you to run out of an endless bundle of tickets? Answer: ω. You will simply continue to give out 3 tickets to each group indefinitely.

If we look on the other hand: “What number can I add to myself 3 times to get ω?”, Then in this case there is no possible answer. If you add 3 finite numbers together, the answer will always be finite. If you add 3 infinite numbers together, each of them will be at least equal to ω (because ω is the smallest infinity), and together they will be even greater, it’s like “infinity and one more day”. We can look at it again with tear-off tickets. If one infinitely full bus arrives, you will spend your entire infinite pack of tear-off tickets on its passengers (at least). If after that another infinitely full bus arrives, you will be forced to take a pack with tickets of a different color.

Both of these questions were attempts to “divide infinity by 3,” but they gave us different answers. This proves that division, in the same way as multiplication, is not the best way to solve, if we are talking about infinity, even if it is just division by a small finite number. If instead we try to divide something into infinity, then everything will get worse. Suppose that we want to do the following: . Then we will have two options. First, how many times must we add ω to ourselves to get 1? This is obviously impossible, since ω is too much. The second option: what number can we add to ourselves ω the number of times to get 1? And again it will be absolutely impossible.

Notwithstanding the foregoing, it does seem that 1 divided by infinity should be equal to 0. Could this statement be a reasonable answer to the questions asked above? If we add ω to itself 0 times, we get nothing, so there is no point in this action. It will be like with 0 infinitely full buses, for them you will not need tear-off tickets at all. As for the second question: “Can we add 0 to ourselves ω times to make 1?”, Then everything will be as in the case with 0 people who queue an infinite number of times. You will not need any tear-off tickets for them again.

Then we could give up and say, “Okay, so- this is not a zero. Or try to act like a mathematician and say: “It all really seems reasonable, maybe we can give it some other mathematical meaning if our reasoning is not based on infinite sets?” One of the tasks of mathematics is to take what intuitively seems true, and give it an exact logical explanation. We should not give up so easily!

Reverse side of infinity

Perhaps now you are asking yourself the question why we cannot just think of something infinitely small and not equal to 0, because I used to say that we can create abstract things just by thinking about them. Mathematicians have already tried to apply this method, even though it seems meaningless (like the very idea of ​​infinity, which also seems meaningless until you begin to study it intensively enough). It looks like the other side of infinity. Infinity is greater than any number, and infinitesimally smaller than any number. If you add infinity to yourself, you will get infinity, and if you add an infinitely small value to yourself, you will again receive an infinitely small value. And if you multiply infinity by an infinitely small value, you get 1,

Such an approach gives rise to the same problems as our former “made-up” infinity. Here we need to act with extreme caution or rather with technical skill, as we did before, when we wanted to formulate a clear definition of the concept of "infinity", but since problems arise too often, it will be more elegant to try to get around them. If during a walk on your way there is a big muddy puddle, then you either step on it, hoping that the boots do not get wet, or try to bypass it. (Of course, some people, especially children, love to attack right on the center of the puddle. In mathematics, this also happens.)

Here's how to carefully circumvent the problem of dividing by infinity. Imagine that you need to divide the chocolate cake into several people. If you divide it into two, then everyone gets a lot. If you divide by three, then everyone still gets a lot, but less than in the first case. If they are four people, they will get even less. The more people, the less cake each one gets. If the number of people becomes really huge, it would be foolish to try to divide one unfortunate cake into all. Have you ever tried to divide a cake into a hundred people? (Wedding cakes usually consist of several tiers, which are essentially individual cakes.) What about the thousands of people? And a million? At some point, when there are too many people, everyone will get such a small piece,

If we have a million people and only one cake, then technically everyone will get their own piece - it will probably be billions of billions of cake molecules. But externally, the number of cake will be almost equal to 0, and with an increase in the number of people, it will increasingly tend to 0. So we gave a mathematical meaning to the idea that the division into infinity gives 0. In fact, we never divide into infinity (because that there is no common sense). Let's better go back to the example that we already talked about in chapter 11, when something tends to infinity. We tried to divide by what tends to infinity, and found that the answer will also tend to 0. Perhaps some clever people will now bring a microscope and say that they still see some cake on the plate. But we can always share it some more, and the cake will not be visible again. This does not mean that 1 divided by infinity is 0, but this reasoning gave our intuitive guesses a mathematical explanation, and from this the whole modern mathematical analysis began.

Paradoxes of Zeno

Mathematical analysis has its roots in ancient times. The question of how something can consist of an infinite number of infinitely small parts, even the Greek philosopher Zeno asked more than 2.5 thousand years ago. Just like Hilbert thousands of years later, Zeno studied paradoxes, proving that an infinite number of objects must be handled very carefully.

One of Zeno’s paradoxes is like a child’s thinking about chocolate cake: if I eat half of what’s left, then half of what’s left, and so on, then I’ll eat only half of what’s left, and does is it that the cake will become infinite?

Zeno formulates this paradox in the following way: if you want to get from point A to point B, you must first cover half the distance. Then you have to go half the remaining distance. After which you will have to go through half the new remaining distance, and so on. You constantly go only half the remaining distance.


After each stage, there is always half the distance left, and you can always walk only half of what’s left. Does this mean that you never get to the place?
Mathematicians love to create new concepts from old, already studied. Let's also go back to the already passed infinity of natural numbers. We said that we need to cover half of the entire distance, then a quarter, then one-eighth, one-sixteenth, and so on, "infinite." As we already know, natural numbers go on indefinitely. Suppose we need to go one mile. Then we can distinguish the following stages of the path:


We have an infinite number of n, which means we will have an infinite number of stages of the path. We cannot specify the length of each stage, but we can write it in a general form: for this we applied a formula with variable n. But if we cannot record the length of each stage, can we complete each of them? The answer must be: yes, because ending the path is quite normal for each of us. Usually we finish our ways, even the shortest, and we do it every day. (I do not leave the house every day, but sometimes I manage to go to the refrigerator several times in an hour.)

In a similar paradox, also formulated by Zeno, we are talking about Achilles and the tortoise, who run a race from point A to point B. The turtle is allowed to start moving first, say, at point A1, but it moves very slowly, because it is a turtle! But Achilles must first reach the place of the turtle start. During this time, the turtle goes a little further, for example, to point A2. Now Achilles must get to this point; while he does this, the turtle goes a little more, for example, to point A3. Now Achilles should get to A3, and during this time the turtle crawls to point A4. Every time Achilles reaches the place where the turtle was at the moment when we last checked the race status, the turtle goes a little further. Does this mean that the turtle wins the race?

Both of these paradoxes are built on quite logical evidence that leads to an absurd conclusion. Usually we are fully capable of reaching our destination. And it is obvious that if Usain Bolt runs a race with a turtle, he will win the race. The meaning of these paradoxes is not to detect errors in our reality, but to detect errors in the logic of our arguments.

This paradox is different from the paradox of the hotel Gilbert, which, although it can be filled, is still able to accommodate newly arrived guests. In it, the conclusion sounds absurd, because our intuitive ideas about endless hotels are not entirely correct.

Paradoxes like the paradox of the Gilbert Hotel are called true paradoxes; strong arguments in them lead to a conclusion that seems controversial, but in fact it is not. Paradoxes such as the Zeno paradox are called false paradoxes, in which a contradictory conclusion is derived from arguments that seem true, but are not such in reality.

In both cases, the essence of the paradox is to demonstrate the oddities that arise when we start thinking about infinity: in the paradox of the Hotel Gilbert we deal with infinitely large objects, and in Zeno's paradoxes with infinitesimally small ones. In the paradox of the Hilbert Hotel, we are faced with the problem of the infinite emergence of objects, which is impossible in real life, whether it be shoes, socks, tear-off tickets or hotel rooms. And in the paradoxes of Zeno, it begins to seem to us that objects arise infinitely, if we allow the reservation that in this case they become infinitely small. They cannot be infinitely small, because we do not know what it really means. But they can become infinitely small. Every day we are faced with endless sets of objects,

Infinitely large number of infinitely small objects

In the paradox of the path from point A to point B, we managed to reach the destination, which means that we were able to overcome an infinite number of segments of the path. However, this is possible only because these segments became smaller and smaller, and the time we spent on each segment also became smaller and smaller. And this happened in the real world, and not in the fantastic world of Gilbert, where we somehow have enough time to fill an infinite number of hotel rooms or issue an infinite number of tear-off tickets. In real life, we can do an infinite number of things every day, but only if the time we spend on each of them is infinitely small.

Imagine, for example, that you need to walk a mile to the train station. Let's say you go at a constant speed of 4 miles per hour. So it should take you 15 minutes. But what does Zeno's paradox say?

• First you have to go through the first half of a mile, which will take you 7.5 minutes.
• Then you will have to go the next quarter mile, which will take 3.75 minutes.
• Next you will have to go through one eighth of a mile, which will take you 1,875 minutes.
• After this, you will need to go through one sixteenth of a mile, which will take you 0.9375 minutes.
• ...

You have to go through all these infinitely decreasing sections of the path, but it takes you an infinitely decreasing amount of time. How long will you go through such small sections while you get to the train station? The answer is: infinitely many; if you stop after each final leg, there will always be some more.

Obviously, this is a completely absurd way to calculate how long it will take to get to the train station, especially because at some point the tiny distance that you still have to walk will be less than a foot. However, for us it is an important thought experiment, which demonstrates the following: it seems to us that an infinitely large number of objects can be put together and the final result can be obtained if these objects are constantly becoming less and less. In the real world, we will not be able to issue an infinite number of tear-off tickets, because all tear-off tickets are the same size. But even if they became less and less, we would still need a certain and separate period of time to issue each ticket, so we really can not do it. We cannot bite off one chocolate cake indefinitely, even if our “bites” become infinitely small, because the distance to our mouth will always be the same. (Although we can simultaneously reduce the distance to the mouth, but in the end everything will end with a chin on a plate with a cake.)

There are two riddles here. When does it make sense to add an infinitely large number of tiny objects? And how in such cases can we calculate the answer? This question, which had plagued mathematicians for thousands of years, was finally resolved in the 19th century with the advent of mathematical analysis. We will return to it in the next chapter.

»More information about the book can be found on the publisher's website
» Table of contents
» Fragment

For Habrozhiteley 25% discount on the coupon - Mathematics