Concurrent programming with CUDA. Part 3: Fundamental GPU algorithms: reduce, scan, and histogram

Content

Part 1: Introduction.
Part 2: GPU hardware and parallel communication patterns.
Part 3: Fundamental GPU algorithms: reduce, scan, and histogram.
Part 4: Fundamental GPU algorithms: compact, segmented scan, sorting. Practical application of some algorithms.
Part 5: Optimization of GPU programs.
Part 6: Examples of parallelization of sequential algorithms.
Part 7: Additional topics of parallel programming, dynamic parallelism.

The number of steps (steps) vs the number of operations (work)

Many Habr readers are probably familiar with the big O notation used to estimate the running time of algorithms. For example, they say that the runtime of a merge sorting algorithm can be estimated as O (n * log (n)) . In fact, this is not entirely correct: it would be more correct to say that the operating time of this algorithm when using one processor or the total number of operations can be estimated as O (n * log (n)) . For clarification, consider the algorithm execution tree:

So, we start with an unsorted array of nelements. Next, 2 recursive calls are made to sort the left and right half of the array, after which the sorted halves are merged, which is performed in O (n) operations. Recursive calls will be executed until the size of the sorted part is equal to 1 - an array of one element is always sorted. This means that the height of the tree is O (log (n)) and O (n) operations are performed at each level (at the 2nd level, 2 merges in O (n / 2) , at the 3rd level, 4 merges in O ( n / 4) , etc.). Total - O (n * log (n))operations. If we have only one processor (the processor refers to some abstract processor, not the CPU), then this is also an estimate of the execution time of the algorithm. However, suppose that we could somehow merge in parallel by several handlers - at best, we would divide O (n) operations at each level so that each handler performs a constant number of operations - then each level will execute for O ( 1) time, and the estimate of the execution time of the entire algorithm becomes equal to O (log (n)) !
In simple terms, the number of steps will be equal to the height of the algorithm execution tree (provided that operations of the same level can be performed independently of each other - therefore, in the standard form, the number of steps of the merge sort algorithm is not O (log (n)) - operations of the same level are not independent), but the number of operations - the number of operations :) Thus, when programming on the GPU it makes sense to use algorithms with fewer steps, sometimes even by increasing the total number of operations.
Next, we consider different implementations of 3 fundamental parallel programming algorithms and analyze them in terms of the number of steps and operations.

Convolution (reduce)

The convolution operation is performed on some array of elements and is determined by the convolution operator. The convolution operator must be binary and associative - that is, take 2 elements as input and satisfy the equality a * (b * c) = (a * b) * c , where * is the operator's designation (not to be confused with the commutativity property a * b = b * a ). The convolution operation on an array of elements a ₁ , ..., a _n is defined as (... ((a ₁ * a ₂ ) *a ₃ ) ... * a _n ) . The tree of execution of the sequential algorithm for the implementation of the convolution operation has the following form:

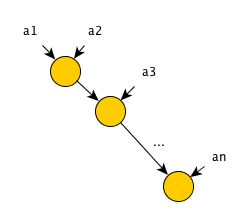
Obviously, for this algorithm, the number of operations is equal to the number of steps and is equal to n-1 = O (n) .
To “parallelize” the algorithm, it suffices to take into account the property of associativity of the convolution operator, and rearrange the brackets in places: (... ((a ₁ * a ₂ ) * a ₃ ) ... * a _n ) = (a ₁ * a ₂ ) * ( a ₃ * a ₄ ) * ... *(a _n-1 * a _n ) . That is, we can simultaneously calculate the values (a ₁ * a ₂ ) , (a ₃ * a ₄ ) and so on, and then perform a convolution operation on the resulting values. The execution tree of such an algorithm: The

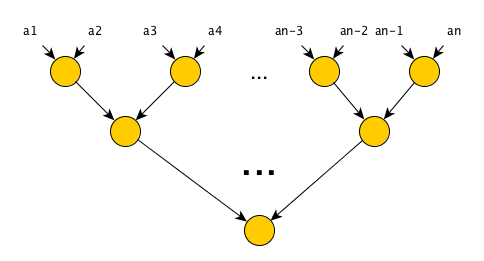
number of steps is now O (log (n)) , the number of operations is O (n) , which is good news - with a simple rearrangement of brackets, we got an algorithm with a significantly smaller number of steps, while the number of operations remains the same !

Scan

A scan operation is also performed on an array of elements, but is determined by the scan operator and an identity element . The scan operator must satisfy the same requirements as the convolution operator; the unit element must have the property I * a = a , where I is the unit element, * is the scan operator and a is any other element. For example, for the addition operator, the unit element will be 0, for the multiplication operator - 1. The result of applying the scan operation to the array of elements a ₁ , ..., a _n will be an array of the same dimension n. There are two types of scanning operations:

1. Including scanning - the result is calculated as: [reduce ([a ₁ ]), reduce ([a ₁ , a ₂ ]), ..., reduce ([a ₁ , ..., a _n ])] - in place i The ith input element in the output array will be the result of applying the convolution operation of all previous elements including the ith element itself .
2. Exclusive scan - the result is calculated as: [I, reduce ([a ₁ ]), ..., reduce ([a ₁ , ..., a _n-1 ])] - in place of the i- th input element in the output array the result of applying the convolution operation of all previous elements will be the exception of the i- th element itself - therefore, the first element of the output array will be a single element.

The scan operation is not so useful in itself, however, it is one of the stages of many parallel algorithms. If you have at your fingertips an implementation of just an inclusive scan and you need an exclusive one - just pass the array [I, a ₁ , ..., a _n-1 ] instead of the array [a ₁ , ..., a _n ] ; if vice versa, pass an array [a ₁ , ..., a _n , I]and discard the first element from the resulting array. Thus, both types of scanning are interchangeable. The tree of sequential implementation of the scan operation will look the same as the tree of execution of the convolution operation - just before each vertex of the tree, we will write the current result of the convolution ( a ₁ before the first calculation for the inclusive scan and I for the exclusive) to the corresponding position of the output array.
Therefore, the number of steps and operations of such an algorithm will be equal to n-1 = O (n) .
The easiest way to reduce the number of steps in the algorithm is quite straightforward - since the scan operation is essentially determined through the convolution operation, which just bothers usrun parallel version of convolution operation n times? In this case, the number of steps will actually decrease - since all convolutions can be calculated independently, the total number of steps is determined by the convolution with the largest number of steps - namely, the last one, which will be calculated on the entire input array. Total - O (log (n)) steps. However, the number of operations of such an algorithm is depressing - the first convolution will require 0 operations (not including memory operations), the second - 1, ..., the last - n-1 operations, total - 1 + 2 + ... + n-1 = (n-1) * (n) / 2 = O (n ² ) .
Consider 2 more efficient in terms of the number of operations algorithms for performing scan operations. The authors of the first algorithm are Daniel Hillis and Guy Steele, the algorithm is named after them - Hills & Steele scan. The algorithm is very simple, and can be written in 6 lines of python pseudocode:

def hillie_steele_scan(io_arr):
    N = len(io_arr)
    for step in range(int(log(N, 2))+1):
        dist = 2**step
        for i in range(N-1, dist-1, -1):
            io_arr[i] = io_arr[i] + io_arr[i-dist]

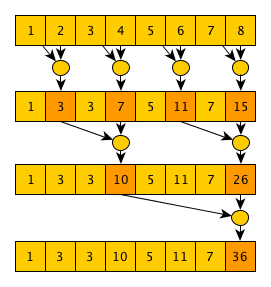
Or in words: starting from step 0 and ending with step log ₂ (N) (folding the fractional part), at each step step, each element under the index i updates its value as a [i] = a [i] + a [i-2 ^step ] (naturally, if 2 ^step <= i ). If you trace the execution of this algorithm for some array in your mind, it becomes clear why it is correct: after step 0, each element will contain the sum of itself and one neighboring element to the left; after step 1 - the sum of yourself and 3 neighboring elements on the left ... in step n - the sum of yourself and 2 ^{n + 1} -1 elements on the left - it is obvious that if the number of steps is equal to the integer part of log₂ (N), then after the last step we will get an array corresponding to the execution of the operation including scanning. It is obvious from the description of the algorithm that the number of steps is log ₂ (N) + 1 = O (log (n)) . The number of operations is (N-1) + (N-2) + (N-4) ... + (N-2 ^{log ₂ (N)} ) = O (N * log (N)) . The algorithm execution tree, using the example of an array of 8 elements and the sum operator, looks like this:

The author of the second algorithm is Guy Blelloch, the algorithm is called (whoever thought) - Blelloch scan. This algorithm implements the exclusivescanning is more complicated than the previous one, but it requires fewer operations. The main idea of ​​the algorithm is that if you carefully look at the implementation of the parallel convolution algorithm, you will notice that in the process of calculating the final value, we also calculate many useful intermediate values, for example, after the 1st step - the values a ₁ * a ₂ , a ₃ * a ₄ , ..., a _n-1 * a _n , after the 2nd step - the values a ₁ * a ₂ * a ₃ * a ₄ , a ₅ * a ₆ *a ₇ * a ₈ ... and so on. And if these values ​​are not thrown away, then we can very quickly calculate, for example, the convolution of the first six elements - just take the already calculated convolution values ​​of the first 4 elements and elements a ₅ , a ₆ and “collapse” them. Therefore, the algorithm consists of 2 phases - actually, the convolution phase, and the second phase, called down-sweep (something like "sweep down"). Graphically, the first phase looks as follows (using an example of the same array of 8 elements and the sum operator):

That is, a practically normal convolution algorithm, only intermediate convolutions calculated over the elements a _i , a _{i + 1} , ..., a_{i + k} replace the element a _{i + k} in the array.
The second phase is almost a mirror image of the first, but a “special” operator will be used that returns 2 values, and at the beginning of the phase the last value of the array is replaced by a single element (0 for the addition operator):

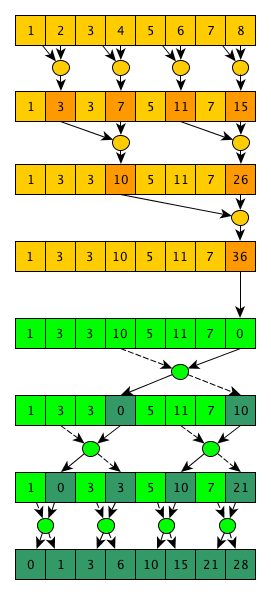
This "special" operator takes 2 values ​​- left and right, while as a left output value, it simply returns the right input, and as a right output, the result of applying the scan operator to the left and right input values. All these manipulations are needed in order to eventually correctly collapse the calculated intermediate convolutions and get the desired result - excluding scanning of the input array. As you can clearly see from this illustration of the algorithm, the total number of operations is N-1 + N-1 + N-1 = O (N) , and the number of steps is 2 * log ₂ (N) = O (log (N)). As usual, you have to pay for all the good (improved asymptotics in this case) - the algorithm is not only more complicated in the pseudo-code, but it is also more difficult to efficiently implement on the GPU - in the first steps of the algorithm we have a lot of work that can be done in parallel; when approaching the end of the first phase and at the beginning of the second phase, very little work will be performed at each step; and at the end of the second phase we will again have a lot of work at each step (by the way, several more interesting parallel algorithms have such a execution pattern). One of the possible solutions to this problem is to write 2 different cores - one will only perform one step, and be used at the beginning and at the end of the algorithm; the second will be designed to perform several steps in a row and will be used in the middle of execution - at the transition between phases.

Histogram

Informally, a histogram in the context of GPU programming (and not only) refers to the distribution of an array of elements over an array of cells, where each cell can contain only elements with certain properties. For example, having data on basketball players, such as height, weight, etc. we want to know how many basketball players have a height of <180 cm, from 180 cm to 190 cm and> 190 cm.
As usual, the sequential algorithm for calculating the histogram is quite simple - just go through all the elements in the array, and increase for each element by 1 value in the corresponding cell. The number of steps and operations is O (N) .
The simplest parallel algorithm for calculating a histogram is to start upstream on an array element, and each stream will increase the value in the cell only for its element. Naturally, in this case it is necessary to use atomic operations. The disadvantage of this method is speed. Atomic operations force threads to synchronize access to cells, and as the number of elements increases, the efficiency of this algorithm will decrease.
One of the ways to avoid the use of atomic operations in constructing a histogram is to use a separate set of cells for each stream and subsequent convolution of these local histograms. The disadvantage is that with a large number of threads, we may simply not have enough memory to store all the local histograms.
Another option to increase the efficiency of the simplest algorithm takes into account the specifics of CUDA, namely that we run threads in blocks that have shared memory, and we can make a common histogram for all threads in one block, and add at the end of the kernel using all the same atomic operations this bar graph to global. And although it is still necessary to use atomic operations on the general memory of the block to construct a general histogram of a block, they are much faster than atomic operations on global memory.

Conclusion

This part describes the basic primitives of many parallel algorithms. The practical implementation of most of these primitives will be shown in the next part, where as an example we write bitwise sorting.