July 16, 2014 at 19:52Probabilistic Models: LDA, Part 2
We continue the conversation. The last time we made the first step in the transition from a naive Bayesian classifier to LDA: removed from the naive Bayes need for a training set of markup, making it a clustering model that can teach the EM algorithm. Today I have no more excuses - I have to talk about the LDA model itself and show how it works. Once we talked about the LDA on this blog, but then the story was very short and without very significant details. I hope that this time I will be able to tell more and more clearly.
So, we are starting a conversation about LDA. Let me remind you that the main goal of our generalization is to ensure that the document is not rigidly attached to one topic, and the words in the documents could come from several topics at once. What does this mean in (mathematical) reality? This means that the document is a mixture of topics, and each word can be generated from one of the topics in this mixture. Simply put, we first throw the document cube, determining the topic for each word , and then pull the word out of the corresponding bag.
Thus, the main intuition of the model looks something like this:
Since intuition is the most important thing, and here it is not the simplest, I will repeat again the same thing in other words, now a little more formally. Probabilistic models to understand and convenient to represent a generative process (generative processes), when we consistently describe how the data is generated by one unit, introducing therein all probability assumptions that we make in this model. Accordingly, the generating process for the LDA should consistently describe how we generate each word of each document. And this is how it happens (hereinafter I will assume that the length of each document is specified - it can also be added to the model, but usually it does not give anything new):
Here, the process of choosing a word for given θ and φ should already be clear to the reader - we throw a cube for each word and select the topic of the word, then we pull out the word itself from the corresponding bag:
In the model, it remains only to explain where these θ and φ come from and what means expression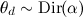
; at the same time it will explain why this is called Dirichlet allocation.
Johann Peter Gustav Lejeune Dirichlet was not so much involved in probability theory; he mainly specialized in mathematics, number theory, Fourier series, and other similar mathematics. In probability theory, he was not so often seen, although, of course, his results in probability theory would have made a brilliant career for modern mathematics (trees were greener, sciences were less studied, and, in particular, mathematical Klondike was not exhausted either). However, in his studies of mathematical analysis, Dirichlet, in particular, managed to take such a classical integral, which as a result was called the Dirichlet integral:
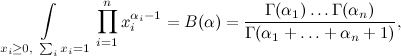
where Γ (α i ) is the gamma function, the continuation of the factorial (for natural numbers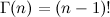
) Dirichlet himself derived this integral for the needs of celestial mechanics, then Liouville found a simpler conclusion, which was generalized to more complex forms of integrands, and wrap it all up.
The Dirichlet distribution motivated by the Dirichlet integral is the distribution on the ( n -1) -dimensional vector x 1 , x 2 , ..., x n -1 , defined in this way:
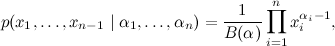
where
, and the distribution is given only on ( n -1) -dimensional simplex, where x i > 0. From it the Dirichlet integral a normalization constant appeared in it. And the meaning of the Dirichlet distribution is rather elegant - this is the distribution on the distributions. Look - as a result of sketching a vector over the Dirichlet distribution, we get a vector with non-negative elements, the sum of which is unity ... bah, but this is a discrete probability distribution, actually a dishonest cube with n faces.
Of course, this is not the only possible class of distributions on discrete probabilities, but the Dirichlet distribution also has a number of other attractive properties. The main thing is that it is a conjugate a priori distribution for that very dishonest cube; I will not explain in detail what this means (possibly later), but, in general, it is reasonable to take the Dirichlet distribution as an a priori distribution in probabilistic models, when I want to get an unfair cube as a variable.
It remains to discuss what, in fact, will be obtained for different values of α i . First of all, let's just confine ourselves to the case when all α i are the same - we have a priori no reason to prefer some topics to others, at the beginning of the process we still don’t know where which topics will stand out. Therefore, our distribution will be symmetrical.
What does it mean - distribution on a simplex? What does it look like? Let's draw some of these distributions - we can draw a maximum in three-dimensional space, so that the simplex will be two-dimensional - a triangle, in other words, and the distribution will be over this triangle (the picture is taken from here; in principle, it’s understandable what they are talking about, but it’s very interesting why Uniform (0,1) is signed under the Pandora’s mailbox - if anyone understands, tell me :)):
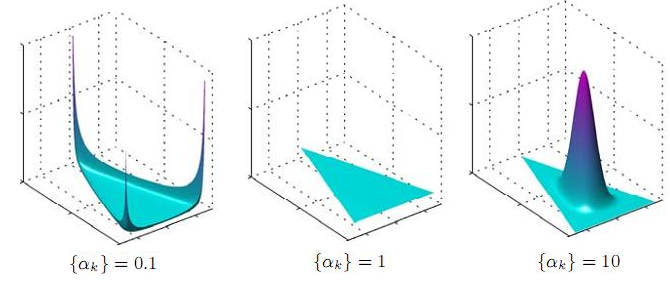
But the similar distributions are in two-dimensional format, in the form of heatmaps (how they can be drawn is explained, for example, here ); True, here 0.1 would be completely invisible, so I replaced it with 0.995:
And this is what happens: if α = 1, we get a uniform distribution (which is logical - then all degrees in the density function are equal to zero). If α is greater than unity, then with a further increase in α, the distribution is more and more concentrated in the center of the simplex. For large α, we will almost always get almost completely honest cubes. But the most interesting thing here is what happens when α is less than unity - in this case, the distribution focuses on the corners and edges / sides of the simplex! In other words, for small α we will get sparsecubes are distributions in which almost all probabilities are equal or close to zero, and only a small part of them are substantially nonzero. This is exactly what we need - and in the document we would like to see a few substantially expressed topics, and it would be nice to clearly outline the topic with a relatively small subset of words. Therefore, the LDA usually takes hyperparameters α and β less than unity, usually α = 1 / T (the inverse of the number of topics) and β = Const / W (a constant like 50 or 100 divided by the number of words).
Disclaimer: my presentation follows the simplest and most straightforward approach to LDA, I'm trying with large strokes to convey a general understanding of the model. In fact, of course, there are more detailed studies on how to choose the hyperparameters α and β, what they give and what lead to; in particular, hyperparameters do not have to be symmetrical at all. See, for example, Wallach, Nimho, McCallum's article “ Rethinking LDA: Why Priors Matter ”.
To summarize a brief summary. We have already explained all parts of the model - the a priori distribution of Dirichlet produces document cubes and topic bags, throwing a document dice determines its own theme for each word, and then the word itself is selected from the corresponding topic bag. Formally speaking, it turns out that the graphic model looks like this:
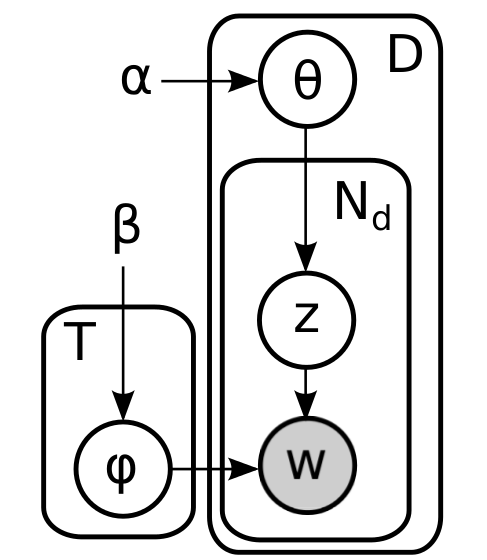
Here, the inner plate corresponds to the words of one document, and the outer plate corresponds to the documents in the case. No need to be fooled by the external simplicity of this picture, the cycles are more than enough here; here, for example, a fully expanded factor graph for two documents, one of which has two words, and the other three:
And the joint probability distribution, it turns out, is factorized like this:
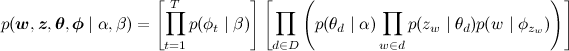
What is the task of teaching the LDA model now? It turns out that only words were given to us, nothing else was given, and we need to somehow teach all-all-all of these parameters. The task looks very scary - nothing is known and everything needs to be pulled out of a set of documents:
Nevertheless, it is solved using the very approximate output methods that we talked about earlier. Next time we’ll talk about how to solve this problem, apply the Gibbs sampling method (see one of the previous installations ) to the LDA model and derive the update equations for the variables z w ; we will see that in fact all this scary mathematics is not so scary at all, and the LDA is quite accessible to understanding not only conceptually, but also algorithmically.
LDA: intuition
So, we are starting a conversation about LDA. Let me remind you that the main goal of our generalization is to ensure that the document is not rigidly attached to one topic, and the words in the documents could come from several topics at once. What does this mean in (mathematical) reality? This means that the document is a mixture of topics, and each word can be generated from one of the topics in this mixture. Simply put, we first throw the document cube, determining the topic for each word , and then pull the word out of the corresponding bag.
Thus, the main intuition of the model looks something like this:
- in the world there are topics (previously unknown) that reflect what parts of the document might be about;
- each topic is a probability distribution in words, i.e. a bag of words from which you can pull out different words with different probability;
- each document is a mixture of topics, i.e. probability distribution on topics, a cube that can be thrown;
- the process of generating each word is to first select a topic by the distribution corresponding to the document, and then select a word from the distribution corresponding to this topic.
Since intuition is the most important thing, and here it is not the simplest, I will repeat again the same thing in other words, now a little more formally. Probabilistic models to understand and convenient to represent a generative process (generative processes), when we consistently describe how the data is generated by one unit, introducing therein all probability assumptions that we make in this model. Accordingly, the generating process for the LDA should consistently describe how we generate each word of each document. And this is how it happens (hereinafter I will assume that the length of each document is specified - it can also be added to the model, but usually it does not give anything new):
- for each topic t :
- choose a vector φ t (distribution of words in the topic) by distribution
;
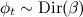- choose a vector φ t (distribution of words in the topic) by distribution
- for each document d :
- choose a vector 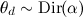- a vector of the "degree of expression" of each topic in this document;
- for each of the words in the document w :
- choose a theme z w by distribution
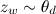; - choose a word
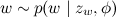with the probabilities given in β.
- choose a theme z w by distribution
- choose a vector
Here, the process of choosing a word for given θ and φ should already be clear to the reader - we throw a cube for each word and select the topic of the word, then we pull out the word itself from the corresponding bag:
In the model, it remains only to explain where these θ and φ come from and what means expression
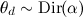; at the same time it will explain why this is called Dirichlet allocation.What does Dirichlet have to do with it?
Johann Peter Gustav Lejeune Dirichlet was not so much involved in probability theory; he mainly specialized in mathematics, number theory, Fourier series, and other similar mathematics. In probability theory, he was not so often seen, although, of course, his results in probability theory would have made a brilliant career for modern mathematics (trees were greener, sciences were less studied, and, in particular, mathematical Klondike was not exhausted either). However, in his studies of mathematical analysis, Dirichlet, in particular, managed to take such a classical integral, which as a result was called the Dirichlet integral:
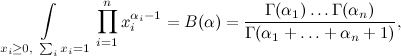
where Γ (α i ) is the gamma function, the continuation of the factorial (for natural numbers
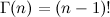) Dirichlet himself derived this integral for the needs of celestial mechanics, then Liouville found a simpler conclusion, which was generalized to more complex forms of integrands, and wrap it all up. The Dirichlet distribution motivated by the Dirichlet integral is the distribution on the ( n -1) -dimensional vector x 1 , x 2 , ..., x n -1 , defined in this way:
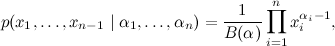
where
, and the distribution is given only on ( n -1) -dimensional simplex, where x i > 0. From it the Dirichlet integral a normalization constant appeared in it. And the meaning of the Dirichlet distribution is rather elegant - this is the distribution on the distributions. Look - as a result of sketching a vector over the Dirichlet distribution, we get a vector with non-negative elements, the sum of which is unity ... bah, but this is a discrete probability distribution, actually a dishonest cube with n faces. Of course, this is not the only possible class of distributions on discrete probabilities, but the Dirichlet distribution also has a number of other attractive properties. The main thing is that it is a conjugate a priori distribution for that very dishonest cube; I will not explain in detail what this means (possibly later), but, in general, it is reasonable to take the Dirichlet distribution as an a priori distribution in probabilistic models, when I want to get an unfair cube as a variable.
It remains to discuss what, in fact, will be obtained for different values of α i . First of all, let's just confine ourselves to the case when all α i are the same - we have a priori no reason to prefer some topics to others, at the beginning of the process we still don’t know where which topics will stand out. Therefore, our distribution will be symmetrical.
What does it mean - distribution on a simplex? What does it look like? Let's draw some of these distributions - we can draw a maximum in three-dimensional space, so that the simplex will be two-dimensional - a triangle, in other words, and the distribution will be over this triangle (the picture is taken from here; in principle, it’s understandable what they are talking about, but it’s very interesting why Uniform (0,1) is signed under the Pandora’s mailbox - if anyone understands, tell me :)):
But the similar distributions are in two-dimensional format, in the form of heatmaps (how they can be drawn is explained, for example, here ); True, here 0.1 would be completely invisible, so I replaced it with 0.995:
And this is what happens: if α = 1, we get a uniform distribution (which is logical - then all degrees in the density function are equal to zero). If α is greater than unity, then with a further increase in α, the distribution is more and more concentrated in the center of the simplex. For large α, we will almost always get almost completely honest cubes. But the most interesting thing here is what happens when α is less than unity - in this case, the distribution focuses on the corners and edges / sides of the simplex! In other words, for small α we will get sparsecubes are distributions in which almost all probabilities are equal or close to zero, and only a small part of them are substantially nonzero. This is exactly what we need - and in the document we would like to see a few substantially expressed topics, and it would be nice to clearly outline the topic with a relatively small subset of words. Therefore, the LDA usually takes hyperparameters α and β less than unity, usually α = 1 / T (the inverse of the number of topics) and β = Const / W (a constant like 50 or 100 divided by the number of words).
Disclaimer: my presentation follows the simplest and most straightforward approach to LDA, I'm trying with large strokes to convey a general understanding of the model. In fact, of course, there are more detailed studies on how to choose the hyperparameters α and β, what they give and what lead to; in particular, hyperparameters do not have to be symmetrical at all. See, for example, Wallach, Nimho, McCallum's article “ Rethinking LDA: Why Priors Matter ”.
LDA: graph, joint distribution, factorization
To summarize a brief summary. We have already explained all parts of the model - the a priori distribution of Dirichlet produces document cubes and topic bags, throwing a document dice determines its own theme for each word, and then the word itself is selected from the corresponding topic bag. Formally speaking, it turns out that the graphic model looks like this:
Here, the inner plate corresponds to the words of one document, and the outer plate corresponds to the documents in the case. No need to be fooled by the external simplicity of this picture, the cycles are more than enough here; here, for example, a fully expanded factor graph for two documents, one of which has two words, and the other three:
And the joint probability distribution, it turns out, is factorized like this:
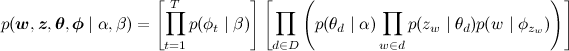
What is the task of teaching the LDA model now? It turns out that only words were given to us, nothing else was given, and we need to somehow teach all-all-all of these parameters. The task looks very scary - nothing is known and everything needs to be pulled out of a set of documents:
Nevertheless, it is solved using the very approximate output methods that we talked about earlier. Next time we’ll talk about how to solve this problem, apply the Gibbs sampling method (see one of the previous installations ) to the LDA model and derive the update equations for the variables z w ; we will see that in fact all this scary mathematics is not so scary at all, and the LDA is quite accessible to understanding not only conceptually, but also algorithmically.