Trivia of thinking or an article about dendritic spines
A few months ago a series of articles was published under the general title “Logic of Thinking” . Optimistically, it was planned to continue it in a month or two. But life has made its own adjustments. Modeling the pattern-wave model of the cortex gave such interesting results that I had to postpone everything else for a while, including writing a continuation of the cycle for the Habr.
However, not so long ago I wrote and posted an article on preprint ( http://arxiv.org/abs/1406.6901) In some ways, it may be interesting to those who were previously interested in the wave model. Let me remind you that the key point of the model is the statement that neurons are able to remember and recognize not only one image described by the weights of its synapses, but also a huge number of other signals different from this image. Of course, such a complication of a neuron runs counter to many existing theories and requires more than a serious justification. Below, I’ll just try to describe one of the arguments presented in the article in favor of my model.
This article should not be taken as a continuation of the cycle, it is rather a prequel to it. For myself, I called this the discussion of the key role of dendritic spines.
Let's start by repeating the well-known.
At rest between the internal and external environment of the neuron there is a potential difference - a membrane potential of about 70 millivolts. It is formed by protein molecules working like ion pumps. As a result, the membrane becomes polarized, in which a negative charge accumulates inside the cell, and a positive charge outside.
The surface of the neuron is covered with branching processes - dendrites. The axon endings of other neurons are adjacent to the body of the neuron and to its dendrites. The places of their connections are called synapses. Through synaptic interaction, a neuron is able to respond to incoming signals and, under certain circumstances, generate its own impulse, called a spike.
Signal transmission in synapses occurs due to the allocation of neurotransmitters. When a nerve impulse along the axon enters the presynaptic terminal, it releases neurotransmitter molecules characteristic of this synapse from synaptic vesicles. On the membrane of the neuron receiving the signal, receptors are located that interact with neurotransmitters.
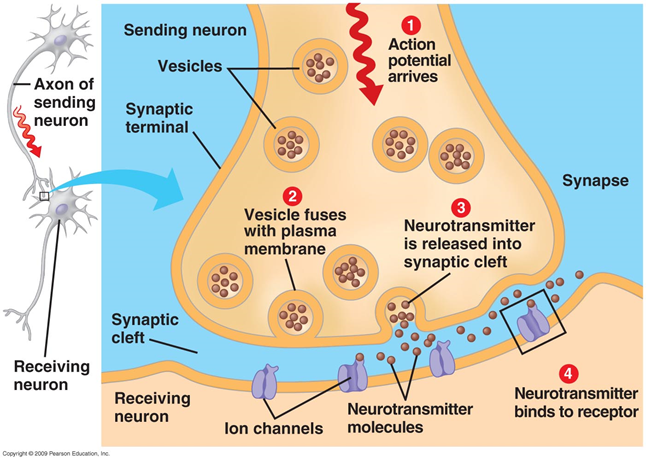
Figure 1. Chemical synapse
Receptors located in the synaptic cleft are mostly ionotropic. That is, they are ion channels, capable of transporting ions through the membrane of a neuron. Neurotransmitters act on receptors so that their ion channels open. As a result, the membrane is either depolarized or hyperpolarized, depending on which channels are affected and, accordingly, what type of synapse. In excitatory synapses, channels open, mainly passing cations into the cell, and the membrane is depolarized. In the inhibitory synapses, channels are opened that remove cations from the cell, which leads to hyperpolarization of the membrane.
In certain circumstances, synapses can change their sensitivity, which is called synaptic plasticity. This leads to the fact that some synapses become more, while others are less susceptible to external signals.
At the same time, a lot of signals arrive at the synapses of the neuron. The inhibitory synapses shift the membrane potential towards the accumulation of charge inside the cage. Activating synapses, on the contrary, try to discharge a neuron. When the total depolarization exceeds the initiation threshold, a discharge occurs, called the action potential or spike.
After the release of neurotransmitters, special mechanisms ensure their utilization and re-capture, which leads to the clearing of the synaptic cleft and the surrounding synapse space. During the refractory period following the spike, the neuron is not able to generate new impulses. The duration of this period determines the maximum generation frequency that a neuron is capable of.
Now we describe the facts less well-known.
When the action potential, propagating along the axon, reaches the recipient’s neuron, it causes the release of neurotransmitters into the synaptic cleft. These mediators determine the contribution of the synapse to the overall change in the membrane potential of the neuron receiving the signal. But some mediators fall outside the synaptic cleft and spreads over the space formed by neurons and glial cells surrounding them. This phenomenon is called spillover (spillover (English) - overflow, overflow) (Kullmann, 2000). In addition, neurotransmitters are emitted by non-synaptic axon terminals and glial cells (Figure 2). The concentration of neurotransmitters outside the synapses is much lower than in synaptic clefts. However, it is precisely in these “spreading” neurotransmitters that a lot of interesting things are hidden.
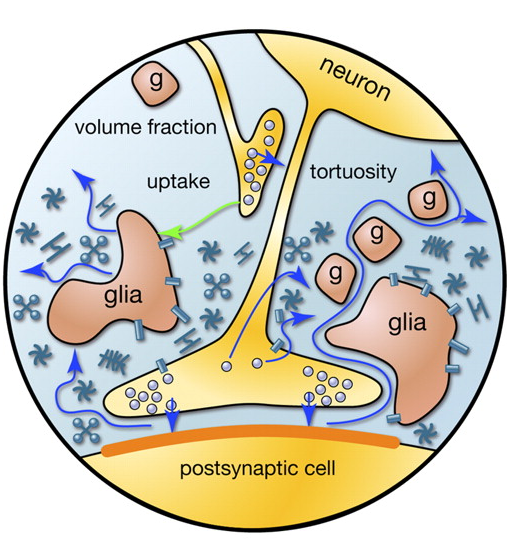
Figure 2. Sources of mediators outside the synaptic cleft (Sykova E., Mazel T., Vagrova L., Vorisek I., Prokopova-Kubinova S., 2000)
Let us try to estimate the number and structure of sources that throw neurotransmitters beyond the synapses. For this, we use the quantitative estimates of the parameters of the cortex given in the table below (Table 1) (Braitenberg V., Schuz A., 1998).
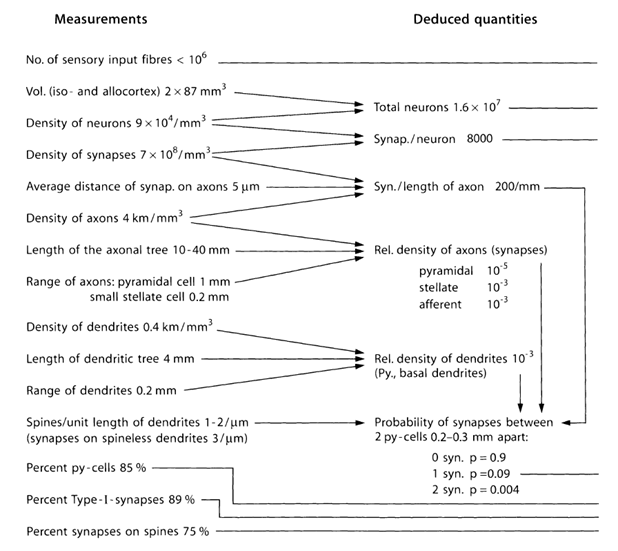
Table 1. A summary table of parameters obtained in the study of the mouse brain (py-cell - a pyramidal cell, Type-I - synapses between two pyramidal cells) (Braitenberg V., Schuz A., 1998)
Let me remind you that most of the synapses (90-95%) do not fall on the body of the neuron, but on its dendrites. Dendrites are thin branching processes that form the so-called dendritic tree of a neuron. In the figures below, dendritic trees are highlighted in black and axons in gray. For neurons of different types, the forms of dendritic trees are different, but the general principle remains: the dendritic tree consists of many branching processes, while the greatest density of synaptic connections of the neuron falls on a small spatial region. For the main types of neurons, it is about 200 μm (Figure 3, Figure 4).

Figure 3. Structure of a stellate neuron, ruler - 0.1 mm (Braitenberg, 1978)
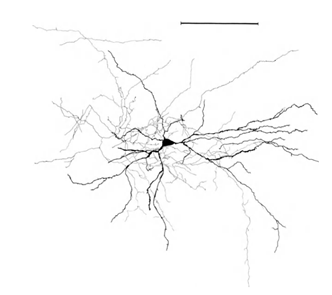
Figure 4. Structure of a pyramidal neuron, ruler - 0.1 mm (Braitenberg, 1978)
Branching axons of neurons form contacts (synapses) with dendrites of other neurons. The average distance between synapses on dendrites is 0.5 micrometers. The average distance between synapses on axons is 5 micrometers, that is, 10 times more. Not surprisingly, axons are about 10 times longer than dendrites.
Most (75%) synapses are located on dendritic spines, which is most characteristic of pyramidal cells (Figure 5).
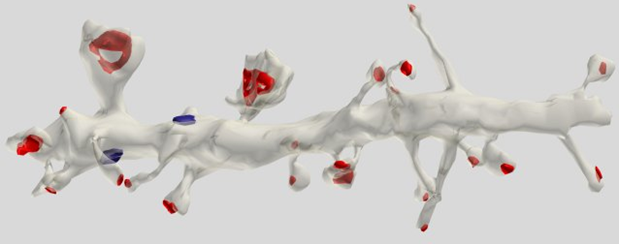
Figure 5. The dendrite segment of the pyramidal cell. The red synapses are marked on the spines, the blue - on the dendritic trunk (Dr. Kristen M. Harris)
Computer simulation based on real anatomical and physiological data showed that, for example, glutamate can spread beyond the synaptic cleft in quantities sufficient to activate NMDA receptors in a radius comparable to the distance between adjacent synapses (0.5 μm) (Rusakov DA, Kullmann DM, 1998). It can be assumed that a significant concentration of neurotransmitters after spilover is observed in the area of the dendrite about 1-2 μm long. On such a site, about two to four synapses belonging to this dendrite can be located.
If we take a section of dendrite 5 μm long (Figure 6), then the expected number of synapses on it will be about 10.
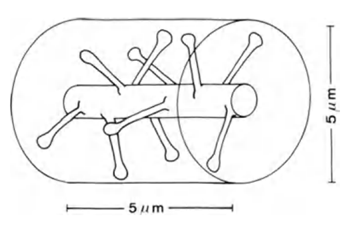
Figure 6. Section of a dendrite (Braitenberg V., Schuz A., 1998)
But dendritic branches of some neurons are closely intertwined with branches of other neurons. They pass from each other in the immediate vicinity. Due to the height of the dendritic spines, synapses belonging to one dendrite may be closer to the surface of another dendrite than its own synapses.
If the synapses were evenly distributed in the cortical space, then into a cylindrical volume 5 μm high and also 5 μm in diameter (figure above) with a synapse distribution density of 7x10 8 / mm 3about 100 synapses would hit. That is, 10 times more than what is directly located on the branch itself. In fact, a significant part of the volume of the brain is occupied by glial cells and the bodies of neurons, which further increases the packing density of synapses. However, neurons work with different neurotransmitters, which also needs to be taken into account.
Now let's try to understand the meaning of such a structure of bonds from the point of view of the density distribution of the extrasynaptic mediator. For this we use a simplified model. Take the conditional volume surrounding the neuron and number the neurons entering it. Each of these neurons will have:
• several synaptic contacts with the dendrite of the selected neuron;
• several “fits”, that is, places where its synapses with other neurons will be located in close proximity to the dendrite of the selected neuron.
Let us imagine a dendritic tree as one long branch with evenly distributed conditional sources (Figure 7). For each source on this branch, you can specify the number of the neuron from the surrounding space responsible for it. Each of the surrounding neurons will have several source contacts at once, randomly distributed over the dendrite. Denote this correlation by the vector D with elements d i .

Figure 7. Correlation of surrounding neurons and their contacts on the dendrite.
We introduce the following notation:
N neuron - number of environmental neurons
N source- the number of sources for one neuron
N trap - the number of sources that create the density level of neurotransmitters (synaptic trap)
Now suppose that several neurons from the environment gave a spike. This can be perceived as a signal available for observation to our neuron. Denote N sig - the number of active neurons that create the information signal. We write this signal as binary vector S.
For all positions on the dendrite except the most extreme, we will consider the mediator density according to the formula

For example, for the signal shown in the figure below, the density in the marked synaptic trap will be 2 (the sum of signals from the 1st and 4th neurons )
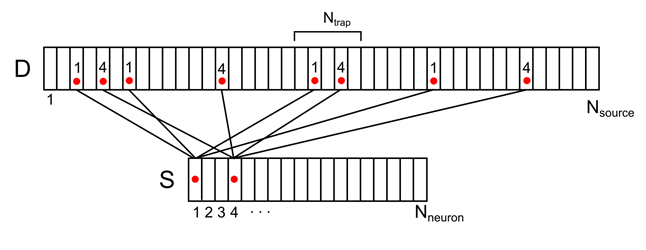
Figure 8. Mapping of the activity of two environmental neurons onto a dendritic tree (only a part of the connections and numbering is shown)
For any arbitrary signal, the density pattern of mediators on the dendrite can be calculated. This density will range from 0 to N trap . The maximum value will be achieved if all sources forming a synaptic trap are active.
We use the average values of the parameters characteristic of the real rat cortex (Braitenberg V., Schuz A., 1998). Based on them, we obtain the following model parameters:
N neuron = 650
N source = 25000
N trap = 15
We assume that the signal is encoded by activity, for example, 1.5% of cortical neurons, then
N sig = 10
It is easy to calculate the probability that for an arbitrary signal consisting of N sig units, there will be at least one place on the dendrite where the mediator density will be exactly K . For the given parameters, the probability takes the following values (Table 2):
| K | P |
| 0 | 0.984 |
| one | one |
| 2 | one |
| 3 | 0,996 |
| four | 0.287 |
| five | 0.016 |
| 6 | 0.001 |
| 7 | 0 |
| eight | 0 |
| 9 | 0 |
| ten | 0 |
| ... |
Table 2. The probability table for finding at least one trap with a given density. The first column is the required number of active sources in the trap. The second is the probability of finding at least one place on the dendrite where exactly such a number of active sources will be.
That is, for parameters that are close to the configuration of the real cortex, for any volume signal affecting about 1.5% of neurons, the following is true:
• There will be about 1.6 % of neurons that have a trap on dendrites where 50% of signal axons intersect;
• Almost every neuron has traps in which at least 30% of the signal axons intersect.
The meaning of this result is very interesting. Suppose that the information in the cortex is somehow encoded by the synchronous activity of a relatively small number (N sig ) of compactly located neurons. This is not about all the activity of the brain, but about information processes in a small volume, where neurons are numbered by us from 1 to N neuron . Suppose that the number of code combinations S is limited and forms a certain dictionary T with a capacity of N dict . It is possible to calculate the probability that the same place will “respond” to two signals at once. The results of such a calculation for a dictionary of 10,000 signals in the table below.
| K | P error |
| 3 | 0.00399 |
| four | 1,05E-05 |
| five | 1.89E-08 |
| 6 | 2,33E-11 |
| 7 | 0 |
| ... |
Table 3. The probability table of violation of the uniqueness of the synaptic trap at various levels of mediator density
It turns out that at K = 3 the traps have a certain selectivity, although they do not guarantee error, but already at K = 5 they begin to quite unambiguously correspond to a certain spatial activity pattern. Let me remind you that this is not true for arbitrary signals from an infinite set, but when we have a set, albeit a sufficiently large, of discrete allowed states of activity.
That is, it turns out that the meaning of the structure of axon and dendritic trees characteristic of the brain is to create a rich space of traps on the dendritic surface of each neuron, that is, places corresponding to all kinds of combinations of sources of neurotransmitters. By the density of the neurotransmitter in the traps, one can judge the spatially distributed signal, which is the sum of the synchronous activity of a number of nearby neurons.
And since the so-called metabotropic receptors are located on the surface of the neuron, which can cause single neuron spikes even at low concentrations of neurotransmitters, it turns out that these spikes, which are called spontaneous, can respond to a huge number of different signals, different from those to which neuron synapses can be tuned.
Actually, now we can explain the purpose of the very dendritic spines with which the article began. In theory, all synapses could be located directly on the dendrite or body of the neuron. This would not affect the direct work of synapses and their ability to contribute to the appearance of induced activity. But now we can assume that the appointment of dendritic spines is the creation of a spatial structure in which the synapses of different neurons are “mixed” so that they acquire the ability with their spilover to influence not only their surface, but also the surrounding neighboring dendrites. Such a “trifle in principle” is obtained.
The original article shows how the “wave history” itself is born out of this, but this is a separate conversation.
And in conclusion, a little self-interest. Original article in original in Russian. There is a translation into English made by Dmitry Shabanov (for which he has a huge respect), but he (translation) is far from perfect. If anyone has the opportunity to look and point out the mistakes, I will be extremely grateful. The document by reference is open to everyone for comment.
References to the original article
1. (2014). Retrieved from the Human Connectome Project: www.humanconnectomeproject.org
2. (2014). Retrieved from ALLEN Mouse Brain Connectivity Atlas: connectivity.brain-map.org
3. Bloom, BH (1970). Space / time trade-offs in hash coding with allowable errors. Communications of the ACM T. 13 (7), 422-426.
4. Braitenberg V., Schuz A. (1998). Cortex: statistics and geometry of neuronal connectivity, 2nd ed.
5. Braitenberg, V. (1978). Cortical architectonics: general and areal. In MAB Brazier and H. Petsche (eds), Architectonics of the Cerebral Cortex (pp. 443–465). New York: Raven Press.
6. Coster, H. (1975). Electromechanical stresses and the effect of pH on membrane structure. Biochim Biophys Acta 13; 382 (2), 142-146.
7. Dr. Kristen M. Harris. (bd). Synapse Web. Retrieved from synapses.clm.utexas.edu .
8. Fukushima, K. (1980). Neocognitron A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biological Cybernetics, 36 (4), 193-202.
9. Grossberg, S. (1987). Competitive learning: From interactive activation to adaptive resonance. Cognitive Science N11, 23-63.
10. Hebb, D. (1949). The Organization of Behavior. New York: John Wiley & Sons.
11. Hodgkin, A. a. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve ... J. Physio l. 117, 500-544.
12. Izhikevich, EM (2007). Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. London: The MIT Press.
13. Kullmann, DM (2000). Spillover and synaptic cross talk mediated by glutamate and GABA in the mammalian brain. Prog Brain Res, 125, 339-351.
14. Kuramoto, Y. (1984). Chemical Oscillations, Waves, and Turbulence. Dover Publications.
15. Liibke J., Markram H., Frotscher M., Sakmann B. (1996). Frequency and dendritic distribution bution of autapses established by layer 5 pyramidal neurons in the developing rat neocortex: comparisons with synaptic innervation of adjacent neurons of the same class. Neurosci 16 (10), 3209-3218.
16. Malenka RC, Nicoll RA (1999). Long-term potentiation - a decade of progress? Science 285 (5435), 1870-1874.
17. Michael T. Lippert, Kentaroh Takagaki, Weifeng Xu, Xiaoying Huang, Jian-Young Wu. (2007). Methods for Voltage-Sensitive Dye Imaging of Rat Cortical Activity With. J Neurophysiol 98, 502-512.
18. Pitts W., McCulloch WS (1947). How we know universals: the perception of auditory and visual forms. Bull. Math. Biophys V. 9, 127-147.
19. Rosenblatt, F. (1962). Principles of Neurodynamic: Perceptrons and the Theory of Brain Mechanisms.
20. Rusakov DA, Kullmann DM (1998). Extrasynaptic glutamate diffusion in the hippocampus: ultrastructural constraints, uptake, and receptor activation. Neurosci 18 (9), 3158-3170.
21. Sheng, M., Nakagawa, T. (2002). Neurobiology: glutamate receptors on the move. Nature, 417 (6889), 601-602.
22. Sheng, M., Sala C. (2001). PDZ domains and the organization of supramolecular complexes. Annu Rev Neurosci, 24, 1-29.
23. Sykova E., Mazel T., Vagrova L., Vorisek I., Prokopova-Kubinova S. (2000). Extracellular space diffusion and pathological states. Progress in Brain Research, 155-178.
24. Tovar KR, Westbrook GL (2002). Mobile NMDA receptors at hippocampal synapses. Neuron, 34 (2), 255-264.
25. W.-F. Xu, X.-Y. Huang, K. Takagaki, and J.-Y. Wu (2007). Compression and reflection of visually evoked cortical waves. Neuron, 55, 119-129.
26. Y. LeCun, Y. Bengio. (1995). Convolutional Networks for Images, Speech, and Time-Series, in Arbib, MA, editor, The Handbook of Brain Theory and Neural Networks. MIT Press.
27. J.P. Shnurova, Z.M. Gvozdikova. (1971). The reaction of neurons in the sensorimotor region of the cortex to its direct electrical stimulation. In the collection "Research on the organization of neural activity of the cerebral cortex" (p. 158-180). Moscow: Science.
28. Nicholls J., Martin R., Wallas B., Fuchs P. (2003). From Nero to the Brain (fourth edition).
29. Pribram, K. (1971). Languages of the brain.
30. Radchenko, A.N. (2007). Information mechanisms of the brain. SPb
31. Redozubov, A. (2014). A program for calculating the distribution of synaptic traps. Retrieved from aboutbrain.ru: www.aboutbrain.ru/programs
32. Redozubov, A. (2014). Wave cortex simulation program. Retrieved from aboutbrain.ru: www.aboutbrain.ru/programs
