Amazon SQS Testing
The network already has several reviews of the performance of this solution from Amazon, in this article I did not pursue the goal of checking the results already obtained, I was interested in some features that are not considered in other sources, namely:
The most supported library for AWS on erlang is erlcloud [1], to initialize the library, just call the start and configure methods, as indicated on github. My messages will contain a random character set generated by the following function:
for speed measurements, we will use the well-known function that uses timer: tc, but with some changes:
the changes relate to the call of the function under test, in this version I added the R argument, which allows us to use the value returned at the previous start, this is necessary in order to generate message numbers and collect additional information regarding shuffling when receiving a message. Thus, the function of sending a message with a number will look like this:
And her call with statistics collection:
here 31 is the number of the first message, this number was not chosen by chance, the fact is that erlang does not distinguish between sequences of numbers and strings very well and in the message it will be character number 31, lower numbers can be transmitted to SQS, but continuous ranges in this case are obtained small (# x9 | #xA | #xD | [# x20 to # xD7FF] | [# xE000 to #xFFFD] | [# x10000 to # x10FFFF], more details [2]) and you will get an exception when you leave the valid range. Thus, the send_random function generates and sends a message to the queue with the name Queue, at the beginning of which there is a number that determines its number, the function returns the number of the next number, which is used further by the next generation function. The test_avg function takes a QueueName, which becomes the second argument to the send_random function, the first argument is the number and number of repetitions.
The function that will receive messages and check their order will look like this:
Delete messages:
the list sent for deletion contains a lot of extra information (message body, etc.), the deletion function finds receipt_handle, which is required to form a request, or returns wrong if receipt_handle is not found
Looking ahead, I can say that even with a small number of messages the mixing turned out to be quite significant and an additional problem arose: it is necessary to evaluate the degree of mixing. Unfortunately, no good criteria were found and it was decided to derive the maximum and average discrepancy with the correct position. Knowing the size of such a window, it is possible to restore the order of messages upon receipt, while, of course, the processing speed deteriorates.
To calculate such a difference, it is enough to change only the message order checking function:
the call to the series execution function will look like this:
I get the number of elements that came later than necessary, the sum of their distances from the largest of the received elements and the maximum offset. The most interesting thing for me here is the maximum bias, the other characteristics can be called controversial and they may not be calculated very well (for example, if one element is read earlier, then all the elements that must go before it will be considered rearranged in this case). To the results:
The first line is the number of messages in the queue, the second is the maximum offset, the third is the average offset.
The results surprised me, the messages do not just mix, this simply has no boundaries, that is, with an increase in the number of messages, the size of the window being viewed needs to be increased. The same in graph form:
As I already wrote, Amazon SQS does not support subscriptions, Amazon SNS can be used for this, but if fast queues with several handlers are required, this is not suitable, in order not to pull the message receiving method Amazon implemented Long Polling, which allows you to hang around waiting for a message up to twenty seconds, and since SQS is charged by the number of called methods this should significantly reduce queue costs, but here's the problem: for a small number of messages (according to official documentation), the queue may not be returned nothing. This behavior is critical for queues in which you need to quickly respond to an event, and generally speaking, if this happens often then Long Polling does not make much sense, since it becomes equivalent to periodic polls with SQS reaction times.
For verification, we will create two processes, one of which will send messages at random times, and the second will always be in Long Polling, while the moments of sending and receiving messages will be saved for later comparison. In order to enable this mode, set Receive Message Wait Time = 20 seconds in the queue parameters.
this function falls asleep for a random number of milliseconds, after which it remembers the moment and sends a message
these two functions allow you to receive messages and remember the moments at which this happened. After the simultaneous execution of these functions with spawn, I get two lists, the difference between which shows the reaction time to the message. It does not take into account the fact that messages can be mixed, in general, this will simply increase the reaction time additionally.
Let's see what happened:
the first line is the value set as the maximum delay of the sending process. That is: 10 seconds, 7.5 seconds ... The remaining lines are the minimum, maximum and average time to wait for a message.
The same in the form of a graph: The

average time was the same in all cases, we can say that on average two seconds elapse between sending such single messages. Long enough. In this test, the sample was quite small, 20 messages, so the minimum-maximum values are more a matter of luck than some kind of dependency.
First, let’s check how important the effect of “warming up” the queue when sending messages is:
The same is in the form of a graph:

we can say that no heating is observed, that is, the queue behaves approximately the same on these volumes of data, for some reason the maximum increases, but the average and minimum remain in their places.
Same for read with delete

There is also no saturation, the average is around 200ms. Sometimes reading occurred instantly (faster than 1 ms), but this means that the message was not received, according to the documentation, SQS servers can do this, you just need to request the message again.
We will proceed directly to the block and multi-threaded testing
. Unfortunately, the erlcloud library does not contain functions for batch sending messages, but such functions are not difficult to implement on the basis of existing ones;
and add the function of forming the request:
The library should also fix the API version, for example, on 2011-10-01, otherwise Amazon will return a Bad request in response to your requests.
testing functions are similar to those used in other tests:
Here we just had to change the length of the messages so that the whole package fit into 64kb, otherwise an exception is thrown.
The following data was obtained for recording:
here 0 means reading one by one in 1 stream, then 1 reading by 10 into 1 stream, 10 into 2 streams, 10 into 4 streams and so on
To read:
graph reflecting the bandwidth for reading and writing (messages per second):

Blue - writing, red - reading.
From this data it can be concluded that the maximum throughput is achieved for writing in the region of 10 streams, and for reading - about 50, with a further increase in the number of streams, the number of messages sent per unit time does not increase.
It turns out that Amazon SQS significantly changes the order of messages, has not too good response time and throughput, you can only counter this with reliability and a small (in case of a small number of messages) fee. That is, if speed is not critical to you, it does not matter that the messages are mixed up and you do not want to administer or hire a queue server administrator - this is your choice.
- the documentation says Amazon is trying to keep the message order, how well is it stored?
- How fast is receiving a message when using Long Polling?
- How much does batch processing speed up?
Formulation of the problem
The most supported library for AWS on erlang is erlcloud [1], to initialize the library, just call the start and configure methods, as indicated on github. My messages will contain a random character set generated by the following function:
random_string(0) -> [];
random_string(Length) -> [random_char() | random_string(Length-1)].
random_char() -> random:uniform(95) + 31 .
for speed measurements, we will use the well-known function that uses timer: tc, but with some changes:
test_avg(M, F, A, R, N) when N > 0 ->
{Ret, L} = test_loop(M, F, A, R, N, []),
Length = length(L),
Min = lists:min(L),
Max = lists:max(L),
Med = lists:nth(round((Length / 2)), lists:sort(L)),
Avg = round(lists:foldl(fun(X, Sum) -> X + Sum end, 0, L) / Length),
io:format("Range: ~b - ~b mics~n"
"Median: ~b mics~n"
"Average: ~b mics~n",
[Min, Max, Med, Avg]),
Ret.
test_loop(_M, _F, _A, R, 0, List) ->
{R, List};
test_loop(M, F, A, R, N, List) ->
{T, Result} = timer:tc(M, F, [R|A]),
test_loop(M, F, A, Result, N - 1, [T|List]).
the changes relate to the call of the function under test, in this version I added the R argument, which allows us to use the value returned at the previous start, this is necessary in order to generate message numbers and collect additional information regarding shuffling when receiving a message. Thus, the function of sending a message with a number will look like this:
send_random(N, Queue) ->
erlcloud_sqs:send_message(Queue, [N + 1 | random_string(6000 + random:uniform(6000))]),
N + 1 .
And her call with statistics collection:
test_avg(?MODULE, send_random, [QueueName], 31, 20)
here 31 is the number of the first message, this number was not chosen by chance, the fact is that erlang does not distinguish between sequences of numbers and strings very well and in the message it will be character number 31, lower numbers can be transmitted to SQS, but continuous ranges in this case are obtained small (# x9 | #xA | #xD | [# x20 to # xD7FF] | [# xE000 to #xFFFD] | [# x10000 to # x10FFFF], more details [2]) and you will get an exception when you leave the valid range. Thus, the send_random function generates and sends a message to the queue with the name Queue, at the beginning of which there is a number that determines its number, the function returns the number of the next number, which is used further by the next generation function. The test_avg function takes a QueueName, which becomes the second argument to the send_random function, the first argument is the number and number of repetitions.
The function that will receive messages and check their order will look like this:
checkorder(N, []) -> N;
checkorder(N, [H | T]) ->
[{body, [M | _]}|_] = H,
K = if M > N -> M;
true -> io:format("Wrong ~b less than ~b~n", [M, N]),
N
end,
checkorder(K, T).
receive_checkorder(LastN, Queue) ->
[{messages, List} | _] = erlcloud_sqs:receive_message(Queue),
remove_list(Queue, List),
checkorder(LastN, List).
Delete messages:
remove_msg(_, []) -> wrong;
remove_msg(Q, [{receipt_handle, Handle} | _]) -> erlcloud_sqs:delete_message(Q, Handle);
remove_msg(Q, [_ | T]) -> remove_msg(Q, T).
remove_list(_, []) -> ok;
remove_list(Q, [H | T]) -> remove_msg(Q, H), remove_list(Q, T).
the list sent for deletion contains a lot of extra information (message body, etc.), the deletion function finds receipt_handle, which is required to form a request, or returns wrong if receipt_handle is not found
Mixing messages
Looking ahead, I can say that even with a small number of messages the mixing turned out to be quite significant and an additional problem arose: it is necessary to evaluate the degree of mixing. Unfortunately, no good criteria were found and it was decided to derive the maximum and average discrepancy with the correct position. Knowing the size of such a window, it is possible to restore the order of messages upon receipt, while, of course, the processing speed deteriorates.
To calculate such a difference, it is enough to change only the message order checking function:
checkorder(N, []) -> N;
checkorder({N, Cnt, Sum, Max}, [H | T]) ->
[{body, [M | _]}|_] = H,
{N1, Cnt1, Sum1, Max1} = if M < N ->
{N, Cnt + 1, Sum + N - M, if Max < N - M -> N - M; true -> Max end };
true -> {M, Cnt, Sum, Max}
end,
checkorder({N1, Cnt1, Sum1, Max1}, T).
the call to the series execution function will look like this:
{_, Cnt, Sum, Max} = test_avg(?MODULE, receive_checkorder, [QueueName], {0, 0, 0, 0}, Size)
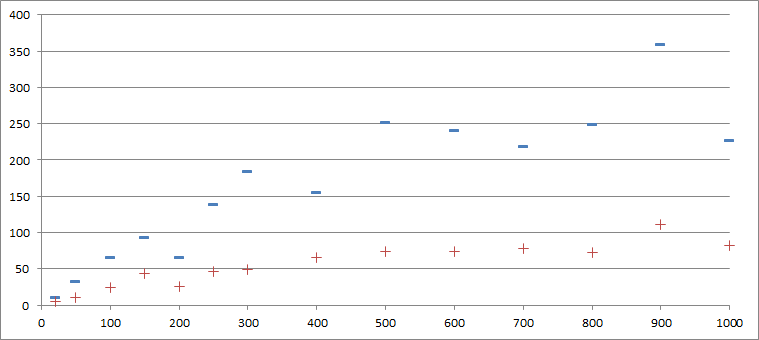
I get the number of elements that came later than necessary, the sum of their distances from the largest of the received elements and the maximum offset. The most interesting thing for me here is the maximum bias, the other characteristics can be called controversial and they may not be calculated very well (for example, if one element is read earlier, then all the elements that must go before it will be considered rearranged in this case). To the results:
| Size (pcs) | 20 | fifty | 100 | 150 | 200 | 250 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Maximum Offset (pcs) | eleven | 32 | 66 | 93 | 65 | 139 | 184 | 155 | 251 | 241 | 218 | 249 | 359 | 227 |
| The average displacement (pcs) | 5.3 | 10.5 | 23.9 | 43 | 25.6 | 45.9 | 48.4 | 65.6 | 74.2 | 74.2 | 78.3 | 72.3 | 110.8 | 82.8 |
The first line is the number of messages in the queue, the second is the maximum offset, the third is the average offset.
The results surprised me, the messages do not just mix, this simply has no boundaries, that is, with an increase in the number of messages, the size of the window being viewed needs to be increased. The same in graph form:

Long polling
As I already wrote, Amazon SQS does not support subscriptions, Amazon SNS can be used for this, but if fast queues with several handlers are required, this is not suitable, in order not to pull the message receiving method Amazon implemented Long Polling, which allows you to hang around waiting for a message up to twenty seconds, and since SQS is charged by the number of called methods this should significantly reduce queue costs, but here's the problem: for a small number of messages (according to official documentation), the queue may not be returned nothing. This behavior is critical for queues in which you need to quickly respond to an event, and generally speaking, if this happens often then Long Polling does not make much sense, since it becomes equivalent to periodic polls with SQS reaction times.
For verification, we will create two processes, one of which will send messages at random times, and the second will always be in Long Polling, while the moments of sending and receiving messages will be saved for later comparison. In order to enable this mode, set Receive Message Wait Time = 20 seconds in the queue parameters.
send_sleep(L, Queue) ->
timer:sleep(random:uniform(10000)),
Call = erlang:now(),
erlcloud_sqs:send_message(Queue, random_string(6000 + random:uniform(6000))),
[Call | L].
this function falls asleep for a random number of milliseconds, after which it remembers the moment and sends a message
remember_moment(L, []) -> L;
remember_moment(L, [_ | _]) -> [erlang:now() | L].
receive_polling(L, Queue) ->
[{messages, List} | _] = erlcloud_sqs:receive_message(Queue),
remove_list(Queue, List),
remember_moment(L, List).
these two functions allow you to receive messages and remember the moments at which this happened. After the simultaneous execution of these functions with spawn, I get two lists, the difference between which shows the reaction time to the message. It does not take into account the fact that messages can be mixed, in general, this will simply increase the reaction time additionally.
Let's see what happened:
| Sleep interval | 10,000 | 7500 | 5000 | 2500 |
|---|---|---|---|---|
| Minimum time (sec) | 0.27 | 0.28 | 0.27 | 0.66 |
| Maximum time (sec) | 10.25 | 7.8 | 5.36 | 5.53 |
| Average time (sec) | 1.87 | 1.87 | 1.84 | 1.88 |
the first line is the value set as the maximum delay of the sending process. That is: 10 seconds, 7.5 seconds ... The remaining lines are the minimum, maximum and average time to wait for a message.
The same in the form of a graph: The

average time was the same in all cases, we can say that on average two seconds elapse between sending such single messages. Long enough. In this test, the sample was quite small, 20 messages, so the minimum-maximum values are more a matter of luck than some kind of dependency.
Batch sending
First, let’s check how important the effect of “warming up” the queue when sending messages is:
| Number of records | 20 | fifty | 100 | 150 | 200 | 250 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Minimum time (sec) | 0.1 | 0.1 | 0.1 | 0.09 | 0.09 | 0.09 | 0.09 | 0.1 | 0.09 | 0.1 | 0.1 | 0.09 | 0.09 | 0.09 |
| Maximum time (sec) | 0.19 | 0.37 | 0.41 | 0.41 | 0.37 | 0.38 | 0.37 | 0.43 | 0.39 | 0.66 | 0.74 | 0.48 | 0.53 | 0.77 |
| Average time (sec) | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 |
The same is in the form of a graph:

we can say that no heating is observed, that is, the queue behaves approximately the same on these volumes of data, for some reason the maximum increases, but the average and minimum remain in their places.
Same for read with delete
| Number of records | 20 | fifty | 100 | 150 | 200 | 250 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Minimum time (sec) | 0.001 | 0.14 | 0 | 0.135 | 0 | 0.135 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Maximum time (sec) | 0.72 | 0.47 | 0.65 | 0.65 | 0.69 | 0.51 | 0.75 | 0.75 | 0.76 | 0.73 | 0.82 | 0.79 | 0.74 | 0.91 |
| Average time (sec) | 0.23 | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | 0.2 | 0.2 | 0.2 | 0.2 | 0.21 |

There is also no saturation, the average is around 200ms. Sometimes reading occurred instantly (faster than 1 ms), but this means that the message was not received, according to the documentation, SQS servers can do this, you just need to request the message again.
We will proceed directly to the block and multi-threaded testing
. Unfortunately, the erlcloud library does not contain functions for batch sending messages, but such functions are not difficult to implement on the basis of existing ones;
Doc = sqs_xml_request(Config, QueueName, "SendMessageBatch",
encode_message_list(Messages, 1)),
and add the function of forming the request:
encode_message_list([], _) -> [];
encode_message_list([H | T], N) ->
MesssageId = string:concat("SendMessageBatchRequestEntry.", integer_to_list(N)),
[{string:concat(MesssageId, ".Id"), integer_to_list(N)}, {string:concat(MesssageId, ".MessageBody"), H} | encode_message_list(T, N + 1)].
The library should also fix the API version, for example, on 2011-10-01, otherwise Amazon will return a Bad request in response to your requests.
testing functions are similar to those used in other tests:
gen_messages(0) -> [];
gen_messages(N) -> [random_string(5000 + random:uniform(1000)) | gen_messages(N - 1)].
send_batch(N, Queue) ->
erlang:display(erlcloud_sqs:send_message_batch(Queue, gen_messages(10))),
N + 1 .
Here we just had to change the length of the messages so that the whole package fit into 64kb, otherwise an exception is thrown.
The following data was obtained for recording:
| Number of threads | 0 | 1 | 2 | 4 | 5 | 10 | 20 | fifty | 100 |
|---|---|---|---|---|---|---|---|---|---|
| Maximum delay (sec) | 0.452 | 0.761 | 0.858 | 1.464 | 1.698 | 3.14 | 5.272 | 11.793 | 20.215 |
| Average delay (sec) | 0.118 | 0.48 | 0.436 | 0.652 | 0.784 | 1.524 | 3.178 | 9.1 | 19.889 |
| Message Time (sec) | 0.118 | 0.048 | 0.022 | 0.017 | 0.016 | 0.016 | 0.017 | 0.019 | 0.02 |
here 0 means reading one by one in 1 stream, then 1 reading by 10 into 1 stream, 10 into 2 streams, 10 into 4 streams and so on
To read:
| Number of threads | 0 | 1 | 2 | 4 | 5 | 10 | 20 | fifty | 100 |
|---|---|---|---|---|---|---|---|---|---|
| Maximum delay (sec) | 0.762 | 2.998 | 2.511 | 2.4 | 2.606 | 2.751 | 4.944 | 11.653 | 18.517 |
| Average delay (sec) | 0.205 | 1.256 | 1.528 | 1.566 | 1.532 | 1.87 | 3.377 | 7.823 | 17.786 |
| Message Time (sec) | 0.205 | 0.126 | 0.077 | 0.04 | 0.031 | 0.02 | 0.019 | 0.017 | 0.019 |
graph reflecting the bandwidth for reading and writing (messages per second):

Blue - writing, red - reading.
From this data it can be concluded that the maximum throughput is achieved for writing in the region of 10 streams, and for reading - about 50, with a further increase in the number of streams, the number of messages sent per unit time does not increase.
conclusions
It turns out that Amazon SQS significantly changes the order of messages, has not too good response time and throughput, you can only counter this with reliability and a small (in case of a small number of messages) fee. That is, if speed is not critical to you, it does not matter that the messages are mixed up and you do not want to administer or hire a queue server administrator - this is your choice.
References
- Erlcloud on github github.com/gleber/erlcloud
- www.w3.org/TR/REC-xml/#charsets
