Digit frequency analysis in MD5 hash
We all know what a hash looks like, but have you ever wondered how often a particular character is found in a hash? I wondered. And I decided to check. Sketched a Python script to count, and here's what came of it.
First, I generated a random string of characters (length from 0 to 1000).
Next, I took the MD5 hash from the string.
After - I calculated how many digits from 0 to 9 are in the hash. On a sample of 1000 hashes, I received the following data:
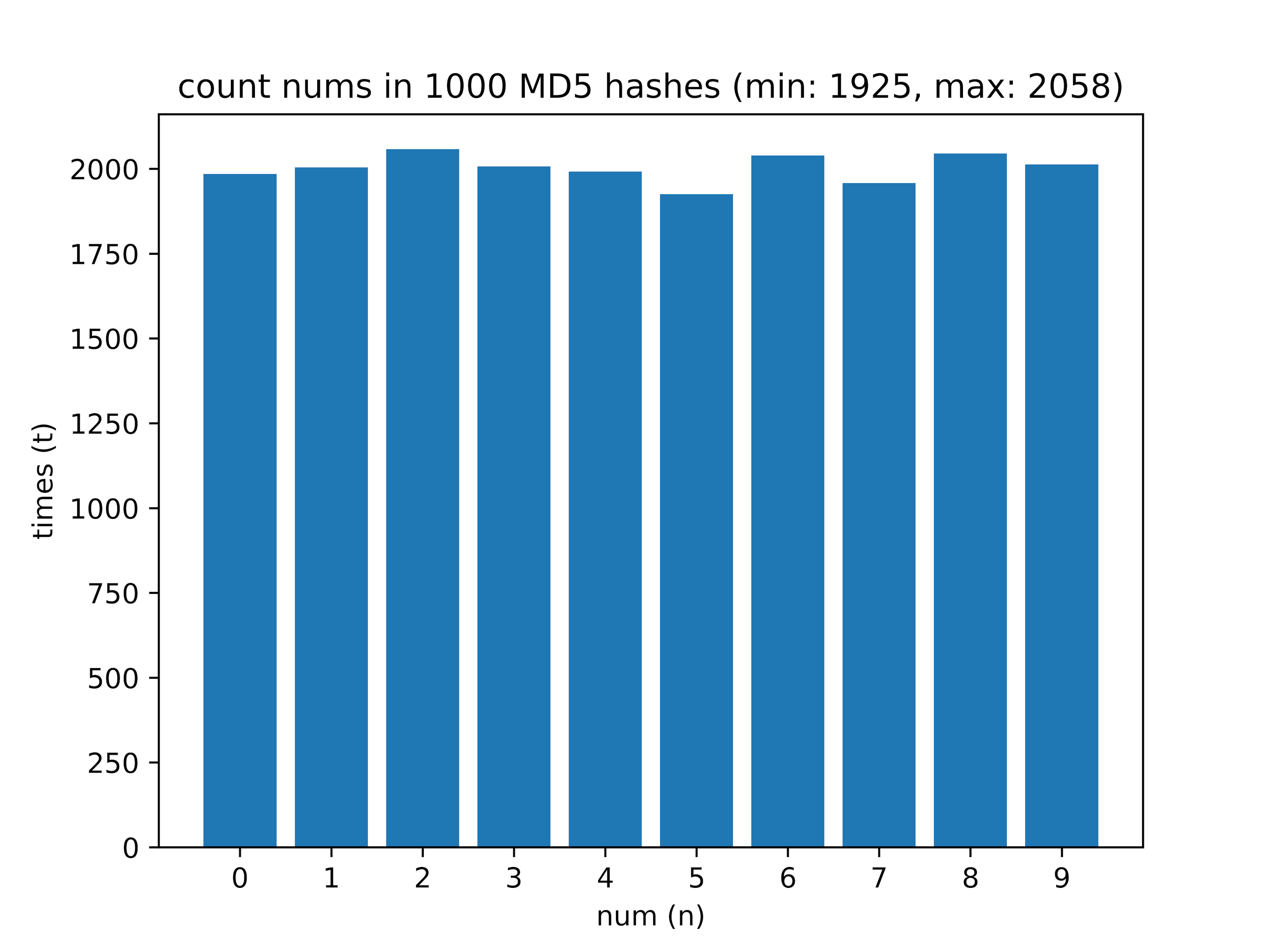
Here the difference between the most frequently encountered digit and the most rarely found (delta value) is interesting.

Further, in order to trace the change in the delta value, he made samples of 10,000, 100,000, 1,000,000, 10,000,000 hashes.

The following is a list with the values of the minimum and maximum numbers and the delta value on samples with different numbers of MD5 hashes:
What we have: with an increase in the number of hashes in the array, the delta value decreases and any digit with almost the same probability will fall into the array. Thus, the larger the sample, the smaller the difference between frequently encountered and rarely seen numbers. Accordingly, the probability of obtaining a particular digit in a hash tends to uniformity.
This information formed the basis of the algorithm that we implemented on the bepeam.com competition platform
First, I generated a random string of characters (length from 0 to 1000).
def random_string(from_int, to_int):
return str(''.join(random.SystemRandom().choice(string.ascii_letters + string.digits + string.punctuation) for _ in range(random.randint(from_int, to_int))))Next, I took the MD5 hash from the string.
def md5_from_string(string):
return hashlib.md5(string.encode('utf-8')).hexdigest()After - I calculated how many digits from 0 to 9 are in the hash. On a sample of 1000 hashes, I received the following data:

Here the difference between the most frequently encountered digit and the most rarely found (delta value) is interesting.

Further, in order to trace the change in the delta value, he made samples of 10,000, 100,000, 1,000,000, 10,000,000 hashes.

The following is a list with the values of the minimum and maximum numbers and the delta value on samples with different numbers of MD5 hashes:
- 100 - min: 179, max: 230, delta: 22.17%
- 1000 - min: 1925, max: 2058, delta: 6.46%
- 10000 - min: 19769, max: 20251, delta: 2.38%
- 100000 - min: 199297, max: 200846, delta: 0.77%
- 1,000,000 - min: 1997650, max: 2001690, delta: 0.20%
- 10000000 - min: 19991830, max: 20004818, delta: 0.06%
What we have: with an increase in the number of hashes in the array, the delta value decreases and any digit with almost the same probability will fall into the array. Thus, the larger the sample, the smaller the difference between frequently encountered and rarely seen numbers. Accordingly, the probability of obtaining a particular digit in a hash tends to uniformity.
This information formed the basis of the algorithm that we implemented on the bepeam.com competition platform
