A brief history of Lambda, or why Ethan is lying
In the next opus Ethan Siegel rezanula phrase

wat?
What kind of surprise can we talk about? There, after all, an absolutely gorgeous story 80 years long with bright discoveries and closures. A story about how real science is actually done. The story is more about physicists than about physics.
Albert Einstein presented the first version of the General Theory of Relativity (GR) to the public on November 25, 1915. In the original, Einstein's equations of general relativity looked like this:

or, in a modern notation, like this:
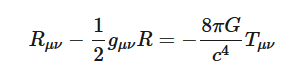
For a reader who is not familiar with tensors, equation (1) in Einstein’s original entry is more understandable. It says that the energy-momentum of matter G is equal to the curvature of the space R plus the Ricci tensor S. (This same Ricci tensor is also the curvature, only in a more different form).
Now, when solving the equation of general relativity, energy-momentum is usually considered known, and just the curvature is sought. Therefore, in the modern record, the sides of the equation are reversed. At the same time, we changed the letters: G → T, S → R μν .
One of the first serious mathematicians who began to check Einstein's calculations was Eli Joseph Cartan (not to be confused with his son Henri, also a famous mathematician).
Cartan Papa found a number of technical errors with Einstein, in particular, one that is known to the modern generation of the exam as code-named "lose a constant during integration." Today, this lost constant is denoted by the Greek capital letter lambda, Λ.
But physics is not mathematics for you. Here you can’t take the formula and cram additional terms into it for no reason. It is necessary to have very good reasons, both theoretical and experimental.
Although below you will see how little Einstein knew about the Universe in those years, but then, in 1916, he had such reasons. Albert Germanovich knew for sure that the stars did not fall on each other and were completely not going to do this in the foreseeable future. However, in OTO-1915 there was only an attraction that needed to be balanced with something.
The lambda introduced into the equations was just responsible for repulsion. Therefore, in 1917, Einstein published the “augmented and improved” version of GR with the cosmological constant Λ. In modern notation, the equation looks like this:

Take the OTO-1917 equation and take out the metric tensor . Then inside the brackets we will have the expression (R / 2 - Λ). Here R without indices is the usual “school” scalar curvature. If on fingers - this is the reciprocal of the radius of the circle / sphere. A flat space corresponds to R = 0.
. Then inside the brackets we will have the expression (R / 2 - Λ). Here R without indices is the usual “school” scalar curvature. If on fingers - this is the reciprocal of the radius of the circle / sphere. A flat space corresponds to R = 0.
In this interpretation, a non-zero value of Λ means that our Universe is curved on its own, including in the absence of any gravity. Well, here we have such a world. However, most physicists do not believe this, and believe that the observed curvature must have some internal reason. Some hitherto unknown garbage that can be opened.
Meanwhile in Russia, despite the wars and revolutions, the ensign (and part-time professor) Alexander Aleksandrovich Fridman fought over the theory of general relativity. He considered all options for lambdas and found out the following:
For Λ <0, there are only attractive forces, both gravitational and caused by the curvature of theconvex concave space. Sooner or later, the stars and galaxies in such a world still fall on each other. And the end will be unexpectedly fast and very hot.
At Λ> 0, geometry drives at large distances, and stars and galaxies scatter “off the hill” (Einstein-1917 variant). With a sufficiently large lambda in the sky, there may not even be a single star left except the Sun, with a moderate value - only our galaxy will merge with its nearest neighbors.
But the most interesting thing happens when Λ = 0. Here everything depends on the initial conditions - i.e. coordinates and speeds of specific galaxies. Three options are possible: large compression, large expansion, and the stationary version, when the galaxies fly apart, but with relatively low speeds and without acceleration.
Today, the situations described above are called Friedmann's cosmological decisions.
Friedman's articles of 1922 and 1924 abolished the need for a lambda member, which is why Einstein initially took hostility.
For his work, Friedman could well claim the Nobel Prize.
From the decisions of Friedman it followed that the Universe could have a beginning. This idea was picked up by many physicists, and headed by what was later called the "Big Bang Theory", Russian-American Georgy Gamov, who assumed Λ = 0.
And yes, Ethan's article about something like this graph (specifically for this, the data for 2010 are taken into account):
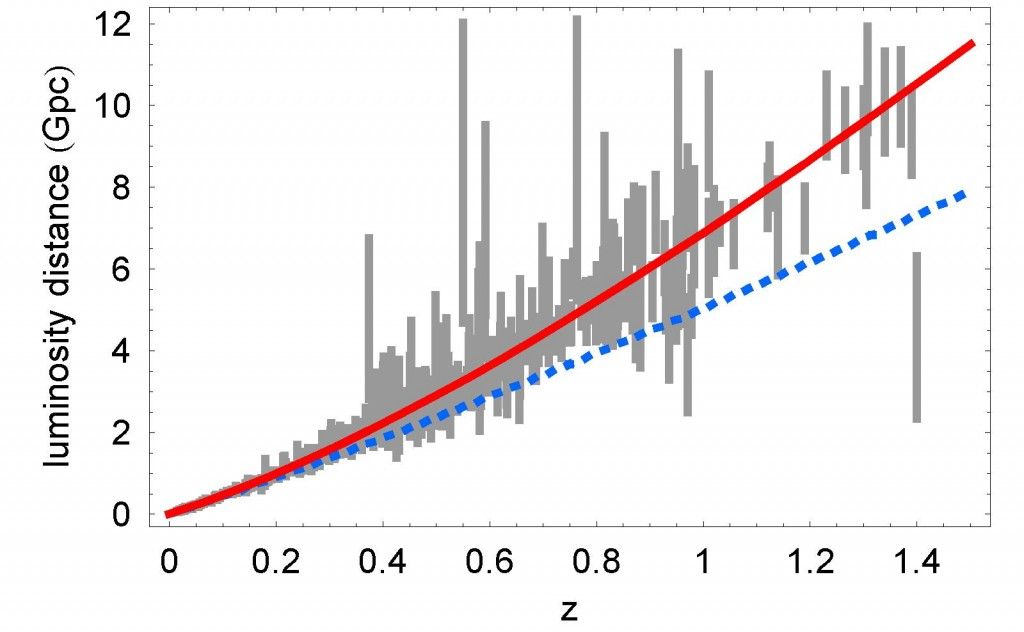
Here z is horizontally plotted - this is the redshift, the vertical brightness of supernovae of a special type Ia, which always emit the same amount of energy. In general, these are two ways of measuring the same distance, but, so to speak, at different points in time.
Gray sticks are the observed events with their measurement error. The blue dotted line represents the prediction at Λ = 0, the red line represents the approximation of the actually observed values. Deviation of the red line from the line means that the Universe is expanding rapidly. But Einstein never found out.
Let's move on to the experimental part.
The Dutch astronomer Jacobus Cornelius Kaptein discovered the Kaptein star in 1897, after which he proceeded to the opus magnum of his whole life. Combining a huge number of observations from different observatories, he tried to create the first map of the universe. According to his map, the universe appeared to be in the form of a rotating (sic!) Disk of a roof-covering disk at that time of the size of 40,000 light-years, and the Sun is not at all in the center, but at its very backyard. This work was completed and published only in 1922.
To understand the level of knowledge at that time: what Kapteyn considered the incredibly vast Universe is today considered to be completely ordinary, unremarkable among billions of the same ... Milky Way galaxies. However, Kaptein's merit is that he discovered its rotation and approximately calculated its center.
Speaking of astronomers, Edwin Hubble did the most for lambda history. He felt that something was wrong with the nebulae, and in 1922 suggested that some of them were not clouds of gas, but very distant objects. Testing his theory, in 1924 he was the first in the world to discern individual stars in the Andromeda nebula (yes, he was lucky all his life with very good telescopes. And after death he continued to carry). It was Hubble who proposed the term “galaxy” - in fact, this is the “Milky Way” in Greek.
Hubble presented the article with his discoveries, which implied that the Universe is much larger than our Milky Way, to the American Astronomical Society on January 1, 1925. For this, he was booed byhis hungry colleagues who were hardly accustomed to Kaptain's distances.
Hubble did not let up, and he also attached a spectrometer to the telescope. Analyzing the redshift of the galaxies, he found out that the galaxies are scattering, and the Universe, accordingly, is expanding. At the same time, he discovered the law of the name of himself with a constant name of himself (however, the law was predicted by Lemeter), and described all this in articles by the end of the 20s. According to his observations, the Friedman model for Λ = 0 turned out to be true.
This has now eliminated the experimental grounds for its existence from under the lambda.
Einstein, looking at this, promptly deleted the cosmological constant from the equations of general relativity, and at the end of his life he considered the lambda story “his biggest mistake”.
So, besides all his discoveries, Hubble also involuntarily “closed” the lambda. For as many as 70 years.
It should also be mentioned here that the initial estimates of Hubble were very inaccurate and showed the age of the Universe on the order of 2 billion years. Later, this will contradict the data of geophysicists, who, using radioisotope analysis, will estimate the Earth’s age as several billion years, and for decades it will be a great headache for cosmologists.
Since the beginning of the 30s, the issue with lambda was considered resolved, and of the mainstream physicists, nobody really dealt with it. One of the rare exceptions that dared to trample against Einstein himself was Briton Fred Hoyle.
Hoyle was a very authoritative scientist in the field of cosmology, and, unlike many colleagues, he was so-called “applied”, i.e. relatively easily verifiable cosmology. It was he who explained how stars and galaxies are formed from homogeneous rarefied gas clouds by gravitational compression. It was also Hoyle who came up with the name “Big Bang”, and he used this name in an abusive sense.
Hoyle and his co-authors - Bondi and Gold - did not like the “big pop” (a more correct translation of the phrase big bang), in which the Universe has a beginning. They believed that just as all points in space are equal, all points in time should be equal. Such a universe has no beginning or end, and at the same time it is constantly, although very slowly expanding.
However, a new substance is constantly born from quantum fluctuations, and so that the average density of matter remains the same. Calculations show that in one cubic kilometer of space, only one proton should be born every 300,000 years (as well as one electron or something like that to save an electric charge). A great number to rule out any possibility of any experimental verification!
The theory of the stationary Universe was seriously considered as an alternative to the Big Bang theory in the 50s and early 60s. But the experimental discovery in 1964 of the predicted TBB relict radiation put an end to it.
Hoyle, however, did not let up and improved his theory until his retirement. The latest edition, developed in conjunction with his friend Jeffrey Burbidge in 1993, the so-called “quasi-stationary Universe,” suggests local mini-explosions and explains almost all of the observed facts, but is not popular. And yes, it is suspiciously similar to the generally accepted theory of inflation today (but it differs by plus or minus signs in some places).
For the B²FH article they gave the Nobel Prize. But only Fowler, who ordered a ten-day experiment. Neither the Burbidjam spouses, who carried out long astronomical observations and actually wrote the article, nor the author of the idea, Hoyle, were given the Nobel for insisting on a cosmological heresy.
The most interesting thing is that Hoyle lived up to the experimental confirmation of the accelerated recession of galaxies in 1998. But even this did not become an occasion for the Nobel Committee to correct an obvious error.
Let us return to the equation of general relativity.
On the left (in the modern record) is the curvature of space, in other words, gravity by GR. On the right is the energy-momentum tensor. Under this tensor there is a terribly complex matan, but the essence is as follows: all-all-all matter of the Universe is taken into account in all forms and states. And ordinary matter, and all sorts of tricky particles, and all kinds of radiation (except gravity, which is on the left).
Now mentally move the lambda to the right. In such a record, this will not be additional curvature, but some unaccounted-for energy (I note negative, since we consider lambda positive). And here are two possibilities.
The first hypothesis is that lambda is the energy of the vacuum itself. Sounds wild, but actually quite consistent with quantum mechanics. Take a piece of space and remove from it everything that, at least in principle, can be removed. We remove all matter, all particles and all waves, regardless of their nature. Only physical fields in an undisturbed state will remain. Full calm.
So, some fields (for example, Higgs) have a nonzero value in the void. And theoretically, they have some energy. In addition, by virtue of the uncertainty principle, any fields have quantum fluctuations - and they also have some energy.
There is, however, a small technical problem. If everything is carefully calculated, the calculated result differs from that observed by 120 - no, more than once, by 120 orders of magnitude. 100 billion google times! This is rightly considered the "worst prediction in the history of theoretical physics."
The second possibility: physicists still forgot to calculate something when they calculated the energy-momentum tensor. This “something” should be very strange (give negative pressure), we don’t know anything like it yet, so here the situation is more likely “didn’t know - did not know, and forgot”. Now this "something" is called "dark energy", and this energy should be about twice as much as the energy of ordinary and dark matter combined. ← Modern physics is here.
Bells about the nonzero value of lambda began to appear at the turn of the 90s - from accurate measurements of CMB radiation, etc., and by 1997 had turned into an alarm. It is not surprising that immediately two groups of physicists armed themselves with modern tools and rushed to recheck Hubble’s grandfather. Therefore, when Ethan writes about “completely unexpectedly,” he, to put it mildly, is lying.
And while we have nothing better than “dark energy” to explain lambda, this story will continue.
Thanks for attention!

After observing distant supernovae and measuring how the universe expanded over billions of years, astronomers have discovered something surprising, mysterious and unexpected .And no, everything is in order with the translation, the original is even yellower:
By observing distant supernovae and measuring how the Universe had expanded over billions of years, astronomers discovered something remarkable, puzzling and completely unexpected
wat?
What kind of surprise can we talk about? There, after all, an absolutely gorgeous story 80 years long with bright discoveries and closures. A story about how real science is actually done. The story is more about physicists than about physics.
What is the whole fuss about?
Albert Einstein presented the first version of the General Theory of Relativity (GR) to the public on November 25, 1915. In the original, Einstein's equations of general relativity looked like this:

or, in a modern notation, like this:
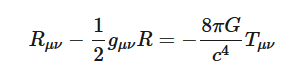
For a reader who is not familiar with tensors, equation (1) in Einstein’s original entry is more understandable. It says that the energy-momentum of matter G is equal to the curvature of the space R plus the Ricci tensor S. (This same Ricci tensor is also the curvature, only in a more different form).
Now, when solving the equation of general relativity, energy-momentum is usually considered known, and just the curvature is sought. Therefore, in the modern record, the sides of the equation are reversed. At the same time, we changed the letters: G → T, S → R μν .
Where did lambda come from
One of the first serious mathematicians who began to check Einstein's calculations was Eli Joseph Cartan (not to be confused with his son Henri, also a famous mathematician).
Cartan Papa found a number of technical errors with Einstein, in particular, one that is known to the modern generation of the exam as code-named "lose a constant during integration." Today, this lost constant is denoted by the Greek capital letter lambda, Λ.
But physics is not mathematics for you. Here you can’t take the formula and cram additional terms into it for no reason. It is necessary to have very good reasons, both theoretical and experimental.
Although below you will see how little Einstein knew about the Universe in those years, but then, in 1916, he had such reasons. Albert Germanovich knew for sure that the stars did not fall on each other and were completely not going to do this in the foreseeable future. However, in OTO-1915 there was only an attraction that needed to be balanced with something.
The lambda introduced into the equations was just responsible for repulsion. Therefore, in 1917, Einstein published the “augmented and improved” version of GR with the cosmological constant Λ. In modern notation, the equation looks like this:
The first physical interpretation of the meaning of lambda
Take the OTO-1917 equation and take out the metric tensor
In this interpretation, a non-zero value of Λ means that our Universe is curved on its own, including in the absence of any gravity. Well, here we have such a world. However, most physicists do not believe this, and believe that the observed curvature must have some internal reason. Some hitherto unknown garbage that can be opened.
What's wrong with curvature measurements
To date, the measured curvature of the space of the Universe is still zero, but with very lousy accuracy, of the order of 0.4%. And not very visible ways to improve this accuracy.
There are two conceptual issues with curvature measurements.
The first is that we cannot measure completely empty space, because we simply don’t see anything there. And if there is something that we still see, then the space is no longer empty and, therefore, is already additionally curved by gravity.
The second problem is more complicated and has a personal name “reference frame problem”. The point is this.
Suppose we have somehow measured the coordinates of objects, plus a bunch of photos of these objects from different angles (taken from different points). Then we can calculate the curvature of space. For example, the gravity of the Sun deflects the passing light of distant stars. During solar eclipses, this deviation can be measured experimentally and compared with GR predictions.
Now, on the contrary: let's say we know the curvature of space, and we have a bunch of photos. Then, if the curvature is good enough, without black holes, etc. - we can calculate the coordinates of the objects in the photo. This is how our eyes work, or rather brains, when they calculate the distance to objects from two photos from different points.
But for distant galaxies, everything is bad. We do not know their exact coordinates. And the curvature of space on a large scale, we also do not know. And we don’t even have a pack of photos: on such a scale, we can assume that they are all made from almost one point. Therefore, outside the Milky Way, we can not be sure of either the coordinates or the curvature.
And due to the universality of gravity, this applies not only to the "photographs" themselves, but to absolutely any measurements of distant objects.
Therefore, we can measure the curvature of the observed Universe as a whole only from very circumstantial considerations.
There are two conceptual issues with curvature measurements.
The first is that we cannot measure completely empty space, because we simply don’t see anything there. And if there is something that we still see, then the space is no longer empty and, therefore, is already additionally curved by gravity.
The second problem is more complicated and has a personal name “reference frame problem”. The point is this.
Suppose we have somehow measured the coordinates of objects, plus a bunch of photos of these objects from different angles (taken from different points). Then we can calculate the curvature of space. For example, the gravity of the Sun deflects the passing light of distant stars. During solar eclipses, this deviation can be measured experimentally and compared with GR predictions.
Now, on the contrary: let's say we know the curvature of space, and we have a bunch of photos. Then, if the curvature is good enough, without black holes, etc. - we can calculate the coordinates of the objects in the photo. This is how our eyes work, or rather brains, when they calculate the distance to objects from two photos from different points.
But for distant galaxies, everything is bad. We do not know their exact coordinates. And the curvature of space on a large scale, we also do not know. And we don’t even have a pack of photos: on such a scale, we can assume that they are all made from almost one point. Therefore, outside the Milky Way, we can not be sure of either the coordinates or the curvature.
And due to the universality of gravity, this applies not only to the "photographs" themselves, but to absolutely any measurements of distant objects.
Therefore, we can measure the curvature of the observed Universe as a whole only from very circumstantial considerations.
Friedman Universe
Meanwhile in Russia, despite the wars and revolutions, the ensign (and part-time professor) Alexander Aleksandrovich Fridman fought over the theory of general relativity. He considered all options for lambdas and found out the following:
For Λ <0, there are only attractive forces, both gravitational and caused by the curvature of the
At Λ> 0, geometry drives at large distances, and stars and galaxies scatter “off the hill” (Einstein-1917 variant). With a sufficiently large lambda in the sky, there may not even be a single star left except the Sun, with a moderate value - only our galaxy will merge with its nearest neighbors.
But the most interesting thing happens when Λ = 0. Here everything depends on the initial conditions - i.e. coordinates and speeds of specific galaxies. Three options are possible: large compression, large expansion, and the stationary version, when the galaxies fly apart, but with relatively low speeds and without acceleration.
Today, the situations described above are called Friedmann's cosmological decisions.
Friedman's articles of 1922 and 1924 abolished the need for a lambda member, which is why Einstein initially took hostility.
For his work, Friedman could well claim the Nobel Prize.
But
In the summer of 1925 he got married, went on a honeymoon to the Crimea, ate an unwashed pear there, contracted typhus and died in September.
From the decisions of Friedman it followed that the Universe could have a beginning. This idea was picked up by many physicists, and headed by what was later called the "Big Bang Theory", Russian-American Georgy Gamov, who assumed Λ = 0.
And yes, Ethan's article about something like this graph (specifically for this, the data for 2010 are taken into account):

Here z is horizontally plotted - this is the redshift, the vertical brightness of supernovae of a special type Ia, which always emit the same amount of energy. In general, these are two ways of measuring the same distance, but, so to speak, at different points in time.
Gray sticks are the observed events with their measurement error. The blue dotted line represents the prediction at Λ = 0, the red line represents the approximation of the actually observed values. Deviation of the red line from the line means that the Universe is expanding rapidly. But Einstein never found out.
Kaptein Universe
Let's move on to the experimental part.
The Dutch astronomer Jacobus Cornelius Kaptein discovered the Kaptein star in 1897, after which he proceeded to the opus magnum of his whole life. Combining a huge number of observations from different observatories, he tried to create the first map of the universe. According to his map, the universe appeared to be in the form of a rotating (sic!) Disk of a roof-covering disk at that time of the size of 40,000 light-years, and the Sun is not at all in the center, but at its very backyard. This work was completed and published only in 1922.
To understand the level of knowledge at that time: what Kapteyn considered the incredibly vast Universe is today considered to be completely ordinary, unremarkable among billions of the same ... Milky Way galaxies. However, Kaptein's merit is that he discovered its rotation and approximately calculated its center.
Hubble Observations (Astronomer, Not Telescope)
Speaking of astronomers, Edwin Hubble did the most for lambda history. He felt that something was wrong with the nebulae, and in 1922 suggested that some of them were not clouds of gas, but very distant objects. Testing his theory, in 1924 he was the first in the world to discern individual stars in the Andromeda nebula (yes, he was lucky all his life with very good telescopes. And after death he continued to carry). It was Hubble who proposed the term “galaxy” - in fact, this is the “Milky Way” in Greek.
Hubble presented the article with his discoveries, which implied that the Universe is much larger than our Milky Way, to the American Astronomical Society on January 1, 1925. For this, he was booed by
Hubble did not let up, and he also attached a spectrometer to the telescope. Analyzing the redshift of the galaxies, he found out that the galaxies are scattering, and the Universe, accordingly, is expanding. At the same time, he discovered the law of the name of himself with a constant name of himself (however, the law was predicted by Lemeter), and described all this in articles by the end of the 20s. According to his observations, the Friedman model for Λ = 0 turned out to be true.
This has now eliminated the experimental grounds for its existence from under the lambda.
Einstein, looking at this, promptly deleted the cosmological constant from the equations of general relativity, and at the end of his life he considered the lambda story “his biggest mistake”.
So, besides all his discoveries, Hubble also involuntarily “closed” the lambda. For as many as 70 years.
It should also be mentioned here that the initial estimates of Hubble were very inaccurate and showed the age of the Universe on the order of 2 billion years. Later, this will contradict the data of geophysicists, who, using radioisotope analysis, will estimate the Earth’s age as several billion years, and for decades it will be a great headache for cosmologists.
Hoyle Stationary Universe
Since the beginning of the 30s, the issue with lambda was considered resolved, and of the mainstream physicists, nobody really dealt with it. One of the rare exceptions that dared to trample against Einstein himself was Briton Fred Hoyle.
Offtopic about Hoyle, carbon and three alpha
It will be about helium. This element is phenomenally inert and does not want to react with anything. And not only chemically, but also physically, if we are talking about helium-4. Its core - an alpha particle - has a peak binding energy per nucleon in its region. see pic from some abstract:
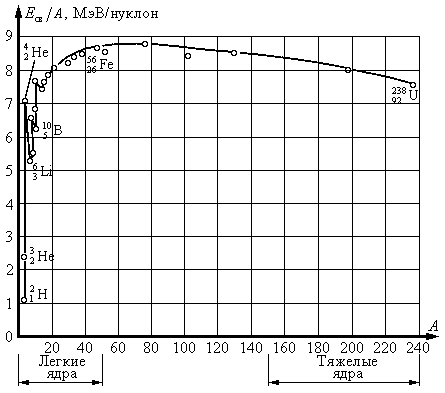
This means that an alpha particle cannot attach additional protons or another alpha particle except by chance: it is simply energetically disadvantageous. And in the nuclei of stars there is nothing but protons and alpha particles.
A reasonable question arose: where did the chemical elements heavier than helium come from?
The nearest nucleus that helium-4 can turn into is carbon-12. But for this you need to combine the three alpha particles.
The problem is that the probability of a collision of three alpha particles at the same time is too small. A two-step process (at first two particles collide, then very quickly, until they scatter back into two alpha particles, another one crashes into them), in principle, it is possible, but Edwin Salpeter's calculations showed that such a process is too sluggish to produce significant amounts of carbon.
And in the spring of 1953, Briton Fred Hoyle arrived in Caltech, then still without the prefix “sir”, and immediately went to the local meager William Fowler.
There he asked from the threshold: can carbon-12 have an energy level of 7.69 MeV? At first, Fowler thought that another madman had pinned him, but he decided to ask, “Actually, no, but what do you really need?” To which Hoyle replied: Well, I exist, which means that the carbon nucleus should have such an energy level. Great argument!
However, according to Hoyle’s calculations, it turned out that if there is such a level in the three-alpha process, resonance occurs, and the stars - red giants produce quite a lot of carbon for our existence.
Surprisingly, the Americans decided to conduct a small experiment on their accelerator. And yes - they triumphantly found the necessary energy level at 7.65 MeV, which for some reason nuclear physicists around the world overlooked in all previous experiments.
Today, such an excited state of carbon-12, when three alpha particles actually line up, is called Hoyle. The related article by Hoyle, Fowler, and astronomer spouses Jeffrey and Marguerite Burbidgey is the cornerstone of modern stellar nucleosynthesis theories and is so often cited that it simply denotes B²FH, without reference or decoding.
And - yes, today it is almost the only known successful prediction based on the anthropic principle.

This means that an alpha particle cannot attach additional protons or another alpha particle except by chance: it is simply energetically disadvantageous. And in the nuclei of stars there is nothing but protons and alpha particles.
A reasonable question arose: where did the chemical elements heavier than helium come from?
The nearest nucleus that helium-4 can turn into is carbon-12. But for this you need to combine the three alpha particles.
The problem is that the probability of a collision of three alpha particles at the same time is too small. A two-step process (at first two particles collide, then very quickly, until they scatter back into two alpha particles, another one crashes into them), in principle, it is possible, but Edwin Salpeter's calculations showed that such a process is too sluggish to produce significant amounts of carbon.
And in the spring of 1953, Briton Fred Hoyle arrived in Caltech, then still without the prefix “sir”, and immediately went to the local meager William Fowler.
There he asked from the threshold: can carbon-12 have an energy level of 7.69 MeV? At first, Fowler thought that another madman had pinned him, but he decided to ask, “Actually, no, but what do you really need?” To which Hoyle replied: Well, I exist, which means that the carbon nucleus should have such an energy level. Great argument!
However, according to Hoyle’s calculations, it turned out that if there is such a level in the three-alpha process, resonance occurs, and the stars - red giants produce quite a lot of carbon for our existence.
Surprisingly, the Americans decided to conduct a small experiment on their accelerator. And yes - they triumphantly found the necessary energy level at 7.65 MeV, which for some reason nuclear physicists around the world overlooked in all previous experiments.
Today, such an excited state of carbon-12, when three alpha particles actually line up, is called Hoyle. The related article by Hoyle, Fowler, and astronomer spouses Jeffrey and Marguerite Burbidgey is the cornerstone of modern stellar nucleosynthesis theories and is so often cited that it simply denotes B²FH, without reference or decoding.
And - yes, today it is almost the only known successful prediction based on the anthropic principle.
Hoyle was a very authoritative scientist in the field of cosmology, and, unlike many colleagues, he was so-called “applied”, i.e. relatively easily verifiable cosmology. It was he who explained how stars and galaxies are formed from homogeneous rarefied gas clouds by gravitational compression. It was also Hoyle who came up with the name “Big Bang”, and he used this name in an abusive sense.
Hoyle and his co-authors - Bondi and Gold - did not like the “big pop” (a more correct translation of the phrase big bang), in which the Universe has a beginning. They believed that just as all points in space are equal, all points in time should be equal. Such a universe has no beginning or end, and at the same time it is constantly, although very slowly expanding.
However, a new substance is constantly born from quantum fluctuations, and so that the average density of matter remains the same. Calculations show that in one cubic kilometer of space, only one proton should be born every 300,000 years (as well as one electron or something like that to save an electric charge). A great number to rule out any possibility of any experimental verification!
The theory of the stationary Universe was seriously considered as an alternative to the Big Bang theory in the 50s and early 60s. But the experimental discovery in 1964 of the predicted TBB relict radiation put an end to it.
Hoyle, however, did not let up and improved his theory until his retirement. The latest edition, developed in conjunction with his friend Jeffrey Burbidge in 1993, the so-called “quasi-stationary Universe,” suggests local mini-explosions and explains almost all of the observed facts, but is not popular. And yes, it is suspiciously similar to the generally accepted theory of inflation today (but it differs by plus or minus signs in some places).
For the B²FH article they gave the Nobel Prize. But only Fowler, who ordered a ten-day experiment. Neither the Burbidjam spouses, who carried out long astronomical observations and actually wrote the article, nor the author of the idea, Hoyle, were given the Nobel for insisting on a cosmological heresy.
The most interesting thing is that Hoyle lived up to the experimental confirmation of the accelerated recession of galaxies in 1998. But even this did not become an occasion for the Nobel Committee to correct an obvious error.
Quantum lambda
Let us return to the equation of general relativity.
On the left (in the modern record) is the curvature of space, in other words, gravity by GR. On the right is the energy-momentum tensor. Under this tensor there is a terribly complex matan, but the essence is as follows: all-all-all matter of the Universe is taken into account in all forms and states. And ordinary matter, and all sorts of tricky particles, and all kinds of radiation (except gravity, which is on the left).
Now mentally move the lambda to the right. In such a record, this will not be additional curvature, but some unaccounted-for energy (I note negative, since we consider lambda positive). And here are two possibilities.
The first hypothesis is that lambda is the energy of the vacuum itself. Sounds wild, but actually quite consistent with quantum mechanics. Take a piece of space and remove from it everything that, at least in principle, can be removed. We remove all matter, all particles and all waves, regardless of their nature. Only physical fields in an undisturbed state will remain. Full calm.
So, some fields (for example, Higgs) have a nonzero value in the void. And theoretically, they have some energy. In addition, by virtue of the uncertainty principle, any fields have quantum fluctuations - and they also have some energy.
There is, however, a small technical problem. If everything is carefully calculated, the calculated result differs from that observed by 120 - no, more than once, by 120 orders of magnitude. 100 billion google times! This is rightly considered the "worst prediction in the history of theoretical physics."
The second possibility: physicists still forgot to calculate something when they calculated the energy-momentum tensor. This “something” should be very strange (give negative pressure), we don’t know anything like it yet, so here the situation is more likely “didn’t know - did not know, and forgot”. Now this "something" is called "dark energy", and this energy should be about twice as much as the energy of ordinary and dark matter combined. ← Modern physics is here.
Instead of a conclusion
Bells about the nonzero value of lambda began to appear at the turn of the 90s - from accurate measurements of CMB radiation, etc., and by 1997 had turned into an alarm. It is not surprising that immediately two groups of physicists armed themselves with modern tools and rushed to recheck Hubble’s grandfather. Therefore, when Ethan writes about “completely unexpectedly,” he, to put it mildly, is lying.
And while we have nothing better than “dark energy” to explain lambda, this story will continue.
Thanks for attention!
