Blockchain on Go. Part 2: Proof-of-Work
- From the sandbox
- Tutorial
Hello, Habr! I present to you the translation of the article " Building Blockchain in Go. Part 2: Proof-of-Work ".
Content
In the previous article, we built a very simple data structure, which is the basis for the blockchain database. We also added blocks to it with a chain connection between them: each block is associated with the previous one. Alas, our implementation of the blockchain has one significant drawback: adding blocks to the chain is too simple and cheap.
One of the cornerstones of Bitcoin and blockchain is that adding new blocks should be quite complicated work. And now we are going to fix this shortcoming.
The key idea of the blockchain is that some complex work needs to be done to add a new block. It is this complex work that makes the blockchain reliable and holistic. In addition, a reward is paid for this complex work (this is how people get coins for mining).
This mechanism is similar to real life: you have to work hard to get rewards and secure your life. In the blockchain, some participants (miners) of the network work on maintaining the network, adding new blocks to the blockchain and receive rewards for their work. As a result of their work, the block is embedded in the blockchain in a reliable way, which ensures the stability of the entire blockchain database. It is worth noting that the one who completed the work must also prove its implementation.
This whole “do the hard work and prove it” -mechanism is called Proof-of-Work (proof of work). It is complicated because it requires large computing power: even high-performance computers cannot quickly execute it. Moreover, the complexity of this work is gradually increasing in order to create on average about 6 blocks per hour. In Bitcoin, the goal of this work is to find a block hash that satisfies certain requirements. This hash serves as a proof. Thus, the search for evidence is the actual work.
One thing to note: Proof-of-Work algorithms must meet the following requirement: the work must be complex, but the proof must be simple. Verification of the evidence is usually transferred to someone outside, so they should not take this verification a lot of time.
This part is about hashing. Those who are familiar with this concept may skip this part.
Hashing is the process of obtaining a hash for some data. A hash is a unique representation for the data for which it was calculated. A hash function is a function that receives a hash of a specific size for data of arbitrary size. Some key features of hashing are:
Hash functions are widely used to verify data integrity. Many software vendors publish their checksums with the software. After downloading the file, you need to feed the hash functions, and then compare the resulting hash with what the software developer published.
On the blockchain, a hash is used to guarantee the integrity of the block. The input for the hashing algorithm contains the hash of the previous block, which makes it impossible (or at least very complicated) to change the block in the chain: you will have to recalculate the hash of the block itself, as well as the hashes of all the blocks following it.
Bitcoin uses Hashcash , a Proof-of-Work algorithm that was developed to protect against email spam. The algorithm can be divided into the following steps:
Thus, this is a brute force algorithm: change the counter, calculate the hash, check it, increase the counter, calculate the hash again, and so on. That is why the algorithm is computationally expensive.
Now consider the requirements that the hash must satisfy. In the original Hashcash implementation, the requirement sounds like "the first 20 bits of the hash must be zero." In Bitcoin, the requirement is adjusted from time to time, because according to the plan, the block should be generated every 10 minutes, despite the fact that the computing power grows with time and more and more miners join the network.
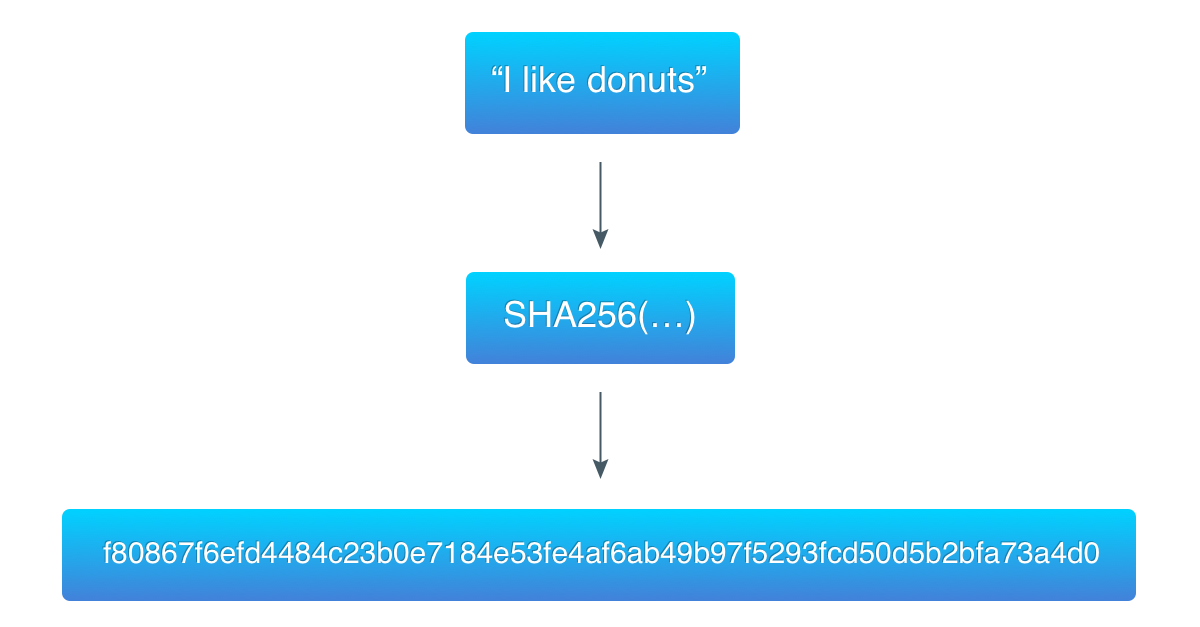
To demonstrate the algorithm, take the previous example (“I like donuts”) and find a hash that starts with three zero bytes.

So, with the theory over, let's get down to code. First, let's determine the complexity of mining:
In Bitcoin, “target bits” is a block header field that stores the complexity on which the block was mined. We will not build a correcting algorithm, so we define complexity as a global constant.
24 is an arbitrary number, our goal is to have complexity, which takes up less than 256 bits in memory. And we want the difference to be significant enough, but not too big, because the larger the difference, the more difficult it is to find the correct hash.
Here we create create
In the function,
And it takes up 29 bytes in memory. And here is a visual comparison with the hashes from previous examples:
The first hash (calculated for “I like donuts”) is larger than the target, so this is not a valid proof of work. The second hash (calculated for "I like donutsca07ca") is less than the target, so this is a good proof.
You can consider the target as the upper boundary of the range: if the number (hash) is less than the boundary, then it is suitable, and vice versa. Lowering the border will reduce the number of suitable numbers, thereby increasing the difficulty of finding the right one.
Now we need hash data. Let's prepare them:
This piece of code is quite simple. We simply combine the fields of the block with the target and "nonce".
So, all the preparations are done. Now we implement the core of the Proof-of-Work algorithm:
First we initialize the variables.
In the loop we do the following:
As easy as explained earlier. Now you can remove the
You may notice that it is
Now run our program and verify that everything works well:
Hurrah! Now you can see that each hash starts with three zero bytes and it takes some time to find the hashes.
There is still something to do: let's make it possible to verify the evidence of work:
This is where we need the saved one
Check that everything is in order:
Output:
Our blockchain is one step closer to the current architecture: adding blocks requires computational work, so mining is possible. But it still lacks some important functions: the blockchain database is not constant, there are no wallets, addresses, transactions, and there is no consensus mechanism. We will consider all these things in the following articles.
Part One
Original article
Source codes for the article Proof of Work Hashcash Blockchain
Hashing Algorithm
Content
- Blockchain on Go. Part 1: Prototype
- Blockchain on Go. Part 2: Proof-of-Work
- Blockchain on Go. Part 3: read-only memory and command line interface
- Blockchain on Go. Part 4: Transactions, Part 1
- Blockchain on Go. Part 5: Addresses
- Blockchain on Go. Part 6: Transactions, Part 2
- Blockchain on Go. Part 7: Network
Introduction
In the previous article, we built a very simple data structure, which is the basis for the blockchain database. We also added blocks to it with a chain connection between them: each block is associated with the previous one. Alas, our implementation of the blockchain has one significant drawback: adding blocks to the chain is too simple and cheap.
One of the cornerstones of Bitcoin and blockchain is that adding new blocks should be quite complicated work. And now we are going to fix this shortcoming.
Proof-of-Work (PoW)
The key idea of the blockchain is that some complex work needs to be done to add a new block. It is this complex work that makes the blockchain reliable and holistic. In addition, a reward is paid for this complex work (this is how people get coins for mining).
This mechanism is similar to real life: you have to work hard to get rewards and secure your life. In the blockchain, some participants (miners) of the network work on maintaining the network, adding new blocks to the blockchain and receive rewards for their work. As a result of their work, the block is embedded in the blockchain in a reliable way, which ensures the stability of the entire blockchain database. It is worth noting that the one who completed the work must also prove its implementation.
This whole “do the hard work and prove it” -mechanism is called Proof-of-Work (proof of work). It is complicated because it requires large computing power: even high-performance computers cannot quickly execute it. Moreover, the complexity of this work is gradually increasing in order to create on average about 6 blocks per hour. In Bitcoin, the goal of this work is to find a block hash that satisfies certain requirements. This hash serves as a proof. Thus, the search for evidence is the actual work.
One thing to note: Proof-of-Work algorithms must meet the following requirement: the work must be complex, but the proof must be simple. Verification of the evidence is usually transferred to someone outside, so they should not take this verification a lot of time.
Hashing
This part is about hashing. Those who are familiar with this concept may skip this part.
Hashing is the process of obtaining a hash for some data. A hash is a unique representation for the data for which it was calculated. A hash function is a function that receives a hash of a specific size for data of arbitrary size. Some key features of hashing are:
- Initial data cannot be recovered from a hash. So hashing is not encryption
- A hash for specific data is always unique and unique.
- Changing one byte in the data results in a completely different hash

Hash functions are widely used to verify data integrity. Many software vendors publish their checksums with the software. After downloading the file, you need to feed the hash functions, and then compare the resulting hash with what the software developer published.
On the blockchain, a hash is used to guarantee the integrity of the block. The input for the hashing algorithm contains the hash of the previous block, which makes it impossible (or at least very complicated) to change the block in the chain: you will have to recalculate the hash of the block itself, as well as the hashes of all the blocks following it.
Hashcash
Bitcoin uses Hashcash , a Proof-of-Work algorithm that was developed to protect against email spam. The algorithm can be divided into the following steps:
- Take publicly known data (for the email, this is the address of the recipient; for bitcoin, this is the title of the block
- Add a counter to them. Counter starts from zero
- Get a hash from a combination
данные+счетчик - Check if the hash meets certain requirements
- If yes, then everything is ready
- If not, increase the counter and repeat steps 3 and 4
Thus, this is a brute force algorithm: change the counter, calculate the hash, check it, increase the counter, calculate the hash again, and so on. That is why the algorithm is computationally expensive.
Now consider the requirements that the hash must satisfy. In the original Hashcash implementation, the requirement sounds like "the first 20 bits of the hash must be zero." In Bitcoin, the requirement is adjusted from time to time, because according to the plan, the block should be generated every 10 minutes, despite the fact that the computing power grows with time and more and more miners join the network.
To demonstrate the algorithm, take the previous example (“I like donuts”) and find a hash that starts with three zero bytes.

ca07ca - This is the hexadecimal representation of the counter, which corresponds to the number 13240266 in decimal.Implementation
So, with the theory over, let's get down to code. First, let's determine the complexity of mining:
const targetBits = 24In Bitcoin, “target bits” is a block header field that stores the complexity on which the block was mined. We will not build a correcting algorithm, so we define complexity as a global constant.
24 is an arbitrary number, our goal is to have complexity, which takes up less than 256 bits in memory. And we want the difference to be significant enough, but not too big, because the larger the difference, the more difficult it is to find the correct hash.
type ProofOfWork struct {
block *Block
target *big.Int
}
func NewProofOfWork(b *Block) *ProofOfWork {
target := big.NewInt(1)
target.Lsh(target, uint(256-targetBits))
pow := &ProofOfWork{b, target}
return pow
}Here we create create
ProofOfWork, which contains a pointer to a pointer to a block and a pointer to a target. “Target” is a different name for the requirements described in the previous part. We use big integer because of the way the hash is compared with the target: we convert the hash to big integer and check if it is smaller than the target. In the function,
NewProofOfWorkwe initialize the big.Intvalue to 1, and then shift it to 256-targetBits bits. 256 Is the length of the SHA-256 hash in bits, and we will use this hash algorithm. Hexadecimal representation target: 0x10000000000000000000000000000000000000000000000000000000000And it takes up 29 bytes in memory. And here is a visual comparison with the hashes from previous examples:
0fac49161af82ed938add1d8725835cc123a1a87b1b196488360e58d4bfb51e3
0000010000000000000000000000000000000000000000000000000000000000
0000008b0f41ec78bab747864db66bcb9fb89920ee75f43fdaaeb5544f7f76ca
The first hash (calculated for “I like donuts”) is larger than the target, so this is not a valid proof of work. The second hash (calculated for "I like donutsca07ca") is less than the target, so this is a good proof.
You can consider the target as the upper boundary of the range: if the number (hash) is less than the boundary, then it is suitable, and vice versa. Lowering the border will reduce the number of suitable numbers, thereby increasing the difficulty of finding the right one.
Now we need hash data. Let's prepare them:
func (pow *ProofOfWork) prepareData(nonce int) []byte {
data := bytes.Join(
[][]byte{
pow.block.PrevBlockHash,
pow.block.Data,
IntToHex(pow.block.Timestamp),
IntToHex(int64(targetBits)),
IntToHex(int64(nonce)),
},
[]byte{},
)
return data
}This piece of code is quite simple. We simply combine the fields of the block with the target and "nonce".
nonce- this is a counter from the description of Hashcash, it is such a cryptographic term. So, all the preparations are done. Now we implement the core of the Proof-of-Work algorithm:
func (pow *ProofOfWork) Run() (int, []byte) {
var hashInt big.Int
var hash [32]byte
nonce := 0
fmt.Printf("Mining the block containing \"%s\"\n", pow.block.Data)
for nonce < maxNonce {
data := pow.prepareData(nonce)
hash = sha256.Sum256(data)
fmt.Printf("\r%x", hash)
hashInt.SetBytes(hash[:])
if hashInt.Cmp(pow.target) == -1 {
break
} else {
nonce++
}
}
fmt.Print("\n\n")
return nonce, hash[:]
}
First we initialize the variables.
hashIntIs an integer representation for hash. nonceIs a counter. Then we start the “infinite” cycle: it is limited by a constant maxNoncewhose value is equal math.MaxInt64. This is done to avoid possible overflow nonce. Although the complexity of our PoW implementation is too small for a counter overflow, just in case it is better to have such a check. In the loop we do the following:
- Prepare data
- Hash their hash256
- Convert hash to big integer
- Compare the resulting integer with the target
As easy as explained earlier. Now you can remove the
SetHashy method Blockand change the function NewBlock:
func NewBlock(data string, prevBlockHash []byte) *Block {
block := &Block{time.Now().Unix(), []byte(data), prevBlockHash, []byte{}, 0}
pow := NewProofOfWork(block)
nonce, hash := pow.Run()
block.Hash = hash[:]
block.Nonce = nonce
return block
}You may notice that it is
noncesaved as a property Block . This is necessary because it nonceis required to verify evidence. The structure Block now looks like this:
type Block struct {
Timestamp int64
Data []byte
PrevBlockHash []byte
Hash []byte
Nonce int
}Now run our program and verify that everything works well:
Mining the block containing "Genesis Block"
00000041662c5fc2883535dc19ba8a33ac993b535da9899e593ff98e1eda56a1
Mining the block containing "Send 1 BTC to Ivan"
00000077a856e697c69833d9effb6bdad54c730a98d674f73c0b30020cc82804
Mining the block containing "Send 2 more BTC to Ivan"
000000b33185e927c9a989cc7d5aaaed739c56dad9fd9361dea558b9bfaf5fbe
Prev. hash:
Data: Genesis Block
Hash: 00000041662c5fc2883535dc19ba8a33ac993b535da9899e593ff98e1eda56a1
Prev. hash: 00000041662c5fc2883535dc19ba8a33ac993b535da9899e593ff98e1eda56a1
Data: Send 1 BTC to Ivan
Hash: 00000077a856e697c69833d9effb6bdad54c730a98d674f73c0b30020cc82804
Prev. hash: 00000077a856e697c69833d9effb6bdad54c730a98d674f73c0b30020cc82804
Data: Send 2 more BTC to Ivan
Hash: 000000b33185e927c9a989cc7d5aaaed739c56dad9fd9361dea558b9bfaf5fbe
Hurrah! Now you can see that each hash starts with three zero bytes and it takes some time to find the hashes.
There is still something to do: let's make it possible to verify the evidence of work:
func (pow *ProofOfWork) Validate() bool {
var hashInt big.Int
data := pow.prepareData(pow.block.Nonce)
hash := sha256.Sum256(data)
hashInt.SetBytes(hash[:])
isValid := hashInt.Cmp(pow.target) == -1
return isValid
}This is where we need the saved one
nonce. Check that everything is in order:
func main() {
...
for _, block := range bc.blocks {
...
pow := NewProofOfWork(block)
fmt.Printf("PoW: %s\n", strconv.FormatBool(pow.Validate()))
fmt.Println()
}
}
Output:
...
Prev. hash:
Data: Genesis Block
Hash: 00000093253acb814afb942e652a84a8f245069a67b5eaa709df8ac612075038
PoW: true
Prev. hash: 00000093253acb814afb942e652a84a8f245069a67b5eaa709df8ac612075038
Data: Send 1 BTC to Ivan
Hash: 0000003eeb3743ee42020e4a15262fd110a72823d804ce8e49643b5fd9d1062b
PoW: true
Prev. hash: 0000003eeb3743ee42020e4a15262fd110a72823d804ce8e49643b5fd9d1062b
Data: Send 2 more BTC to Ivan
Hash: 000000e42afddf57a3daa11b43b2e0923f23e894f96d1f24bfd9b8d2d494c57a
PoW: true
Conclusion
Our blockchain is one step closer to the current architecture: adding blocks requires computational work, so mining is possible. But it still lacks some important functions: the blockchain database is not constant, there are no wallets, addresses, transactions, and there is no consensus mechanism. We will consider all these things in the following articles.
References
Part One
Original article
Source codes for the article Proof of Work Hashcash Blockchain
Hashing Algorithm
