What do coder interviews and the Snake game have in common?

If you were born in the 80s or 90s, you probably heard about Snake . That is, most likely, you spent an insane amount of time on your Nokia 3310, growing a huge snake on a small screen. What else do we remember about Nokia phones?

Their non-discharged battery, right? How did such a “primitive” phone withstand long hours of playing “Snake” without draining the battery?

The short (and incomplete) answer: it's all about the sliding window method .

We would love to write an entire article about Snake , but in this post we will still consider a less spectacular, but nonetheless very important method, and answer questions like:

• Why do we and other programmers consider it a fundamental algorithm?
• Why is it used so often in technical interviews?
• How was it used in Snake and other "real" applications?
• Which of the most popular interview questions can (better) be answered using the sliding window method?

If you are preparing for an interview, reading an article of interest, or want to learn something new, then continue reading. At the same time, you can safely skip the excess and go to the most interesting sections.

NB: If you are only concerned about the “Snake” (and we fully understand you), then you can go to the very end of the post.

---

Let's get started.

Despite the complexity of algorithmic programming, there is a fairly short list of principles necessary for solving problems. One of these principles is the sliding window method .


Figure 1. Sliding window

Window paradigm

The sliding window method arose from the more general principle of cropping.

Framing consists in obtaining the state of the system and limiting the field of view to only its part, called the “window”. This creates a separation between the cropping algorithm and the algorithm applied to those elements that are visible through the window, which simplifies both algorithms.

A special case is a state consisting of a sequence of objects, for example, an array or a string. If you set a window, then we will see a subsequence. Now we can apply any processing to this limited interval, as if there were no longer any values ​​in the sequence. By limiting the interval, we make the whole task smaller. Now consider the sliding property: move the window one position to the right, and get another subsequence, to which processing can also be applied.

And here begins our adventure. If we apply the algorithm to each window individually, then as a result we will get brute force tactics.

However, the beauty of the sliding window method lies in the fact that it allows you to change the structure of the algorithm so that it takes advantage of the window shift process itself . And the goal of all this is to create better and faster algorithms.

We can increase the execution speed of almost any algorithm applied to a sliding window, at least theoretically. When you shift the window, only two elements change. The oldest one drops out and the newest one falls into the frame.


Figure 2. Element shift (red: dropped out, green: arrived)

If rough search requires ksteps to process one window long k, and there are nwindows in the sequence , then the rough search algorithm will take n·ksteps to complete the work . But since only two elements change at each step, we can achieve a total execution time that is approximately proportional 2n.

If we say that a simple passage through a sequence takes time O(n), then this means that on an overall sequence no algorithm can be faster thanO(n). This analysis showed us that the correct application of the sliding window method can lead to the invention of algorithms for processing complete sequences that can be executed in time O(n).

In other words, he promises us that we can invent algorithms that are ideal for solving the problem, which cannot be faster!

Having finished with the necessary introduction, we will consider three programming problems that can be solved with the help of this general concept of algorithms, and show specific examples of how they were used in real cases.

Programming Objective 1: Moving Average

The problem that needs to be solved: create an algorithm that calculates the moving average of a number series.

For a given series a0, a1, … an-1and parameter, k, 0 < k <= nwe must generate a new sequence, such that each element is the average value of the ksuccessive elements of the original sequence:


Figure 3. Eq Average

Context: a moving average is useful for smoothing the input stream. If the numbers are affected by noise, then raw data will be difficult to display. As can be seen from the two illustrations below, smoothing allows you to get a more informative scheme.


Figure 4. A moving average smooths the input data.

This problem can be effectively solved using the sliding window method. It immediately reveals a common feature of most of these algorithms: the first k-1elements do not produce output. Only when filling the entire window we can get the first portion of the results. All subsequent windows create one result each. Therefore, a sequence of nelements when using the sliding window algorithm creates a sequence of n-k+1results.

Now let's move on to implementation. The average value of a window is the sum of all elements divided by the length of the window.


Figure 5. Eq Sum

With this formulation, we can immediately see the advantage of using the sliding window method. The sum of the window values ​​can be calculated from the sum of the values ​​of the window preceding it:


Figure 6. Eq Optimization

Calculating the sum of the first window will take ksteps, and for each next window only two additional operations are required.

The following is a C ++ implementation of this answer, passing the first kelements to create the first output. All other output numbers are calculated using an optimized summation formula.

double* moving_average(double* data, int n, int k)
{
   assert(data != NULL);
   assert(n > 0);
   assert(0 < k && k <= n);
   double* result = new double[n — k + 1];
   double sum = 0;
   for (int i = 0; i < k; i++)
   {
      sum += data[i];
   }
   result[0] = sum / k;
   for (int i = k; i < n; i++)
   {
      sum = sum — data[i — k] + data[i];
      result[i — k + 1] = sum / k;
   }
   return result;
}

The main point of this algorithm is that each element in the original sequence is processed a maximum of twice, which creates a general time complexity O(n).

Programming Problem 2: Subsequence with Maximum Sum

The problem that needs to be solved: to create an algorithm for finding subsequences with the largest sum of all possible subsequences.

This can be a real problem if the input contains negative values.

And here again, you can use the sliding window method to create a solution with runtime O(n). Only this time the window length will not be constant. In fact, since the task itself is to find the most suitable window, the length of the window may change in the process.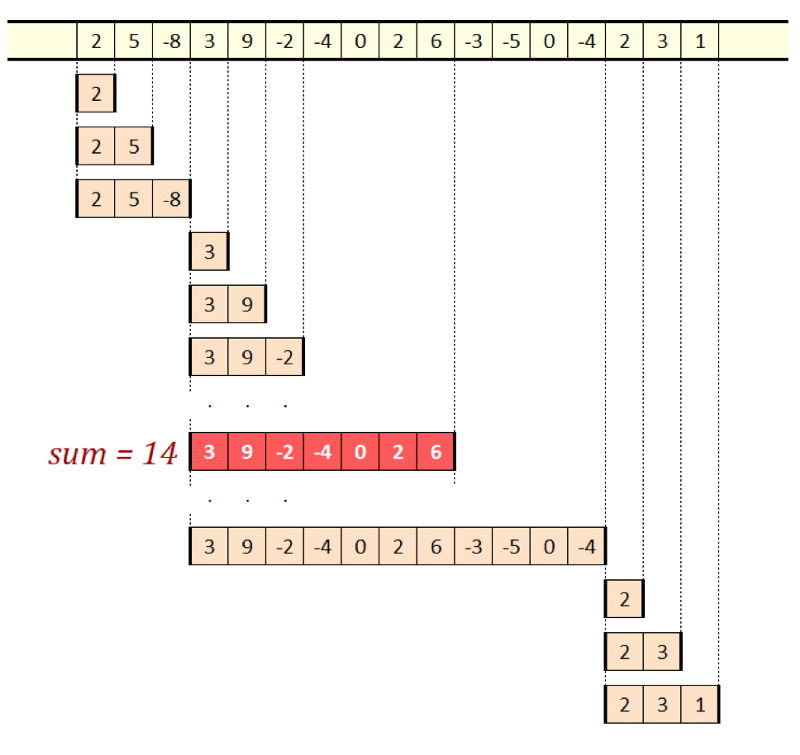


Figure 7. Maximum amount, a solution with sliding windows.

The idea is to watch what happens when we already have a window with a certain amount. Then we want to add the following value. This value can be added to the sum of the window. But it can be taken as a completely new window of unit length. Ask a question: which of them will have a larger amount? Whatever it is, we will save it as a new window and move to the next input value by repeating the same procedure. Look at the picture above, which shows how windows gradually slide along the sequence.

The winning option will always be a subsequence with a maximum amount ending at the current input element. Each window is discarded immediately when its sum becomes negative: this is a situation in which the number alone is better than in combination with the maximum window preceding it.

We have only one last step left - the determination of the total maximum. All windows are candidates because they glide toward the end of the sequence. After completion of the sequence, the window with the largest amount will be the subsequence with the maximum amount.

The following is a straightforward implementation of the algorithm in C ++. And again, each element of the sequence is considered no more than two times, which is the total time complexity of the function O(n).

std::tuple max_sum_subsequence(int* data, int n)
{
   assert(data != NULL);
   assert(n > 0);
   int bestStart = 0;
   int bestLength = 1;
   int maxSum = data[0];
   int curStart = bestStart;
   int curLength = bestLength;
   int curSum = maxSum;
   for (int i = 1; i < n; i++)
   {
     if (curSum < 0)
     {
       curStart = i;
       curLength = 1;
       curSum = data[i];
     }
     else
     {
       curLength += 1;
       curSum += data[i];
     }
     if (curSum > maxSum)
     {
       bestStart = curStart;
       bestLength = curLength;
       maxSum = curSum;
     }
   }
   return std::tuple(bestStart, bestLength, maxSum);
}

Programming Problem 3: Maxima of All k-subsequences

Problem to be solved: create an algorithm that calculates the maxima of all subsequences of length kin a numerical sequence of length n. Note: this is a difficult task.

This algorithm is used in image processing, where, as you might guess, algorithms with runtime O(n)are valued the most.


Figure 8. Maximums

When a window slides, it creates the maximum contained value at the output. The hard part of the solution is that there is no formula that gives the maximum of a given window. We can take one of the elements as a result.

But we cannot say that we cannot benefit from the use of the sliding window method. This is what the idea is: suppose we have a window with four values, as shown in the figure above.

When an additional value falls into the frame, we need to understand how it relates to the existing values. To begin with, when the window continues to slide, all previous values ​​drop out of it before this new value drops out. This is an important conclusion. If the previous value is less than the new, then it will never become a maximum, simply because the new, larger value will always overshadow it.


Figure 9 Sliding the maximum

This leads us to the idea of ​​not recognizing each new value and deleting all the smaller values ​​that it finds in the window when the window is sliding, as shown in the figure below. This operation has a different consequence.

If each value added to the right deletes ever smaller values, then the window will contain only the non-increasing, discontinuous subsequence of the original window. Another consequence is that it is now becoming obvious - the leftmost window element is the maximum value that we need to calculate.


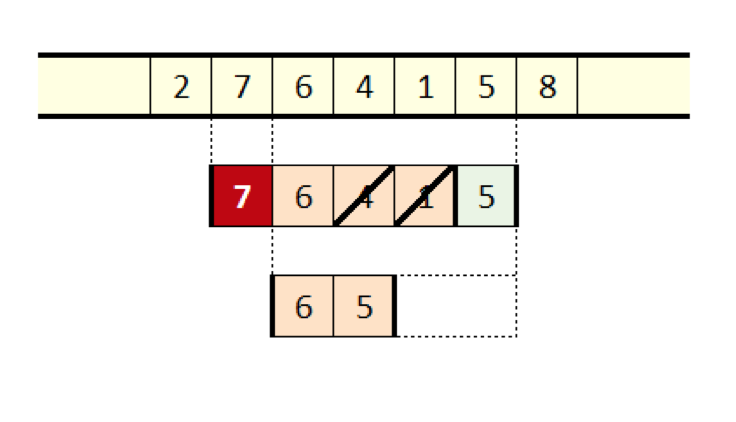
Figure 10. Maximum sifting.

One more detail needs to be clarified. When sliding the window, the leftmost value of the sequence drops out. This value could already be removed with a larger value. Or it could survive all the values ​​following it on the right. In the latter case, the value from the input will be the leftmost value in the frame, and now it is time to delete it.

The figure below shows the entire process applied to a sequence of seven elements with a window length of four.


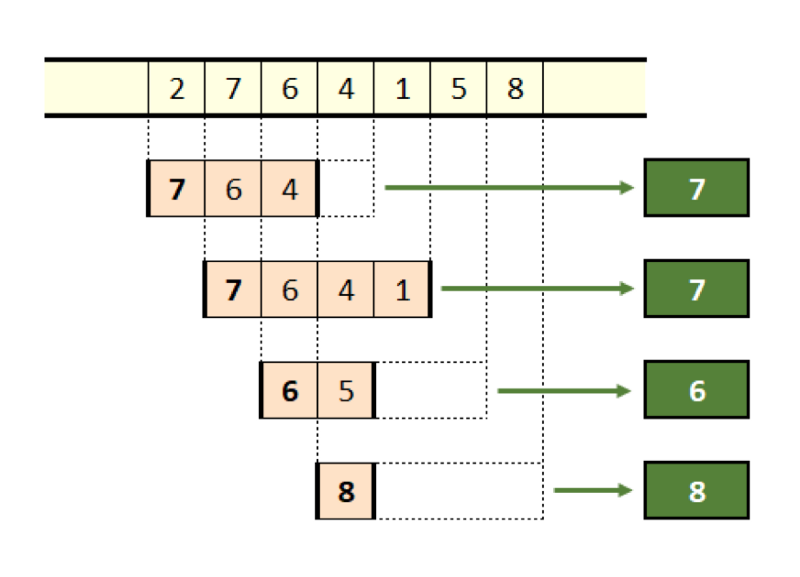
Figure 11. The maximums of everything

On this we will complete the description of the algorithm and begin its implementation. The usual implementation is based on a two-way queue (dequeue). Dequeue supports adding to and removing from the queue from both ends, and it is these operations that we use to implement the algorithm.

void insert_maximum_candidate(int value, bounded_deque &maximums)
{
   while (!maximums.empty() && maximums.back() < value)
           maximums.pop_back();
   maximums.push_back(value);
}
void remove_maximum_candidate(int value, bounded_deque &maximums)
{
   if (!maximums.empty() && maximums.front() == value)
        maximums.pop_front();
}
int* range_maximums(int* data, int n, int k)
{
   assert(data != NULL);
   assert(n > 0);
   assert(0 < k && k <= n);
   bounded_deque maximums(k);
   for (int i = 0; i < k — 1; i++)
        insert_maximum_candidate(data[i], maximums);
   int* result = new int[n — k + 1];
   for (int i = k — 1; i < n; i++)
   {
        insert_maximum_candidate(data[i], maximums);
        result[i — k + 1] = maximums.front();
        remove_maximum_candidate(data[i — k + 1], maximums);
   }
   return result;
}

In this solution, we use our own implementation of Dequeue called fixed_deque. In contrast std::deque, this class maintains a buffer for fixed-length data, which speeds up execution by at least one order of magnitude. Inside, it acts as a ring buffer, which is extremely efficient. Be that as it may, the class fixed_dequehas the same public interface as std::deque(the only difference is that its constructor expects a buffer size) and you can replace it with if you wish std::deque. Other than a significant reduction in execution speed, there will be no other consequences.

As in the previous examples, we can analyze the time complexity of this implementation. Each value from the input sequence is subjected to queuing and removal from it no more than once. That is, a maximum of two operations are performed on one input number, and the total time complexity of the algorithm is equal O(n). Also, this algorithm requires additional space O(k), where k is the window length. (It is worth noting that previous algorithms only needed O(1)space.)

Think outside the box

We examined three algorithms based on the sliding window method. As we promised, each of them runs in time O(n). I would also like to show you how the same method is applied in two completely different areas.

First, in packet routing protocols, such as TCP / IP, a sliding window is used to negotiate Internet Protocol (IP) with Transmission Control Protocol (TCP). IP can never guarantee that packets will be received in the same order in which they were sent. At the same time, TCP just provides this guarantee. Here, a sliding window becomes one of the most important components of the success of the TCP / IP protocol bundle.

The TCP receiver maintains a window of expected packets. Packets arrive at a less perfect (but more realistic) IP, and may not arrive in the order necessary to fill the corresponding window positions. However, as soon as the leftmost packet arrives, the TCP window shifts to the right as much as possible, confirms to the sender the receipt of all adjacent packets and sends them to the exit. This, in turn, signals the sender about the possibility of starting the transmission of subsequent packets to the IP network.


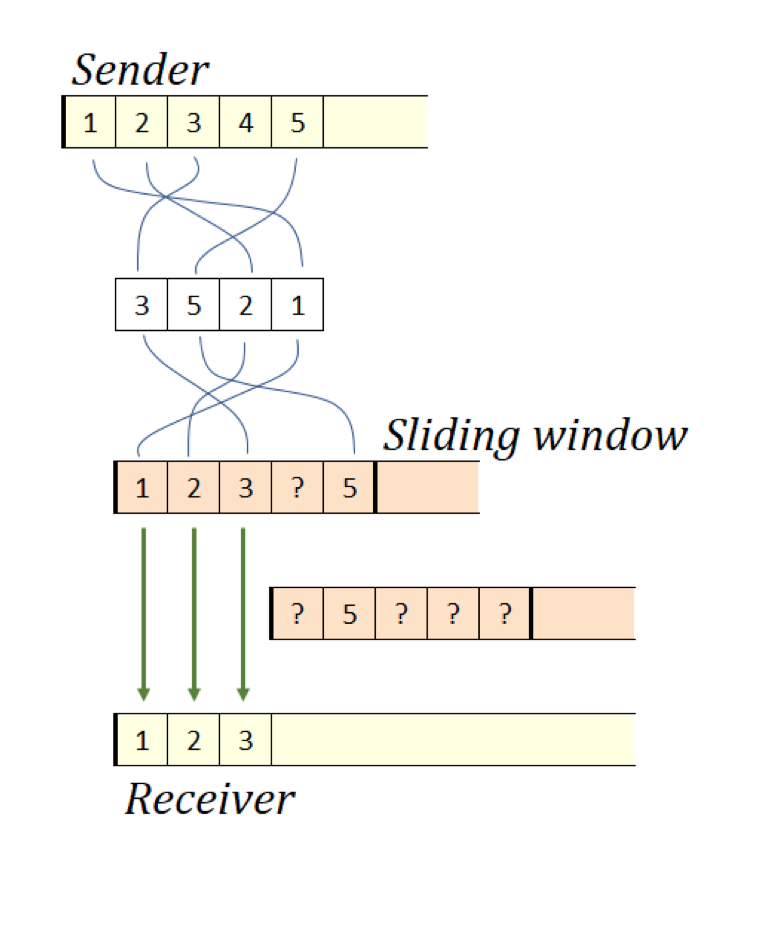
Figure 12. TCP-IP

You have already guessed what the second (and last) example will be devoted to.

Of course, "Snake . " When this game appeared several decades ago, most knew it from Nokia cell phones.


Figure 13. Snake

Guess? The snake itself is a sliding window! When the snake moves, it’s enough for us to draw only two blocks on the screen - the tail becomes the background block, and the former background in front of the snake’s head becomes a new head.


Figure 14. “Snake” = sliding window

The result of applying the sliding window method was that each frame of the game costs us to draw a maximum of two primitive blocks, regardless of the length of the snake. This allowed you to implement the game on a primitive hardware without unnecessary battery consumption.

To summarize

In this article, we have analyzed a general algorithm called a sliding window. You have learned that this technique can be used to optimize data sequence processing algorithms. With a successful application, the technique provides the creation of algorithms that run in time O(n)for a sequence of n objects, which is the most optimal design of algorithms.

As specific examples of problem solving, we have developed three different algorithms that work with numerical sequences. All these algorithms are used in the real world to process common data and image processing. This explains why the sliding window method has survived to this day and remains a useful tool in creating algorithms. Therefore, you will most likely hear about him at technical interviews.