Implementing the Bailey – Borwain – Pluff Algorithm on Golang

_{Number Pi, I tell you brothers,
It’s easier to remember that.
Three fourteen fifteen
Nine two, six five, three five.
© Dmitry Eyt}

Recently I needed the number Pi in hexadecimal format. Approximately 10,000 decimal places. However, all publications on the network typically display Pi in decimal form. Having stumbled a bit, I found Pi in binary form, and it more than suited me: a simple conversion solved the tasks. Here it would end the story, but as they say, "a spoon was found, but the sediment remained." Below you can see a simple implementation of the PiHex library that generates a digit, or a sequence of digits in any position after the decimal point of the Pi number (though no more than 10,000,000).

So, there is an “BBP” algorithm that allows you to calculate the hexadecimal Pi character at any position after the decimal point. This algorithm itself is from the category of “crane” ones, more details about this family of algorithms can be found in the article: “Kranik”, or an algorithm for searching for digits of the Pi number . There was also an article on the implementation of the BBP algorithm in the C language on the Habré: Calculation of the Nth sign of the Pi number without calculating the previous ones

About the algorithm

The description of the algorithm is best read in the article “The BBP Algorithm for Pi” published by David Bailey on September 17, 2006: www.davidhbailey.com/dhbpapers/bbp-alg.pdf By the way, it is written quite understandably, at least not as a mathematician can also understand something. It can be seen from the article that the calculation uses a not very complicated formula in the form:

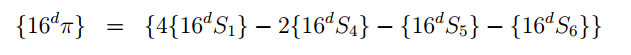
in this case, S _{j is} calculated as:

as a result, a slightly more cumbersome formula is obtained

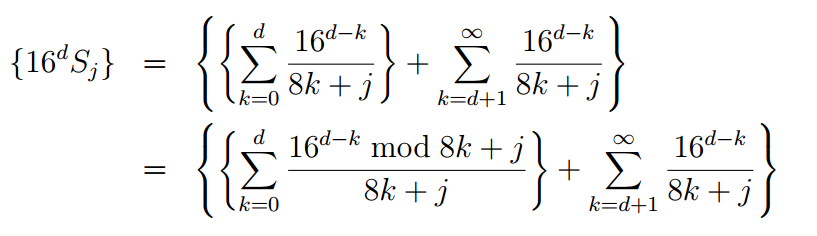
Implementation

When porting to Go, implementation was implemented using goroutin to parallelize the computationally intensive S _j . This made it possible to significantly speed up the calculations, since on modern computers there are usually more than one core in a processor. However, it is possible that this is not strong and is necessary if one character is required, but if it is a thousand, the speed of work will be important in any case.

API

Using the library is not easy, but very simple, because in fact, it supports only one method. The example below shows how to connect the library and get the first 20 decimal places:

package main
import (
    "fmt"
    "github.com/claygod/PiHex"
)
func main() {
    pi := PiHex.New()
    fmt.Print("The first 20 digits of Pi (hexadecimal): ", pi.Get(0, 20))
}

Where is the PiHex library useful

Actually, where Pi is needed, and at the same time in hexadecimal form. If large orders are required, then it may make sense to calculate Pi in advance and / or use the already calculated results, since for example, on my computer, calculating ten characters after 1,000,000 positions took a little more than ten seconds. Due to the limit of 10,000,000 decimal places, the PiHex library is in no way suitable for setting new records in the calculation of Pi.

Configuration

Actually, you can only change one parameter: STEP. It indicates how many digits can be computed per iteration. The default value is 9, and this is the maximum possible number that allows you to maintain the correctness of the calculated result. If in doubt, the number can be reduced, which is true, will reduce the speed of the library.

Testing

Since the API of the library is more than simple, I hope I was able to cover all possible holes in the library in the tests. And yes, when I wrote tests, holes were found, it could not have done without it.

References

PiHex Library at Github
Bailey- Borwain-Puff Formula
David Bailey's BBP Algorithm