Reservoir Sampling Algorithm
Reservoir sampling (eng. “Reservoir sampling”) is a simple and effective algorithm for randomly selecting a certain number of elements from the existing vector of large and / or unknown size in advance. I did not find a single article about this algorithm on Habré and therefore I decided to write it myself.
So, what is at stake. Selecting one random element from a vector is an elementary task:
The task of “returning K random elements from a vector of size N” is already trickier. Here you can make a mistake - for example, take the K first elements (this will violate the requirement of randomness) or take each of the elements with a probability of K / N (this will violate the requirement to take exactly K elements). In addition, it is possible to implement a formally correct, but extremely inefficient solution to “randomly mix all the elements and take the first K”. And everything becomes even more interesting if we add the condition that N is a very large number (we don’t have enough memory to save all N elements) and / or it is not known in advance. For example, imagine that we have some kind of external service that sends us items one by one. We do not know how many of them will come in and cannot save them all, but we want at any time to have a set of exactly K randomly selected elements from those already received.
The reservoir sampling algorithm allows solving this problem in O (N) steps and O (K) memory. In this case, it is not necessary to know N in advance, and the condition of randomness of a sample of exactly K elements will be clearly observed.
Let K = 1, i.e. we need to select only one element from all those who came - but so that each of the elements that came in had the same probability of being selected. The algorithm suggests itself:
Step 1 : Allocate memory for exactly one element. We keep in it the first incoming item.

As long as everything is OK - we have only one element, with a probability of 100% (at the moment) it should be selected - it is.
Step 2 : We rewrite the second incoming element with a probability of 1/2 as the selected one.

Here, too, everything is fine: for the time being, only two elements have arrived. The first one remained selected with a probability of 1/2, the second re-recorded it with a probability of 1/2.
Step 3 : The third incoming element with probability 1/3 is overwritten as the selected one.
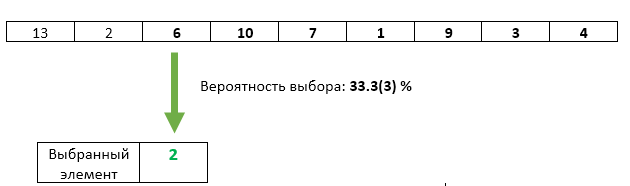
With the third element, everything is fine - his chance of being selected is exactly 1/3. But have we not violated in any way the equality of the chances of the previous elements? Not. The probability that in this step the selected item will not be overwritten is 1 - 1/3 = 2/3. And since in step 2 we guaranteed equal chances of each of the elements to be selected, then after step 3 each of them can be selected with a chance of 2/3 * 1/2 = 1/3. Exactly the same chance as the third element.
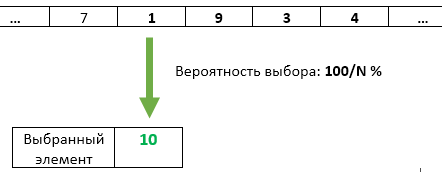
Step N : With a probability of 1 / N, item number N is overwritten as the selected one. Each of the previous incoming items has the same 1 / N chance to remain selected.
But it was a simplified task, with K = 1.
Step 1 : Allocate memory for K items. Write the first K elements in it.

The only way to take K elements from K incoming elements is to take them all :)
Step N : (for each N> K): generate a random number X from 1 to N. If X> K then discard this element and proceed to the next. If X <= K, then we overwrite the element with the number X. Since the value of X will be uniformly random on the range from 1 to N, then under the condition X <= K it will be uniformly random and on the range from 1 to K. Thus, we ensure uniformity select rewritable items.

As you can see, each next incoming element has a lower and lower probability of being selected. However, it will always be equal to exactly K / N (as for each of the previous incoming elements).
The advantage of this algorithm is that we can stop at any time, show the user the current vector K - and this will be the vector of honestly selected random elements from the incoming sequence of elements. Perhaps the user is satisfied, and perhaps he wants to continue processing incoming values - we can do this at any time. In this case, as mentioned at the beginning, we never use more than O (K) memory.
Oh yeah, I completely forgot, the std :: sample function is finally included in the standard C ++ 17 library.that does exactly what is described above. The standard does not oblige it to use exactly the tank sample, but it does oblige to work in O (N) steps - well, the developers of its implementation in the standard library will hardly choose any algorithm that uses more than O (K) memory (and less will not work either) - the result must be stored somewhere).
So, what is at stake. Selecting one random element from a vector is an elementary task:
// C++std::random_device rd;
std::mt19937 gen(rd());
std::uniform_int_distribution<> dis(0, vect.size() — 1);
auto result = vect[dis(gen)];
The task of “returning K random elements from a vector of size N” is already trickier. Here you can make a mistake - for example, take the K first elements (this will violate the requirement of randomness) or take each of the elements with a probability of K / N (this will violate the requirement to take exactly K elements). In addition, it is possible to implement a formally correct, but extremely inefficient solution to “randomly mix all the elements and take the first K”. And everything becomes even more interesting if we add the condition that N is a very large number (we don’t have enough memory to save all N elements) and / or it is not known in advance. For example, imagine that we have some kind of external service that sends us items one by one. We do not know how many of them will come in and cannot save them all, but we want at any time to have a set of exactly K randomly selected elements from those already received.
The reservoir sampling algorithm allows solving this problem in O (N) steps and O (K) memory. In this case, it is not necessary to know N in advance, and the condition of randomness of a sample of exactly K elements will be clearly observed.
Let's start with a simplified task.
Let K = 1, i.e. we need to select only one element from all those who came - but so that each of the elements that came in had the same probability of being selected. The algorithm suggests itself:
Step 1 : Allocate memory for exactly one element. We keep in it the first incoming item.

As long as everything is OK - we have only one element, with a probability of 100% (at the moment) it should be selected - it is.
Step 2 : We rewrite the second incoming element with a probability of 1/2 as the selected one.

Here, too, everything is fine: for the time being, only two elements have arrived. The first one remained selected with a probability of 1/2, the second re-recorded it with a probability of 1/2.
Step 3 : The third incoming element with probability 1/3 is overwritten as the selected one.

With the third element, everything is fine - his chance of being selected is exactly 1/3. But have we not violated in any way the equality of the chances of the previous elements? Not. The probability that in this step the selected item will not be overwritten is 1 - 1/3 = 2/3. And since in step 2 we guaranteed equal chances of each of the elements to be selected, then after step 3 each of them can be selected with a chance of 2/3 * 1/2 = 1/3. Exactly the same chance as the third element.
Step N : With a probability of 1 / N, item number N is overwritten as the selected one. Each of the previous incoming items has the same 1 / N chance to remain selected.

But it was a simplified task, with K = 1.
How does the algorithm change when K> 1?
Step 1 : Allocate memory for K items. Write the first K elements in it.

The only way to take K elements from K incoming elements is to take them all :)
Step N : (for each N> K): generate a random number X from 1 to N. If X> K then discard this element and proceed to the next. If X <= K, then we overwrite the element with the number X. Since the value of X will be uniformly random on the range from 1 to N, then under the condition X <= K it will be uniformly random and on the range from 1 to K. Thus, we ensure uniformity select rewritable items.

As you can see, each next incoming element has a lower and lower probability of being selected. However, it will always be equal to exactly K / N (as for each of the previous incoming elements).
The advantage of this algorithm is that we can stop at any time, show the user the current vector K - and this will be the vector of honestly selected random elements from the incoming sequence of elements. Perhaps the user is satisfied, and perhaps he wants to continue processing incoming values - we can do this at any time. In this case, as mentioned at the beginning, we never use more than O (K) memory.
Oh yeah, I completely forgot, the std :: sample function is finally included in the standard C ++ 17 library.that does exactly what is described above. The standard does not oblige it to use exactly the tank sample, but it does oblige to work in O (N) steps - well, the developers of its implementation in the standard library will hardly choose any algorithm that uses more than O (K) memory (and less will not work either) - the result must be stored somewhere).
Materials on the topic
- Facebook developer report on how tank sampling was used in their search engine by internal code base (from the 34th minute).
- Wikipedia article
- std :: sample on Cppreference
