Modeling Dynamic Systems: How does the moon move?
- Tutorial
The blessed memory of my teacher - the first dean of the Faculty of Mathematics and Physics of the Novocherkassk Polytechnic Institute, Head of the Department "Theoretical Mechanics" Alexander N. Kabelkov
August, summer is coming to an end. People violently rushed to the sea, but it is not surprising - the season. And on Habré, meanwhile, with pompous color it dissolves and smells of pseudoscience . If we talk about the topic of this issue of "Modeling ...", then we will combine the pleasant with the useful in it - we will continue the promised cycle and just a bit more will fight with this very pseudoscience for the inquisitive minds of modern youth.

And the question is really not idle - from school years we used to think that our closest satellite in outer space - the Moon moves around the Earth with a period of 29.5 days, especially without going into the accompanying details. In fact, our neighbor is a peculiar and to some extent unique astronomical object, with the movement of which around the Earth is not so simple as it might have been desirable for some of my colleagues from the near abroad.
So, leaving the controversy aside, we will try from different sides, to the best of our competence, to consider this unconditionally beautiful, interesting and very revealing task.
Discovered in the second half of the 17th century, by Sir Isaac Newton, the law of universal perception speaks of the fact that the moon is attracted to the Earth (and the Earth to the Moon!) With a force directed along the straight line connecting the centers of the considered celestial bodies and equal to
where m 1 , m 2 are the masses, respectively, of the Moon and the Earth; G = 6.67e-11 m 3 / (kg * s 2 ) - gravitational constant; r 1,2- the distance between the centers of the moon and the earth. If we take into account only this force, then, having solved the problem of the motion of the Moon as a satellite of the Earth and having learned to calculate the position of the Moon in the sky against the background of stars, we will soon be convinced by direct measurements of the equatorial coordinates of the Moon that in our conservatory not everything is as smooth as I would like to. And the point here is not in the law of universal perception (and in the early stages of the development of celestial mechanics such thoughts were expressed quite often), but in unaccounted perturbation of the motion of the moon by other bodies. What kind? We look at the sky and our gaze immediately rests on a hefty, weighing as much as 1.99e30 kilograms plasma ball right under our nose - the Sun. Is the moon attracted to the sun? More like, with a force equal in magnitude
where m 3 is the mass of the Sun; r 1,3 is the distance from the moon to the sun. Compare this force with the previous one.
Take the position of the bodies, in which the attraction of the Moon to the Sun will be minimal: all three bodies are on one straight line and the Earth is located between the Moon and the Sun. In this case, our formula will look like:
Where , m - the average distance from the Earth to the Moon;
, m - the average distance from the Earth to the Moon;  , m - the average distance from the Earth to the Sun. Substitute the real parameters in this formula
, m - the average distance from the Earth to the Sun. Substitute the real parameters in this formula
Here is the number! It turns out that the Moon is attracted to the Sun by a force that is more than two times greater than the force of its attraction to the Earth.
Such a disturbance can no longer be ignored, and it will definitely affect the final trajectory of the Moon. Let us go further, taking into account the assumption that the Earth’s orbit is circular with radius a, we find the locus of points around the Earth, where the force of attraction of any object to the Earth is equal to the force of its attraction to the Sun. This will be a sphere with a radius
displaced along a straight line connecting the Earth and the Sun in the opposite direction to the Sun at a distance
Where - The ratio of the mass of the earth to the mass of the sun. Substituting the numerical values of the parameters, we obtain the actual dimensions of this area: R = 259300 kilometers, and l = 450 kilometers. This area is called the sphere of the Earth's gravity relative to the sun .
- The ratio of the mass of the earth to the mass of the sun. Substituting the numerical values of the parameters, we obtain the actual dimensions of this area: R = 259300 kilometers, and l = 450 kilometers. This area is called the sphere of the Earth's gravity relative to the sun .
The known orbit of the moon lies outside this area. That is, at any point of the trajectory, the Moon suffers from the Sun significantly more attraction than from the Earth.
This information often gives rise to disputes that the Moon is not a satellite of the Earth, but an independent planet of the Solar System, whose orbit is outraged by the attraction of the near Earth.
Let us estimate the perturbation introduced by the Sun into the trajectory of the Moon relative to the Earth, as well as the disturbance introduced by the Earth into the trajectory of the Moon relative to the Sun, using the criterion proposed by P. Laplace. Consider three bodies: the Sun (S), the Earth (E) and the Moon (M).
Let us assume that the orbits of the Earth relative to the Sun and the Moon relative to the Earth are circular.
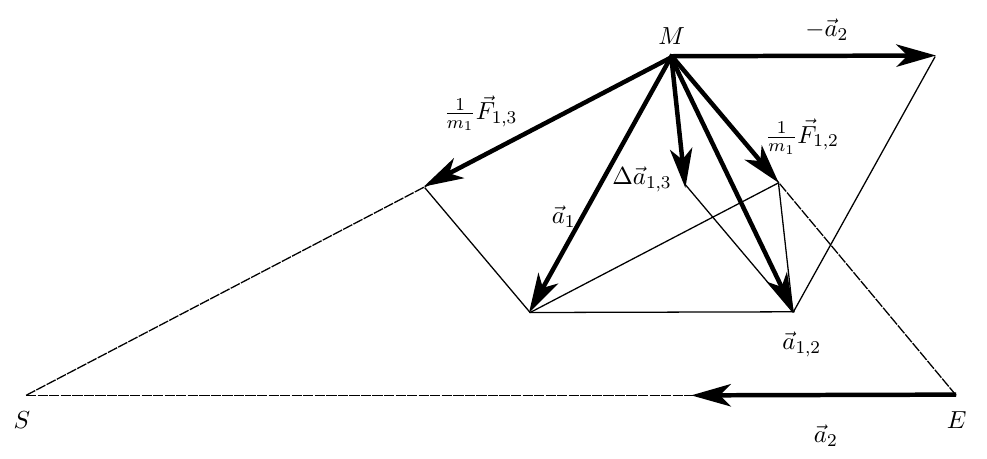
Consider the motion of the moon in a geocentric inertial frame of reference. The absolute acceleration of the moon in the heliocentric reference system is determined by the forces acting on it and is equal to:
On the other hand, according to the Coriolis theorem, the absolute acceleration of the moon
Where - portable acceleration equal to the acceleration of the Earth relative to the Sun;
- portable acceleration equal to the acceleration of the Earth relative to the Sun;  - acceleration of the moon relative to the earth. Accelerations of Coriolis will not be here - the chosen coordinate system moves progressively. From here we get the acceleration of the moon relative to the earth.
- acceleration of the moon relative to the earth. Accelerations of Coriolis will not be here - the chosen coordinate system moves progressively. From here we get the acceleration of the moon relative to the earth.
A portion of this acceleration equal to due to the attraction of the Moon to the Earth and characterizes its undisturbed geocentric movement. Remaining part
due to the attraction of the Moon to the Earth and characterizes its undisturbed geocentric movement. Remaining part
the acceleration of the moon caused by disturbance from the sun.
If we consider the motion of the moon in the heliocentric inertial reference frame, then everything is much simpler, the acceleration characterizes the undisturbed heliocentric motion of the moon, and the acceleration
characterizes the undisturbed heliocentric motion of the moon, and the acceleration  - outrage of this movement from the Earth.
- outrage of this movement from the Earth.
With the parameters of the orbits of the Earth and the Moon existing in the current epoch, the inequality is true at each point of the trajectory of the Moon
which can be verified by direct calculation, but I refer to the source in order not to overly clutter the article.
What does inequality (1) mean? Yes, the fact that in relative terms the effect of the perturbation of the Moon by the Sun (and very significantly) is less than the effect of the attraction of the Moon to the Earth. And vice versa, the Earth's perturbation of the geoliocentric trajectory of the Moon has a decisive influence on the nature of its movement. The influence of the earth's gravity in this case is more significant, which means the moon "belongs" to the earth by right and is its satellite.
Another interesting thing is that by turning inequality (1) into an equation, you can find the locus of points where the effects of perturbations of the Moon (and any other body) by the Earth and the Sun are the same. Unfortunately, this is not so easy as in the case of the realm of the sphere. Calculations show that this surface is described by an equation of crazy order, but close to an ellipsoid of revolution. All that we can do without unnecessary problems is to assess the overall dimensions of this surface relative to the center of the Earth. Numerically solving the equation
relative to the distance from the center of the Earth to the desired surface on a sufficient number of points, we obtain the cross section of the desired surface by the ecliptic plane
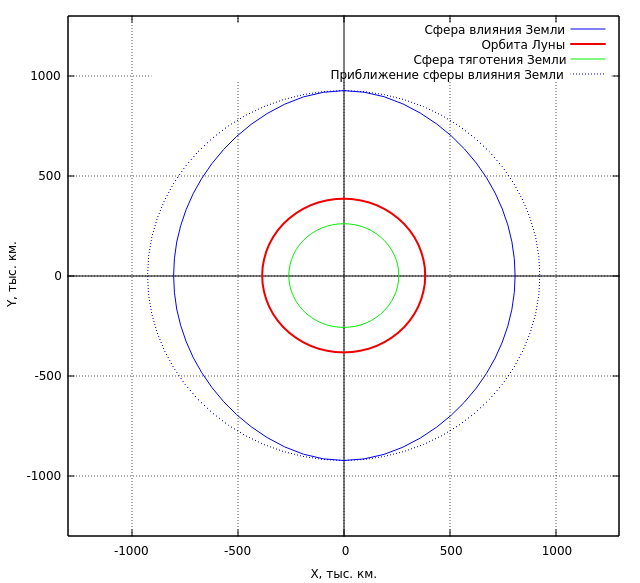
For clarity, the geocentric orbit of the moon is shown here, and the sphere we found above is relative to the sun. It can be seen from the figure that the sphere of influence, or the sphere of the gravitational action of the Earth relative to the Sun, is the surface of rotation about the X axis, flattened along the straight line connecting the Earth and the Sun (along the axis of eclipses). The moon's orbit is deep inside this imaginary surface.
For practical calculations, this surface is conveniently approximated by a sphere with a center in the center of the Earth and a radius equal to
where m is the mass of a smaller celestial body; M is the mass of the larger body, in the field of which the smaller body moves; a - the distance between the centers of bodies. In our case
This unfinished million kilometers is the theoretical limit beyond which the power of the old woman of the Earth does not extend - its influence on the trajectories of astronomical objects is so small that it can be neglected. So, to launch the Moon in a circular orbit at a distance of 38.4 million kilometers from the Earth (as some linguists do) does not work, it is physically impossible.
This sphere, for comparison, is shown in the figure by a blue dashed line. At estimated calculations, it is considered that the body inside this sphere will experience only from the side of the Earth. If the body is outside this sphere, we believe that the body moves in the field of the sun. In practical cosmonautics, a method of conjugation of conic sections is known, which makes it possible to approximately calculate the trajectory of a spacecraft using the solution of the two-body problem. In this case, all the space that the apparatus overcomes is divided into similar spheres of influence.
For example, it is now clear that in order to have a theoretical opportunity to perform maneuvers for entering a circumlunar orbit, the spacecraft must fall within the sphere of the Moon’s action relative to the Earth. Its radius is easy to calculate by the formula (3) and it is equal to 66 thousand kilometers.
Thus, the moon can rightly be considered a satellite of the Earth. However, due to the significant influence of the gravitational field of the Sun, it does not move in the central gravitational field, which means its trajectory is not a conic section.
So, we will consider a model problem in a general formulation, known in celestial mechanics as a three-body problem. Consider three bodies of arbitrary mass, arranged arbitrarily in space and moving exclusively under the action of forces of mutual gravitational attraction
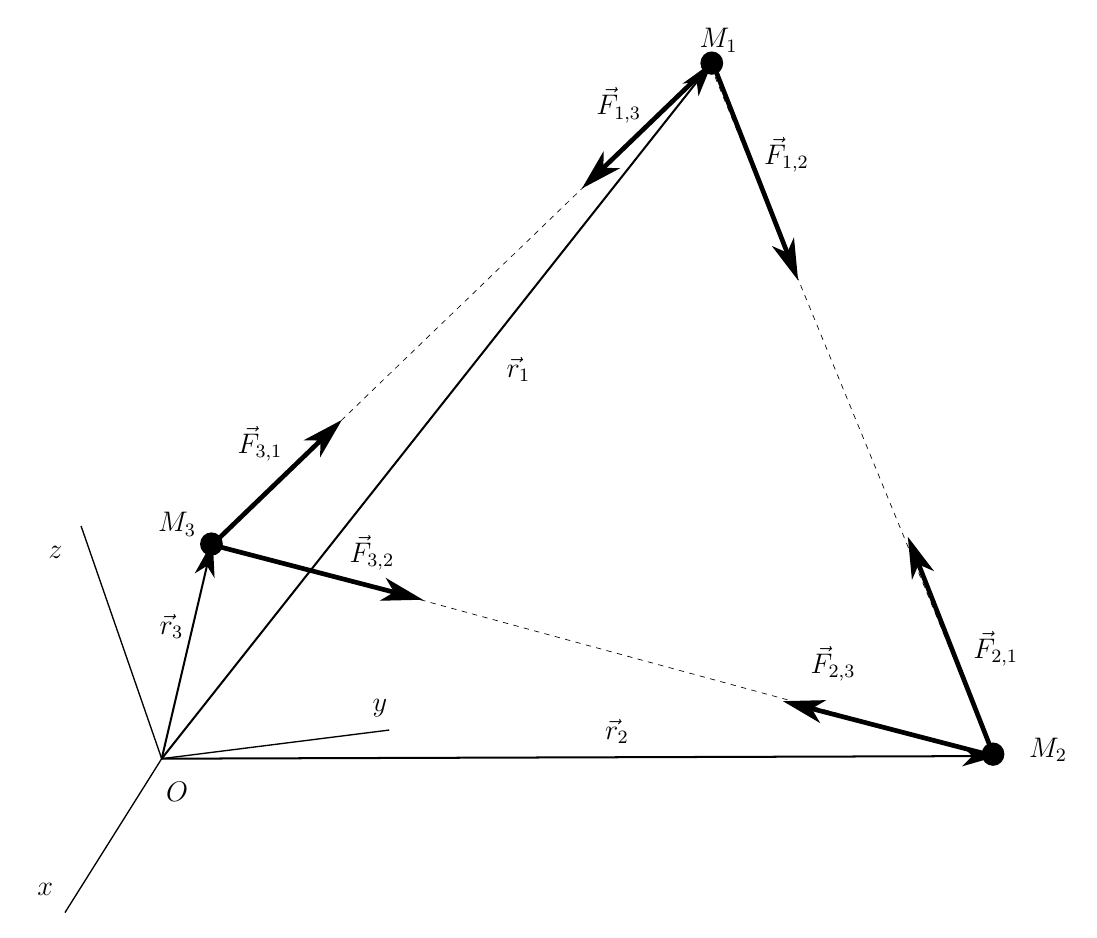
The bodies are considered material points. The position of the bodies will be counted in an arbitrary basis, which is associated with the inertial reference system Oxyz . The position of each of the bodies is given by the radius vector, respectively ,
,  and
and  . Each body is affected by the force of gravitational attraction from the other two bodies, and in accordance with the third axiom of the dynamics of a point (Newton's 3rd law)
. Each body is affected by the force of gravitational attraction from the other two bodies, and in accordance with the third axiom of the dynamics of a point (Newton's 3rd law)
We write the differential equations of motion of each point in vector form.
or, taking into account (4)
In accordance with the law of the world, the interaction forces are directed along the vectors
Along each of these vectors we will release the corresponding ort
then each of the gravitational forces is calculated by the formula
Given all this, the system of equations of motion takes the form
We introduce the notation adopted in celestial mechanics.
- gravitational parameter of the attracting center. Then the equations of motion will take the final vector view.
A fairly popular technique in mathematical modeling is to reduce differential equations and other relations describing the process to dimensionless phase coordinates and dimensionless time. Other parameters are also normalized. This allows us to consider, albeit with the use of numerical modeling, but in a fairly general form a whole class of typical tasks. I leave the question of how justified this is in each solvable problem, but I agree that in this case, this approach is quite fair.
So, we introduce some abstract celestial body with a gravitational parameter such that the orbital period of the satellite in an elliptical orbit with the major semiaxis
such that the orbital period of the satellite in an elliptical orbit with the major semiaxis  around it is equal
around it is equal  . All these quantities, by virtue of the laws of mechanics, are related by
. All these quantities, by virtue of the laws of mechanics, are related by
We introduce the replacement of parameters. For the position of the points of our system
Where - dimensionless radius vector of the i-th point;
- dimensionless radius vector of the i-th point;
for gravity body parameters
Where - dimensionless gravitational parameter of the i-th point;
- dimensionless gravitational parameter of the i-th point;
for time
Where - dimensionless time.
- dimensionless time.
Now recalculate the acceleration points of the system through these dimensionless parameters. Let's apply direct double differentiation in time. For speeds
For acceleration
When substituting the obtained relations into the equations of motion, everything elegantly collapses into beautiful equations:
This system of equations is still considered non-integrable in analytic functions. Why is it considered and is not? Because the successes of the theory of the function of a complex variable led to the fact that the general solution of the three-body problem did appear in 1912 — Karl Sundman found an algorithm for finding coefficients for infinite series with respect to a complex parameter, which theoretically is a general solution of the three-body problem. But ... for the application of Zundman's series in practical calculations with the accuracy required for them, it requires obtaining such a number of members of these series that this task is much greater than the capabilities of computers even today.
Therefore, numerical integration is the only way to analyze the solution of equation (5)
As I wrote earlier , before starting the numerical integration, you should take care to calculate the initial conditions for the problem to be solved. In the problem under consideration, the search for initial conditions turns into an independent subtask, since system (5) gives us nine second-order scalar equations, which, when going to normal form, Cauchy increases the order of the system by another 2 times. That is, we need to calculate as many as 18 parameters — the initial positions and components of the initial velocity of all points of the system. Where do we get data on the position of the celestial bodies of interest to us? We live in a world where man walked on the moon - naturally, humanity must have information about how this moon moves and where it is located.
That is, you say, you, dude, offer us to take thick astronomical reference books from the shelves, blow dust from them ... They didn’t guess! I propose to go for these data to those who actually walked on the moon, to NASA, namely in the Jet Propulsion Laboratory, Pasadena, California. Here is the JPL Horizonts web interface .
Here, having spent some time studying the interface, we will get all the data we need. Choose a date, for example, yes we do not care, but let it be July 27, 2018 UT 20:21. Just at that moment there was a complete phase of the lunar eclipse. The program will give us a huge footwoman
Br-rr, what is it? Without panic, for someone who taught astronomy well at school, there is nothing to fear for mechanics and mathematics. So, the most important final search coordinates and components of the velocity of the moon.
Yes, yes, yes, they are Cartesian! If you carefully read the entire footcloth, then we learn that the origin of this coordinate system coincides with the center of the Earth. The XY plane lies in the plane of the earth's orbit (the plane of the ecliptic) for the epoch J2000. The X axis is directed along the line of intersection of the equatorial plane of the Earth and the ecliptic to the vernal equinox. The Z axis looks in the direction of the north pole of the Earth perpendicular to the plane of the ecliptic. Well, the Y axis complements all this happiness to the right three vectors. By default, the units of measurement of coordinates are astronomical units (the clever ones from NASA also give the value of the autronomic unit in kilometers). Speed units: astronomical units per day, day is assumed to be 86400 seconds. Full stuffing!
Similar information can be obtained for the Earth.
Here, the barycenter (center of mass) of the Solar system is chosen as the origin of coordinates. The data we are interested in
For the moon, we will need the coordinates and speed relative to the barycenter of the solar system, we can calculate them, or we can ask NASA to give us such data
Wonderful! Now it is necessary to slightly process the received data with a file.
To begin with, we will define the scale, because our equations of motion (5) are written in dimensionless form. The data provided by NASA themselves tell us that for the scale of the coordinates is to take one astronomical unit. Accordingly, as a reference body, to which we will ration the masses of other bodies, we take the Sun, and as the time scale, the period of the Earth’s orbit around the Sun.
All this is of course very good, but we did not set the initial conditions for the sun. “Why?” Some linguist would ask me. And I would say that the Sun is not motionless at all, but also rotates in its orbit around the center of mass of the Solar system. This can be seen by looking at the NASA data for the sun.
Looking at the RG parameter, we will see that the Sun rotates around the solar system barycenter, and on 07/27/2018, the center of the star is at a distance of one million kilometers. The radius of the sun, for reference - 696 thousand kilometers. That is, the barycenter of the solar system lies half a million kilometers from the surface of the star. Why? Yes, because all other bodies interacting with the Sun also inform him of the acceleration, mainly, of course, the heavy Jupiter. Accordingly, the Sun also has its own orbit.
Of course, we can choose these data as initial conditions, but no - we solve the three-body model problem, and Jupiter and other characters are not included in it. So to the detriment of realism, knowing the position and velocity of the Earth and the Moon, we recalculate the initial conditions for the Sun, so that the center of mass of the Sun-Earth-Moon system is at the origin. For the center of mass of our mechanical system, the equation
We place the center of mass at the origin, that is, let us set then
then
from where
We turn to the dimensionless coordinates and parameters by selecting
Differentiating (6) over time and moving to dimensionless time, we also obtain the ratio for the velocities
Where
Now we will write a program that will form the initial conditions in the “parrots” we have chosen. What will we write on? Of course on Python! After all, as you know, this is the best language for mathematical modeling.
However, if we get away from sarcasm, then we will really try a python for this purpose, and why not? I will definitely provide a link to all the code in my Github profile .
Program exhaust
Actually, the integration itself boils down to a more or less standard for SciPy procedure for preparing a system of equations: transforming an ODE system to the Cauchy form and calling the corresponding solver functions. To transform the system into a Cauchy form, we recall that
Then by entering the system state vector
we reduce (7) and (5) to one vector equation
To integrate (8) with the initial conditions, we write a little, quite a bit of code
Let's see what we did. The result was a spatial trajectory of the moon for the first 29 days from the chosen starting point.

as well as its projection into the ecliptic plane.

“Hey, uncle, what are you giving us?” It's a circle! ”
First, it’s not a circle - there is a noticeable shift in the projection of the trajectory from the origin to the right and down. Secondly - you notice nothing? No, well, really?
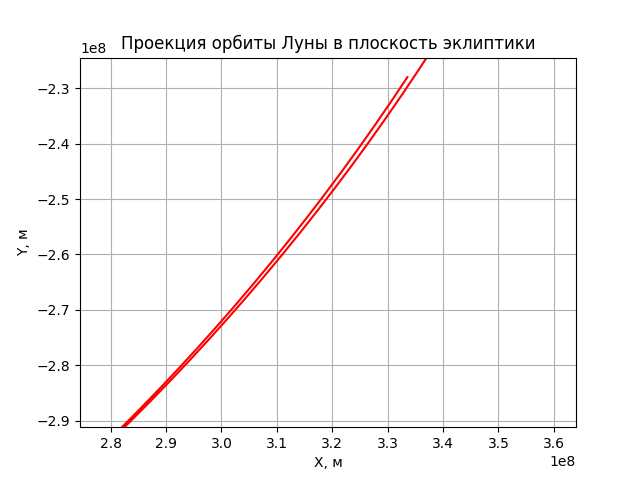
I promise to prepare a rationale for that (based on the analysis of the errors of the account and NASA data) that the resulting shift in the trajectory is not due to integration errors. While I suggest the reader to take my word for it - this shift is a consequence of the solar perturbation of the lunar trajectory. Spin one more turn


In both! And pay attention to the fact that, based on the initial data of the task, the Sun is just in that direction, where the trajectory of the Moon is shifted on each turn. Yes, this insolent Sun steals our favorite companion! Oh, this is the sun!
It can be concluded that solar gravity affects the moon's orbit quite significantly - the old woman does not walk twice through the sky in the same way. A picture for six months of movement allows (at least qualitatively) to make sure of this (the picture is clickable) Interesting? Still would. Astronomy is generally entertaining science.

In the university where I studied and worked for almost seven years - the Novocherkassk Polytechnic Institute - an annual student Olympiad on the theoretical mechanics of universities in the North Caucasus was held annually. Three times we took the All-Russian Olympiad. At the opening, our main "Olympian", Professor Kondratenko AI, always said: "Academician Krylov called mechanics the poetry of the exact sciences."
I love mechanics. All the good things that I have achieved in my life and career have happened thanks to this science and my wonderful teachers. I respect the mechanics.
Therefore, I will never allow anyone to scoff at this science and brazenly exploit it for their own purposes to anyone, even if it is at least three times a PhD and a linguist four times, and has developed at least a million training programs. I sincerely believe that writing articles on a popular public resource should provide for their careful reading, normal design (LaTeX formulas are not the whim of resource developers!) And the absence of errors leading to results that violate the laws of nature. The latter is generally a “must have”.
I often tell my students: “The computer frees your hands, but this does not mean that you need to turn off the brain as well.”
I also urge you, my dear readers, to appreciate and respect the mechanics. I will gladly answer any questions, and the source code of the example of solving the three-body problem in Python, as promised,I post it on my Github profile .
Thanks for attention!
Introduction
August, summer is coming to an end. People violently rushed to the sea, but it is not surprising - the season. And on Habré, meanwhile, with pompous color it dissolves and smells of pseudoscience . If we talk about the topic of this issue of "Modeling ...", then we will combine the pleasant with the useful in it - we will continue the promised cycle and just a bit more will fight with this very pseudoscience for the inquisitive minds of modern youth.

And the question is really not idle - from school years we used to think that our closest satellite in outer space - the Moon moves around the Earth with a period of 29.5 days, especially without going into the accompanying details. In fact, our neighbor is a peculiar and to some extent unique astronomical object, with the movement of which around the Earth is not so simple as it might have been desirable for some of my colleagues from the near abroad.
So, leaving the controversy aside, we will try from different sides, to the best of our competence, to consider this unconditionally beautiful, interesting and very revealing task.
1. The law of world wideness and what conclusions we can make of it
Discovered in the second half of the 17th century, by Sir Isaac Newton, the law of universal perception speaks of the fact that the moon is attracted to the Earth (and the Earth to the Moon!) With a force directed along the straight line connecting the centers of the considered celestial bodies and equal to
where m 1 , m 2 are the masses, respectively, of the Moon and the Earth; G = 6.67e-11 m 3 / (kg * s 2 ) - gravitational constant; r 1,2- the distance between the centers of the moon and the earth. If we take into account only this force, then, having solved the problem of the motion of the Moon as a satellite of the Earth and having learned to calculate the position of the Moon in the sky against the background of stars, we will soon be convinced by direct measurements of the equatorial coordinates of the Moon that in our conservatory not everything is as smooth as I would like to. And the point here is not in the law of universal perception (and in the early stages of the development of celestial mechanics such thoughts were expressed quite often), but in unaccounted perturbation of the motion of the moon by other bodies. What kind? We look at the sky and our gaze immediately rests on a hefty, weighing as much as 1.99e30 kilograms plasma ball right under our nose - the Sun. Is the moon attracted to the sun? More like, with a force equal in magnitude
where m 3 is the mass of the Sun; r 1,3 is the distance from the moon to the sun. Compare this force with the previous one.
Take the position of the bodies, in which the attraction of the Moon to the Sun will be minimal: all three bodies are on one straight line and the Earth is located between the Moon and the Sun. In this case, our formula will look like:
Where
Here is the number! It turns out that the Moon is attracted to the Sun by a force that is more than two times greater than the force of its attraction to the Earth.
Such a disturbance can no longer be ignored, and it will definitely affect the final trajectory of the Moon. Let us go further, taking into account the assumption that the Earth’s orbit is circular with radius a, we find the locus of points around the Earth, where the force of attraction of any object to the Earth is equal to the force of its attraction to the Sun. This will be a sphere with a radius
displaced along a straight line connecting the Earth and the Sun in the opposite direction to the Sun at a distance
Where
The known orbit of the moon lies outside this area. That is, at any point of the trajectory, the Moon suffers from the Sun significantly more attraction than from the Earth.
2. Satellite or planet? Gravitational scope
This information often gives rise to disputes that the Moon is not a satellite of the Earth, but an independent planet of the Solar System, whose orbit is outraged by the attraction of the near Earth.
Let us estimate the perturbation introduced by the Sun into the trajectory of the Moon relative to the Earth, as well as the disturbance introduced by the Earth into the trajectory of the Moon relative to the Sun, using the criterion proposed by P. Laplace. Consider three bodies: the Sun (S), the Earth (E) and the Moon (M).
Let us assume that the orbits of the Earth relative to the Sun and the Moon relative to the Earth are circular.

Consider the motion of the moon in a geocentric inertial frame of reference. The absolute acceleration of the moon in the heliocentric reference system is determined by the forces acting on it and is equal to:
On the other hand, according to the Coriolis theorem, the absolute acceleration of the moon
Where
A portion of this acceleration equal to
the acceleration of the moon caused by disturbance from the sun.
If we consider the motion of the moon in the heliocentric inertial reference frame, then everything is much simpler, the acceleration
With the parameters of the orbits of the Earth and the Moon existing in the current epoch, the inequality is true at each point of the trajectory of the Moon
which can be verified by direct calculation, but I refer to the source in order not to overly clutter the article.
What does inequality (1) mean? Yes, the fact that in relative terms the effect of the perturbation of the Moon by the Sun (and very significantly) is less than the effect of the attraction of the Moon to the Earth. And vice versa, the Earth's perturbation of the geoliocentric trajectory of the Moon has a decisive influence on the nature of its movement. The influence of the earth's gravity in this case is more significant, which means the moon "belongs" to the earth by right and is its satellite.
Another interesting thing is that by turning inequality (1) into an equation, you can find the locus of points where the effects of perturbations of the Moon (and any other body) by the Earth and the Sun are the same. Unfortunately, this is not so easy as in the case of the realm of the sphere. Calculations show that this surface is described by an equation of crazy order, but close to an ellipsoid of revolution. All that we can do without unnecessary problems is to assess the overall dimensions of this surface relative to the center of the Earth. Numerically solving the equation
relative to the distance from the center of the Earth to the desired surface on a sufficient number of points, we obtain the cross section of the desired surface by the ecliptic plane

For clarity, the geocentric orbit of the moon is shown here, and the sphere we found above is relative to the sun. It can be seen from the figure that the sphere of influence, or the sphere of the gravitational action of the Earth relative to the Sun, is the surface of rotation about the X axis, flattened along the straight line connecting the Earth and the Sun (along the axis of eclipses). The moon's orbit is deep inside this imaginary surface.
For practical calculations, this surface is conveniently approximated by a sphere with a center in the center of the Earth and a radius equal to
where m is the mass of a smaller celestial body; M is the mass of the larger body, in the field of which the smaller body moves; a - the distance between the centers of bodies. In our case
This unfinished million kilometers is the theoretical limit beyond which the power of the old woman of the Earth does not extend - its influence on the trajectories of astronomical objects is so small that it can be neglected. So, to launch the Moon in a circular orbit at a distance of 38.4 million kilometers from the Earth (as some linguists do) does not work, it is physically impossible.
This sphere, for comparison, is shown in the figure by a blue dashed line. At estimated calculations, it is considered that the body inside this sphere will experience only from the side of the Earth. If the body is outside this sphere, we believe that the body moves in the field of the sun. In practical cosmonautics, a method of conjugation of conic sections is known, which makes it possible to approximately calculate the trajectory of a spacecraft using the solution of the two-body problem. In this case, all the space that the apparatus overcomes is divided into similar spheres of influence.
For example, it is now clear that in order to have a theoretical opportunity to perform maneuvers for entering a circumlunar orbit, the spacecraft must fall within the sphere of the Moon’s action relative to the Earth. Its radius is easy to calculate by the formula (3) and it is equal to 66 thousand kilometers.
Thus, the moon can rightly be considered a satellite of the Earth. However, due to the significant influence of the gravitational field of the Sun, it does not move in the central gravitational field, which means its trajectory is not a conic section.
3. The three-body problem in the classical formulation
So, we will consider a model problem in a general formulation, known in celestial mechanics as a three-body problem. Consider three bodies of arbitrary mass, arranged arbitrarily in space and moving exclusively under the action of forces of mutual gravitational attraction

The bodies are considered material points. The position of the bodies will be counted in an arbitrary basis, which is associated with the inertial reference system Oxyz . The position of each of the bodies is given by the radius vector, respectively
We write the differential equations of motion of each point in vector form.
or, taking into account (4)
In accordance with the law of the world, the interaction forces are directed along the vectors
Along each of these vectors we will release the corresponding ort
then each of the gravitational forces is calculated by the formula
Given all this, the system of equations of motion takes the form
We introduce the notation adopted in celestial mechanics.
- gravitational parameter of the attracting center. Then the equations of motion will take the final vector view.
4. Rationing of equations to dimensionless variables
A fairly popular technique in mathematical modeling is to reduce differential equations and other relations describing the process to dimensionless phase coordinates and dimensionless time. Other parameters are also normalized. This allows us to consider, albeit with the use of numerical modeling, but in a fairly general form a whole class of typical tasks. I leave the question of how justified this is in each solvable problem, but I agree that in this case, this approach is quite fair.
So, we introduce some abstract celestial body with a gravitational parameter
We introduce the replacement of parameters. For the position of the points of our system
Where
for gravity body parameters
Where
for time
Where
Now recalculate the acceleration points of the system through these dimensionless parameters. Let's apply direct double differentiation in time. For speeds
For acceleration
When substituting the obtained relations into the equations of motion, everything elegantly collapses into beautiful equations:
This system of equations is still considered non-integrable in analytic functions. Why is it considered and is not? Because the successes of the theory of the function of a complex variable led to the fact that the general solution of the three-body problem did appear in 1912 — Karl Sundman found an algorithm for finding coefficients for infinite series with respect to a complex parameter, which theoretically is a general solution of the three-body problem. But ... for the application of Zundman's series in practical calculations with the accuracy required for them, it requires obtaining such a number of members of these series that this task is much greater than the capabilities of computers even today.
Therefore, numerical integration is the only way to analyze the solution of equation (5)
5. Calculation of the initial conditions: extract the source data
As I wrote earlier , before starting the numerical integration, you should take care to calculate the initial conditions for the problem to be solved. In the problem under consideration, the search for initial conditions turns into an independent subtask, since system (5) gives us nine second-order scalar equations, which, when going to normal form, Cauchy increases the order of the system by another 2 times. That is, we need to calculate as many as 18 parameters — the initial positions and components of the initial velocity of all points of the system. Where do we get data on the position of the celestial bodies of interest to us? We live in a world where man walked on the moon - naturally, humanity must have information about how this moon moves and where it is located.
That is, you say, you, dude, offer us to take thick astronomical reference books from the shelves, blow dust from them ... They didn’t guess! I propose to go for these data to those who actually walked on the moon, to NASA, namely in the Jet Propulsion Laboratory, Pasadena, California. Here is the JPL Horizonts web interface .
Here, having spent some time studying the interface, we will get all the data we need. Choose a date, for example, yes we do not care, but let it be July 27, 2018 UT 20:21. Just at that moment there was a complete phase of the lunar eclipse. The program will give us a huge footwoman
Full output for the ephemeris of the Moon on 07/27/2018 20:21 (origin of coordinates in the center of the Earth)
*******************************************************************************
Revised: Jul 31, 2013 Moon / (Earth) 301
GEOPHYSICAL DATA (updated 2018-Aug-13):
Vol. Mean Radius, km = 1737.53+-0.03 Mass, x10^22 kg = 7.349
Radius (gravity), km = 1738.0 Surface emissivity = 0.92
Radius (IAU), km = 1737.4 GM, km^3/s^2 = 4902.800066
Density, g/cm^3 = 3.3437 GM 1-sigma, km^3/s^2 = +-0.0001
V(1,0) = +0.21 Surface accel., m/s^2 = 1.62
Earth/Moon mass ratio = 81.3005690769 Farside crust. thick. = ~80 - 90 km
Mean crustal density = 2.97+-.07 g/cm^3 Nearside crust. thick.= 58+-8 km
Heat flow, Apollo 15 = 3.1+-.6 mW/m^2 k2 = 0.024059
Heat flow, Apollo 17 = 2.2+-.5 mW/m^2 Rot. Rate, rad/s = 0.0000026617
Geometric Albedo = 0.12
Mean angular diameter = 31'05.2" Orbit period = 27.321582 d
Obliquity to orbit = 6.67 deg Eccentricity = 0.05490
Semi-major axis, a = 384400 km Inclination = 5.145 deg
Mean motion, rad/s = 2.6616995x10^-6 Nodal period = 6798.38 d
Apsidal period = 3231.50 d Mom. of inertia C/MR^2= 0.393142
beta (C-A/B), x10^-4 = 6.310213 gamma (B-A/C), x10^-4 = 2.277317
Perihelion Aphelion Mean
Solar Constant (W/m^2) 1414+-7 1323+-7 1368+-7
Maximum Planetary IR (W/m^2) 1314 1226 1268
Minimum Planetary IR (W/m^2) 5.2 5.2 5.2
*******************************************************************************
*******************************************************************************
Ephemeris / WWW_USER Wed Aug 15 20:45:05 2018 Pasadena, USA / Horizons
*******************************************************************************
Target body name: Moon (301) {source: DE431mx}
Center body name: Earth (399) {source: DE431mx}
Center-site name: BODY CENTER
*******************************************************************************
Start time : A.D. 2018-Jul-27 20:21:00.0003 TDB
Stop time : A.D. 2018-Jul-28 20:21:00.0003 TDB
Step-size : 0 steps
*******************************************************************************
Center geodetic : 0.00000000,0.00000000,0.0000000 {E-lon(deg),Lat(deg),Alt(km)}
Center cylindric: 0.00000000,0.00000000,0.0000000 {E-lon(deg),Dxy(km),Dz(km)}
Center radii : 6378.1 x 6378.1 x 6356.8 km {Equator, meridian, pole}
Output units : AU-D
Output type : GEOMETRIC cartesian states
Output format : 3 (position, velocity, LT, range, range-rate)
Reference frame : ICRF/J2000.0
Coordinate systm: Ecliptic and Mean Equinox of Reference Epoch
*******************************************************************************
JDTDB
X Y Z
VX VY VZ
LT RG RR
*******************************************************************************
$$SOE
2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB
X = 1.537109094089627E-03 Y =-2.237488447258137E-03 Z = 5.112037386426180E-06
VX= 4.593816208618667E-04 VY= 3.187527302531735E-04 VZ=-5.183707711777675E-05
LT= 1.567825598846416E-05 RG= 2.714605874095336E-03 RR=-2.707898607099066E-06
$$EOE
*******************************************************************************
Coordinate system description:
Ecliptic and Mean Equinox of Reference Epoch
Reference epoch: J2000.0 XY-plane: plane of the Earth's orbit at the reference epoch Note: obliquity of 84381.448 arcseconds wrt ICRF equator (IAU76) X-axis : out along ascending node of instantaneous plane of the Earth's orbit and the Earth's mean equator at the reference epoch Z-axis : perpendicular to the xy-plane in the directional (+ or -) sense of Earth's north pole at the reference epoch.
Symbol meaning [1 au= 149597870.700 km, 1 day= 86400.0 s]:
JDTDB Julian Day Number, Barycentric Dynamical Time X X-component of position vector (au) Y Y-component of position vector (au) Z Z-component of position vector (au) VX X-component of velocity vector (au/day) VY Y-component of velocity vector (au/day) VZ Z-component of velocity vector (au/day) LT One-way down-leg Newtonian light-time (day) RG Range; distance from coordinate center (au) RR Range-rate; radial velocity wrt coord. center (au/day)
Geometric states/elements have no aberrations applied.
Computations by ...
Solar System Dynamics Group, Horizons On-Line Ephemeris System 4800 Oak Grove Drive, Jet Propulsion Laboratory Pasadena, CA 91109 USA Information: http://ssd.jpl.nasa.gov/ Connect : telnet://ssd.jpl.nasa.gov:6775 (via browser) http://ssd.jpl.nasa.gov/?horizons telnet ssd.jpl.nasa.gov 6775 (via command-line) Author : Jon.D.Giorgini@jpl.nasa.gov*******************************************************************************
Br-rr, what is it? Without panic, for someone who taught astronomy well at school, there is nothing to fear for mechanics and mathematics. So, the most important final search coordinates and components of the velocity of the moon.
$$SOE
2458327.347916670 = A.D. 2018-Jul-2720:21:00.0003 TDB
X = 1.537109094089627E-03 Y =-2.237488447258137E-03 Z = 5.112037386426180E-06
VX= 4.593816208618667E-04 VY= 3.187527302531735E-04 VZ=-5.183707711777675E-05
LT= 1.567825598846416E-05 RG= 2.714605874095336E-03 RR=-2.707898607099066E-06
$$EOE
Yes, yes, yes, they are Cartesian! If you carefully read the entire footcloth, then we learn that the origin of this coordinate system coincides with the center of the Earth. The XY plane lies in the plane of the earth's orbit (the plane of the ecliptic) for the epoch J2000. The X axis is directed along the line of intersection of the equatorial plane of the Earth and the ecliptic to the vernal equinox. The Z axis looks in the direction of the north pole of the Earth perpendicular to the plane of the ecliptic. Well, the Y axis complements all this happiness to the right three vectors. By default, the units of measurement of coordinates are astronomical units (the clever ones from NASA also give the value of the autronomic unit in kilometers). Speed units: astronomical units per day, day is assumed to be 86400 seconds. Full stuffing!
Similar information can be obtained for the Earth.
Full output of the Earth's ephemeris on 07/27/2018 20:21 (the origin of coordinates in the center of mass of the Solar system)
*******************************************************************************
Revised: Jul 31, 2013 Earth 399
GEOPHYSICAL PROPERTIES (revised Aug 13, 2018):
Vol. Mean Radius (km) = 6371.01+-0.02 Mass x10^24 (kg)= 5.97219+-0.0006
Equ. radius, km = 6378.137 Mass layers:
Polar axis, km = 6356.752 Atmos = 5.1 x 10^18 kg
Flattening = 1/298.257223563 oceans = 1.4 x 10^21 kg
Density, g/cm^3 = 5.51 crust = 2.6 x 10^22 kg
J2 (IERS 2010) = 0.00108262545 mantle = 4.043 x 10^24 kg
g_p, m/s^2 (polar) = 9.8321863685 outer core = 1.835 x 10^24 kg
g_e, m/s^2 (equatorial) = 9.7803267715 inner core = 9.675 x 10^22 kg
g_o, m/s^2 = 9.82022 Fluid core rad = 3480 km
GM, km^3/s^2 = 398600.435436 Inner core rad = 1215 km
GM 1-sigma, km^3/s^2 = 0.0014 Escape velocity = 11.186 km/s
Rot. Rate (rad/s) = 0.00007292115 Surface Area:
Mean sidereal day, hr = 23.9344695944 land = 1.48 x 10^8 km
Mean solar day 2000.0, s = 86400.002 sea = 3.62 x 10^8 km
Mean solar day 1820.0, s = 86400.0
Moment of inertia = 0.3308 Love no., k2 = 0.299
Mean Temperature, K = 270 Atm. pressure = 1.0 bar
Vis. mag. V(1,0) = -3.86 Volume, km^3 = 1.08321 x 10^12
Geometric Albedo = 0.367 Magnetic moment = 0.61 gauss Rp^3
Solar Constant (W/m^2) = 1367.6 (mean), 1414 (perihelion), 1322 (aphelion)
ORBIT CHARACTERISTICS:
Obliquity to orbit, deg = 23.4392911 Sidereal orb period = 1.0000174 y
Orbital speed, km/s = 29.79 Sidereal orb period = 365.25636 d
Mean daily motion, deg/d = 0.9856474 Hill's sphere radius = 234.9
*******************************************************************************
*******************************************************************************
Ephemeris / WWW_USER Wed Aug 15 21:16:21 2018 Pasadena, USA / Horizons
*******************************************************************************
Target body name: Earth (399) {source: DE431mx}
Center body name: Solar System Barycenter (0) {source: DE431mx}
Center-site name: BODY CENTER
*******************************************************************************
Start time : A.D. 2018-Jul-27 20:21:00.0003 TDB
Stop time : A.D. 2018-Jul-28 20:21:00.0003 TDB
Step-size : 0 steps
*******************************************************************************
Center geodetic : 0.00000000,0.00000000,0.0000000 {E-lon(deg),Lat(deg),Alt(km)}
Center cylindric: 0.00000000,0.00000000,0.0000000 {E-lon(deg),Dxy(km),Dz(km)}
Center radii : (undefined)
Output units : AU-D
Output type : GEOMETRIC cartesian states
Output format : 3 (position, velocity, LT, range, range-rate)
Reference frame : ICRF/J2000.0
Coordinate systm: Ecliptic and Mean Equinox of Reference Epoch
*******************************************************************************
JDTDB
X Y Z
VX VY VZ
LT RG RR
*******************************************************************************
$$SOE
2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB
X = 5.755663665315949E-01 Y =-8.298818915224488E-01 Z =-5.366994499016168E-05
VX= 1.388633512282171E-02 VY= 9.678934168415631E-03 VZ= 3.429889230737491E-07
LT= 5.832932117417083E-03 RG= 1.009940888883960E+00 RR=-3.947237246302148E-05
$$EOE
*******************************************************************************
Coordinate system description:
Ecliptic and Mean Equinox of Reference Epoch
Reference epoch: J2000.0 XY-plane: plane of the Earth's orbit at the reference epoch Note: obliquity of 84381.448 arcseconds wrt ICRF equator (IAU76) X-axis : out along ascending node of instantaneous plane of the Earth's orbit and the Earth's mean equator at the reference epoch Z-axis : perpendicular to the xy-plane in the directional (+ or -) sense of Earth's north pole at the reference epoch.
Symbol meaning [1 au= 149597870.700 km, 1 day= 86400.0 s]:
JDTDB Julian Day Number, Barycentric Dynamical Time X X-component of position vector (au) Y Y-component of position vector (au) Z Z-component of position vector (au) VX X-component of velocity vector (au/day) VY Y-component of velocity vector (au/day) VZ Z-component of velocity vector (au/day) LT One-way down-leg Newtonian light-time (day) RG Range; distance from coordinate center (au) RR Range-rate; radial velocity wrt coord. center (au/day)
Geometric states/elements have no aberrations applied.
Computations by ...
Solar System Dynamics Group, Horizons On-Line Ephemeris System 4800 Oak Grove Drive, Jet Propulsion Laboratory Pasadena, CA 91109 USA Information: http://ssd.jpl.nasa.gov/ Connect : telnet://ssd.jpl.nasa.gov:6775 (via browser) http://ssd.jpl.nasa.gov/?horizons telnet ssd.jpl.nasa.gov 6775 (via command-line) Author : Jon.D.Giorgini@jpl.nasa.gov*******************************************************************************
Here, the barycenter (center of mass) of the Solar system is chosen as the origin of coordinates. The data we are interested in
$$SOE
2458327.347916670 = A.D. 2018-Jul-2720:21:00.0003 TDB
X = 5.755663665315949E-01 Y =-8.298818915224488E-01 Z =-5.366994499016168E-05
VX= 1.388633512282171E-02 VY= 9.678934168415631E-03 VZ= 3.429889230737491E-07
LT= 5.832932117417083E-03 RG= 1.009940888883960E+00 RR=-3.947237246302148E-05
$$EOE
For the moon, we will need the coordinates and speed relative to the barycenter of the solar system, we can calculate them, or we can ask NASA to give us such data
Full output of the Moon's ephemeris on 07/27/2018 20:21 (the origin of coordinates in the center of mass of the Solar System)
*******************************************************************************
Revised: Jul 31, 2013 Moon / (Earth) 301
GEOPHYSICAL DATA (updated 2018-Aug-13):
Vol. Mean Radius, km = 1737.53+-0.03 Mass, x10^22 kg = 7.349
Radius (gravity), km = 1738.0 Surface emissivity = 0.92
Radius (IAU), km = 1737.4 GM, km^3/s^2 = 4902.800066
Density, g/cm^3 = 3.3437 GM 1-sigma, km^3/s^2 = +-0.0001
V(1,0) = +0.21 Surface accel., m/s^2 = 1.62
Earth/Moon mass ratio = 81.3005690769 Farside crust. thick. = ~80 - 90 km
Mean crustal density = 2.97+-.07 g/cm^3 Nearside crust. thick.= 58+-8 km
Heat flow, Apollo 15 = 3.1+-.6 mW/m^2 k2 = 0.024059
Heat flow, Apollo 17 = 2.2+-.5 mW/m^2 Rot. Rate, rad/s = 0.0000026617
Geometric Albedo = 0.12
Mean angular diameter = 31'05.2" Orbit period = 27.321582 d
Obliquity to orbit = 6.67 deg Eccentricity = 0.05490
Semi-major axis, a = 384400 km Inclination = 5.145 deg
Mean motion, rad/s = 2.6616995x10^-6 Nodal period = 6798.38 d
Apsidal period = 3231.50 d Mom. of inertia C/MR^2= 0.393142
beta (C-A/B), x10^-4 = 6.310213 gamma (B-A/C), x10^-4 = 2.277317
Perihelion Aphelion Mean
Solar Constant (W/m^2) 1414+-7 1323+-7 1368+-7
Maximum Planetary IR (W/m^2) 1314 1226 1268
Minimum Planetary IR (W/m^2) 5.2 5.2 5.2
*******************************************************************************
*******************************************************************************
Ephemeris / WWW_USER Wed Aug 15 21:19:24 2018 Pasadena, USA / Horizons
*******************************************************************************
Target body name: Moon (301) {source: DE431mx}
Center body name: Solar System Barycenter (0) {source: DE431mx}
Center-site name: BODY CENTER
*******************************************************************************
Start time : A.D. 2018-Jul-27 20:21:00.0003 TDB
Stop time : A.D. 2018-Jul-28 20:21:00.0003 TDB
Step-size : 0 steps
*******************************************************************************
Center geodetic : 0.00000000,0.00000000,0.0000000 {E-lon(deg),Lat(deg),Alt(km)}
Center cylindric: 0.00000000,0.00000000,0.0000000 {E-lon(deg),Dxy(km),Dz(km)}
Center radii : (undefined)
Output units : AU-D
Output type : GEOMETRIC cartesian states
Output format : 3 (position, velocity, LT, range, range-rate)
Reference frame : ICRF/J2000.0
Coordinate systm: Ecliptic and Mean Equinox of Reference Epoch
*******************************************************************************
JDTDB
X Y Z
VX VY VZ
LT RG RR
*******************************************************************************
$$SOE
2458327.347916670 = A.D. 2018-Jul-27 20:21:00.0003 TDB
X = 5.771034756256845E-01 Y =-8.321193799697072E-01 Z =-4.855790760378579E-05
VX= 1.434571674368357E-02 VY= 9.997686898668805E-03 VZ=-5.149408819470315E-05
LT= 5.848610189172283E-03 RG= 1.012655462859054E+00 RR=-3.979984423450087E-05
$$EOE
*******************************************************************************
Coordinate system description:
Ecliptic and Mean Equinox of Reference Epoch
Reference epoch: J2000.0 XY-plane: plane of the Earth's orbit at the reference epoch Note: obliquity of 84381.448 arcseconds wrt ICRF equator (IAU76) X-axis : out along ascending node of instantaneous plane of the Earth's orbit and the Earth's mean equator at the reference epoch Z-axis : perpendicular to the xy-plane in the directional (+ or -) sense of Earth's north pole at the reference epoch.
Symbol meaning [1 au= 149597870.700 km, 1 day= 86400.0 s]:
JDTDB Julian Day Number, Barycentric Dynamical Time X X-component of position vector (au) Y Y-component of position vector (au) Z Z-component of position vector (au) VX X-component of velocity vector (au/day) VY Y-component of velocity vector (au/day) VZ Z-component of velocity vector (au/day) LT One-way down-leg Newtonian light-time (day) RG Range; distance from coordinate center (au) RR Range-rate; radial velocity wrt coord. center (au/day)
Geometric states/elements have no aberrations applied.
Computations by ...
Solar System Dynamics Group, Horizons On-Line Ephemeris System 4800 Oak Grove Drive, Jet Propulsion Laboratory Pasadena, CA 91109 USA Information: http://ssd.jpl.nasa.gov/ Connect : telnet://ssd.jpl.nasa.gov:6775 (via browser) http://ssd.jpl.nasa.gov/?horizons telnet ssd.jpl.nasa.gov 6775 (via command-line) Author : Jon.D.Giorgini@jpl.nasa.gov*******************************************************************************
$$SOE
2458327.347916670 = A.D. 2018-Jul-2720:21:00.0003 TDB
X = 5.771034756256845E-01 Y =-8.321193799697072E-01 Z =-4.855790760378579E-05
VX= 1.434571674368357E-02 VY= 9.997686898668805E-03 VZ=-5.149408819470315E-05
LT= 5.848610189172283E-03 RG= 1.012655462859054E+00 RR=-3.979984423450087E-05
$$EOE
Wonderful! Now it is necessary to slightly process the received data with a file.
6. 38 parrots and one parrot wing
To begin with, we will define the scale, because our equations of motion (5) are written in dimensionless form. The data provided by NASA themselves tell us that for the scale of the coordinates is to take one astronomical unit. Accordingly, as a reference body, to which we will ration the masses of other bodies, we take the Sun, and as the time scale, the period of the Earth’s orbit around the Sun.
All this is of course very good, but we did not set the initial conditions for the sun. “Why?” Some linguist would ask me. And I would say that the Sun is not motionless at all, but also rotates in its orbit around the center of mass of the Solar system. This can be seen by looking at the NASA data for the sun.
$$SOE
2458327.347916670 = A.D. 2018-Jul-2720:21:00.0003 TDB
X = 6.520050993518213E+04 Y = 1.049687363172734E+06 Z =-1.304404963058507E+04
VX=-1.265326939350981E-02 VY= 5.853475278436883E-03 VZ= 3.136673455633667E-04
LT= 3.508397935601254E+00 RG= 1.051791240756026E+06 RR= 5.053500842402456E-03
$$EOE
Looking at the RG parameter, we will see that the Sun rotates around the solar system barycenter, and on 07/27/2018, the center of the star is at a distance of one million kilometers. The radius of the sun, for reference - 696 thousand kilometers. That is, the barycenter of the solar system lies half a million kilometers from the surface of the star. Why? Yes, because all other bodies interacting with the Sun also inform him of the acceleration, mainly, of course, the heavy Jupiter. Accordingly, the Sun also has its own orbit.
Of course, we can choose these data as initial conditions, but no - we solve the three-body model problem, and Jupiter and other characters are not included in it. So to the detriment of realism, knowing the position and velocity of the Earth and the Moon, we recalculate the initial conditions for the Sun, so that the center of mass of the Sun-Earth-Moon system is at the origin. For the center of mass of our mechanical system, the equation
We place the center of mass at the origin, that is, let us set
from where
We turn to the dimensionless coordinates and parameters by selecting
Differentiating (6) over time and moving to dimensionless time, we also obtain the ratio for the velocities
Where
Now we will write a program that will form the initial conditions in the “parrots” we have chosen. What will we write on? Of course on Python! After all, as you know, this is the best language for mathematical modeling.
However, if we get away from sarcasm, then we will really try a python for this purpose, and why not? I will definitely provide a link to all the code in my Github profile .
Calculation of the initial conditions for the system Moon - Earth - Sun
## Исходные данные задачи## Гравитационная постоянная
G = 6.67e-11# Массы тел (Луна, Земля, Солнце)
m = [7.349e22, 5.792e24, 1.989e30]
# Расчитываем гравитационные параметры тел
mu = []
print("Гравитационные параметры тел")
for i, mass in enumerate(m):
mu.append(G * mass)
print("mu[" + str(i) + "] = " + str(mu[i]))
# Нормируем гравитационные параметры к Солнцу
kappa = []
print("Нормированные гравитационные параметры")
for i, gp in enumerate(mu):
kappa.append(gp / mu[2])
print("xi[" + str(i) + "] = " + str(kappa[i]))
print("\n")
# Астрономическая единица
a = 1.495978707e11import math
# Масштаб безразмерного времени, c
T = 2 * math.pi * a * math.sqrt(a / mu[2])
print("Масштаб времени T = " + str(T) + "\n")
# Координаты NASA для Луны
xL = 5.771034756256845E-01
yL = -8.321193799697072E-01
zL = -4.855790760378579E-05import numpy as np
xi_10 = np.array([xL, yL, zL])
print("Начальное положение Луны, а.е.: " + str(xi_10))
# Координаты NASA для Земли
xE = 5.755663665315949E-01
yE = -8.298818915224488E-01
zE = -5.366994499016168E-05
xi_20 = np.array([xE, yE, zE])
print("Начальное положение Земли, а.е.: " + str(xi_20))
# Расчитываем начальное положение Солнца, полагая что начало координат - в центре масс всей системы
xi_30 = - kappa[0] * xi_10 - kappa[1] * xi_20
print("Начальное положение Солнца, а.е.: " + str(xi_30))
# Вводим константы для вычисления безразмерных скоростей
Td = 86400.0
u = math.sqrt(mu[2] / a) / 2 / math.pi
print("\n")
# Начальная скорость Луны
vxL = 1.434571674368357E-02
vyL = 9.997686898668805E-03
vzL = -5.149408819470315E-05
vL0 = np.array([vxL, vyL, vzL])
uL0 = np.array([0.0, 0.0, 0.0])
for i, v in enumerate(vL0):
vL0[i] = v * a / Td
uL0[i] = vL0[i] / u
print("Начальная скорость Луны, м/с: " + str(vL0))
print(" -//- безразмерная: " + str(uL0))
# Начальная скорость Земли
vxE = 1.388633512282171E-02
vyE = 9.678934168415631E-03
vzE = 3.429889230737491E-07
vE0 = np.array([vxE, vyE, vzE])
uE0 = np.array([0.0, 0.0, 0.0])
for i, v in enumerate(vE0):
vE0[i] = v * a / Td
uE0[i] = vE0[i] / u
print("Начальная скорость Земли, м/с: " + str(vE0))
print(" -//- безразмерная: " + str(uE0))
# Начальная скорость Солнца
vS0 = - kappa[0] * vL0 - kappa[1] * vE0
uS0 = - kappa[0] * uL0 - kappa[1] * uE0
print("Начальная скорость Солнца, м/с: " + str(vS0))
print(" -//- безразмерная: " + str(uS0))
Program exhaust
Гравитационные параметры тел
mu[0] = 4901783000000.0
mu[1] = 386326400000000.0
mu[2] = 1.326663e+20
Нормированные гравитационные параметры
xi[0] = 3.6948215183509304e-08
xi[1] = 2.912016088486677e-06
xi[2] = 1.0
Масштаб времени T = 31563683.35432583
Начальное положение Луны, а.е.: [ 5.77103476e-01-8.32119380e-01-4.85579076e-05]
Начальное положение Земли, а.е.: [ 5.75566367e-01-8.29881892e-01-5.36699450e-05]
Начальное положение Солнца, а.е.: [-1.69738146e-062.44737475e-061.58081871e-10]
Начальная скорость Луны, м/с: [24838.9893347317310.56333294-89.15979106]
-//- безразмерная: [ 5.24078311 3.65235907 -0.01881184]
Начальная скорость Земли, м/с: [2.40435899e+041.67586567e+045.93870516e-01]
-//- безразмерная: [5.07296163e+00 3.53591219e+00 1.25300854e-04]
Начальная скорость Солнца, м/с: [-7.09330769e-02-4.94410725e-021.56493465e-06]
-//- безразмерная: [-1.49661835e-05 -1.04315813e-05 3.30185861e-10]7. Integrating the equations of motion and analyzing the results
Actually, the integration itself boils down to a more or less standard for SciPy procedure for preparing a system of equations: transforming an ODE system to the Cauchy form and calling the corresponding solver functions. To transform the system into a Cauchy form, we recall that
Then by entering the system state vector
we reduce (7) and (5) to one vector equation
To integrate (8) with the initial conditions, we write a little, quite a bit of code
Integrating the equations of motion in the three-body problem
## Вычисление векторов обобщенных ускорений#defcalcAccels(xi):
k = 4 * math.pi ** 2
xi12 = xi[1] - xi[0]
xi13 = xi[2] - xi[0]
xi23 = xi[2] - xi[1]
s12 = math.sqrt(np.dot(xi12, xi12))
s13 = math.sqrt(np.dot(xi13, xi13))
s23 = math.sqrt(np.dot(xi23, xi23))
a1 = (k * kappa[1] / s12 ** 3) * xi12 + (k * kappa[2] / s13 ** 3) * xi13
a2 = -(k * kappa[0] / s12 ** 3) * xi12 + (k * kappa[2] / s23 ** 3) * xi23
a3 = -(k * kappa[0] / s13 ** 3) * xi13 - (k * kappa[1] / s23 ** 3) * xi23
return [a1, a2, a3]
## Система уравнений в нормальной форме Коши#deff(t, y):
n = 9
dydt = np.zeros((2 * n))
for i in range(0, n):
dydt[i] = y[i + n]
xi1 = np.array(y[0:3])
xi2 = np.array(y[3:6])
xi3 = np.array(y[6:9])
accels = calcAccels([xi1, xi2, xi3])
i = n
for accel in accels:
for a in accel:
dydt[i] = a
i = i + 1return dydt
# Начальные условия задачи Коши
y0 = [xi_10[0], xi_10[1], xi_10[2],
xi_20[0], xi_20[1], xi_20[2],
xi_30[0], xi_30[1], xi_30[2],
uL0[0], uL0[1], uL0[2],
uE0[0], uE0[1], uE0[2],
uS0[0], uS0[1], uS0[2]]
## Интегрируем уравнения движения## Начальное время
t_begin = 0# Конечное время
t_end = 30.7 * Td / T;
# Интересующее нас число точек траектории
N_plots = 1000# Шаг времени между точкими
step = (t_end - t_begin) / N_plots
import scipy.integrate as spi
solver = spi.ode(f)
solver.set_integrator('vode', nsteps=50000, method='bdf', max_step=1e-6, rtol=1e-12)
solver.set_initial_value(y0, t_begin)
ts = []
ys = []
i = 0while solver.successful() and solver.t <= t_end:
solver.integrate(solver.t + step)
ts.append(solver.t)
ys.append(solver.y)
print(ts[i], ys[i])
i = i + 1Let's see what we did. The result was a spatial trajectory of the moon for the first 29 days from the chosen starting point.

as well as its projection into the ecliptic plane.

“Hey, uncle, what are you giving us?” It's a circle! ”
First, it’s not a circle - there is a noticeable shift in the projection of the trajectory from the origin to the right and down. Secondly - you notice nothing? No, well, really?

I promise to prepare a rationale for that (based on the analysis of the errors of the account and NASA data) that the resulting shift in the trajectory is not due to integration errors. While I suggest the reader to take my word for it - this shift is a consequence of the solar perturbation of the lunar trajectory. Spin one more turn


In both! And pay attention to the fact that, based on the initial data of the task, the Sun is just in that direction, where the trajectory of the Moon is shifted on each turn. Yes, this insolent Sun steals our favorite companion! Oh, this is the sun!
It can be concluded that solar gravity affects the moon's orbit quite significantly - the old woman does not walk twice through the sky in the same way. A picture for six months of movement allows (at least qualitatively) to make sure of this (the picture is clickable) Interesting? Still would. Astronomy is generally entertaining science.

P.S
In the university where I studied and worked for almost seven years - the Novocherkassk Polytechnic Institute - an annual student Olympiad on the theoretical mechanics of universities in the North Caucasus was held annually. Three times we took the All-Russian Olympiad. At the opening, our main "Olympian", Professor Kondratenko AI, always said: "Academician Krylov called mechanics the poetry of the exact sciences."
I love mechanics. All the good things that I have achieved in my life and career have happened thanks to this science and my wonderful teachers. I respect the mechanics.
Therefore, I will never allow anyone to scoff at this science and brazenly exploit it for their own purposes to anyone, even if it is at least three times a PhD and a linguist four times, and has developed at least a million training programs. I sincerely believe that writing articles on a popular public resource should provide for their careful reading, normal design (LaTeX formulas are not the whim of resource developers!) And the absence of errors leading to results that violate the laws of nature. The latter is generally a “must have”.
I often tell my students: “The computer frees your hands, but this does not mean that you need to turn off the brain as well.”
I also urge you, my dear readers, to appreciate and respect the mechanics. I will gladly answer any questions, and the source code of the example of solving the three-body problem in Python, as promised,I post it on my Github profile .
Thanks for attention!
