Compressed light or What have gravitational waves
Hello GT! Today we’ll talk about one unusual state of light and its equally unusual applications. Welcome to cat.
The Heisenberg uncertainty relation forbids simultaneously measuring the coordinate and speed (momentum) of a particle. Moreover, no one bothers to accurately measure one of the quantities - but then the second uncertainty will become even greater.

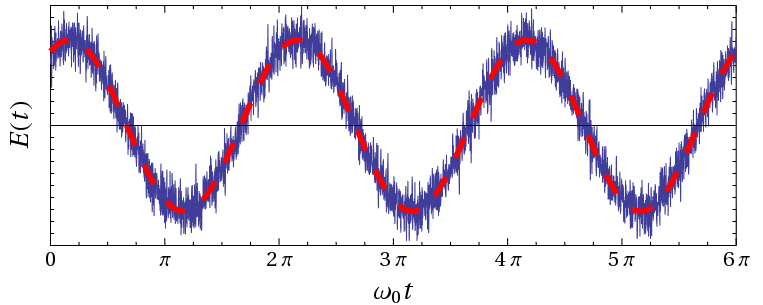
In general, uncertainty relations are quite common in physics. For example, the same relation is true for an electromagnetic wave: it relates its intensity (= number of photons) and phase :

Due to this uncertainty, we cannot accurately measure the sinusoid described by the wave, for the observer it will always be in noise haze:
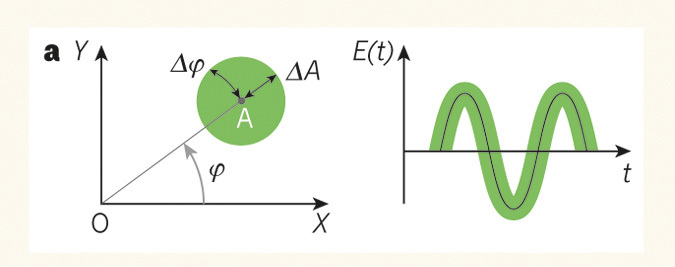
This can be clearly shown in a pie chart, where the amplitude corresponds to the radius to the point, phase - the angle between the direction of the point and the X axis. Green shows the uncertainty:
In this case, no one bothers to accurately determine either the amplitude or the phase. Then the circle of errors will turn into an ellipse, shrinking in one direction and stretching out in the other:

This condition is called squeezed light , because amplitude or phase fluctuations are compressed along one of the axes, reducing the measurement error. The first is called amplitude compression (the ellipse is stretched across the radius, you can accurately measure the amplitude at the maxima-minima of the sine wave); the second - phase (ellipse along the radius, you can measure the phase at the zeros of the sine wave).
For ordinary light, we cannot measure the amplitude or phase more accurately than the circle of errors gives us. This is called the standard quantum noise level . Compressed light allows you to reduce the error in one direction and "dive" under this noise level. In a sense, we can [pathos_mode_on] take more accurate measurements than nature would like [pathos_mode_off].
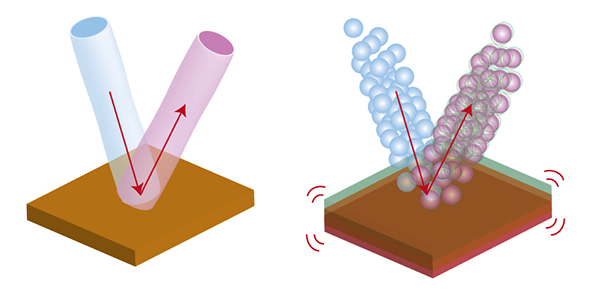
Every light source generates an integer number of photons every second. It can change from second to second due to the quantum nature of light, forming the distribution of the number of photons (I mentioned this in the story about Hanbury Brown and Twiss ).
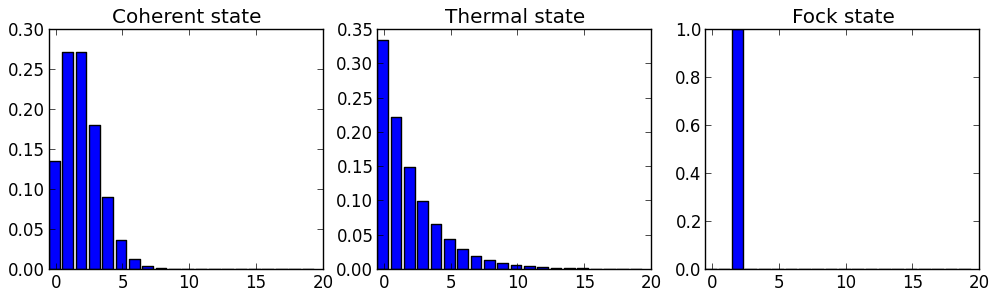
The number of photons is the same as the intensity of light. That is, the intensity is a little "noise" - varies from second to second. This is the standard quantum noise level.
But if the number of photons does not change from second to second (figure on the right), then the intensity is strictly constant and devoid of any noise. This will be the light that is maximally compressed in amplitude. The flow of photons at the same time looks something like this:

That is, photons are emitted strictly periodically. If the periodicity is violated, the light still remains to some extent compressed.
Unlike other exotic objects, the use of compressed light turned out to be very promising.
Telecom. The transmission of information by modulating a compressed variable (amplitude (AM) or phase (FM), the more general term quadrature) allows you to increase the signal-to-noise ratio. It is possible to build amplifiers that add noise only to that quadrature, which is uncompressed and does not carry a useful signal.
Quantum entanglement. In some cases, parallels can be drawn between the entanglement of photons and the compression of light. For example, you can confuse two beams of light: one squeezed in amplitude, the second in phase.
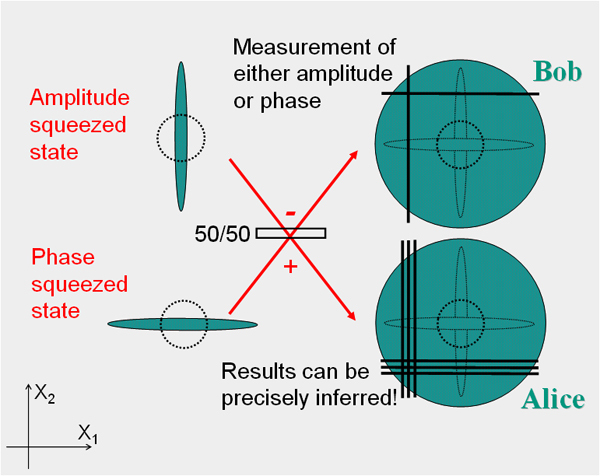
Quantum cryptography. Stems from quantum entanglement and the picture above. In the simplest quantum cryptography scheme, Alice transmits information to Bob using randomly polarized photons. The direction of compression can play the role of compression: if it is improperly selected, an attacker who intercepts the communication channel will measure noise rather than signal.
Gravitational wave detectors. For this task, you need to catch the smallest fluctuations of huge loads. This is usually done using a Michelson interferometer. It is built very simply: a laser, two mirrors and one translucent plate:
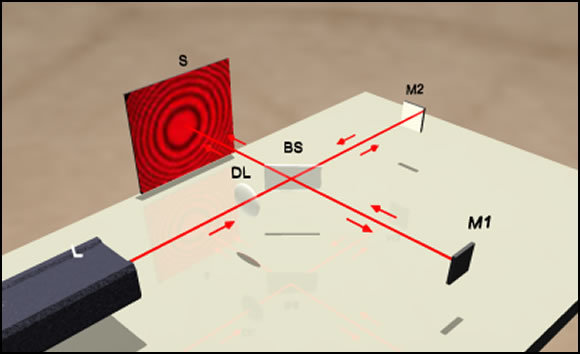
A laser is reflected from two mirrors, two reflections interfere, and an interference pattern forms on the screen. If one of the mirrors moves, then the picture also moves. This happens due to a change in the phase of the wave: the mirror has moved away - the laser path has become a little longer, an additional phase has come in - the interference strips have shifted.
Since the interferometer measures the phase, its resolution cannot be better than the phase uncertainty. For a conventional laser, it is limited to a standard quantum noise level. But if you replace the laser with a phase-squeezed light source, then this problem will disappear, and we will be able to measure distances with unprecedented accuracy.
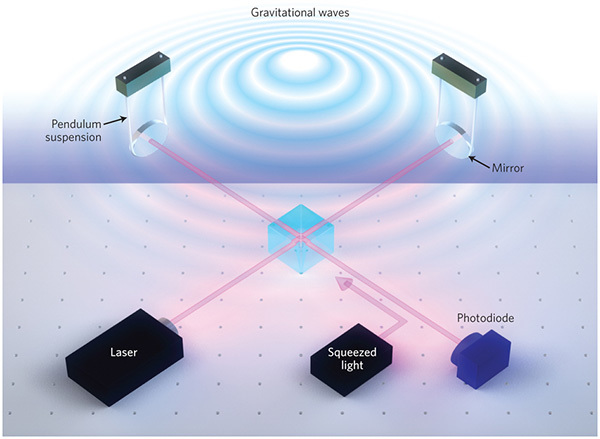
Today this is done in one of the largest gravitational wave detectors GEO600, and, apparently, is planned for the LISA space detector. By the way, among GT users there is Shkaff , who is just doing this and is ready to answer your questions in the comments.
Accurate phase measurement. Phase-squeezed light can be useful for measurements using the phase contrast method, an everyday technique in modern biology.
Creating compressed light is not so simple. For this, nonlinear optical processes are used. It’s rather difficult to explain on the fingers, but I’ll give one example.
In some crystals, an effect called Kerr nonlinearity is observed - the dependence of the refractive index on the light intensity. Let's send a laser pulse to such a crystal. For any pulse, the intensity at the fronts is lower than in the center — which means that the refractive index will change most strongly where the center of the pulse is now. The difference in refractive indices leads to the fact that the phase of the wave at the center and at the fronts varies differently. The totality of these changes leads to the fact that the phase becomes defined a little better than usual, and the intensity - on the contrary, a little worse. Hello, squeezed light :).
Compressed light can also be measured in several ways.
1. Hanbury Brown-Twiss scheme.
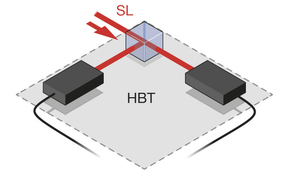
In a series about Hanbury Brown and Twiss, I said that the correlation function g (2) corresponds to the width of the distribution of the number of photons. Amplitude compression of light means that the number of photons is determined better than usual. Therefore, in the broad sense of the word g (2) is less than unity - a sign of squeezed light.
2. Balance detector. This is like the Hanbury Brown-Twiss circuit, but instead of correlations, we either subtract or add signals from two diodes (at our request):
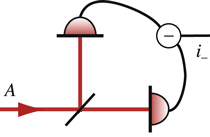
A translucent mirror transmits or reflects each photon randomly. This randomness introduces additional quantum noise (such as shot noise ) into the signal . Such noise has a different sign on two diodes: if a photon is reflected, then it will not fly by; if it flies, it will not be reflected.
If we subtract the signal from one diode from another, then the quantum noise will not go anywhere. And if we add up? Then the noise will disappear, because it has a different sign. (Another explanation: we divided the light into two parts, and then folded them back - this, obviously, did not add additional noise.)
So, subtraction adds us noise with a standard quantum level, and addition does not change anything. If the studied light was amplitude-squeezed (ie, “noiseless”), then subtraction will make it more noisy, and addition will leave it unchanged. Switching between addition and subtraction, we can measure the noise level, and if it is different, then we observe amplitude-squeezed light.
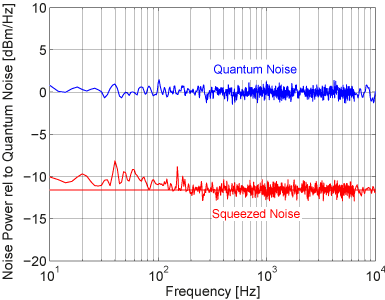
The noise after addition (red) and subtraction (blue) looks something like this. Red noise is much weaker and corresponds to compressed light.
3. Homodyination. Amplitude compression is easy to measure, but what about phase compression? If it is possible to “rotate” the orientation of the ellipse (that is, the phase of light), then the light from the phase-squeezed will become amplitude-squeezed. The phase can be rotated by mixing the light with the reference wave. This is very similar to the receiver-local oscillator, only in the local oscillator the frequency of the reference and studied waves is different, but in the local oscillator it is not (hence the name).
Even in the homodyne, you need to select the phase of the reference wave. In electronics, this is done by a phase shifter, in optics by a delay line (the later the light arrives, the more the phase will run). Mixing takes place on the same translucent mirror:
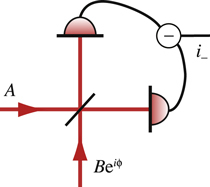
The reference wave comes from below. And then - the same balanced detector.
So far, compressed light is used only in ultra-precise interferometry. The problem is that it is incredibly fragile. This is easy to understand by the example of ideal amplitude-squeezed light (the photon flux is strictly periodic):

In the propagation of light, losses are inevitable, which are always accidental. This means that the photons will disappear from the stream at random:

As you can see, almost nothing remains of the periodicity. As well as from compression. Therefore, compressed light is very difficult to transmit over long distances.
And finally, let's admire the scheme of the gravitational detector GEO 600 near Hanover:
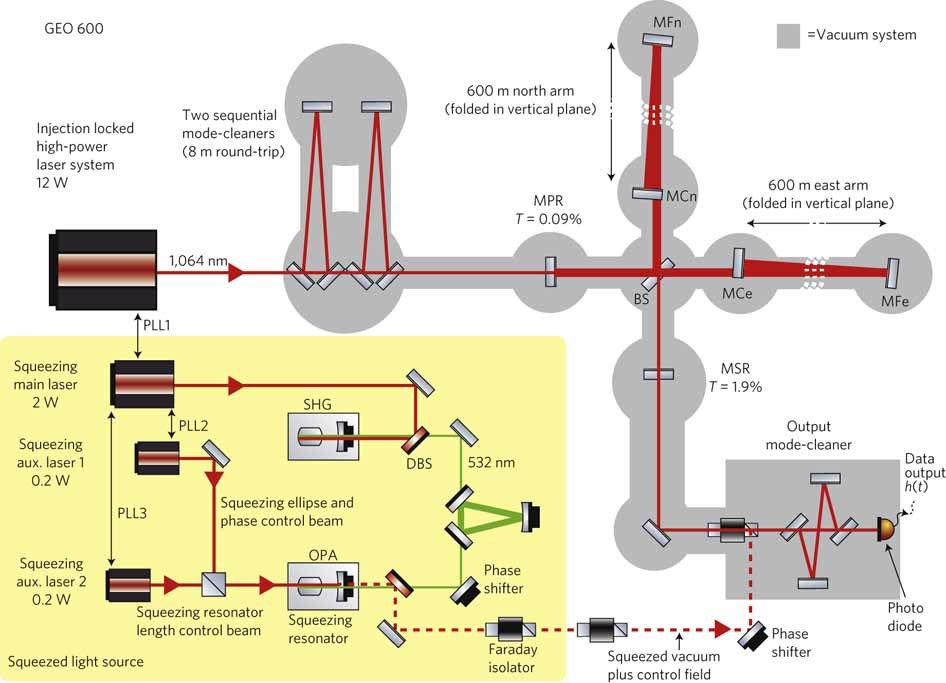
The source of compressed light is on a yellow background. It uses a nonlinear optical process, but not Kerr nonlinearity, but the generation of the second harmonic of the radiation. The red dotted line is compressed light. Above right is a Michelson interferometer with shoulders of 600 meters; mirrors are suspended on loads that must oscillate from gravitational waves. The picture from the interferometer is obtained on the photodiode in the lower right corner.
Sources of
M. Fox. Quantum optics: An Introduction - Oxford University Press, 2006.
Thanks to Shkaff for the expert comments. Free
images: KDPV , 1 , 2 , 3 , 4 , 5 ,6 , 7 , 8 , 9 , 10 .

A policeman stops Heisenberg who has exceeded speed.(bearded anecdote)
“Do you even know how fast you were driving?”
“No, but I know exactly where I was.”
The Heisenberg uncertainty relation forbids simultaneously measuring the coordinate and speed (momentum) of a particle. Moreover, no one bothers to accurately measure one of the quantities - but then the second uncertainty will become even greater.

In general, uncertainty relations are quite common in physics. For example, the same relation is true for an electromagnetic wave: it relates its intensity (= number of photons) and phase :

Due to this uncertainty, we cannot accurately measure the sinusoid described by the wave, for the observer it will always be in noise haze:

This can be clearly shown in a pie chart, where the amplitude corresponds to the radius to the point, phase - the angle between the direction of the point and the X axis. Green shows the uncertainty:

In this case, no one bothers to accurately determine either the amplitude or the phase. Then the circle of errors will turn into an ellipse, shrinking in one direction and stretching out in the other:

This condition is called squeezed light , because amplitude or phase fluctuations are compressed along one of the axes, reducing the measurement error. The first is called amplitude compression (the ellipse is stretched across the radius, you can accurately measure the amplitude at the maxima-minima of the sine wave); the second - phase (ellipse along the radius, you can measure the phase at the zeros of the sine wave).
Why is it important?
For ordinary light, we cannot measure the amplitude or phase more accurately than the circle of errors gives us. This is called the standard quantum noise level . Compressed light allows you to reduce the error in one direction and "dive" under this noise level. In a sense, we can [pathos_mode_on] take more accurate measurements than nature would like [pathos_mode_off].
A simple example.
Every light source generates an integer number of photons every second. It can change from second to second due to the quantum nature of light, forming the distribution of the number of photons (I mentioned this in the story about Hanbury Brown and Twiss ).

The number of photons is the same as the intensity of light. That is, the intensity is a little "noise" - varies from second to second. This is the standard quantum noise level.
But if the number of photons does not change from second to second (figure on the right), then the intensity is strictly constant and devoid of any noise. This will be the light that is maximally compressed in amplitude. The flow of photons at the same time looks something like this:

That is, photons are emitted strictly periodically. If the periodicity is violated, the light still remains to some extent compressed.
Why is this needed?
Unlike other exotic objects, the use of compressed light turned out to be very promising.
Telecom. The transmission of information by modulating a compressed variable (amplitude (AM) or phase (FM), the more general term quadrature) allows you to increase the signal-to-noise ratio. It is possible to build amplifiers that add noise only to that quadrature, which is uncompressed and does not carry a useful signal.
Quantum entanglement. In some cases, parallels can be drawn between the entanglement of photons and the compression of light. For example, you can confuse two beams of light: one squeezed in amplitude, the second in phase.

Quantum cryptography. Stems from quantum entanglement and the picture above. In the simplest quantum cryptography scheme, Alice transmits information to Bob using randomly polarized photons. The direction of compression can play the role of compression: if it is improperly selected, an attacker who intercepts the communication channel will measure noise rather than signal.
Gravitational wave detectors. For this task, you need to catch the smallest fluctuations of huge loads. This is usually done using a Michelson interferometer. It is built very simply: a laser, two mirrors and one translucent plate:

A laser is reflected from two mirrors, two reflections interfere, and an interference pattern forms on the screen. If one of the mirrors moves, then the picture also moves. This happens due to a change in the phase of the wave: the mirror has moved away - the laser path has become a little longer, an additional phase has come in - the interference strips have shifted.
Since the interferometer measures the phase, its resolution cannot be better than the phase uncertainty. For a conventional laser, it is limited to a standard quantum noise level. But if you replace the laser with a phase-squeezed light source, then this problem will disappear, and we will be able to measure distances with unprecedented accuracy.

Today this is done in one of the largest gravitational wave detectors GEO600, and, apparently, is planned for the LISA space detector. By the way, among GT users there is Shkaff , who is just doing this and is ready to answer your questions in the comments.
Accurate phase measurement. Phase-squeezed light can be useful for measurements using the phase contrast method, an everyday technique in modern biology.
How to generate?
Creating compressed light is not so simple. For this, nonlinear optical processes are used. It’s rather difficult to explain on the fingers, but I’ll give one example.
In some crystals, an effect called Kerr nonlinearity is observed - the dependence of the refractive index on the light intensity. Let's send a laser pulse to such a crystal. For any pulse, the intensity at the fronts is lower than in the center — which means that the refractive index will change most strongly where the center of the pulse is now. The difference in refractive indices leads to the fact that the phase of the wave at the center and at the fronts varies differently. The totality of these changes leads to the fact that the phase becomes defined a little better than usual, and the intensity - on the contrary, a little worse. Hello, squeezed light :).
How to detect?
Compressed light can also be measured in several ways.
1. Hanbury Brown-Twiss scheme.

In a series about Hanbury Brown and Twiss, I said that the correlation function g (2) corresponds to the width of the distribution of the number of photons. Amplitude compression of light means that the number of photons is determined better than usual. Therefore, in the broad sense of the word g (2) is less than unity - a sign of squeezed light.
2. Balance detector. This is like the Hanbury Brown-Twiss circuit, but instead of correlations, we either subtract or add signals from two diodes (at our request):

A translucent mirror transmits or reflects each photon randomly. This randomness introduces additional quantum noise (such as shot noise ) into the signal . Such noise has a different sign on two diodes: if a photon is reflected, then it will not fly by; if it flies, it will not be reflected.
If we subtract the signal from one diode from another, then the quantum noise will not go anywhere. And if we add up? Then the noise will disappear, because it has a different sign. (Another explanation: we divided the light into two parts, and then folded them back - this, obviously, did not add additional noise.)
So, subtraction adds us noise with a standard quantum level, and addition does not change anything. If the studied light was amplitude-squeezed (ie, “noiseless”), then subtraction will make it more noisy, and addition will leave it unchanged. Switching between addition and subtraction, we can measure the noise level, and if it is different, then we observe amplitude-squeezed light.

The noise after addition (red) and subtraction (blue) looks something like this. Red noise is much weaker and corresponds to compressed light.
3. Homodyination. Amplitude compression is easy to measure, but what about phase compression? If it is possible to “rotate” the orientation of the ellipse (that is, the phase of light), then the light from the phase-squeezed will become amplitude-squeezed. The phase can be rotated by mixing the light with the reference wave. This is very similar to the receiver-local oscillator, only in the local oscillator the frequency of the reference and studied waves is different, but in the local oscillator it is not (hence the name).
Even in the homodyne, you need to select the phase of the reference wave. In electronics, this is done by a phase shifter, in optics by a delay line (the later the light arrives, the more the phase will run). Mixing takes place on the same translucent mirror:

The reference wave comes from below. And then - the same balanced detector.
And from interesting
So far, compressed light is used only in ultra-precise interferometry. The problem is that it is incredibly fragile. This is easy to understand by the example of ideal amplitude-squeezed light (the photon flux is strictly periodic):

In the propagation of light, losses are inevitable, which are always accidental. This means that the photons will disappear from the stream at random:

As you can see, almost nothing remains of the periodicity. As well as from compression. Therefore, compressed light is very difficult to transmit over long distances.
And finally, let's admire the scheme of the gravitational detector GEO 600 near Hanover:

The source of compressed light is on a yellow background. It uses a nonlinear optical process, but not Kerr nonlinearity, but the generation of the second harmonic of the radiation. The red dotted line is compressed light. Above right is a Michelson interferometer with shoulders of 600 meters; mirrors are suspended on loads that must oscillate from gravitational waves. The picture from the interferometer is obtained on the photodiode in the lower right corner.
Sources of
M. Fox. Quantum optics: An Introduction - Oxford University Press, 2006.
Thanks to Shkaff for the expert comments. Free
images: KDPV , 1 , 2 , 3 , 4 , 5 ,6 , 7 , 8 , 9 , 10 .
